6.2 狭义相对论的基本原理(共27张PPT)
文档属性
| 名称 | 6.2 狭义相对论的基本原理(共27张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 1.0MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 物理 | ||
| 更新时间 | 2020-02-11 00:00:00 | ||
图片预览








文档简介
(共27张PPT)
6.2狭义相对论的基本原理
牛顿力学:宏观……微观(量子力学)
低速……高速(相对论)
……狭义:惯性系,时空与运动
……广义:非惯性系,时空与引力
学习方法: 不要抱住老的时空观念不放,
应该根据实验事实建立新观念。
相对论力学:
一、 牛顿相对性原理(力学相对性原理):
一切力学规律在不同的惯性系中应有相同的形式。
牛顿相对性原理源于牛顿的时空观。
且O? 与 O 重合时,
由时空间隔的绝对性,有:
— 伽利略变换
牛顿的时空观可通过以下坐标和时间变换来体现:
牛顿力学中力和质量都与参考系的选择无关,所以在不同惯性系中 的形式不变。
这表明伽利略变换和力学相对性原理是一致的 。
力学实验无法判定一个惯性系的运动状态
二、经典理论遇到的困难
19世纪下半叶,得到了电磁学的基本规律即麦克斯韦电磁场方程组,不具有伽利略变换下形式不变的特点。
例如,麦克斯韦电磁场方程组中有真空中的电磁波速(光速)c:
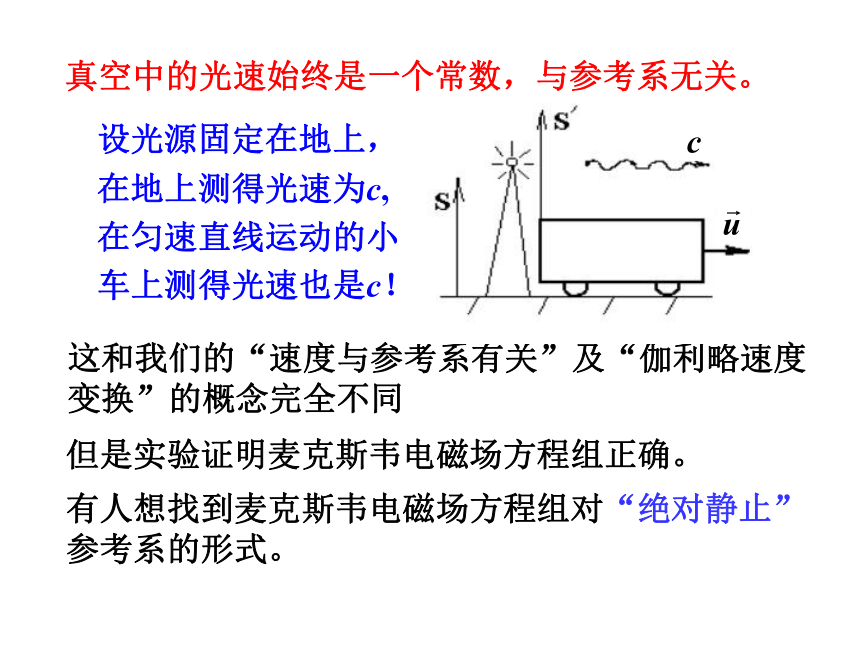
这和我们的“速度与参考系有关”及“伽利略速度变换”的概念完全不同
在地上测得光速为c,
在匀速直线运动的小
车上测得光速也是c!
设光源固定在地上,
真空中的光速始终是一个常数,与参考系无关。
有人想找到麦克斯韦电磁场方程组对“绝对静止”参考系的形式。
但是实验证明麦克斯韦电磁场方程组正确。
企图找到“绝对静止”参考系的实验:
实验目的:干涉仪转90°,观测干涉条纹是否移动?
实验结果:零结果,条纹无移动。以太不存在,光速与参考系无关。
1887年,迈克耳孙─莫雷精确实验却得到“零”结果!
地球就是“绝对静止”的参考系?
有人认为“以太”(ether)是“绝对静止”的参考系,但是以太的性质太不可思议了。 “以太” 不可能存在。种种解释遭到失败。
1922年爱因斯坦在访日的即席演讲中有一段话:
“还在学生时代,我就在想这个问题了。
爱因斯坦认为:物质世界的规律应该是和谐统一的,麦克斯韦方程组应对所有惯性系成立。任何惯性系中光速都是各向为c。
当时,
我知道迈克耳孙实验的奇怪结果。
如果我们承认迈克耳孙的零结果是事实,
球相对以太运动的想法就是错误的。
向狭义相对论的最早的想法。”
我很快得出结论:
这是引导我走
那么地
牛顿的绝对时空观:时间和空间的测量不依顿于惯性参考系而不同。(被认为是天经地义的)
7.2 相对论的基本原理
麦克斯韦方程组并不具有伽利略变换下形式不变的特点。 理论和实验表明光速不变。
(1) 爱因斯坦相对性原理:物理规律对所有惯性
系都是一样的。
(2) 光速不变原理:任何惯性系中,光在真空中
的速率都为c.
爱因斯坦提出狭义相对论的基本原理
意味着伽里略变换应该修改,
意味着牛顿的时空观应该修改 !!!
7.3.1 “同时”的相对性和时间延缓
一. 异地对钟问题
在一个惯性系中, 如何把所有的钟都对同步?
在地球上S系中各处应该配置一系列同步的
静止的钟,来测量S系各处发生的事件的时刻。
注意: 在某惯性系,在某地发生的事件,
应该用该惯性系中该地的钟来计时!
在S’系中各处也应该用一系列同步的静止
的钟,来测量 S’系各处发生的事件的时刻。
7.3 相对论的时空观
二.“同时”的相对性
若两个事件在一个惯性系中看是同时发生的,
在相对运动的另一惯性系中看一般就不是同时了。
……同时的相对性
(不是 A’B’的中点 M’)
S系:按光速不变原理,它们相遇在 AB 的中点 M点。
tA’ > tB’.
S’系:B’处先打
这就是同时的相对性。
关键是光速不变的实验事实!
反过来,如果 S’系中A’、B’同时发生的两个事件,
在 S系中看,也不是同时发生的。
哪处先发生?(两光相会于M’)
答:A处先发生, tA< tB.
关键是什么?
思考
“同时”的相对性说明了时间的量度是相对的。
“时间相差多少”与两个惯性系的
相对运动速度大小有关。
时间的测量是与运动有关的,时间不是绝对的。
tA’ > tB’.
沿垂直于相对运动方向发生的两个件事,
不具有同时的相对性。
设在车厢惯性系S’的A’,B’处各有一个光源,它们同时发出两束光: tA, = tB,
在垂直相对运动的方向上的情况:
沿垂直于相对运动方向发生的
两个事件,不具有同时的相对性。
在地面惯性系 S 中看,两束光是在A、B 两点发出的, AM=BM.所以, t A= tB.
S’系中:光从A’发出又
返回A’的时间间隔为
这是在S’系中同一地点的
同一个钟C’测量的时间。
研究“同时”的相对性的定量关系。
S系中:由于S’系运动,
这两个事件(发光与收到光)
不是发生在同一地点,
所以应由不同地点的C1与C2两个钟测量。
三 . 时间膨胀
光线走的是折线,相应
的时间间隔计算如下:
光速不变
上式解得:
t’……(S’系)同一地点的一个钟测得的两
个事件的时间间隔,称为“原时(原地时)”,
也称为固有时。
△t……(S系)不同地点的两个钟测得的
两个事件的时间间隔,称为“两地时 ( 膨胀时 )”。
因为 u< c , 所以 ? t’即原时(固有时)是最短的!
这就是同样两个事件,在S’系和S系中测得的
时间间隔的关系。
原时最短用钟走的快慢来说:观察者把
相对于他运动的钟和自己的一系列静止的
钟对比,发现那只运动的钟慢了。
比如说,上图中地面上的两地时? t =1秒,
那么车厢上的原时? t’可能是 0.9秒。
即运动的钟走了 0.9秒对应于一系列
静止的钟走了1秒,运动的钟变慢了。
运动时钟变慢,从另一角度来说,就是
运动的钟 0.9秒比静止的钟的 0.9秒要长。
……这称为时间延缓,或钟慢效应。
实际上到底有没有时间延缓效应?
时间延缓早已被高能粒子的许多实验所证实。
若没有时间延缓效应,它们从产生到衰变掉
的时间里,是根本不可能到达地面的实验室的:
我们记 (原时) △t ’= 2×10-6s
因为,它走过的距离只有
u△t’=2.99×108×2×10-6 = 600 m!
这可用时间延缓效应来解释:
在地面参考系S上看,
? -的寿命是两地时,记作△t
它比原时 2×10-6 s 约长16倍!
将运动参考系S’建立在? -上,
按此寿命计算,它在这段时间里,在地面系走的距离为 u△t =2.994×108×3.16×10-5 = 9461 m
(所以能到地面,与实验一致)
我们设想:某人在 u = 0.998c的高速宇宙飞船中渡过
了一天(他是在惯性系中,并没有感到什么不舒服),
那么用地面惯性系中的一系列钟来测量,
同样道理,一定会发现他经历了16天!
实验值:绕地球一周的运动钟变慢 203± 10ns
1971年,美空军用两组Cs(铯)原子钟作实验。
7.3.2 长度收缩
一根棒的长度= 它两个端点的坐标值之差
静止的棒长度的测量 ……静长;
(两端可以不同时测)
运动的棒长度的测量 ……动长。
(两端必须同时测!)
一根棒A’B’静止地放在S’系,固定在 x’轴上。
设在S’系测得
长度为 l’(静长)。
在S系中来测此棒
的长度(动长):
定量分析: 运动的棒长度变了? l 与 l’ 是什么关系?
我们利用原时与两地时的关系来定量计算。
?设在 S 系:
事件1……棒端B’
与x3点重合,
时刻为 t
事件2……棒端A’
与x3点重合,
时刻为 t+△t
两事件的时间间隔
为△t,在S系中是原时。
(这两事件的时间间隔
在S’系中是△t’,是两地时)
在S系中看,棒的
速度 是 u ,所以在
t+△t 时刻,棒端
B’的坐标是
x4 = x3 + u△t
在S系中须同时
测量两端坐标
(都是 t +△t) ,
l = x4 - x3 = u△t
△t = l /u
于是测得动长
△t = ?
设这两个事件的时间间隔为 △t’。
它是 x3 这一点相继
经过 B’和 A’两
点 的时间间隔
( △t’是S’系中
两地时)。
他得到 l ’= u△t’
所以
因为 x3 的速度是 u,
△t = l /u
△t’= l’/u
----(1)
---(2)
?在S’系:
由公式
(原时)(两地时)
l……动长, l’……静长
静长是最长的!
例. 回忆前面 ? - 介子衰变的例子,
用运动长度收缩效应也可以解释:
对? - 介子来说, 地球以
0.998c 的速度向它运动,
9461 m的长度,缩短为
600 m了,所以它能
到达地面实验室。
在某惯性系,在某地发生的事件,
应该用该惯性系中该地的钟来计时!
重要规律:(针对车箱两端打闪的例子)
沿着两个惯性系相对运动方向发
生的两个事件,若在甲惯性系中看是同
时发生的;则在乙惯性系中看就不是
同时发生的,而是在甲惯性系运动的后
方的 那个事件先发生。
沿垂直于相对运动方向发生的
两个事件,不具有同时的相对性。
复习
S系中的测量者必须同时去测量运动棒的
两个端点的坐标。
原时最短用钟走的快慢来说:观察者把
相对于他运动的钟和自己的一系列静止的
钟对比,发现那只运动的钟慢了。
时间膨胀,或钟慢效应:
运动长度收缩效应:
6.2狭义相对论的基本原理
牛顿力学:宏观……微观(量子力学)
低速……高速(相对论)
……狭义:惯性系,时空与运动
……广义:非惯性系,时空与引力
学习方法: 不要抱住老的时空观念不放,
应该根据实验事实建立新观念。
相对论力学:
一、 牛顿相对性原理(力学相对性原理):
一切力学规律在不同的惯性系中应有相同的形式。
牛顿相对性原理源于牛顿的时空观。
且O? 与 O 重合时,
由时空间隔的绝对性,有:
— 伽利略变换
牛顿的时空观可通过以下坐标和时间变换来体现:
牛顿力学中力和质量都与参考系的选择无关,所以在不同惯性系中 的形式不变。
这表明伽利略变换和力学相对性原理是一致的 。
力学实验无法判定一个惯性系的运动状态
二、经典理论遇到的困难
19世纪下半叶,得到了电磁学的基本规律即麦克斯韦电磁场方程组,不具有伽利略变换下形式不变的特点。
例如,麦克斯韦电磁场方程组中有真空中的电磁波速(光速)c:
这和我们的“速度与参考系有关”及“伽利略速度变换”的概念完全不同
在地上测得光速为c,
在匀速直线运动的小
车上测得光速也是c!
设光源固定在地上,
真空中的光速始终是一个常数,与参考系无关。
有人想找到麦克斯韦电磁场方程组对“绝对静止”参考系的形式。
但是实验证明麦克斯韦电磁场方程组正确。
企图找到“绝对静止”参考系的实验:
实验目的:干涉仪转90°,观测干涉条纹是否移动?
实验结果:零结果,条纹无移动。以太不存在,光速与参考系无关。
1887年,迈克耳孙─莫雷精确实验却得到“零”结果!
地球就是“绝对静止”的参考系?
有人认为“以太”(ether)是“绝对静止”的参考系,但是以太的性质太不可思议了。 “以太” 不可能存在。种种解释遭到失败。
1922年爱因斯坦在访日的即席演讲中有一段话:
“还在学生时代,我就在想这个问题了。
爱因斯坦认为:物质世界的规律应该是和谐统一的,麦克斯韦方程组应对所有惯性系成立。任何惯性系中光速都是各向为c。
当时,
我知道迈克耳孙实验的奇怪结果。
如果我们承认迈克耳孙的零结果是事实,
球相对以太运动的想法就是错误的。
向狭义相对论的最早的想法。”
我很快得出结论:
这是引导我走
那么地
牛顿的绝对时空观:时间和空间的测量不依顿于惯性参考系而不同。(被认为是天经地义的)
7.2 相对论的基本原理
麦克斯韦方程组并不具有伽利略变换下形式不变的特点。 理论和实验表明光速不变。
(1) 爱因斯坦相对性原理:物理规律对所有惯性
系都是一样的。
(2) 光速不变原理:任何惯性系中,光在真空中
的速率都为c.
爱因斯坦提出狭义相对论的基本原理
意味着伽里略变换应该修改,
意味着牛顿的时空观应该修改 !!!
7.3.1 “同时”的相对性和时间延缓
一. 异地对钟问题
在一个惯性系中, 如何把所有的钟都对同步?
在地球上S系中各处应该配置一系列同步的
静止的钟,来测量S系各处发生的事件的时刻。
注意: 在某惯性系,在某地发生的事件,
应该用该惯性系中该地的钟来计时!
在S’系中各处也应该用一系列同步的静止
的钟,来测量 S’系各处发生的事件的时刻。
7.3 相对论的时空观
二.“同时”的相对性
若两个事件在一个惯性系中看是同时发生的,
在相对运动的另一惯性系中看一般就不是同时了。
……同时的相对性
(不是 A’B’的中点 M’)
S系:按光速不变原理,它们相遇在 AB 的中点 M点。
tA’ > tB’.
S’系:B’处先打
这就是同时的相对性。
关键是光速不变的实验事实!
反过来,如果 S’系中A’、B’同时发生的两个事件,
在 S系中看,也不是同时发生的。
哪处先发生?(两光相会于M’)
答:A处先发生, tA< tB.
关键是什么?
思考
“同时”的相对性说明了时间的量度是相对的。
“时间相差多少”与两个惯性系的
相对运动速度大小有关。
时间的测量是与运动有关的,时间不是绝对的。
tA’ > tB’.
沿垂直于相对运动方向发生的两个件事,
不具有同时的相对性。
设在车厢惯性系S’的A’,B’处各有一个光源,它们同时发出两束光: tA, = tB,
在垂直相对运动的方向上的情况:
沿垂直于相对运动方向发生的
两个事件,不具有同时的相对性。
在地面惯性系 S 中看,两束光是在A、B 两点发出的, AM=BM.所以, t A= tB.
S’系中:光从A’发出又
返回A’的时间间隔为
这是在S’系中同一地点的
同一个钟C’测量的时间。
研究“同时”的相对性的定量关系。
S系中:由于S’系运动,
这两个事件(发光与收到光)
不是发生在同一地点,
所以应由不同地点的C1与C2两个钟测量。
三 . 时间膨胀
光线走的是折线,相应
的时间间隔计算如下:
光速不变
上式解得:
t’……(S’系)同一地点的一个钟测得的两
个事件的时间间隔,称为“原时(原地时)”,
也称为固有时。
△t……(S系)不同地点的两个钟测得的
两个事件的时间间隔,称为“两地时 ( 膨胀时 )”。
因为 u< c , 所以 ? t’即原时(固有时)是最短的!
这就是同样两个事件,在S’系和S系中测得的
时间间隔的关系。
原时最短用钟走的快慢来说:观察者把
相对于他运动的钟和自己的一系列静止的
钟对比,发现那只运动的钟慢了。
比如说,上图中地面上的两地时? t =1秒,
那么车厢上的原时? t’可能是 0.9秒。
即运动的钟走了 0.9秒对应于一系列
静止的钟走了1秒,运动的钟变慢了。
运动时钟变慢,从另一角度来说,就是
运动的钟 0.9秒比静止的钟的 0.9秒要长。
……这称为时间延缓,或钟慢效应。
实际上到底有没有时间延缓效应?
时间延缓早已被高能粒子的许多实验所证实。
若没有时间延缓效应,它们从产生到衰变掉
的时间里,是根本不可能到达地面的实验室的:
我们记 (原时) △t ’= 2×10-6s
因为,它走过的距离只有
u△t’=2.99×108×2×10-6 = 600 m!
这可用时间延缓效应来解释:
在地面参考系S上看,
? -的寿命是两地时,记作△t
它比原时 2×10-6 s 约长16倍!
将运动参考系S’建立在? -上,
按此寿命计算,它在这段时间里,在地面系走的距离为 u△t =2.994×108×3.16×10-5 = 9461 m
(所以能到地面,与实验一致)
我们设想:某人在 u = 0.998c的高速宇宙飞船中渡过
了一天(他是在惯性系中,并没有感到什么不舒服),
那么用地面惯性系中的一系列钟来测量,
同样道理,一定会发现他经历了16天!
实验值:绕地球一周的运动钟变慢 203± 10ns
1971年,美空军用两组Cs(铯)原子钟作实验。
7.3.2 长度收缩
一根棒的长度= 它两个端点的坐标值之差
静止的棒长度的测量 ……静长;
(两端可以不同时测)
运动的棒长度的测量 ……动长。
(两端必须同时测!)
一根棒A’B’静止地放在S’系,固定在 x’轴上。
设在S’系测得
长度为 l’(静长)。
在S系中来测此棒
的长度(动长):
定量分析: 运动的棒长度变了? l 与 l’ 是什么关系?
我们利用原时与两地时的关系来定量计算。
?设在 S 系:
事件1……棒端B’
与x3点重合,
时刻为 t
事件2……棒端A’
与x3点重合,
时刻为 t+△t
两事件的时间间隔
为△t,在S系中是原时。
(这两事件的时间间隔
在S’系中是△t’,是两地时)
在S系中看,棒的
速度 是 u ,所以在
t+△t 时刻,棒端
B’的坐标是
x4 = x3 + u△t
在S系中须同时
测量两端坐标
(都是 t +△t) ,
l = x4 - x3 = u△t
△t = l /u
于是测得动长
△t = ?
设这两个事件的时间间隔为 △t’。
它是 x3 这一点相继
经过 B’和 A’两
点 的时间间隔
( △t’是S’系中
两地时)。
他得到 l ’= u△t’
所以
因为 x3 的速度是 u,
△t = l /u
△t’= l’/u
----(1)
---(2)
?在S’系:
由公式
(原时)(两地时)
l……动长, l’……静长
静长是最长的!
例. 回忆前面 ? - 介子衰变的例子,
用运动长度收缩效应也可以解释:
对? - 介子来说, 地球以
0.998c 的速度向它运动,
9461 m的长度,缩短为
600 m了,所以它能
到达地面实验室。
在某惯性系,在某地发生的事件,
应该用该惯性系中该地的钟来计时!
重要规律:(针对车箱两端打闪的例子)
沿着两个惯性系相对运动方向发
生的两个事件,若在甲惯性系中看是同
时发生的;则在乙惯性系中看就不是
同时发生的,而是在甲惯性系运动的后
方的 那个事件先发生。
沿垂直于相对运动方向发生的
两个事件,不具有同时的相对性。
复习
S系中的测量者必须同时去测量运动棒的
两个端点的坐标。
原时最短用钟走的快慢来说:观察者把
相对于他运动的钟和自己的一系列静止的
钟对比,发现那只运动的钟慢了。
时间膨胀,或钟慢效应:
运动长度收缩效应:
同课章节目录
- 第一章 怎样研究抛体运动
- 1 飞机投弹与平抛运动
- 2 研究平抛运动的规律
- 3 研究斜抛运动
- 第二章 研究圆周运动
- 1 怎样描述圆周运动
- 2 研究匀速圆周运动的规律
- 3 圆周运动的案例分析
- 4 研究离心现象及其应用
- 第三章 动能的变化与机械功
- 1 探究动能变化跟功的关系
- 2 研究功与功率
- 3 动能定理的应用
- 第四章 能量守恒与可持续发展
- 1 势能的变化与机械功
- 2 研究机械能守恒定律
- 3 能量的转化与守恒
- 4 能源与可持续发展
- 第五章 万有引力与航天
- 1 从托勒密到开普勒
- 2 万有引力定律是怎样发现的
- 3 万有引力定律与天文学的新发现
- 4 飞出地球去
- 第六章 经典力学与现代物理
- 1 经典力学的巨大成就和局限性
- 2 狭义相对论的基本原理
- 3 爱因斯坦心目中的宇宙
- 4 微观世界与量子论
