第6课时 解决实际问题 (共15张PPT)
文档属性
| 名称 | 第6课时 解决实际问题 (共15张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 2.3MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-02-11 00:00:00 | ||
图片预览



文档简介
课件15张PPT。解决实际问题人教版数学六年级上册 第五单元
12.56÷3.14÷2=2(cm)1. 一个圆的周长是12.56 cm,求它的半径。2. 一个圆形茶几面的半径是3 dm ,它的面积是多少平方分米?3.14×32=28.26(dm2)3.右图是一个标准的半圆,它的直径是5 cm。你能算出它的面积和周长吗?
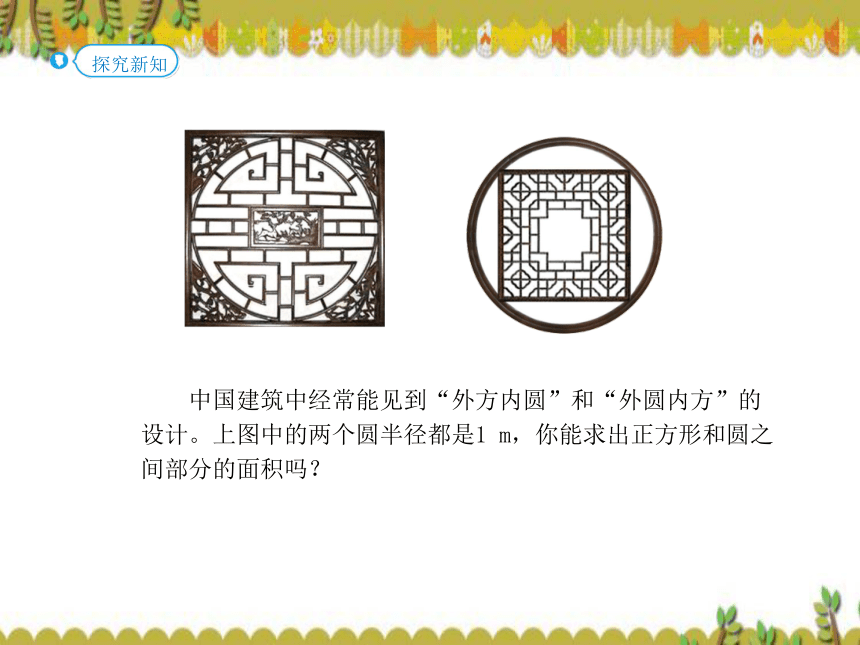
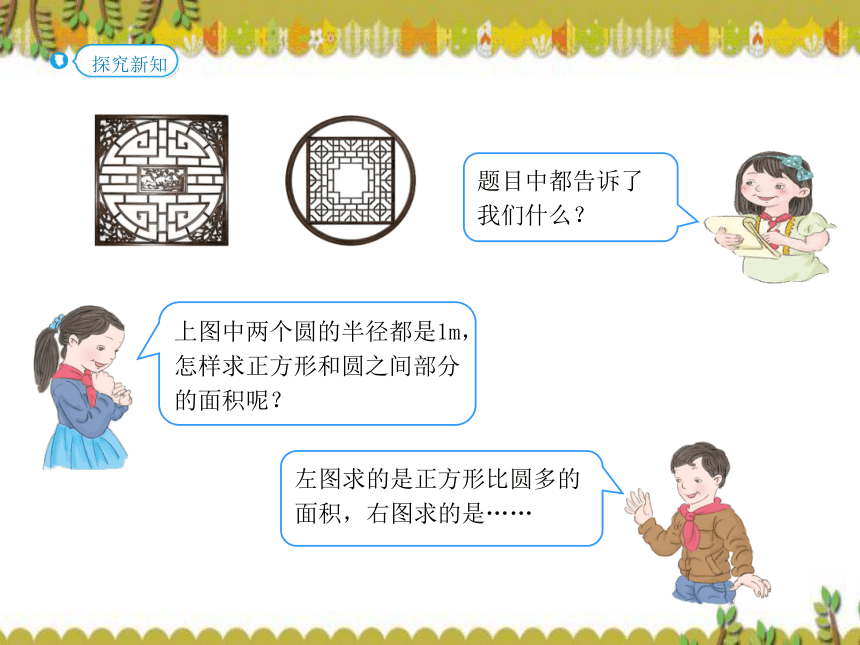
3.右图是一个标准的半圆,它的直径是5 cm。你能算出它的面积和周长吗?(1)半圆是什么意思?如何求这个半圆的面积?半圆就是圆的一半,可以先求出整个圆的面积再除以2,
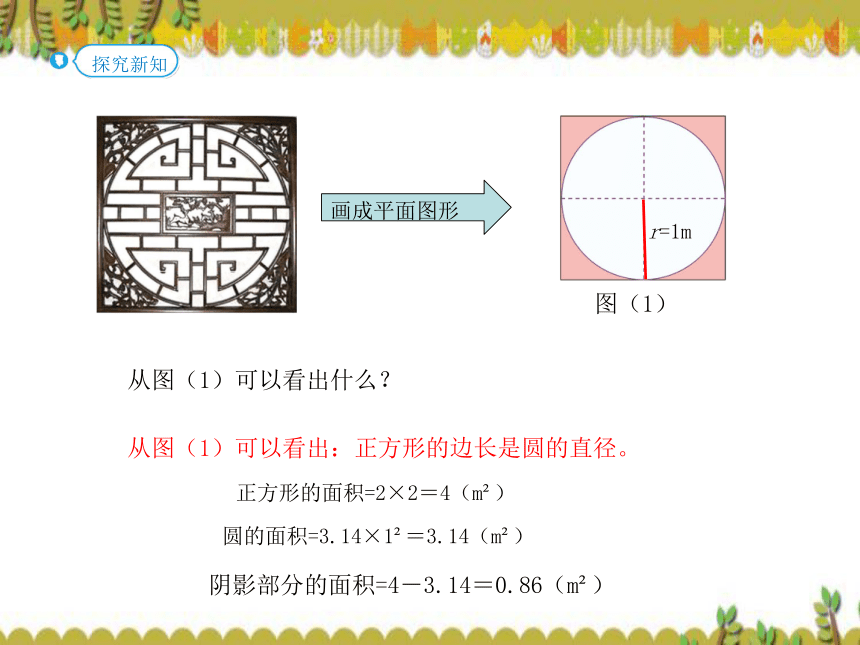
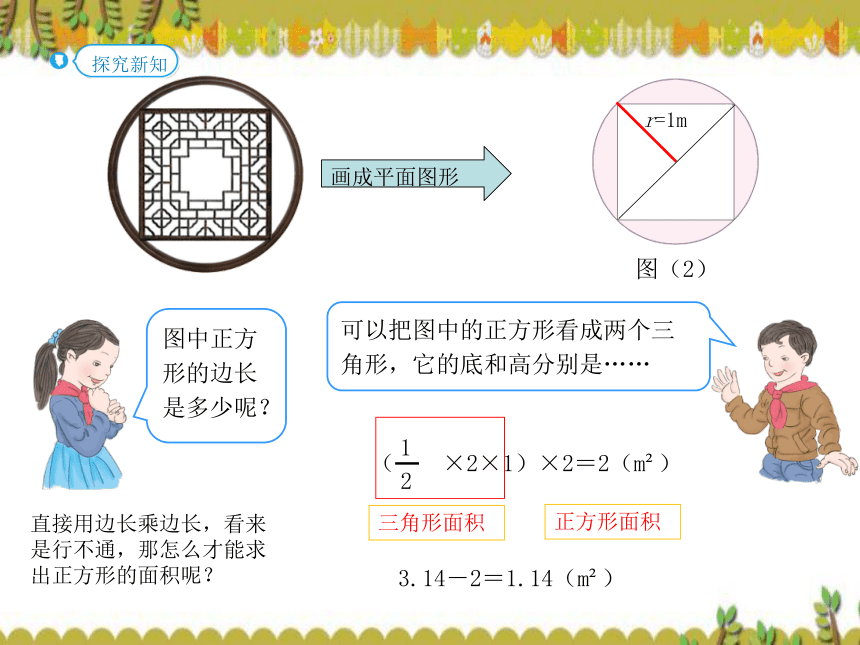
就能算出这个半圆的面积。S=πr2 =3.14×(5÷2)2 =3.14×2.52 =19.625( cm2)(2)半圆的周长怎么求,是不是这个圆的周长的一半? 不是,圆的周长的一半,还要加上一条直径。C=πd=3.14×5=15.7(cm)半圆周长=15.7÷2+5=12.85(cm) 中国建筑中经常能见到“外方内圆”和“外圆内方”的设计。上图中的两个圆半径都是1 m,你能求出正方形和圆之间部分的面积吗?从图(1)可以看出什么?阴影部分的面积=4-3.14=0.86(m2)圆的面积=3.14×12=3.14(m2)画成平面图形正方形的面积=2×2=4(m2)从图(1)可以看出:正方形的边长是圆的直径。3.14-2=1.14(m2)画成平面图形三角形面积正方形面积直接用边长乘边长,看来是行不通,那怎么才能求出正方形的面积呢?
提醒:我们在用这两个公式时,必须先写出推导过程,再代入数字计算才算正确。 正方形面积= 2r×2r=4 r2
圆的面积=πr2
正方形面积-圆的面积
=4r2-πr2=(4- π ) r2 =0.86 r2
外方接内圆:
外圆接内方:
圆的面积=πr2
正方形面积= 2r×r÷2×2= 2r2
正方形面积-圆的面积
=πr2-2r2 =( π -2)
r2=1.14r2
右图是一面我国唐代外圆内方的铜镜。铜镜的直径是24.8 cm。外面的圆与内部的正方形
之间的面积是多少?答:外面的圆与内部的正方形之间的面积约是175.28 cm2 。3.14×(24.8÷2)2=482.8064 ≈482.8(cm2)
24.8×(24.8÷2)÷2×2=307.52(cm2)
482.8-307.52=175.28(cm2)
用普通方法计算: 右图是一面我国唐代外圆内方的铜镜。铜镜的直径是24.8 cm。外面的圆与内部的正方形
之间的面积是多少?答:外面的圆与内部的正方形之间的面积约是175.29 cm2 。用刚才所学的特殊办法计算:圆的面积= π r2
正方形面积= 2r×r÷2×2=2r2
正方形面积-圆的面积= π r2-2r2 =( π -2) r2=1.14r2
d=24.8
1.14× 12.42 ≈175.29 (cm2)
r=12.4
这是一个外方接内圆图形,正方形的边长是20 cm,求正方形和圆之间的面积。方法一:正方形面积:?圆的面积:?之间面积:?方法二:正方形面积= 2r×2r=4 r2
圆的面积=πr2
正方形面积-圆的面积=4r2-πr2=(4- π ) r2 =0.86 r2
d=20
r=10
0.86×102=86(cm2)
这个古钱币的直径是5 cm,里面的正方形的边长是1cm,这个古钱币的面积是多少?假如这个钱币中间空的部分是一个周长为9.42 cm的圆,那么这个钱币的面积又是多少呢?正方形面积:圆的面积:钱币面积:这个题目和前面学过的外圆接内方一样吗?3.14×(5÷2)2=19.625(cm2)
1×1=1(cm2)
19.625-1=18.625(cm2)
这个古钱币的直径是5 cm,里面的正方形边长是1 cm,这个古钱币的面积是多少?假如这个钱币中间空的部分是一个周长为9.42 m的圆,那么这个钱币的面积又是多少呢?小圆面积:9.42÷3.14÷2=1.5(cm)大圆面积:钱币面积:?0003.14×(5÷2)2=19.625(cm2)
19.625-7.065=12.56(cm2)
大脸猫和蓝皮鼠都认为自己跑得快。 大脸猫说:“我腿长,步子大,一步顶你两步,我跑得一定比你快!” 蓝皮鼠不甘示弱地说:“我虽然腿短,但是步子迈得快,你刚迈出一步,我三步都迈出去了,我跑得肯定比你快!” 它们两个争论半天,谁也不服气,只好实地比试一下。刚好一个工地上画了三个半圆(一个大的半圆,两个小的半圆;已知大的半圆的直径是小的半圆的直径的2倍)。 大脸猫指着半圆说:“沿着这个大半圆可以从甲处跑到乙处,沿着这两个小的半圆也可以从甲处跑到乙处。两条道路你挑吧。”蓝皮鼠挑选了两个小半圆连接成的道路。 他们两个在甲处站好,一声令下,各自沿着自己选择的道路飞快地跑着。大脸猫腿长步大,蓝皮鼠步小轻快。说也奇怪,他们两个不先不后同时到达了乙处。他们尽管谁也不服气,可是谁也说不出什么来。 这两条道路哪个长呢?其实是一样长。 如果把两个小半圆改成三个小半圆、四个小半圆……一百个小半圆呢,大半圆的周长和这些小半圆的周长之和仍然相等吗?回答是肯定的。从计算圆周长的公式上很容易看到这个结论,不信你就动手算算。 大脸猫和蓝皮鼠赛跑
12.56÷3.14÷2=2(cm)1. 一个圆的周长是12.56 cm,求它的半径。2. 一个圆形茶几面的半径是3 dm ,它的面积是多少平方分米?3.14×32=28.26(dm2)3.右图是一个标准的半圆,它的直径是5 cm。你能算出它的面积和周长吗?
3.右图是一个标准的半圆,它的直径是5 cm。你能算出它的面积和周长吗?(1)半圆是什么意思?如何求这个半圆的面积?半圆就是圆的一半,可以先求出整个圆的面积再除以2,
就能算出这个半圆的面积。S=πr2 =3.14×(5÷2)2 =3.14×2.52 =19.625( cm2)(2)半圆的周长怎么求,是不是这个圆的周长的一半? 不是,圆的周长的一半,还要加上一条直径。C=πd=3.14×5=15.7(cm)半圆周长=15.7÷2+5=12.85(cm) 中国建筑中经常能见到“外方内圆”和“外圆内方”的设计。上图中的两个圆半径都是1 m,你能求出正方形和圆之间部分的面积吗?从图(1)可以看出什么?阴影部分的面积=4-3.14=0.86(m2)圆的面积=3.14×12=3.14(m2)画成平面图形正方形的面积=2×2=4(m2)从图(1)可以看出:正方形的边长是圆的直径。3.14-2=1.14(m2)画成平面图形三角形面积正方形面积直接用边长乘边长,看来是行不通,那怎么才能求出正方形的面积呢?
提醒:我们在用这两个公式时,必须先写出推导过程,再代入数字计算才算正确。 正方形面积= 2r×2r=4 r2
圆的面积=πr2
正方形面积-圆的面积
=4r2-πr2=(4- π ) r2 =0.86 r2
外方接内圆:
外圆接内方:
圆的面积=πr2
正方形面积= 2r×r÷2×2= 2r2
正方形面积-圆的面积
=πr2-2r2 =( π -2)
r2=1.14r2
右图是一面我国唐代外圆内方的铜镜。铜镜的直径是24.8 cm。外面的圆与内部的正方形
之间的面积是多少?答:外面的圆与内部的正方形之间的面积约是175.28 cm2 。3.14×(24.8÷2)2=482.8064 ≈482.8(cm2)
24.8×(24.8÷2)÷2×2=307.52(cm2)
482.8-307.52=175.28(cm2)
用普通方法计算: 右图是一面我国唐代外圆内方的铜镜。铜镜的直径是24.8 cm。外面的圆与内部的正方形
之间的面积是多少?答:外面的圆与内部的正方形之间的面积约是175.29 cm2 。用刚才所学的特殊办法计算:圆的面积= π r2
正方形面积= 2r×r÷2×2=2r2
正方形面积-圆的面积= π r2-2r2 =( π -2) r2=1.14r2
d=24.8
1.14× 12.42 ≈175.29 (cm2)
r=12.4
这是一个外方接内圆图形,正方形的边长是20 cm,求正方形和圆之间的面积。方法一:正方形面积:?圆的面积:?之间面积:?方法二:正方形面积= 2r×2r=4 r2
圆的面积=πr2
正方形面积-圆的面积=4r2-πr2=(4- π ) r2 =0.86 r2
d=20
r=10
0.86×102=86(cm2)
这个古钱币的直径是5 cm,里面的正方形的边长是1cm,这个古钱币的面积是多少?假如这个钱币中间空的部分是一个周长为9.42 cm的圆,那么这个钱币的面积又是多少呢?正方形面积:圆的面积:钱币面积:这个题目和前面学过的外圆接内方一样吗?3.14×(5÷2)2=19.625(cm2)
1×1=1(cm2)
19.625-1=18.625(cm2)
这个古钱币的直径是5 cm,里面的正方形边长是1 cm,这个古钱币的面积是多少?假如这个钱币中间空的部分是一个周长为9.42 m的圆,那么这个钱币的面积又是多少呢?小圆面积:9.42÷3.14÷2=1.5(cm)大圆面积:钱币面积:?0003.14×(5÷2)2=19.625(cm2)
19.625-7.065=12.56(cm2)
大脸猫和蓝皮鼠都认为自己跑得快。 大脸猫说:“我腿长,步子大,一步顶你两步,我跑得一定比你快!” 蓝皮鼠不甘示弱地说:“我虽然腿短,但是步子迈得快,你刚迈出一步,我三步都迈出去了,我跑得肯定比你快!” 它们两个争论半天,谁也不服气,只好实地比试一下。刚好一个工地上画了三个半圆(一个大的半圆,两个小的半圆;已知大的半圆的直径是小的半圆的直径的2倍)。 大脸猫指着半圆说:“沿着这个大半圆可以从甲处跑到乙处,沿着这两个小的半圆也可以从甲处跑到乙处。两条道路你挑吧。”蓝皮鼠挑选了两个小半圆连接成的道路。 他们两个在甲处站好,一声令下,各自沿着自己选择的道路飞快地跑着。大脸猫腿长步大,蓝皮鼠步小轻快。说也奇怪,他们两个不先不后同时到达了乙处。他们尽管谁也不服气,可是谁也说不出什么来。 这两条道路哪个长呢?其实是一样长。 如果把两个小半圆改成三个小半圆、四个小半圆……一百个小半圆呢,大半圆的周长和这些小半圆的周长之和仍然相等吗?回答是肯定的。从计算圆周长的公式上很容易看到这个结论,不信你就动手算算。 大脸猫和蓝皮鼠赛跑
