五年级上册数学试题-6《多边形的面积》专项培优 人教新课标含答案
文档属性
| 名称 | 五年级上册数学试题-6《多边形的面积》专项培优 人教新课标含答案 |  | |
| 格式 | zip | ||
| 文件大小 | 1.6MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-02-12 16:31:12 | ||
图片预览


文档简介
《多边形的面积》专项培优
专项一运用等分法巧求面积
例1 如图是两个完全一样的等腰直角三角形,图①中正方形的面积是40平方分米,则图②中正方形的面积是多少平方分米?
分析 等分法,就是将整个图形平均分成若干份,再看所求图形的面积占多少份,从而求出所要求的图形面积。
本题中,根据图①中正方形的面积与大等腰直角三角形的面积关系,可求出大等腰直角三角形的面积;然后根据图②中正方形的面积与大等腰直角三角形的面积关系,求出图②中正方形的面积。
解答 如图,运用等分法把图①平均分成9份,正方形的面积相当于这样的4份;把图②平均分成4份,正方形的面积相当于这样的2份。等腰直角三角形的面积为40÷4×9=90(平方分米),图②中正方形的面积为90÷2=45(平方分米)。
反馈练习
1.如图,七巧板拼成的正方形边长是20厘米,求图中阴影部分的面积
2.如图,在一个面积是36平方分米的大正方形中,有两个带阴影的小正方形。求阴影部分的面积和。
3.如图,将等腰直角三角形ABC与等腰直角三角形DEC重叠在一起,阴影部分是一个正方形。已知三角形ABC的面积是72平方厘米,求三角形DEC的面积。
专项二运用等积变换巧求面积
例2 如图,已知长方形ABCD的面积是1200平方厘米,阴影部分的面积是750平方厘米,求四边形EFGO的面积。
分析 根据图形特点,由面积与面积之间的相等关系,进行一些转化,从而使间题得到简便解决。本题根据题目中图形之间面积相等的关系可以将上图中的阴影部分三角形ABE移至三角形DFE中,从而求出四边形EFGO的面积。
解答 在长方形ABCD中,三角形ABF与三角形DBF同底(即BF的长)、等高(即长方形的宽),所以三角形ABF与三角形DBF的面积相等。若从这两个三角形中同时减去三角形BEF则剩下的图形面积相等,即:三角形ABE与三角形DFE的面积相等。这样阴影部分的面积就等于四边形EFCO加上三角形ACD的面积,要求四边形EFGO的面积,只要用阴影部分的面积减去三角形ACD的面积,列式为750-1200÷2=150(平方厘米)。
反馈练习
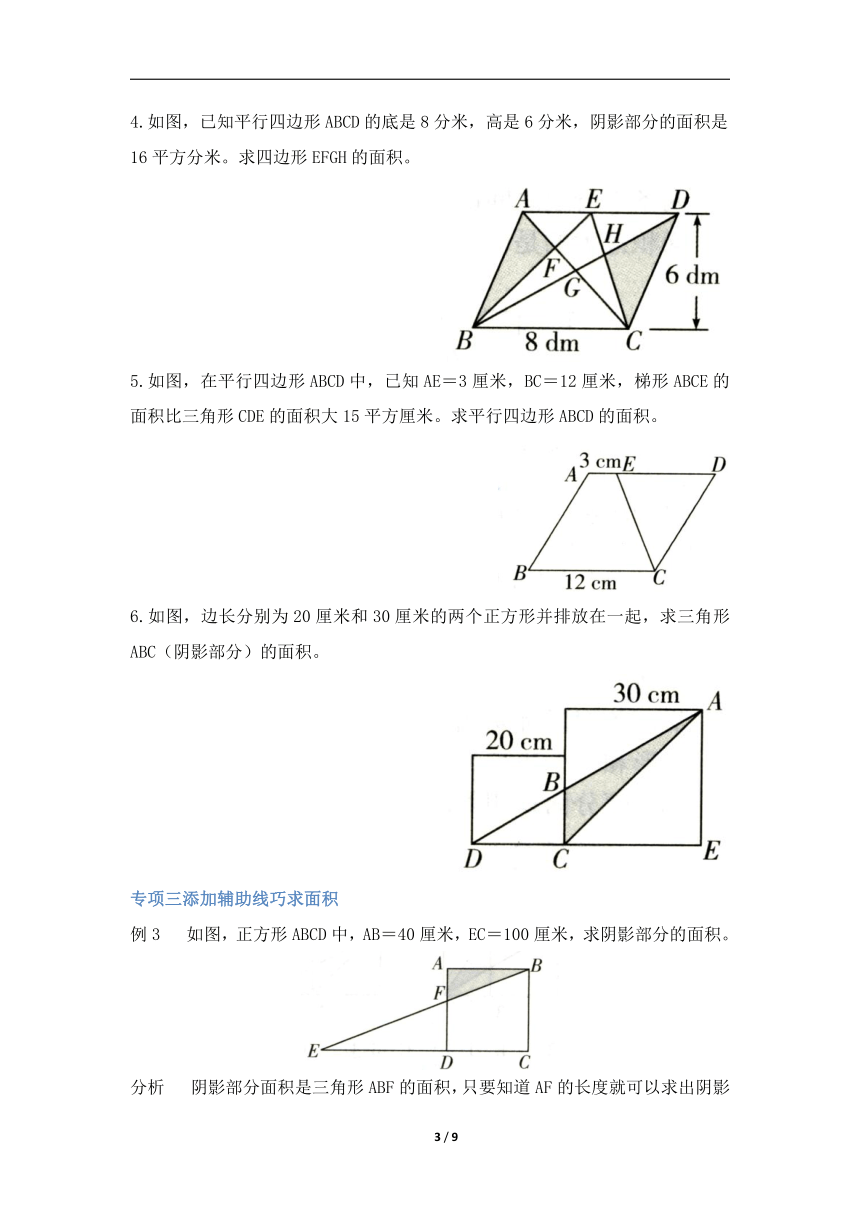
4.如图,已知平行四边形ABCD的底是8分米,高是6分米,阴影部分的面积是16平方分米。求四边形EFGH的面积。
5.如图,在平行四边形ABCD中,已知AE=3厘米,BC=12厘米,梯形ABCE的面积比三角形CDE的面积大15平方厘米。求平行四边形ABCD的面积。
6.如图,边长分别为20厘米和30厘米的两个正方形并排放在一起,求三角形ABC(阴影部分)的面积。
专项三添加辅助线巧求面积
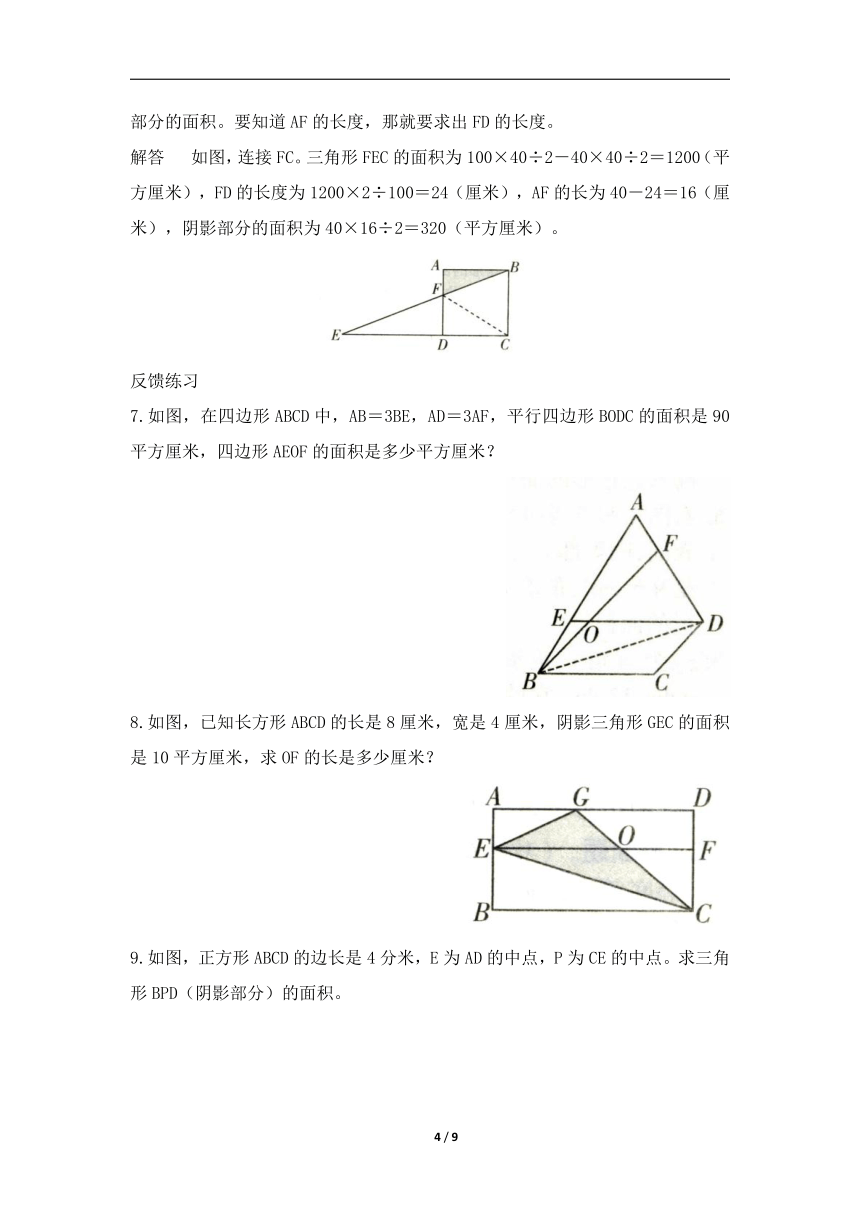
例3 如图,正方形ABCD中,AB=40厘米,EC=100厘米,求阴影部分的面积。
分析 阴影部分面积是三角形ABF的面积,只要知道AF的长度就可以求出阴影部分的面积。要知道AF的长度,那就要求出FD的长度。
解答 如图,连接FC。三角形FEC的面积为100×40÷2-40×40÷2=1200(平方厘米),FD的长度为1200×2÷100=24(厘米),AF的长为40-24=16(厘米),阴影部分的面积为40×16÷2=320(平方厘米)。
反馈练习
7.如图,在四边形ABCD中,AB=3BE,AD=3AF,平行四边形BODC的面积是90平方厘米,四边形AEOF的面积是多少平方厘米?
8.如图,已知长方形ABCD的长是8厘米,宽是4厘米,阴影三角形GEC的面积是10平方厘米,求OF的长是多少厘米?
9.如图,正方形ABCD的边长是4分米,E为AD的中点,P为CE的中点。求三角形BPD(阴影部分)的面积。
参考答案:
1.20×20÷16×2=50(平方厘米) 提示:如图分成16份,阴影部分是这样的2份。
2.36÷2=18(平方分米) 18÷2+18÷9×4=17(平方分米) 提示:如图,通过等分可以发现,左下角的阴影正方形占所在三角形面积的一半,右上角的阴影正方形占所在三角形面积的。分别求出两个三角形的面积,再求阴影部分的面积和。
3.72÷9×8=64(平方厘米) 提示:如图,通过等分可以发现,三角
形ABC被平均分成了9份,三角形DEC被平均分成了8份。由于两个三角形中每一份的大小相同,所以要求三角形DEC的面积,需先求出一份的面积。
4.16-8×6÷4=4(平方分米) 提示:三角形BAE与三角形CAE等底等高,则它们的面积相等。从这两个三角形中同时减去三角形AEF,则剩下的面积相等,即三角形ABF与三角形CEF的面积相等。要求四边形EFGH的面积,就相当于用图中阴影部分的面积减去三角形DGC的面积。
5.15÷3=5(厘米) 12×5=60(平方厘米) 提示:过E点作CD的平行线,交BC于点F(如图),由此可看出,平行四边形ABFE的面积就是题中梯形与三角形的面积差,也就是15平方厘米。因为平行四边形ABFE的底AE长3厘米,所以它的高,也就是平行四边形ABCD的高就是15÷3=5(厘米)。因此,平行四边形ABCD的面积是12×5=60(平方厘米)。
6.20×30÷2=300(平方厘米) 300×2÷(20+30)=12(厘米) 12×30÷2=180(平方厘米) 提示:如图连接BE。观察发现,三角形ABC与三角形EBC等底等高,则它们的面积相等。由此可推出,S△ABC +S△BDC=S△EBC+S△BDC,即S△ADC=S△EBD。三角形ADC(三角形EDB)的面积为20×30÷2=300(平方厘米),BC的长为300×2÷(20+30)=12(厘米),三角形ABC的面积为12×30÷2=180(平方厘米)。
7.90÷2=45(平方厘米) 提示:从题图中可以看出角形ABF与三角形ABD的高相等,AD=3AF,则形ABD的面积是三角形ABF面积的3倍;同理可得,三角形ABD的面积是三角形BDE面积的3倍。由此可以推出,三角形ABF与三角形BDE的面积相等。若从这两个三角形中同时减去三角形BOE,则剩下的图形面积相等,即:四边形AEOF与三角形BOD的面积相等。因为三角形BOD的面积是平行四边BODC面积的一半,所以四边形AEOF的面积也是行四边形BODC面积的一半。故四边形AEOF的面积为90÷2=45(平方厘米)。
8.方法一:8-10×2÷4=3(厘米) 提示:如图,连接OA、OB。观察发现,三角形AEO与三角形GEO等底高,则它们的面积相等:同理,三角形BEO与三角CEO的面积相等。由此可推出,S△AEO+S△BEO=S△GEO+S△CEO,S△AOB=S阴影△GEC。根据三角形
AOB面积是10平方厘米,底AB的长是4厘米,可求出OE的长为10×2÷4=5(厘米)。然后用EF的长减OE的长,就可以求出OF的长为8-5=3(厘米)。
方法二:8×4÷2-10=6(平方厘米) 6×2÷4=3(厘米) 提示:如图,连接DE、DO观察发现,三角GEO与三角形DEO等底等高,则它们的面积相等。用三角形ECD的面积减去阴影部分的面积,就可求出三角形OCD的面积为8×4÷2-10=6(平方厘米)。三角形OCD的底CD的长为4厘米,则它的高OF的长为6×2÷4=3(厘米)。
9.4×4÷2=8(平方分米) (4÷2)×4÷2=4(平方分米)
8-8÷2-4÷2=2(平方分米) 提示:如图,连接BE。观察发现三角形EBC、三角形DBC都与形ABCD等底等高,它们的面积都是正方形ABCD面积的一半,面积为4×4÷2=8(平方分米)。由于E为AD的中点,则三角形DEC的面积为(4+2)×4÷2=4(平方分米)。由于P为CE的中点,则三角形DEP与三角DCP等底等高,面积相等,三角形DCP的面积相当于三角形DEC面积的一半,面积为4÷2=2(平方分米);同理,三角形BCP的面积为8÷2=4(平方分米)。
要求三角形BPD(阴影部分)的面积,只需用三角形DBC的面积分别减去三角形BCP的面积和三角形DCP的面积,列式为8-4-2=2(平方分米)。
专项一运用等分法巧求面积
例1 如图是两个完全一样的等腰直角三角形,图①中正方形的面积是40平方分米,则图②中正方形的面积是多少平方分米?
分析 等分法,就是将整个图形平均分成若干份,再看所求图形的面积占多少份,从而求出所要求的图形面积。
本题中,根据图①中正方形的面积与大等腰直角三角形的面积关系,可求出大等腰直角三角形的面积;然后根据图②中正方形的面积与大等腰直角三角形的面积关系,求出图②中正方形的面积。
解答 如图,运用等分法把图①平均分成9份,正方形的面积相当于这样的4份;把图②平均分成4份,正方形的面积相当于这样的2份。等腰直角三角形的面积为40÷4×9=90(平方分米),图②中正方形的面积为90÷2=45(平方分米)。
反馈练习
1.如图,七巧板拼成的正方形边长是20厘米,求图中阴影部分的面积
2.如图,在一个面积是36平方分米的大正方形中,有两个带阴影的小正方形。求阴影部分的面积和。
3.如图,将等腰直角三角形ABC与等腰直角三角形DEC重叠在一起,阴影部分是一个正方形。已知三角形ABC的面积是72平方厘米,求三角形DEC的面积。
专项二运用等积变换巧求面积
例2 如图,已知长方形ABCD的面积是1200平方厘米,阴影部分的面积是750平方厘米,求四边形EFGO的面积。
分析 根据图形特点,由面积与面积之间的相等关系,进行一些转化,从而使间题得到简便解决。本题根据题目中图形之间面积相等的关系可以将上图中的阴影部分三角形ABE移至三角形DFE中,从而求出四边形EFGO的面积。
解答 在长方形ABCD中,三角形ABF与三角形DBF同底(即BF的长)、等高(即长方形的宽),所以三角形ABF与三角形DBF的面积相等。若从这两个三角形中同时减去三角形BEF则剩下的图形面积相等,即:三角形ABE与三角形DFE的面积相等。这样阴影部分的面积就等于四边形EFCO加上三角形ACD的面积,要求四边形EFGO的面积,只要用阴影部分的面积减去三角形ACD的面积,列式为750-1200÷2=150(平方厘米)。
反馈练习
4.如图,已知平行四边形ABCD的底是8分米,高是6分米,阴影部分的面积是16平方分米。求四边形EFGH的面积。
5.如图,在平行四边形ABCD中,已知AE=3厘米,BC=12厘米,梯形ABCE的面积比三角形CDE的面积大15平方厘米。求平行四边形ABCD的面积。
6.如图,边长分别为20厘米和30厘米的两个正方形并排放在一起,求三角形ABC(阴影部分)的面积。
专项三添加辅助线巧求面积
例3 如图,正方形ABCD中,AB=40厘米,EC=100厘米,求阴影部分的面积。
分析 阴影部分面积是三角形ABF的面积,只要知道AF的长度就可以求出阴影部分的面积。要知道AF的长度,那就要求出FD的长度。
解答 如图,连接FC。三角形FEC的面积为100×40÷2-40×40÷2=1200(平方厘米),FD的长度为1200×2÷100=24(厘米),AF的长为40-24=16(厘米),阴影部分的面积为40×16÷2=320(平方厘米)。
反馈练习
7.如图,在四边形ABCD中,AB=3BE,AD=3AF,平行四边形BODC的面积是90平方厘米,四边形AEOF的面积是多少平方厘米?
8.如图,已知长方形ABCD的长是8厘米,宽是4厘米,阴影三角形GEC的面积是10平方厘米,求OF的长是多少厘米?
9.如图,正方形ABCD的边长是4分米,E为AD的中点,P为CE的中点。求三角形BPD(阴影部分)的面积。
参考答案:
1.20×20÷16×2=50(平方厘米) 提示:如图分成16份,阴影部分是这样的2份。
2.36÷2=18(平方分米) 18÷2+18÷9×4=17(平方分米) 提示:如图,通过等分可以发现,左下角的阴影正方形占所在三角形面积的一半,右上角的阴影正方形占所在三角形面积的。分别求出两个三角形的面积,再求阴影部分的面积和。
3.72÷9×8=64(平方厘米) 提示:如图,通过等分可以发现,三角
形ABC被平均分成了9份,三角形DEC被平均分成了8份。由于两个三角形中每一份的大小相同,所以要求三角形DEC的面积,需先求出一份的面积。
4.16-8×6÷4=4(平方分米) 提示:三角形BAE与三角形CAE等底等高,则它们的面积相等。从这两个三角形中同时减去三角形AEF,则剩下的面积相等,即三角形ABF与三角形CEF的面积相等。要求四边形EFGH的面积,就相当于用图中阴影部分的面积减去三角形DGC的面积。
5.15÷3=5(厘米) 12×5=60(平方厘米) 提示:过E点作CD的平行线,交BC于点F(如图),由此可看出,平行四边形ABFE的面积就是题中梯形与三角形的面积差,也就是15平方厘米。因为平行四边形ABFE的底AE长3厘米,所以它的高,也就是平行四边形ABCD的高就是15÷3=5(厘米)。因此,平行四边形ABCD的面积是12×5=60(平方厘米)。
6.20×30÷2=300(平方厘米) 300×2÷(20+30)=12(厘米) 12×30÷2=180(平方厘米) 提示:如图连接BE。观察发现,三角形ABC与三角形EBC等底等高,则它们的面积相等。由此可推出,S△ABC +S△BDC=S△EBC+S△BDC,即S△ADC=S△EBD。三角形ADC(三角形EDB)的面积为20×30÷2=300(平方厘米),BC的长为300×2÷(20+30)=12(厘米),三角形ABC的面积为12×30÷2=180(平方厘米)。
7.90÷2=45(平方厘米) 提示:从题图中可以看出角形ABF与三角形ABD的高相等,AD=3AF,则形ABD的面积是三角形ABF面积的3倍;同理可得,三角形ABD的面积是三角形BDE面积的3倍。由此可以推出,三角形ABF与三角形BDE的面积相等。若从这两个三角形中同时减去三角形BOE,则剩下的图形面积相等,即:四边形AEOF与三角形BOD的面积相等。因为三角形BOD的面积是平行四边BODC面积的一半,所以四边形AEOF的面积也是行四边形BODC面积的一半。故四边形AEOF的面积为90÷2=45(平方厘米)。
8.方法一:8-10×2÷4=3(厘米) 提示:如图,连接OA、OB。观察发现,三角形AEO与三角形GEO等底高,则它们的面积相等:同理,三角形BEO与三角CEO的面积相等。由此可推出,S△AEO+S△BEO=S△GEO+S△CEO,S△AOB=S阴影△GEC。根据三角形
AOB面积是10平方厘米,底AB的长是4厘米,可求出OE的长为10×2÷4=5(厘米)。然后用EF的长减OE的长,就可以求出OF的长为8-5=3(厘米)。
方法二:8×4÷2-10=6(平方厘米) 6×2÷4=3(厘米) 提示:如图,连接DE、DO观察发现,三角GEO与三角形DEO等底等高,则它们的面积相等。用三角形ECD的面积减去阴影部分的面积,就可求出三角形OCD的面积为8×4÷2-10=6(平方厘米)。三角形OCD的底CD的长为4厘米,则它的高OF的长为6×2÷4=3(厘米)。
9.4×4÷2=8(平方分米) (4÷2)×4÷2=4(平方分米)
8-8÷2-4÷2=2(平方分米) 提示:如图,连接BE。观察发现三角形EBC、三角形DBC都与形ABCD等底等高,它们的面积都是正方形ABCD面积的一半,面积为4×4÷2=8(平方分米)。由于E为AD的中点,则三角形DEC的面积为(4+2)×4÷2=4(平方分米)。由于P为CE的中点,则三角形DEP与三角DCP等底等高,面积相等,三角形DCP的面积相当于三角形DEC面积的一半,面积为4÷2=2(平方分米);同理,三角形BCP的面积为8÷2=4(平方分米)。
要求三角形BPD(阴影部分)的面积,只需用三角形DBC的面积分别减去三角形BCP的面积和三角形DCP的面积,列式为8-4-2=2(平方分米)。
