五年级上册数学试题-6.4《组合图形的面积》分层训练 人教新课标含答案
文档属性
| 名称 | 五年级上册数学试题-6.4《组合图形的面积》分层训练 人教新课标含答案 | 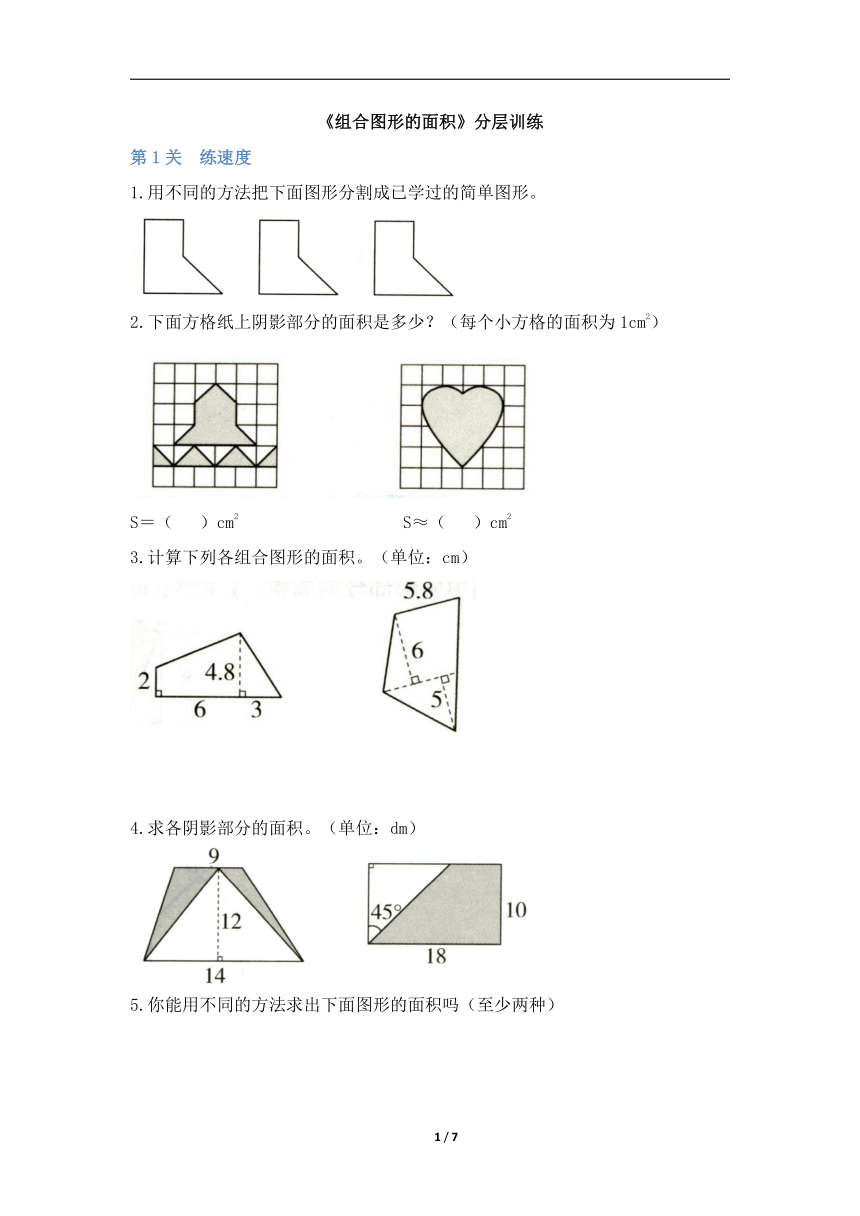 | |
| 格式 | zip | ||
| 文件大小 | 1.1MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-02-12 19:07:04 | ||
图片预览

文档简介
《组合图形的面积》分层训练
第1关 练速度
1.用不同的方法把下面图形分割成已学过的简单图形。
2.下面方格纸上阴影部分的面积是多少?(每个小方格的面积为1cm2)
S=( )cm2 S≈( )cm2
3.计算下列各组合图形的面积。(单位:cm)
4.求各阴影部分的面积。(单位:dm)
5.你能用不同的方法求出下面图形的面积吗(至少两种)
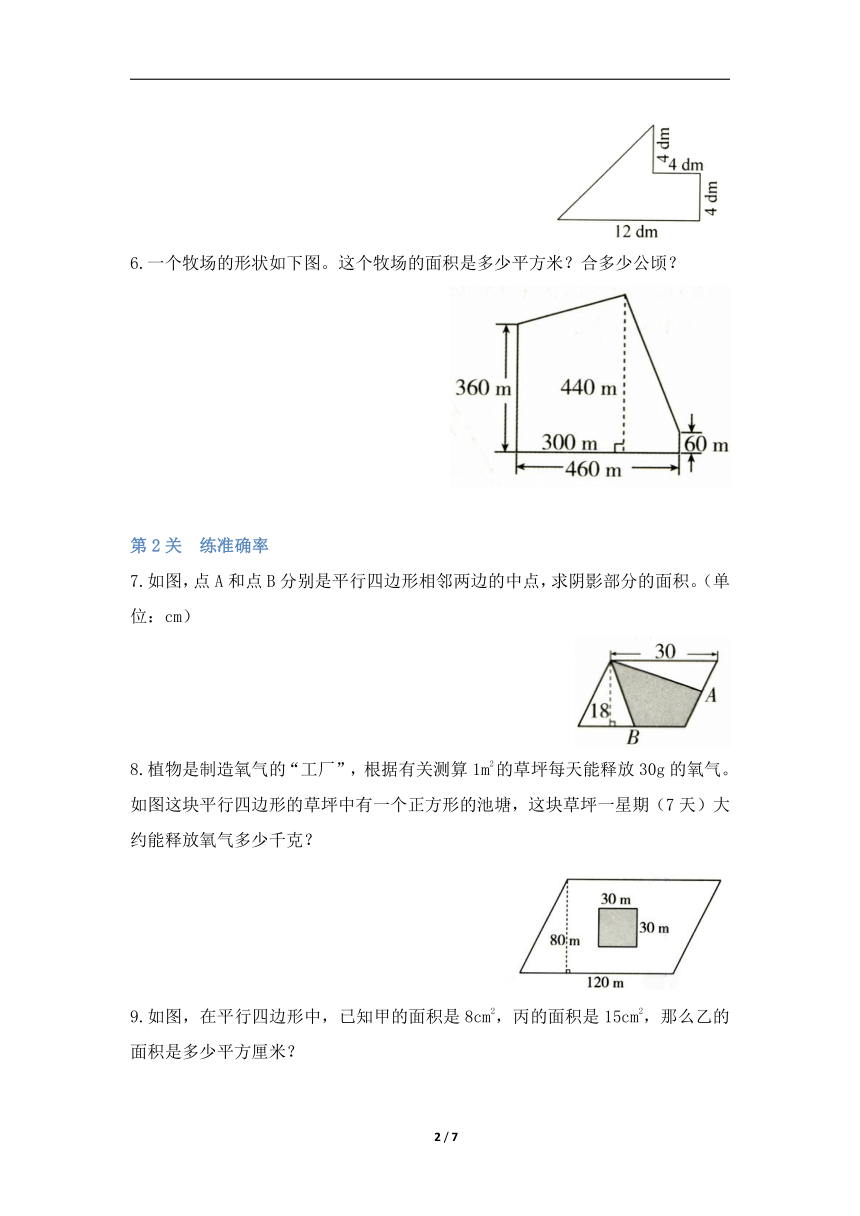
6.一个牧场的形状如下图。这个牧场的面积是多少平方米?合多少公顷?
第2关 练准确率
7.如图,点A和点B分别是平行四边形相邻两边的中点,求阴影部分的面积。(单位:cm)
8.植物是制造氧气的“工厂”,根据有关测算1m2的草坪每天能释放30g的氧气。如图这块平行四边形的草坪中有一个正方形的池塘,这块草坪一星期(7天)大约能释放氧气多少千克?
9.如图,在平行四边形中,已知甲的面积是8cm2,丙的面积是15cm2,那么乙的面积是多少平方厘米?
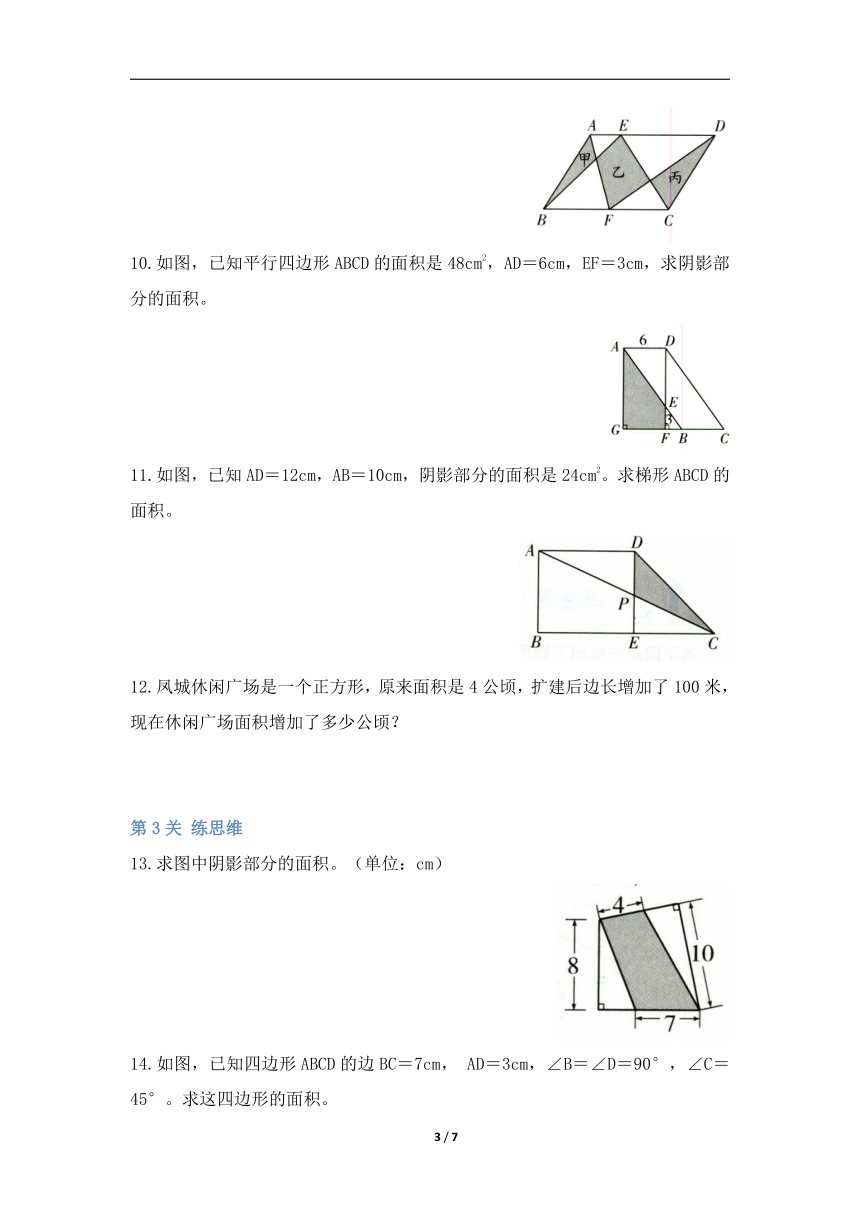
10.如图,已知平行四边形ABCD的面积是48cm2,AD=6cm,EF=3cm,求阴影部分的面积。
11.如图,已知AD=12cm,AB=10cm,阴影部分的面积是24cm2。求梯形ABCD的面积。
12.凤城休闲广场是一个正方形,原来面积是4公顷,扩建后边长增加了100米,现在休闲广场面积增加了多少公顷?
第3关 练思维
13.求图中阴影部分的面积。(单位:cm)
14.如图,已知四边形ABCD的边BC=7cm, AD=3cm,∠B=∠D=90°,∠C=45°。求这四边形的面积。
参考答案:
1.答案不唯一,如图:
2.9 9
3.(2+4.8)×6÷2+3×4.8÷2=27.6(cm2)
5.8×6+5.8×5÷2=49.3(cm2)
4.(9+14)×12÷2-14×12÷2=54(dm2)或9×12÷2=54(dm2)
18×10-10×10÷2=130(dm2)
5.方法如下:
S=(12-4)×(4+4)÷2+4×4=48(平方分米)
S=(4+12)×(4+4)÷2-4×4=48(平方分米)
6.(360+440)×300÷2+(440+60)×(460-300)÷2=160000(平方米)
160000平方米=16公顷
7.30×18÷2=270(cm2) 提示:如图,连接平行四边形的对角线,不难发现阴影部分面积等于空白部分面积,则阴影部分面积就是平行四边形面积的一半。
8.120×80-30×30=8700(m2) 30÷1000×8700×7=1827(kg)
9.连接EF,因为三角形ABF与三角形BFE同底等高,所以S三角形ABF=S三角形BFE,同理S三角形EFC=S三角形DFC,所以乙的面积=8+15=23(cm2)。
10.48÷6=8(cm) (3+8)×6÷2=3(cm2) 提示:从图中可以看出用平行四边形的面积除以底可得出平行四边形的高,这个高也就是梯形的下底,再根据梯形的面积公式求出阴影部分的面积。
11.12×10÷2-24=36(cm2) 36×2÷12=6(cm)
24×2÷6=8(cm) (12+12+8)×10÷2=160(cm2)
提示:从图中可以看出三角形ACD的底是12cm,高是10cm,则面积是12×10÷2=60(cm2),可得三角形ADP的面积为60-24=36(cm2),进而可求出PD的长,再根据三角形PCD的面积可求出三角形PCD的高即EC的长,这样就能求出梯形ABCD的面积。
12.4公顷=40000平方米 40000=200×200
200+100=300(米) 300×300=90000(平方米)
9000平方米=9公顷 9-4=5(公顷)
提示:先画出如图所示的示意图,从图上可以看出,增加的面积应该用扩建后的面积减去原来的面积,也就是用边长300米的正方形的面积减去4公顷。
13.7×8÷2+4×10÷2=48(cm2) 提示:连接阴影部分四边形的一条对角线,分割成一个底是4cm、高是10cm的三角形和另一个底是7cm、高是8cm的三角形。14.7×7÷2-3×3÷2=20(cm2) 提示:延长边BA和边CD,相交于点E(如图),使整个图形构成一个等腰直角三角形(三角形ADE也是等腰直角三角形)然后用等腰直角三角形EBC的面积减去等腰直角三角形ADE的面积,即得到四边形ABCD的面积。
第1关 练速度
1.用不同的方法把下面图形分割成已学过的简单图形。
2.下面方格纸上阴影部分的面积是多少?(每个小方格的面积为1cm2)
S=( )cm2 S≈( )cm2
3.计算下列各组合图形的面积。(单位:cm)
4.求各阴影部分的面积。(单位:dm)
5.你能用不同的方法求出下面图形的面积吗(至少两种)
6.一个牧场的形状如下图。这个牧场的面积是多少平方米?合多少公顷?
第2关 练准确率
7.如图,点A和点B分别是平行四边形相邻两边的中点,求阴影部分的面积。(单位:cm)
8.植物是制造氧气的“工厂”,根据有关测算1m2的草坪每天能释放30g的氧气。如图这块平行四边形的草坪中有一个正方形的池塘,这块草坪一星期(7天)大约能释放氧气多少千克?
9.如图,在平行四边形中,已知甲的面积是8cm2,丙的面积是15cm2,那么乙的面积是多少平方厘米?
10.如图,已知平行四边形ABCD的面积是48cm2,AD=6cm,EF=3cm,求阴影部分的面积。
11.如图,已知AD=12cm,AB=10cm,阴影部分的面积是24cm2。求梯形ABCD的面积。
12.凤城休闲广场是一个正方形,原来面积是4公顷,扩建后边长增加了100米,现在休闲广场面积增加了多少公顷?
第3关 练思维
13.求图中阴影部分的面积。(单位:cm)
14.如图,已知四边形ABCD的边BC=7cm, AD=3cm,∠B=∠D=90°,∠C=45°。求这四边形的面积。
参考答案:
1.答案不唯一,如图:
2.9 9
3.(2+4.8)×6÷2+3×4.8÷2=27.6(cm2)
5.8×6+5.8×5÷2=49.3(cm2)
4.(9+14)×12÷2-14×12÷2=54(dm2)或9×12÷2=54(dm2)
18×10-10×10÷2=130(dm2)
5.方法如下:
S=(12-4)×(4+4)÷2+4×4=48(平方分米)
S=(4+12)×(4+4)÷2-4×4=48(平方分米)
6.(360+440)×300÷2+(440+60)×(460-300)÷2=160000(平方米)
160000平方米=16公顷
7.30×18÷2=270(cm2) 提示:如图,连接平行四边形的对角线,不难发现阴影部分面积等于空白部分面积,则阴影部分面积就是平行四边形面积的一半。
8.120×80-30×30=8700(m2) 30÷1000×8700×7=1827(kg)
9.连接EF,因为三角形ABF与三角形BFE同底等高,所以S三角形ABF=S三角形BFE,同理S三角形EFC=S三角形DFC,所以乙的面积=8+15=23(cm2)。
10.48÷6=8(cm) (3+8)×6÷2=3(cm2) 提示:从图中可以看出用平行四边形的面积除以底可得出平行四边形的高,这个高也就是梯形的下底,再根据梯形的面积公式求出阴影部分的面积。
11.12×10÷2-24=36(cm2) 36×2÷12=6(cm)
24×2÷6=8(cm) (12+12+8)×10÷2=160(cm2)
提示:从图中可以看出三角形ACD的底是12cm,高是10cm,则面积是12×10÷2=60(cm2),可得三角形ADP的面积为60-24=36(cm2),进而可求出PD的长,再根据三角形PCD的面积可求出三角形PCD的高即EC的长,这样就能求出梯形ABCD的面积。
12.4公顷=40000平方米 40000=200×200
200+100=300(米) 300×300=90000(平方米)
9000平方米=9公顷 9-4=5(公顷)
提示:先画出如图所示的示意图,从图上可以看出,增加的面积应该用扩建后的面积减去原来的面积,也就是用边长300米的正方形的面积减去4公顷。
13.7×8÷2+4×10÷2=48(cm2) 提示:连接阴影部分四边形的一条对角线,分割成一个底是4cm、高是10cm的三角形和另一个底是7cm、高是8cm的三角形。14.7×7÷2-3×3÷2=20(cm2) 提示:延长边BA和边CD,相交于点E(如图),使整个图形构成一个等腰直角三角形(三角形ADE也是等腰直角三角形)然后用等腰直角三角形EBC的面积减去等腰直角三角形ADE的面积,即得到四边形ABCD的面积。
