2019秋北师大版九年级数学上册4.4探索三角形相似的条件学案(含3课时,无答案)
文档属性
| 名称 | 2019秋北师大版九年级数学上册4.4探索三角形相似的条件学案(含3课时,无答案) |  | |
| 格式 | zip | ||
| 文件大小 | 324.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-02-12 00:02:30 | ||
图片预览


文档简介
2019秋北师大版九年级数学上册第四章图形的相似4探索三角形相似的条件学案
第1课时 两角分别相等的两个三角形相似
学习
目标
1.经历两个三角形相似的探索过程;
2.能说出识别两个三角形相似的方法:有两个角分别相等的两个三角形相似;
3.会用这种方法判断两个三角形是否相似。
学习
重点难点
掌握相似三角形的判定定理,并能熟练地运用时重点也是难点
导 学 过 程
学法指导
一.交流预习:
1、判定两个三角形全等有哪些方法;
2、判定两个三角形相似是否一定要知道他们的对应角相等,对应边成比例呢?
3、相似三角形的判定方法有哪些?
二.合作探究
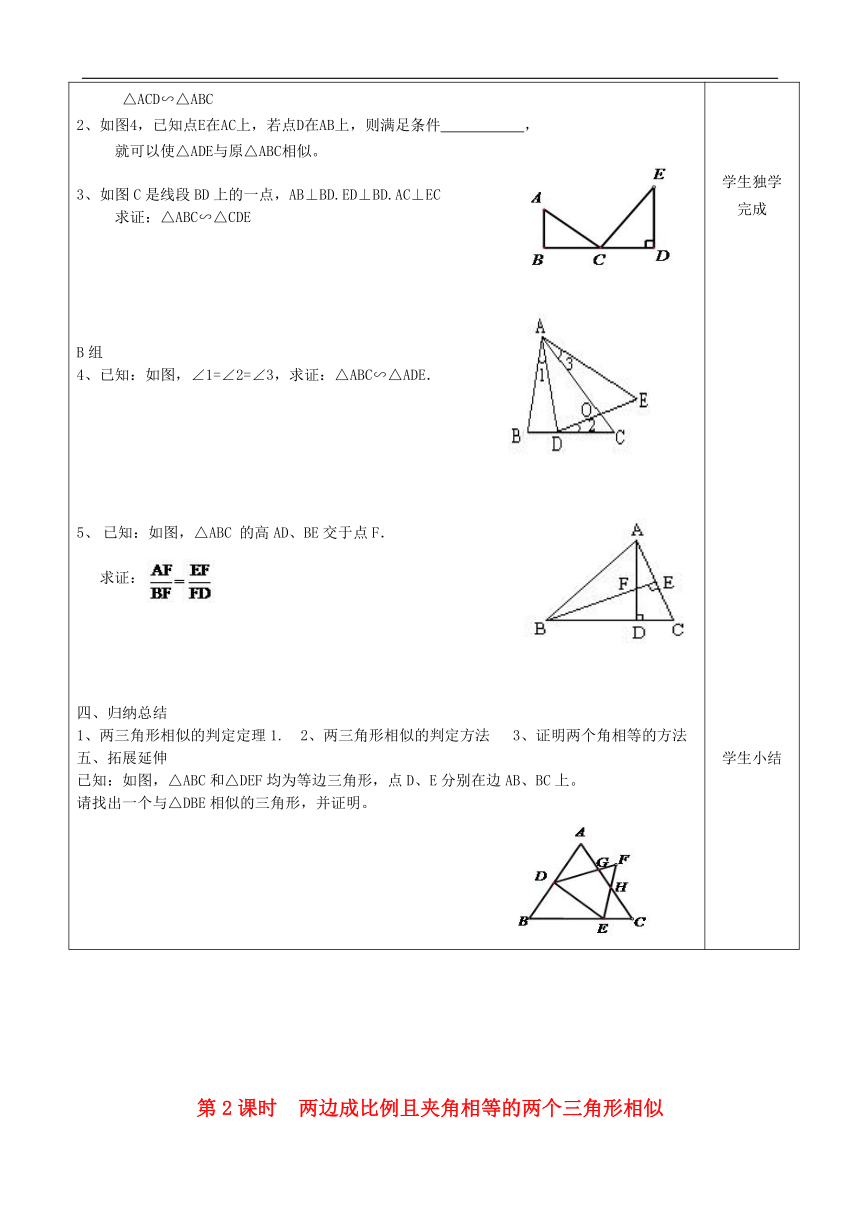
已知,如图,在△ABC和△A’B’C’中,
∠A=∠A’, ∠B=∠B’.
求证:△ABC∽△A’B’C’
相似三角形的判定定理1:___________________________________________
几何语言:
想一想:
有一个锐角对应相等的两个直角三角形是否相似?为什么?
等边三角形都相似吗?
各有一个内角为100°的两个等腰三角形是否相似?为什么?
△ABC和△A′B′C′中∠A=80°、∠B=40°、∠A′=80°、∠C′=60°.那么这两个三角形相似吗?
例题讲解:
已知:如图,在Rt△ABC中,CD是斜边AB上的高。请找出图中的相似三角形,并说明理由。
试一试:你能由例1的结论得到下面的关系式吗?为什么?
1、AC2=AD·AB 2、BC2=BD·AB 3、CD2=AD.BD 4、AC.BC=AB.CD
三、分层提高
A组
1、如图3,点D在AB上,当∠ =∠ 时,
△ACD∽△ABC
2、如图4,已知点E在AC上,若点D在AB上,则满足条件 ,
就可以使△ADE与原△ABC相似。
3、如图C是线段BD上的一点,AB⊥BD.ED⊥BD.AC⊥EC
求证:△ABC∽△CDE
B组
4、已知:如图,∠1=∠2=∠3,求证:△ABC∽△ADE.
已知:如图,△ABC 的高AD、BE交于点F.
求证:
四、归纳总结
1、两三角形相似的判定定理1. 2、两三角形相似的判定方法 3、证明两个角相等的方法
五、拓展延伸
已知:如图,△ABC和△DEF均为等边三角形,点D、E分别在边AB、BC上。
请找出一个与△DBE相似的三角形,并证明。
小组讨论
完成
由师生合作完成
学生独学
完成
学生小结
第2课时 两边成比例且夹角相等的两个三角形相似
学习
目标
掌握“两边成比例且夹角相等的两个三角形相似”的判定方法。
学习重点难点
重点:掌握判定方法,会运用判定方法判定两个三角形相似.
难点:会准确的运用三角形相似的条件来判定三角形是否相似.
导 学 过 程
学法指导
交流预习:
1、相似三角形的判定方法哪些?
2、全等三角形的判定方法有:______________________________________
3、我们已学过“两边及其夹角相等的两三角形全等”
.类似的,你能得到两三角形相似的新的判定方法吗?
二.合作探究
求证:两个三角形的两组对应边的比相等,且它们的夹角相等,那么这两个三角形相似.
例:已知:在△ABC和△DEF中,∠A=120°,AB=7cm,AC=14cm;
∠D=120°,DE =6cm, DF=3cm
求证:△ABC和△DEF相似
三、分层提高
1在△ABC中,∠B=30°,AB=5cm,AC=4cm;在△A|B|C|中,∠B|=30°,A|B|=10cm,A|C|=8cm.
判断两三角形是否相似。
2.已知: 如图,AB?AC=AD?AE,且∠1=∠2,
求证:△ABC∽△AED.
3.如图,在△ABC中,点D在AB上,请再添一个适当的条件,使△ADC∽△ACB,那么可添加的条件是 .
4.如图,在正方形ABCD中,E为AB的中点,BF=BC,试判断与△AED相似的三角形.并说明理由。
四、归纳总结:
能力提升:
5.如图,ΔABC与ΔADB中,∠ABC=∠ADB=90°,AC=5cm,AB=4cm,如果图中的两个直角三角形相似,求AD的长.
由师生合作完成
自己画图
写出已知
求证
并证明
学生独学
完成
(组长检查)
由师生合作完成
学生小结
第3课时 三边成比例的两个三角形相似
学习
目标
1、经历判定两个三角形相似条件的探索过程,积累数学活动的经验。
2、了解两个三角形相似的判定方法3,并能灵活运用解决实际问题。
3、能综合运用三种方法判定两个三角形相似。
学习重点难点
重点:理解并熟练掌握判定方法3成立的条件,并能用其来解决实际问题。
难点:探索相似三角形的判定方法.
导 学 过 程
学法指导
交流预习:
1、如图,在△ABC中,点D在AB上,请再添一个适当的条件,
使△ADC∽△ACB,那么可添加的条件是 .
2、相似三角形的判定方法已经学过那些?
二.合作探究
已知:在△ABC和△DEF中,
求证:△ABC∽△DEF
相似三角形的判定定理(三)______________________________________________
几何语言表达(如上图):
∵
∴
例题:已知:△ABC与△A’B’C’中,AB=4 cm,BC=6cm,AC=8cm,
A’B’=12cm, B’C’=18cm,A’C’=24cm.
求证:△ABC ∽△A’B’C’
三、分层提高
1.下列四个三角形,与左图中的三角形相似的是( )
2.一个直角三角形的两边长分别为3和6,另一个直角三角形的两边长
分别为2和4,那么这两个直角三角形 相似.(填“一定”、“不一定”、“一定不”).
3.下列图形中两个三角形是否相似?
4.已知:在ABC和△A′B′C′中AB=10cm,BC=8cm,AC=16cm,
A′B′=16cm,B′C′=12.8cm,A′C′=25.6cm;
求证△ABC和△A′B′C′相似。
5、已知:,求证:∠=∠.
B C
四、归纳总结
拓展:如图,某地四个乡镇A、B、C、D之间建有公路,
已知AB=14千米,AD=28千米, BD=21千米,
BC=42千米,DC=31.5千米,公路AB与CD平行吗?
说出你的理由。
由师生合作完成
由师生合作完成
学生叙述
师强调
独学完成
师生合作完成
学生小结
第1课时 两角分别相等的两个三角形相似
学习
目标
1.经历两个三角形相似的探索过程;
2.能说出识别两个三角形相似的方法:有两个角分别相等的两个三角形相似;
3.会用这种方法判断两个三角形是否相似。
学习
重点难点
掌握相似三角形的判定定理,并能熟练地运用时重点也是难点
导 学 过 程
学法指导
一.交流预习:
1、判定两个三角形全等有哪些方法;
2、判定两个三角形相似是否一定要知道他们的对应角相等,对应边成比例呢?
3、相似三角形的判定方法有哪些?
二.合作探究
已知,如图,在△ABC和△A’B’C’中,
∠A=∠A’, ∠B=∠B’.
求证:△ABC∽△A’B’C’
相似三角形的判定定理1:___________________________________________
几何语言:
想一想:
有一个锐角对应相等的两个直角三角形是否相似?为什么?
等边三角形都相似吗?
各有一个内角为100°的两个等腰三角形是否相似?为什么?
△ABC和△A′B′C′中∠A=80°、∠B=40°、∠A′=80°、∠C′=60°.那么这两个三角形相似吗?
例题讲解:
已知:如图,在Rt△ABC中,CD是斜边AB上的高。请找出图中的相似三角形,并说明理由。
试一试:你能由例1的结论得到下面的关系式吗?为什么?
1、AC2=AD·AB 2、BC2=BD·AB 3、CD2=AD.BD 4、AC.BC=AB.CD
三、分层提高
A组
1、如图3,点D在AB上,当∠ =∠ 时,
△ACD∽△ABC
2、如图4,已知点E在AC上,若点D在AB上,则满足条件 ,
就可以使△ADE与原△ABC相似。
3、如图C是线段BD上的一点,AB⊥BD.ED⊥BD.AC⊥EC
求证:△ABC∽△CDE
B组
4、已知:如图,∠1=∠2=∠3,求证:△ABC∽△ADE.
已知:如图,△ABC 的高AD、BE交于点F.
求证:
四、归纳总结
1、两三角形相似的判定定理1. 2、两三角形相似的判定方法 3、证明两个角相等的方法
五、拓展延伸
已知:如图,△ABC和△DEF均为等边三角形,点D、E分别在边AB、BC上。
请找出一个与△DBE相似的三角形,并证明。
小组讨论
完成
由师生合作完成
学生独学
完成
学生小结
第2课时 两边成比例且夹角相等的两个三角形相似
学习
目标
掌握“两边成比例且夹角相等的两个三角形相似”的判定方法。
学习重点难点
重点:掌握判定方法,会运用判定方法判定两个三角形相似.
难点:会准确的运用三角形相似的条件来判定三角形是否相似.
导 学 过 程
学法指导
交流预习:
1、相似三角形的判定方法哪些?
2、全等三角形的判定方法有:______________________________________
3、我们已学过“两边及其夹角相等的两三角形全等”
.类似的,你能得到两三角形相似的新的判定方法吗?
二.合作探究
求证:两个三角形的两组对应边的比相等,且它们的夹角相等,那么这两个三角形相似.
例:已知:在△ABC和△DEF中,∠A=120°,AB=7cm,AC=14cm;
∠D=120°,DE =6cm, DF=3cm
求证:△ABC和△DEF相似
三、分层提高
1在△ABC中,∠B=30°,AB=5cm,AC=4cm;在△A|B|C|中,∠B|=30°,A|B|=10cm,A|C|=8cm.
判断两三角形是否相似。
2.已知: 如图,AB?AC=AD?AE,且∠1=∠2,
求证:△ABC∽△AED.
3.如图,在△ABC中,点D在AB上,请再添一个适当的条件,使△ADC∽△ACB,那么可添加的条件是 .
4.如图,在正方形ABCD中,E为AB的中点,BF=BC,试判断与△AED相似的三角形.并说明理由。
四、归纳总结:
能力提升:
5.如图,ΔABC与ΔADB中,∠ABC=∠ADB=90°,AC=5cm,AB=4cm,如果图中的两个直角三角形相似,求AD的长.
由师生合作完成
自己画图
写出已知
求证
并证明
学生独学
完成
(组长检查)
由师生合作完成
学生小结
第3课时 三边成比例的两个三角形相似
学习
目标
1、经历判定两个三角形相似条件的探索过程,积累数学活动的经验。
2、了解两个三角形相似的判定方法3,并能灵活运用解决实际问题。
3、能综合运用三种方法判定两个三角形相似。
学习重点难点
重点:理解并熟练掌握判定方法3成立的条件,并能用其来解决实际问题。
难点:探索相似三角形的判定方法.
导 学 过 程
学法指导
交流预习:
1、如图,在△ABC中,点D在AB上,请再添一个适当的条件,
使△ADC∽△ACB,那么可添加的条件是 .
2、相似三角形的判定方法已经学过那些?
二.合作探究
已知:在△ABC和△DEF中,
求证:△ABC∽△DEF
相似三角形的判定定理(三)______________________________________________
几何语言表达(如上图):
∵
∴
例题:已知:△ABC与△A’B’C’中,AB=4 cm,BC=6cm,AC=8cm,
A’B’=12cm, B’C’=18cm,A’C’=24cm.
求证:△ABC ∽△A’B’C’
三、分层提高
1.下列四个三角形,与左图中的三角形相似的是( )
2.一个直角三角形的两边长分别为3和6,另一个直角三角形的两边长
分别为2和4,那么这两个直角三角形 相似.(填“一定”、“不一定”、“一定不”).
3.下列图形中两个三角形是否相似?
4.已知:在ABC和△A′B′C′中AB=10cm,BC=8cm,AC=16cm,
A′B′=16cm,B′C′=12.8cm,A′C′=25.6cm;
求证△ABC和△A′B′C′相似。
5、已知:,求证:∠=∠.
B C
四、归纳总结
拓展:如图,某地四个乡镇A、B、C、D之间建有公路,
已知AB=14千米,AD=28千米, BD=21千米,
BC=42千米,DC=31.5千米,公路AB与CD平行吗?
说出你的理由。
由师生合作完成
由师生合作完成
学生叙述
师强调
独学完成
师生合作完成
学生小结
同课章节目录
- 第一章 特殊平行四边形
- 1 菱形的性质与判定
- 2 矩形的性质与判定
- 3 正方形的性质与判定
- 第二章 一元二次方程
- 1 认识一元二次方程
- 2 用配方法求解一元二次方程
- 3 用公式法求解一元二次方程
- 4 用因式分解法求解一元二次方程
- 5 一元二次方程的根与系数的关系
- 6 应用一元二次方程
- 第三章 概率的进一步认识
- 1 用树状图或表格求概率
- 2 用频率估计概率
- 第四章 图形的相似
- 1 成比例线段
- 2 平行线分线段成比例
- 3 相似多边形
- 4 探索三角形相似的条件
- 5 相似三角形判定定理的证明
- 6 利用相似三角形测高
- 7 相似三角形的性质
- 8 图形的位似
- 第五章 投影与视图
- 1 投影
- 2 视图
- 第六章 反比例函数
- 1 反比例函数
- 2 反比例函数的图象与性质
- 3 反比例函数的应用
