苏科版七年级数学下册7.2平行线的判定与性质复习课课件(共43张PPT)
文档属性
| 名称 | 苏科版七年级数学下册7.2平行线的判定与性质复习课课件(共43张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 296.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-02-12 00:00:00 | ||
图片预览






文档简介
课件43张PPT。 平行线的判定与性质
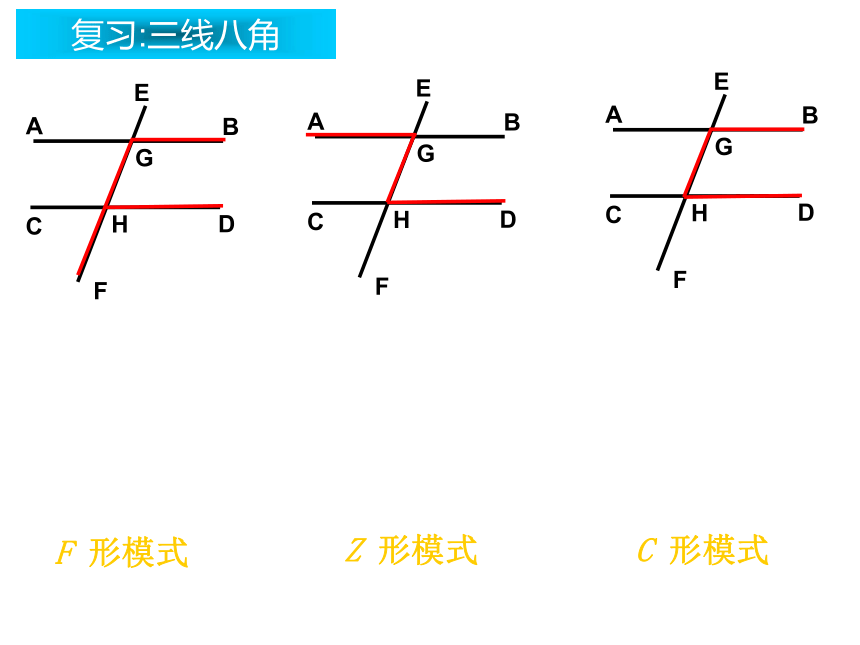
复习课复习:三线八角F 形模式Z 形模式C 形模式1、判定两条直线平行有哪些方法?在这些方法中,已经知道
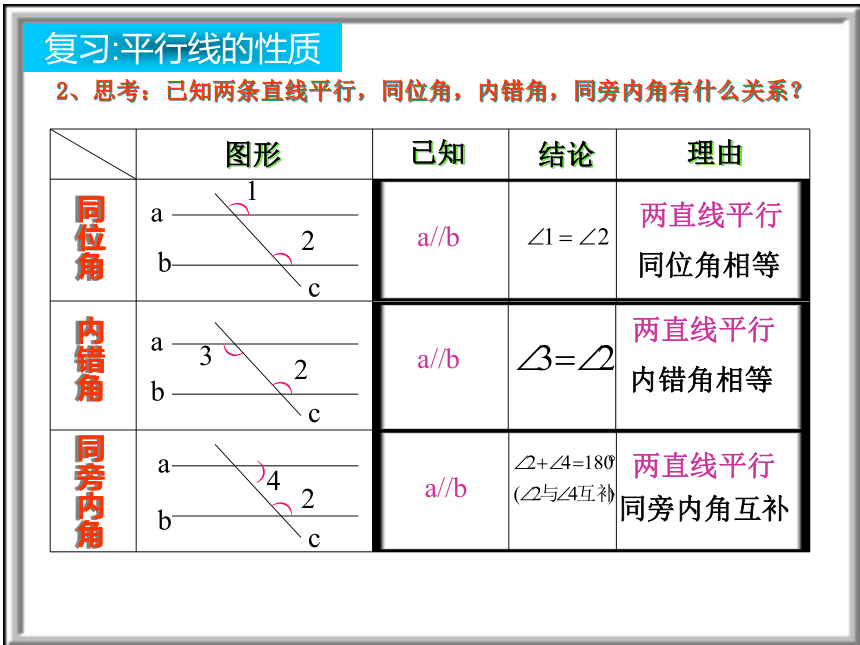
了什么?得到的结果是什么?图形已知结论理由同位角内错角同旁内角a//ba//ba//b同位角相等
两直线平行内错角相等
两直线平行同旁内角互补
两直线平行122324))))))abababccc复习:平行线的判定图形已知结论理由同位角内错角同旁内角a//ba//b内错角相等
两直线平行同旁内角互补
两直线平行122324))))))abababccca//b同位角相等
两直线平行a//b两直线平行同位角相等a//b两直线平行内错角相等同旁内角互补a//b两直线平行2、思考:已知两条直线平行,同位角,内错角,同旁内角有什么关系?复习:平行线的性质感悟模式2、思考:已知两条直线平行有哪些性质?在这些性质中,已经知道了什么关系?得到的结果是什么关系?即同位角,内错角,同旁内角有什么关系?1、未知两条直线平行有哪些方法?在这些方法中,已经知道了什么关系?得到的结果是什么关系?如图1,直线a、b、c被直线l所截,若∠1=∠2=∠3.
由∠1=∠2可以知道 ∥ ,它的根据是 。
由∠1=∠3可以知道 ∥ ,它的根据是 。 abca同位角相等,两直线平行内错角相等,两直线平行感悟模式 如图,若∠1=∠2,则 ∥ ;
理由是 ;
若∠3=∠4,则 ∥ ;
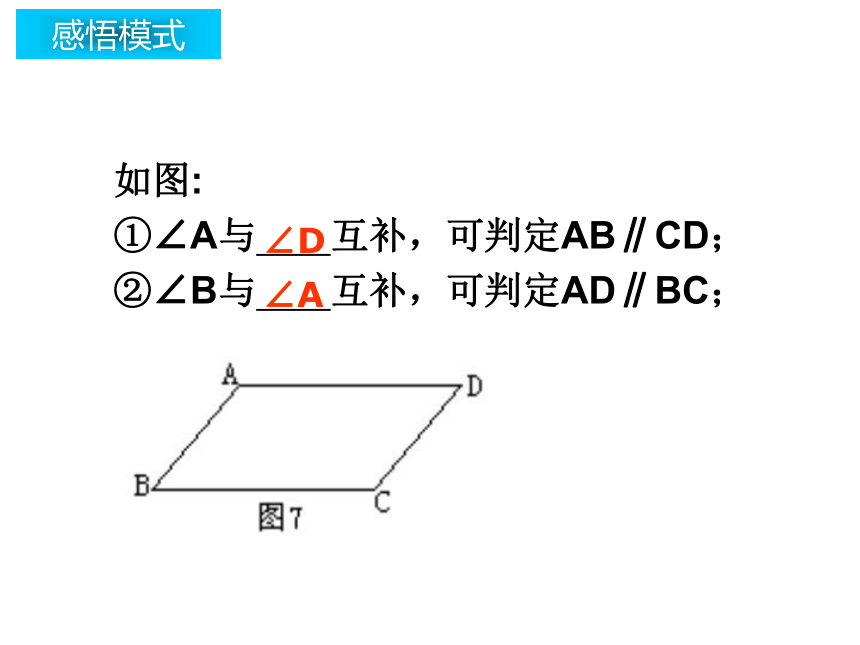
理由是 ;ADBC内错角相等,两直线平行ABDC内错角相等,两直线平行感悟模式如图:
①∠A与 互补,可判定AB∥CD;
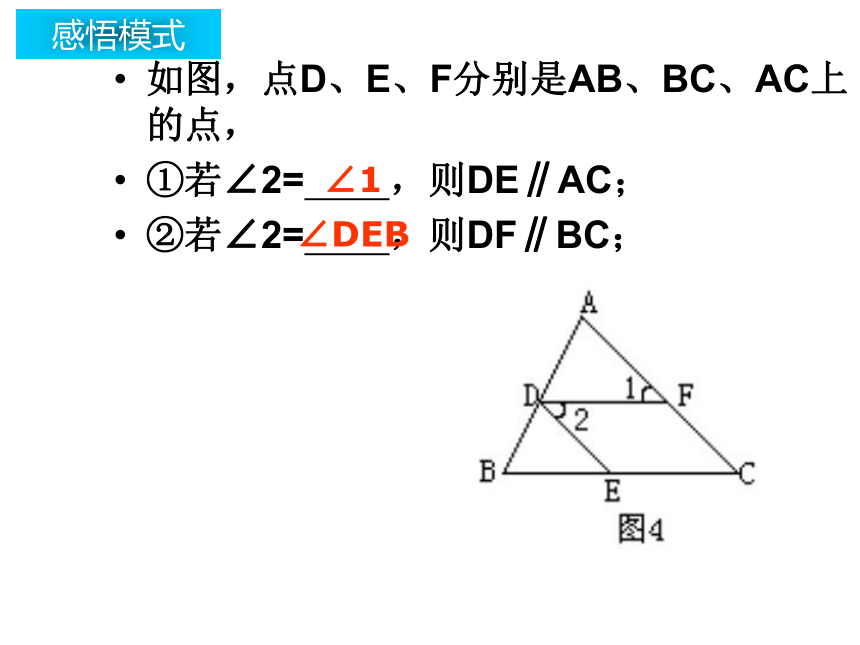
②∠B与 互补,可判定AD∥BC;∠D∠A感悟模式如图,点D、E、F分别是AB、BC、AC上的点,
①若∠2= ,则DE∥AC;
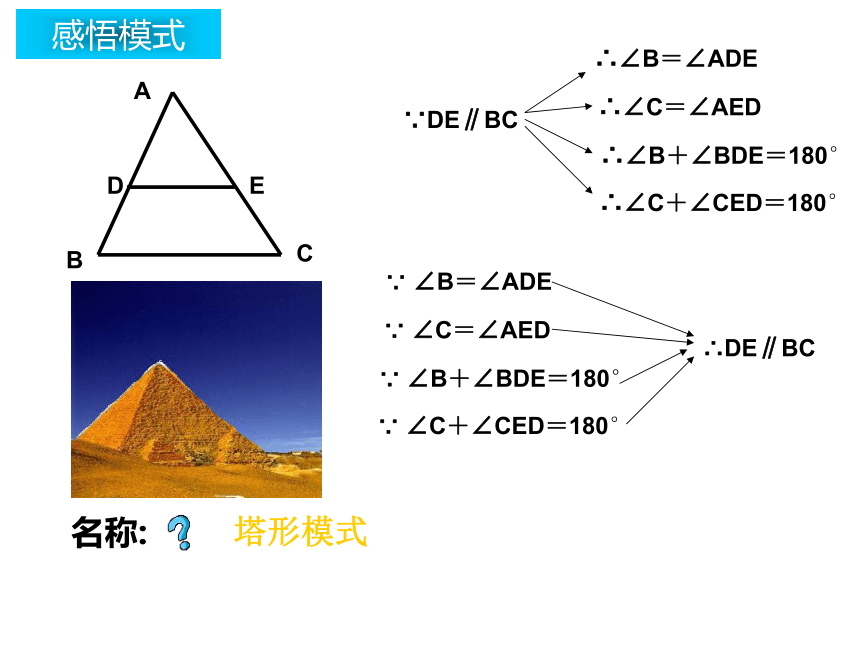
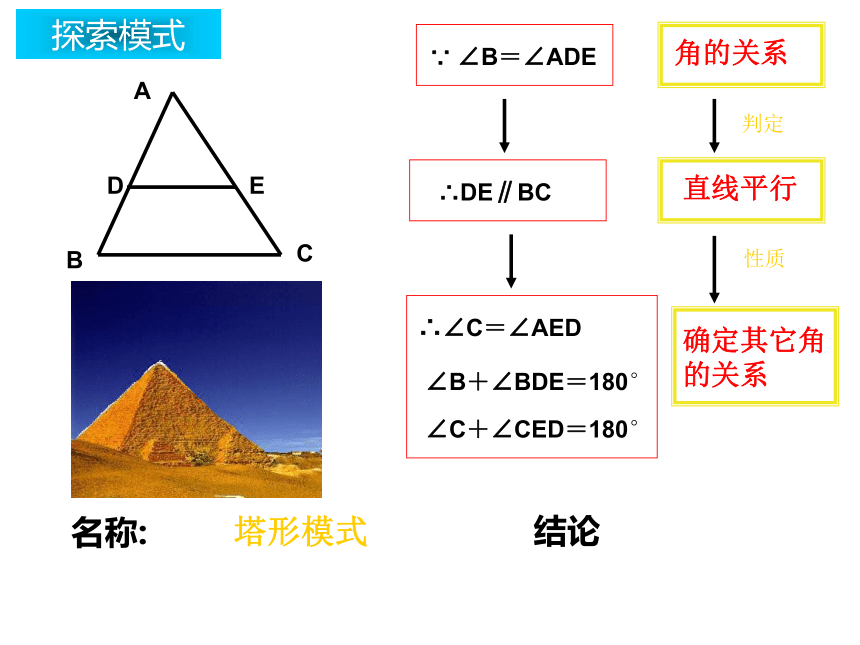
②若∠2= ,则DF∥BC;∠1∠DEB感悟模式感悟模式∵DE∥BC∴DE∥BC塔形模式探索模式ABCDE名称:塔形模式结论感悟模式ABCDO∵AB∥CD∵ ∠B=∠D∵ ∠C=∠A∴DE∥BC蝶形模式探索模式ABCDO名称:蝶形模式结论应用模式ABCDEF123塔形模式Z 形模式塔形模式应用模式 如图,若AB∥DF,∠2=∠A,试确定DE与AC的位置关系,并说明理由.ABCDEF2应用模式如图,图中包含哪些基本模式?ABCDEFO应用模式 已知,如图AB∥EF∥CD,AC∥BD,BC平分∠ABC,则图中
与∠EOD相等的角有( )个.A. 2B. 3C. 4D. 5D应用模式①下图中包含哪些基本模式?②已知:∠1=∠2,∠C=∠D,
求证:DF∥AC③已知:∠A=∠F,∠C=∠D,
求证:DF∥ACABCDEF12分析和处理
(1)由已知条件∠1=∠2,你可以得到什么?
(2)结合图形,你可以得到什么?
(3)要说明AB∥CD,只需要满足什么条件?问题1、如图,当∠1=∠2时, AB与CD平行吗?为什么?问题2
已知:∠1=∠2
试说明∠3与∠4的关系问题3、已知:如图,?1=?2=?B,EF∥AB。
问:?3和?C有什么数量关系?为什么?
问题4、 已知:CD∥EF, ∠1= ∠2,求证: ∠AGD= ∠ACB。证明:∵CD ∥EF ( )(2)已知: CD∥EF, ∠AGD= ∠ACB.
求证: ∠1= ∠2(3)已知:∠AGD= ∠ACB
∠1= ∠2.
求证: CD∥EF.∴ ∠ AGD= ∠ ACB ( )∴DG ∥BC ( )∴ ∠1= ∠3 ( )∵ ∠1= ∠2 ( )∴ ∠2= ∠3 ( )问题5、如图,AB∥CD,∠1=∠2,∠E=37°,求:∠F。问:如右图所示,若AB∥CD,则
∠AEC与∠A、∠C 的关系如何?问题探究 已知:AB∥CD,
求证:∠A+ ∠ C+ ∠ AEC=360°证明:过E点作EF ∥ AB,则∠A+ ∠ 1= 180° ,
∵AB∥CD( )
∴ EF ∥CD(平行于同一直线的两直线互相平行)
∴ ∠2+ ∠ C= 180° ( )
∴ ∠A+ ∠ 1 +∠2+ ∠ C= 360° ( )
即∠A+ ∠ C+ ∠ AEC= 360° ( )
探究2、如图甲:已知AB∥DE,那么∠1+∠2+∠3等于多少度?试加以说明。 当已知条件不变,而图形变为如图乙时,结论改变了吗?图丙中的∠1+∠2+∠3+∠4是多少度呢?如果如丁图所示,∠1+∠2+∠3+…+∠n的和又为多少度?你找到了什么规律吗? 若∠1与∠2的关系为内错角,∠1=40°,
则∠2等于( )
A.40° B. 140°
C. 40°或140° D. 不确定D练一练:如图 , a // b,且∠2是∠1的2倍,
那么∠2等于( )
A. 60° B. 90° C. 120° D. 150° 练一练:C如图,已知:∠2=∠3,∠1+∠3=180°, 说明EF∥GH. 练一练:如图,已知AD//BC,∠1=∠2,∠A=100°,且BD⊥CD,
则∠ABC=_____,∠C=_____.练一练:80°50°如图,OP∥QR∥ST,则下列各式中正确的是????( )
A.∠1+∠2+∠3=180°
B.∠1+∠2-∠3=90°
C.∠1-∠2+∠3=90°
D.∠2+∠3-∠1=180°练一练:D如图,CD平分∠ACB,DE∥AC,且∠1=35°,求∠2的度数.12练一练: 已知:AB∥CD,MG、NH分别平分∠EMB和∠DNM,那么MG与NH的关系怎样?
练一练: 已知:AB∥CD,MG、NH分别平分∠NMB和∠CNM,那么,MG与NH的关系怎样?
练一练:
已知:AB//DE,∠1=∠2
说明AC//DF
练一练:已知:如图,?1=?2=?B,EF∥AB。
问:?3和?C有什么数量关系?为什么?练一练: 如图,已知BF平分∠ABC,∠CEB=∠CBE=65°,∠EDF=50°
说明:BC∥AF练一练:如图,AB∥CD,∠1=∠2,∠E=37°,求:∠F练一练:
已知:CD∥EF, ∠1= ∠2,
说明 ∠AGD= ∠ACB。(2)已知: CD∥EF, ∠AGD= ∠ACB.
说明 ∠1= ∠2(3)已知:∠AGD= ∠ACB
∠1= ∠2.
说明 CD∥EF.练一练:问:如右图所示,若AB∥CD,则
∠AEC与∠A、∠C 的关系如何?问题探究
已知:AB∥CD,
求∠A+ ∠ C+ ∠ AEC如图, AB∥CD,点B是∠AOC的平分线OE的反向延长线与AB的交点,且∠A+ ∠C =70°,
∠B=25°,求∠C的度数.想一想:课堂小结:
1、通过习题你有何收获?
要判定两条直线平行,可以运用哪些公理或定理?
要判定两个角相等或互补,可以运用哪些公理或定理?
2、思想方法:
分析问题的方法:
由已知看可知,扩大已知面。
由未知想需知,明确解题方向
识图的方法:
在定理图形中提炼基本图形,
在解题时把复杂图形分解为基本图形 重要做到“五会”(1)会表达:能正确地叙述概念的定义。
(2)会识图:能在较复杂的图形中识别出概念所反映的部分。
(3)会翻译:能结合图形把概念的定义翻译成符号语言。
(4)会画图:能画出概念所反映的几何图形,以及变式图形,会在图上标注字母或符号。
(5)会应用:能应用概念进行简单的判断、推理和计算。结束寄语严格性之于数学家,犹如道德之于人.
由“因”导“果”,言必有据.是初学证明者谨记和遵循的原则.
了什么?得到的结果是什么?图形已知结论理由同位角内错角同旁内角a//ba//ba//b同位角相等
两直线平行内错角相等
两直线平行同旁内角互补
两直线平行122324))))))abababccc复习:平行线的判定图形已知结论理由同位角内错角同旁内角a//ba//b内错角相等
两直线平行同旁内角互补
两直线平行122324))))))abababccca//b同位角相等
两直线平行a//b两直线平行同位角相等a//b两直线平行内错角相等同旁内角互补a//b两直线平行2、思考:已知两条直线平行,同位角,内错角,同旁内角有什么关系?复习:平行线的性质感悟模式2、思考:已知两条直线平行有哪些性质?在这些性质中,已经知道了什么关系?得到的结果是什么关系?即同位角,内错角,同旁内角有什么关系?1、未知两条直线平行有哪些方法?在这些方法中,已经知道了什么关系?得到的结果是什么关系?如图1,直线a、b、c被直线l所截,若∠1=∠2=∠3.
由∠1=∠2可以知道 ∥ ,它的根据是 。
由∠1=∠3可以知道 ∥ ,它的根据是 。 abca同位角相等,两直线平行内错角相等,两直线平行感悟模式 如图,若∠1=∠2,则 ∥ ;
理由是 ;
若∠3=∠4,则 ∥ ;
理由是 ;ADBC内错角相等,两直线平行ABDC内错角相等,两直线平行感悟模式如图:
①∠A与 互补,可判定AB∥CD;
②∠B与 互补,可判定AD∥BC;∠D∠A感悟模式如图,点D、E、F分别是AB、BC、AC上的点,
①若∠2= ,则DE∥AC;
②若∠2= ,则DF∥BC;∠1∠DEB感悟模式感悟模式∵DE∥BC∴DE∥BC塔形模式探索模式ABCDE名称:塔形模式结论感悟模式ABCDO∵AB∥CD∵ ∠B=∠D∵ ∠C=∠A∴DE∥BC蝶形模式探索模式ABCDO名称:蝶形模式结论应用模式ABCDEF123塔形模式Z 形模式塔形模式应用模式 如图,若AB∥DF,∠2=∠A,试确定DE与AC的位置关系,并说明理由.ABCDEF2应用模式如图,图中包含哪些基本模式?ABCDEFO应用模式 已知,如图AB∥EF∥CD,AC∥BD,BC平分∠ABC,则图中
与∠EOD相等的角有( )个.A. 2B. 3C. 4D. 5D应用模式①下图中包含哪些基本模式?②已知:∠1=∠2,∠C=∠D,
求证:DF∥AC③已知:∠A=∠F,∠C=∠D,
求证:DF∥ACABCDEF12分析和处理
(1)由已知条件∠1=∠2,你可以得到什么?
(2)结合图形,你可以得到什么?
(3)要说明AB∥CD,只需要满足什么条件?问题1、如图,当∠1=∠2时, AB与CD平行吗?为什么?问题2
已知:∠1=∠2
试说明∠3与∠4的关系问题3、已知:如图,?1=?2=?B,EF∥AB。
问:?3和?C有什么数量关系?为什么?
问题4、 已知:CD∥EF, ∠1= ∠2,求证: ∠AGD= ∠ACB。证明:∵CD ∥EF ( )(2)已知: CD∥EF, ∠AGD= ∠ACB.
求证: ∠1= ∠2(3)已知:∠AGD= ∠ACB
∠1= ∠2.
求证: CD∥EF.∴ ∠ AGD= ∠ ACB ( )∴DG ∥BC ( )∴ ∠1= ∠3 ( )∵ ∠1= ∠2 ( )∴ ∠2= ∠3 ( )问题5、如图,AB∥CD,∠1=∠2,∠E=37°,求:∠F。问:如右图所示,若AB∥CD,则
∠AEC与∠A、∠C 的关系如何?问题探究 已知:AB∥CD,
求证:∠A+ ∠ C+ ∠ AEC=360°证明:过E点作EF ∥ AB,则∠A+ ∠ 1= 180° ,
∵AB∥CD( )
∴ EF ∥CD(平行于同一直线的两直线互相平行)
∴ ∠2+ ∠ C= 180° ( )
∴ ∠A+ ∠ 1 +∠2+ ∠ C= 360° ( )
即∠A+ ∠ C+ ∠ AEC= 360° ( )
探究2、如图甲:已知AB∥DE,那么∠1+∠2+∠3等于多少度?试加以说明。 当已知条件不变,而图形变为如图乙时,结论改变了吗?图丙中的∠1+∠2+∠3+∠4是多少度呢?如果如丁图所示,∠1+∠2+∠3+…+∠n的和又为多少度?你找到了什么规律吗? 若∠1与∠2的关系为内错角,∠1=40°,
则∠2等于( )
A.40° B. 140°
C. 40°或140° D. 不确定D练一练:如图 , a // b,且∠2是∠1的2倍,
那么∠2等于( )
A. 60° B. 90° C. 120° D. 150° 练一练:C如图,已知:∠2=∠3,∠1+∠3=180°, 说明EF∥GH. 练一练:如图,已知AD//BC,∠1=∠2,∠A=100°,且BD⊥CD,
则∠ABC=_____,∠C=_____.练一练:80°50°如图,OP∥QR∥ST,则下列各式中正确的是????( )
A.∠1+∠2+∠3=180°
B.∠1+∠2-∠3=90°
C.∠1-∠2+∠3=90°
D.∠2+∠3-∠1=180°练一练:D如图,CD平分∠ACB,DE∥AC,且∠1=35°,求∠2的度数.12练一练: 已知:AB∥CD,MG、NH分别平分∠EMB和∠DNM,那么MG与NH的关系怎样?
练一练: 已知:AB∥CD,MG、NH分别平分∠NMB和∠CNM,那么,MG与NH的关系怎样?
练一练:
已知:AB//DE,∠1=∠2
说明AC//DF
练一练:已知:如图,?1=?2=?B,EF∥AB。
问:?3和?C有什么数量关系?为什么?练一练: 如图,已知BF平分∠ABC,∠CEB=∠CBE=65°,∠EDF=50°
说明:BC∥AF练一练:如图,AB∥CD,∠1=∠2,∠E=37°,求:∠F练一练:
已知:CD∥EF, ∠1= ∠2,
说明 ∠AGD= ∠ACB。(2)已知: CD∥EF, ∠AGD= ∠ACB.
说明 ∠1= ∠2(3)已知:∠AGD= ∠ACB
∠1= ∠2.
说明 CD∥EF.练一练:问:如右图所示,若AB∥CD,则
∠AEC与∠A、∠C 的关系如何?问题探究
已知:AB∥CD,
求∠A+ ∠ C+ ∠ AEC如图, AB∥CD,点B是∠AOC的平分线OE的反向延长线与AB的交点,且∠A+ ∠C =70°,
∠B=25°,求∠C的度数.想一想:课堂小结:
1、通过习题你有何收获?
要判定两条直线平行,可以运用哪些公理或定理?
要判定两个角相等或互补,可以运用哪些公理或定理?
2、思想方法:
分析问题的方法:
由已知看可知,扩大已知面。
由未知想需知,明确解题方向
识图的方法:
在定理图形中提炼基本图形,
在解题时把复杂图形分解为基本图形 重要做到“五会”(1)会表达:能正确地叙述概念的定义。
(2)会识图:能在较复杂的图形中识别出概念所反映的部分。
(3)会翻译:能结合图形把概念的定义翻译成符号语言。
(4)会画图:能画出概念所反映的几何图形,以及变式图形,会在图上标注字母或符号。
(5)会应用:能应用概念进行简单的判断、推理和计算。结束寄语严格性之于数学家,犹如道德之于人.
由“因”导“果”,言必有据.是初学证明者谨记和遵循的原则.
同课章节目录
- 第7章 平面图形的认识(二)
- 7.1 探索直线平行的条件
- 7.2 探索平行线的性质
- 7.3 图形的平移
- 7.4 认识三角形
- 7.5 多边形的内角和与外角和
- 第8章 幂的运算
- 8.1 同底数幂的乘法
- 8.2 幂的乘方与积的乘方
- 8.3 同底数幂的除法
- 第9章 整式乘法与因式分解
- 9.1 单项式乘单项式
- 9.2 单项式乘多项式
- 9.3 多项式乘多项式
- 9.4 乘法公式
- 9.5 多项式的因式分解
- 第10章 二元一次方程组
- 10.1 二元一次方程
- 10.2 二元一次方程组
- 10.3 解二元一次方程组
- 10.4 三元一次方程组
- 10.5 用二元一次方程解决问题
- 第11章 一元一次不等式
- 11.1 生活中的不等式
- 11.2 不等式的解集
- 11.3 不等式的性质
- 11.4 解一元一次不等式
- 11.5 用一元一次不等式解决问题
- 11.6 一元一次不等式组
- 第12章 证明
- 12.1 定义与命题
- 12.2 证明
- 12.3 互逆命题
