苏科版八年级数学下册第11章反比例函数复习课件(共57张PPT)
文档属性
| 名称 | 苏科版八年级数学下册第11章反比例函数复习课件(共57张PPT) |  | |
| 格式 | zip | ||
| 文件大小 | 741.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-02-12 08:34:02 | ||
图片预览





文档简介
课件57张PPT。 反比例函数 复习精品课件 1.进一步理解反比例函数的定义,会确定反
比例函数的解析式。
2.灵活掌握反比例函数的图象及性质。
3.运用反比例函数解决某些实际问题。学习目标 1 、下面函数中,哪些是反比例函数?
(1)(2) (3)(4)(5)基础知识回顾2.若双曲线经过点(-3 ,2),则其解析式是______.y=kx-1xy=k(k≠0)(k≠0)等价形式:(k≠0)反比例函数的定义4.函数 的图象在二、四象限内,m的取值
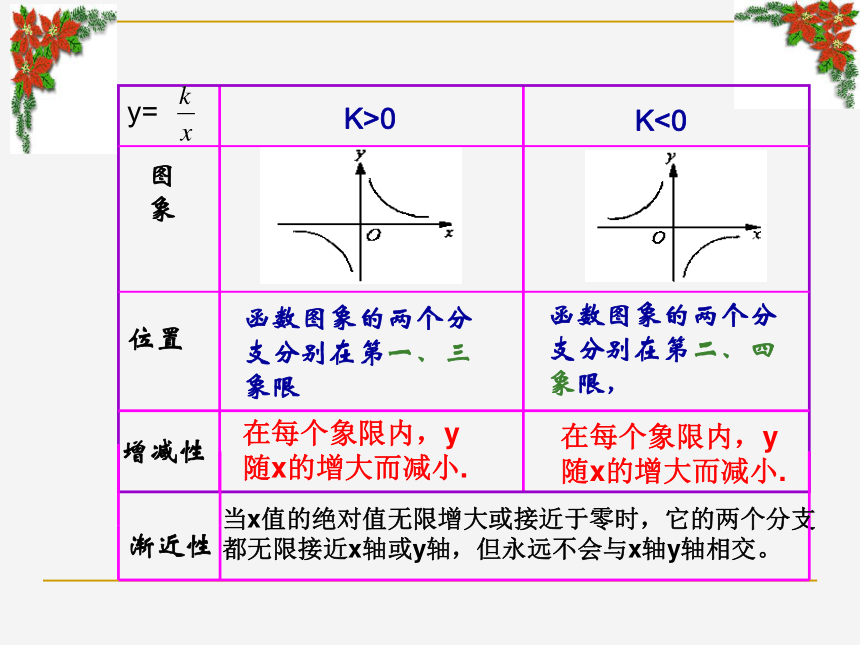
范围是______ .在每个象限内,y随x的增大而____m<23.函数 的图象在第______象限,当x<0时,
y随x的增大而______ .一、三减小增大K>0K<0函数图象的两个分支分别在第一、三象限函数图象的两个分支分别在第二、四象限,图
象位置y=渐近性在每个象限内,y随x的增大而减小.
在每个象限内,y随x的增大而减小.当x值的绝对值无限增大或接近于零时,它的两个分支
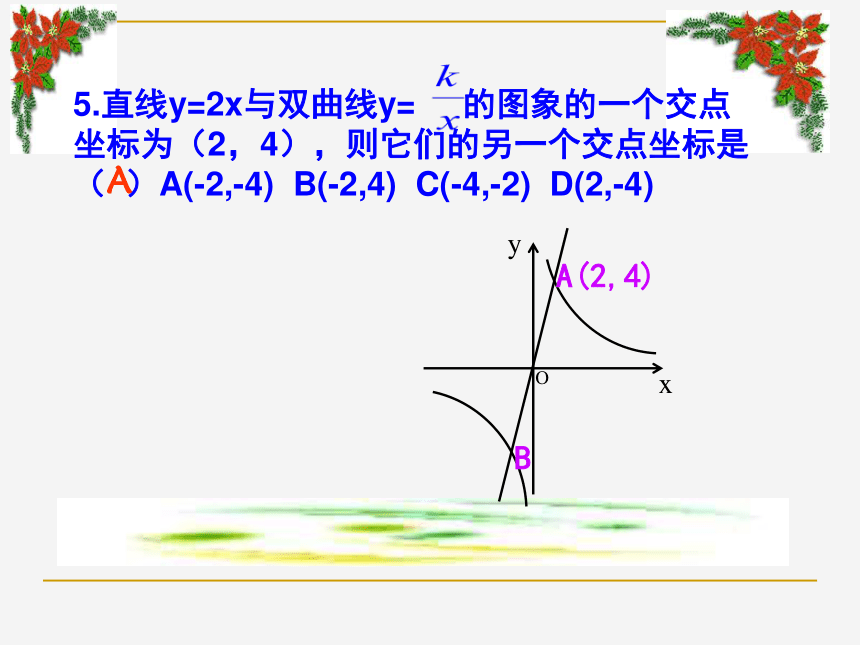
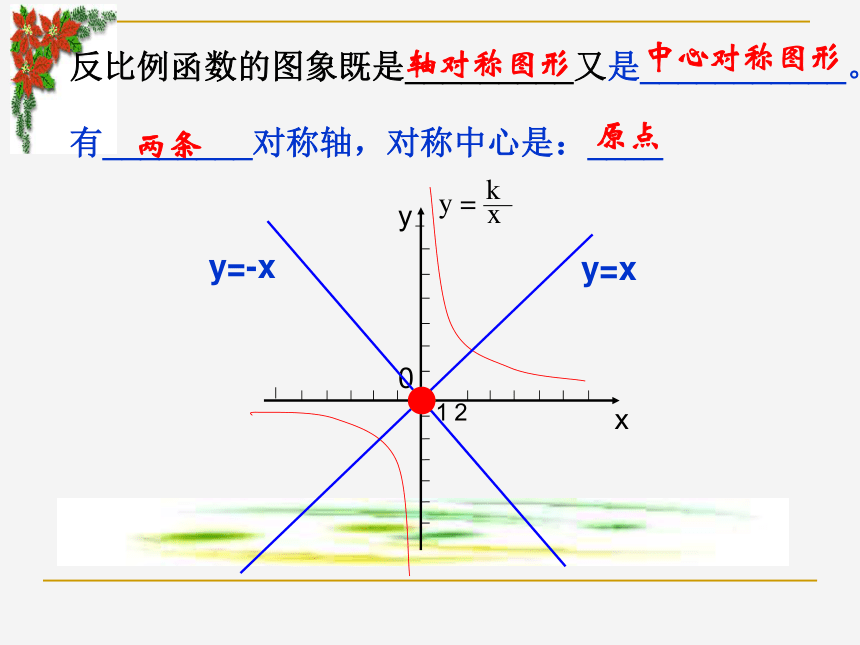
都无限接近x轴或y轴,但永远不会与x轴y轴相交。增减性5.直线y=2x与双曲线y= 的图象的一个交点坐标为(2,4),则它们的另一个交点坐标是( )A(-2,-4) B(-2,4) C(-4,-2) D(2,-4)A反比例函数的图象既是_________又是___________。
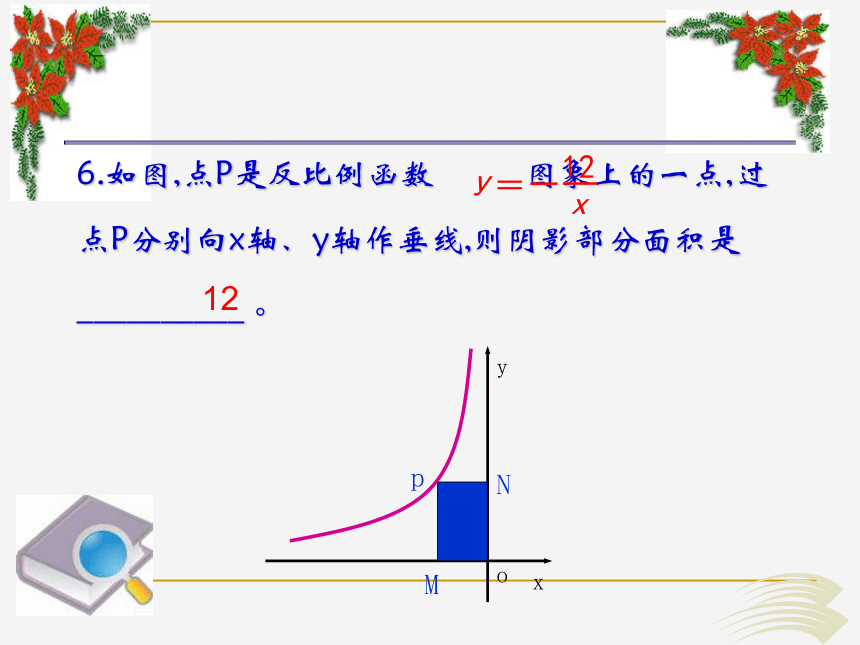
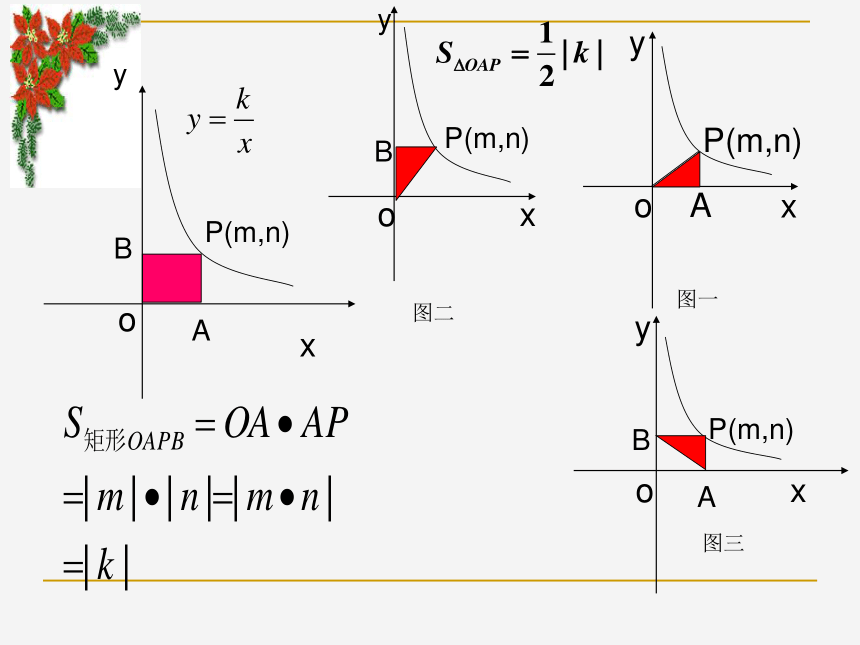
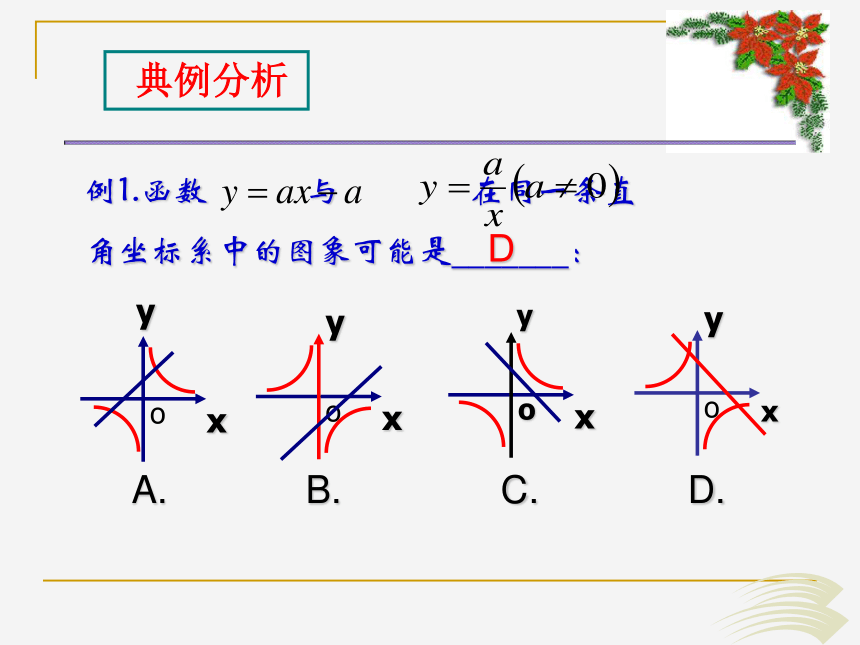
有________对称轴,对称中心是:____xy012轴对称图形中心对称图形原点●两条6.如图,点P是反比例函数 图象上的一点,过点P分别向x轴、y轴作垂线,则阴影部分面积是__________ 。12例1.函数 与 在同一条直
角坐标系中的图象可能是_______:D 典例分析D跟踪练习例2.已知点A(-2,y1),B(-1,y2)都在反比例函数 的图象上,则y1与y2的大小关系(从大到小)为 .y1> y2 典例分析y2> y1跟踪练习A(x1,y1),B(x2,y2)且x1<0<x2y1 >y2例3.如图,在平面直角坐标系中,A为y轴正半轴上一点,
过A作x轴的平行线,交函数
的图象于B,交函数 的图象于C,过C作y
轴的平行线交x轴于D.
四边形BODC的面积
为 . 7 典例分析2跟踪练习1、点A和点B在反比例函数上且线段AB经过点O,过点A、B分别作直线AC、BC平行于Y轴和X轴,两直线交于点C,则S⊿ABC的面积=____ 如图、一次函数 y1= ax+b 的图象和反比例
函数 的图象交于A(3,1)、B(n,-3)两点.
(1)求反比例函数和一次函数的解析式。
(2)x取何值时,y1﹥y2 。AB(2)当x﹥3 或 -1﹤x﹤0时, y1﹥y2 。 1C综合运用 为了预防“流感”,某学校对教室采用药熏消毒法进行
毒, 已知药物燃烧时,室内每立方米空气中的含药量y(mg)
与时间x(min)成正比例.药物燃烧后,y与x成反比例(如图所
示),现测得药物8min燃毕,此时室内空气中每立方米的含药
量为6mg,请根据题中所提供的信息,解答下列问题:
(1)药物燃烧时,y关于x 的函数关系式为: ________, 自变量x 的取值
范围是:__________,药物燃烧后y关于x的函数关系式为_____________.学以致用 为了预防“流感”,某学校对教室采用药熏消毒法进行毒, 已知药物燃烧时,室内每立方米空气中的含药量y(mg)与时间x(min)成正比例.药物燃烧后,y与x成反比例(如图所示),现测得药物8min燃毕,此时室内空气中每立方米的含药量为6mg,请根据题中所提供的信息,解答下列问题:
(2)研究表明,当空气中每立方米的含药量不低
于3mg且持续时间不低于10min时,才能有效杀
灭空气中的病菌,那么此次消毒是否有效?为什么?1.先求出教室中含氧量为3mg时的时间点2.再从图像中发现,当消毒过程处于这两个时间点之间时,教室中的含药量是大于等于3mg。3.将两个时间点相减后与10比较,发现本次消毒是有效的。做题时要注意数形结合小结1.反比例函数解析式常见的几种形式:2.反比例函数图像的形状,位置,增减性,对称性,
面积不变性。3.一些基本题型的解题要点4.反比例函数在生活中的应用5.做题时要注意数形结合1、必做题:一张试卷 2、选做题:心理学家研究发现,一般情况下,一节课40分钟中,学生的注意力随教师讲课的变化而变化.开始上课时,学生的注意力逐步增强,中间有一段时间学生的注意力保持较为理想的稳定状态,随后学生的注意力开始分散.经过实验分析可知,学生的注意力指标数y随时间x(分钟)的变化规律如右图所示(注:AB段为一次函数CD反比例函数
(1)开始上课后第五分钟时与第三十分钟时相比较,何时学生的注意力
更集中?
(2)一道数学竞赛题,需要讲19分钟,
为了效果较好,要求学生的注意力指标
数最低达到36,那么经过适当安排,老
师能否在学生注意力达到所需的状态下
讲解完这道题目? (五)分层作业K的几何意义:=OA·AP=|m| ·|n|=|k| 如图,点P是反比例函数图象上的一点,过点P分别向x轴、y轴作垂线,若阴影部分面积为12,则这个反比例函数的关系式是__________ 。变式一: 如图所示,正比例函数 与反比例函数 的图象相交于A、C两点,过A作x轴的垂线交x轴于B,连接BC.若△ABC面积为S,则______变式二:(A)s=1 (B) s=2
(C)1当x<-1或0A.1 B.2
C.S>2 D.1 (1)药物燃烧时,y关于x 的函数关系式为: ______, 自变量x 的取值范围是:_______,药物燃烧后y关于x的函数关系式为_______.
(2)研究表明,当空气中每立方米的含药量低于1.6mg时学生方可进教室,那么从消毒开始,至少需要经过多少分钟后,学生才能回到教室;
(3)研究表明,当空气中每立方米的含药量
不低于3mg且持续时间不低于10min时,才能
有效杀灭空气中的病菌,那么此次消毒是否
有效?为什么?
复习巩固:(应用)3.如图,点P是反比例函数 图象上的一点,PD⊥x轴于D.则△POD的面积为 .(m,n)1变1:如图,A、B是函数y= 的图象上关于原点对称 的任意两点,AC∥y轴,BC∥x轴,则△ABC的面积S为( )
A)1 B)2
C)S>2 D)1∴k=±12(X>0)ABC
下列图形中阴影部分的面积相等的是( )
A.①② B.②③ C.①③ C144mnA. S1>S2
B.S1C.S1=S2
D.S1与S2的大小关系
不能确定cS1S21、ACOxy解:当X=0时, y=2. 即 C (0 ,2)
当y=0时, x=2. 即 A (2 ,0)
∴S⊿AOC =2∴S四边形DCOE =4-2=2∴K=-2
面积性质(一)面积性质(二)面积性质(三)想一想
若将此题改为过P点作y轴的垂线段,其结论成立吗?以上几点揭示了双曲线上的点构成的几何图形的一类性质.掌握好这些性质,对解题十分有益.(上面图仅以P点在第一象限为例). ( 二)提升技能——图象性质设计意图:全面考查学生对反比例函数图象及性质的掌握。 ( 二)提升技能——图象性质设计意图:让学生进一步体会反比例函数的增减性,深刻领会“在每一象限内”的含义。 3、已知反比例函数 ,若(x1,y1),
(x2,y2),(x3,y3)在反比例函数图像上,
且 x1<0<x2<x3,其对应值 y1,y2 ,y3 的
大小关系是 。 (二)提升技能——学科整合设计意图:通过学科整合体现数学的应用价值,培养学生应用数学解决实际问题的能力。 4、已知力F所作用的功是15焦,则力F与物体在力的方向通过的距离S的图象大致是( ). (二)提升技能——学情反馈 1、若函数 是反比例函数,则m的值等于 .2、如图,P是反比例函数 图象上一点,若图中阴影部
分的矩形面积是2,则这个反比例函数的
解析式为 .
3、函数 与 ( ≠0)在同一
直角坐标系中的图象可能是( ). (三)深化应用——链接中考设计意图:反比例函数与一次函数的综合应用是近几年中考的热点,通过合作探究,有效地拓展思维,提升能力,进一步体会数形结合的思想。 如图,正比例函数 y x 的图象与反比例函
数 (k≠0)在第一象限的图象交于A点,过点A作x轴的
垂线,垂足为M,已知△OAM 的面积为1.
(1)求反比例函数的解析式;
(2)如果B为反比例函数在第一象限
图象上的点(点B与点A不重合),
且B点的横坐标为1 ,在x轴上
求一点P,使PA+PB最小.第九章 反比例函数
一、知识建构 二、典型例题
1、定义
2、图象 k﹥0
反比例函数 及其
性质 k﹤0
3、应用 (六)板书设计 1、 改变传统的复习模式,让学生自己动脑、动手梳理知识,培养学生自主学习的能力,变“要我学”为“我会学”。
2、采用展示交流的方式,培养学生的团队意识,激发学生的自信心和创新精神。
3、通过小组合作,让学生发现问题、分析问题、解决问题,体现以学生为主体,学生主动参与,积极探究,合作交流等新的教学模式。设计思路 题型三B4解题要点:形如下图中图形的面积S△ABC=︱K︱SABCD=2︱K︱BDx思考:
试归纳反比例函数的概念、图象与性质,并与正比例函数作比较.二、四增大<四理一理在每一个象限内:
当k>0时,y随x的增大而减小;
当k<0时,y随x的增大而增大.y=kx(k≠0)( 特殊的一次函数)当k>0时,y随x的增大而增大;
当k<0时,y随x的增大而减小.ABC
比例函数的解析式。
2.灵活掌握反比例函数的图象及性质。
3.运用反比例函数解决某些实际问题。学习目标 1 、下面函数中,哪些是反比例函数?
(1)(2) (3)(4)(5)基础知识回顾2.若双曲线经过点(-3 ,2),则其解析式是______.y=kx-1xy=k(k≠0)(k≠0)等价形式:(k≠0)反比例函数的定义4.函数 的图象在二、四象限内,m的取值
范围是______ .在每个象限内,y随x的增大而____m<23.函数 的图象在第______象限,当x<0时,
y随x的增大而______ .一、三减小增大K>0K<0函数图象的两个分支分别在第一、三象限函数图象的两个分支分别在第二、四象限,图
象位置y=渐近性在每个象限内,y随x的增大而减小.
在每个象限内,y随x的增大而减小.当x值的绝对值无限增大或接近于零时,它的两个分支
都无限接近x轴或y轴,但永远不会与x轴y轴相交。增减性5.直线y=2x与双曲线y= 的图象的一个交点坐标为(2,4),则它们的另一个交点坐标是( )A(-2,-4) B(-2,4) C(-4,-2) D(2,-4)A反比例函数的图象既是_________又是___________。
有________对称轴,对称中心是:____xy012轴对称图形中心对称图形原点●两条6.如图,点P是反比例函数 图象上的一点,过点P分别向x轴、y轴作垂线,则阴影部分面积是__________ 。12例1.函数 与 在同一条直
角坐标系中的图象可能是_______:D 典例分析D跟踪练习例2.已知点A(-2,y1),B(-1,y2)都在反比例函数 的图象上,则y1与y2的大小关系(从大到小)为 .y1> y2 典例分析y2> y1跟踪练习A(x1,y1),B(x2,y2)且x1<0<x2y1 >y2例3.如图,在平面直角坐标系中,A为y轴正半轴上一点,
过A作x轴的平行线,交函数
的图象于B,交函数 的图象于C,过C作y
轴的平行线交x轴于D.
四边形BODC的面积
为 . 7 典例分析2跟踪练习1、点A和点B在反比例函数上且线段AB经过点O,过点A、B分别作直线AC、BC平行于Y轴和X轴,两直线交于点C,则S⊿ABC的面积=____ 如图、一次函数 y1= ax+b 的图象和反比例
函数 的图象交于A(3,1)、B(n,-3)两点.
(1)求反比例函数和一次函数的解析式。
(2)x取何值时,y1﹥y2 。AB(2)当x﹥3 或 -1﹤x﹤0时, y1﹥y2 。 1C综合运用 为了预防“流感”,某学校对教室采用药熏消毒法进行
毒, 已知药物燃烧时,室内每立方米空气中的含药量y(mg)
与时间x(min)成正比例.药物燃烧后,y与x成反比例(如图所
示),现测得药物8min燃毕,此时室内空气中每立方米的含药
量为6mg,请根据题中所提供的信息,解答下列问题:
(1)药物燃烧时,y关于x 的函数关系式为: ________, 自变量x 的取值
范围是:__________,药物燃烧后y关于x的函数关系式为_____________.学以致用 为了预防“流感”,某学校对教室采用药熏消毒法进行毒, 已知药物燃烧时,室内每立方米空气中的含药量y(mg)与时间x(min)成正比例.药物燃烧后,y与x成反比例(如图所示),现测得药物8min燃毕,此时室内空气中每立方米的含药量为6mg,请根据题中所提供的信息,解答下列问题:
(2)研究表明,当空气中每立方米的含药量不低
于3mg且持续时间不低于10min时,才能有效杀
灭空气中的病菌,那么此次消毒是否有效?为什么?1.先求出教室中含氧量为3mg时的时间点2.再从图像中发现,当消毒过程处于这两个时间点之间时,教室中的含药量是大于等于3mg。3.将两个时间点相减后与10比较,发现本次消毒是有效的。做题时要注意数形结合小结1.反比例函数解析式常见的几种形式:2.反比例函数图像的形状,位置,增减性,对称性,
面积不变性。3.一些基本题型的解题要点4.反比例函数在生活中的应用5.做题时要注意数形结合1、必做题:一张试卷 2、选做题:心理学家研究发现,一般情况下,一节课40分钟中,学生的注意力随教师讲课的变化而变化.开始上课时,学生的注意力逐步增强,中间有一段时间学生的注意力保持较为理想的稳定状态,随后学生的注意力开始分散.经过实验分析可知,学生的注意力指标数y随时间x(分钟)的变化规律如右图所示(注:AB段为一次函数CD反比例函数
(1)开始上课后第五分钟时与第三十分钟时相比较,何时学生的注意力
更集中?
(2)一道数学竞赛题,需要讲19分钟,
为了效果较好,要求学生的注意力指标
数最低达到36,那么经过适当安排,老
师能否在学生注意力达到所需的状态下
讲解完这道题目? (五)分层作业K的几何意义:=OA·AP=|m| ·|n|=|k| 如图,点P是反比例函数图象上的一点,过点P分别向x轴、y轴作垂线,若阴影部分面积为12,则这个反比例函数的关系式是__________ 。变式一: 如图所示,正比例函数 与反比例函数 的图象相交于A、C两点,过A作x轴的垂线交x轴于B,连接BC.若△ABC面积为S,则______变式二:(A)s=1 (B) s=2
(C)1
C.S>2 D.1
(2)研究表明,当空气中每立方米的含药量低于1.6mg时学生方可进教室,那么从消毒开始,至少需要经过多少分钟后,学生才能回到教室;
(3)研究表明,当空气中每立方米的含药量
不低于3mg且持续时间不低于10min时,才能
有效杀灭空气中的病菌,那么此次消毒是否
有效?为什么?
复习巩固:(应用)3.如图,点P是反比例函数 图象上的一点,PD⊥x轴于D.则△POD的面积为 .(m,n)1变1:如图,A、B是函数y= 的图象上关于原点对称 的任意两点,AC∥y轴,BC∥x轴,则△ABC的面积S为( )
A)1 B)2
C)S>2 D)1
下列图形中阴影部分的面积相等的是( )
A.①② B.②③ C.①③ C144mnA. S1>S2
B.S1
D.S1与S2的大小关系
不能确定cS1S21、ACOxy解:当X=0时, y=2. 即 C (0 ,2)
当y=0时, x=2. 即 A (2 ,0)
∴S⊿AOC =2∴S四边形DCOE =4-2=2∴K=-2
面积性质(一)面积性质(二)面积性质(三)想一想
若将此题改为过P点作y轴的垂线段,其结论成立吗?以上几点揭示了双曲线上的点构成的几何图形的一类性质.掌握好这些性质,对解题十分有益.(上面图仅以P点在第一象限为例). ( 二)提升技能——图象性质设计意图:全面考查学生对反比例函数图象及性质的掌握。 ( 二)提升技能——图象性质设计意图:让学生进一步体会反比例函数的增减性,深刻领会“在每一象限内”的含义。 3、已知反比例函数 ,若(x1,y1),
(x2,y2),(x3,y3)在反比例函数图像上,
且 x1<0<x2<x3,其对应值 y1,y2 ,y3 的
大小关系是 。 (二)提升技能——学科整合设计意图:通过学科整合体现数学的应用价值,培养学生应用数学解决实际问题的能力。 4、已知力F所作用的功是15焦,则力F与物体在力的方向通过的距离S的图象大致是( ). (二)提升技能——学情反馈 1、若函数 是反比例函数,则m的值等于 .2、如图,P是反比例函数 图象上一点,若图中阴影部
分的矩形面积是2,则这个反比例函数的
解析式为 .
3、函数 与 ( ≠0)在同一
直角坐标系中的图象可能是( ). (三)深化应用——链接中考设计意图:反比例函数与一次函数的综合应用是近几年中考的热点,通过合作探究,有效地拓展思维,提升能力,进一步体会数形结合的思想。 如图,正比例函数 y x 的图象与反比例函
数 (k≠0)在第一象限的图象交于A点,过点A作x轴的
垂线,垂足为M,已知△OAM 的面积为1.
(1)求反比例函数的解析式;
(2)如果B为反比例函数在第一象限
图象上的点(点B与点A不重合),
且B点的横坐标为1 ,在x轴上
求一点P,使PA+PB最小.第九章 反比例函数
一、知识建构 二、典型例题
1、定义
2、图象 k﹥0
反比例函数 及其
性质 k﹤0
3、应用 (六)板书设计 1、 改变传统的复习模式,让学生自己动脑、动手梳理知识,培养学生自主学习的能力,变“要我学”为“我会学”。
2、采用展示交流的方式,培养学生的团队意识,激发学生的自信心和创新精神。
3、通过小组合作,让学生发现问题、分析问题、解决问题,体现以学生为主体,学生主动参与,积极探究,合作交流等新的教学模式。设计思路 题型三B4解题要点:形如下图中图形的面积S△ABC=︱K︱SABCD=2︱K︱BDx思考:
试归纳反比例函数的概念、图象与性质,并与正比例函数作比较.二、四增大<四理一理在每一个象限内:
当k>0时,y随x的增大而减小;
当k<0时,y随x的增大而增大.y=kx(k≠0)( 特殊的一次函数)当k>0时,y随x的增大而增大;
当k<0时,y随x的增大而减小.ABC
同课章节目录
- 第7章 数据的收集、整理、描述
- 7.1 普查与抽样调查
- 7.2 统计图的选用
- 7.3 频数和频率
- 7.4 频数分布表和频数分布直方图
- 第8章 认识概率
- 8.1 确定事件与随机事件
- 8.2 可能性的大小
- 8.3 频率与概率
- 第9章 中心对称图形——平行四边形
- 9.1 图形的旋转
- 9.2 中心对称与中心对称图形
- 9.3 平行四边形
- 9.4 矩形、菱形、正方形
- 9.5 三角形的中位线
- 第10章 分式
- 10.1 分式
- 10.2 分式的基本性质
- 10.3 分式的加减
- 10.4 分式的乘除
- 10.5 分式方程
- 第11章 反比例函数
- 11.1 反比例函数
- 11.2 反比例函数的图象与性质
- 11.3 用反比例函数解决问题
- 第12章 二次根式
- 12.1 二次根式
- 12.2 二次根式的乘除
- 12.3 二次根式的加减
