人教版八年级数学下册17.2勾股定理的逆定理同步练习解析版
文档属性
| 名称 | 人教版八年级数学下册17.2勾股定理的逆定理同步练习解析版 |  | |
| 格式 | zip | ||
| 文件大小 | 197.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-02-12 11:34:35 | ||
图片预览


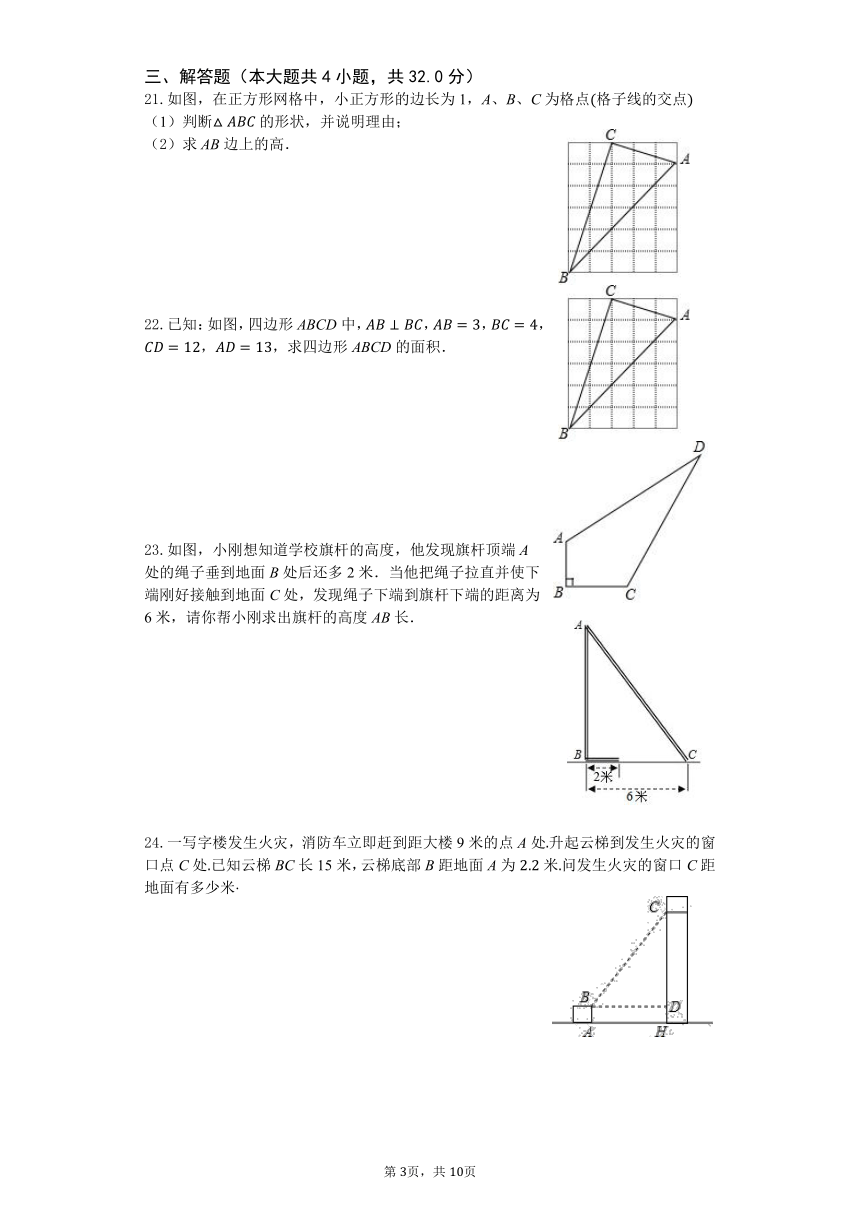


文档简介
17.2勾股定理的逆定理
一、选择题(本大题共10小题,共30.0分)
1.下列各组数是三角形的三边,能组成直角三角形的一组数是( )
A. 2,3,4 B. 3,4,5 C. 6,8,12 D.
2.下列各组数据中能作为直角三角形的三边长的是( )
A. 1,2,2 B. 1,1, C. 4,5,6 D. 1,,2
3.下列各组数中能作为直角三角形三边长的是( )
,12,15;,12,6;,12,14;,16,20
A. B. C. D.
4.在中,若AB:BC::4:5,则一定是( )
A. 锐角三角形 B. 钝角三角形 C. 直角三角形 D. 任意三角形
5.已知a、b、c是三角形的三边长,如果满足,则三角形的形状是( )
A. 底与边不相等的等腰三角形 B. 等边三角形
C. 钝角三角形 D. 直角三角形
6.如图,在高为3米,斜坡长为5米的楼梯台阶上铺地毯,则地毯的长度至少要( )
A. 4米 B. 5米 C. 6米 D. 7米
7.如图,学校有一块长方形花圃,有极少数人为了避开拐角走“捷径”,在花圃内走出了一条“路”他们仅仅少走了( )步路假设2步为1米,却踩伤了花草.
A. 1 B. 2 C. 3 D. 4
8.如图,在水池的正中央有一根芦苇,它高出水而1尺,水池宽10尺,如果把这根芦苇拉向水池一边,它的顶端恰好到达池边的水面,则这根芦苇的长度是( )
A. 10尺 B. 11尺 C. 12尺 D. 13尺
9.如图:长方形纸片ABCD中,,,按如图的方式折叠,使点B与点D重合.折痕为EF,则DE长为( )
A. ?cm B. 5?cm C. ?cm D. 6?cm
10.如图,梯子AB靠在墙上,梯子的底端A到墙根O的距离为2m,梯子的顶端B到地面的距离为7m,现将梯子的底端A向外移动到,使梯子的底端到墙根O的距离等于3m,同时梯子的顶端B下降至,那么
A. 小于1m
B. 大于1m
C. 等于1m
D. 小于或等于1m
二、填空题(本大题共10小题,共30.0分)
11.如果三角形的三边分别为,,2,那么这个三角形的最大角的度数为______.
12.一个三角形的三边的比是,它的周长是24,则它的面积是____________.
13.在中,点D为BC的中点,,,,则_________.
14.如图,在一个高为5m,长为13m的楼梯表面铺地毯,则地毯的长度至少是______.
15.已知甲、乙两人在同一地点出发,甲往东走4km,乙往南走了3km,这时甲、乙两人相距______km.
16.有一根7cm木棒,要放在长,宽,高分别为5cm,4cm,3cm的木箱中,______填“能”或“不能”放进去.
17.如图,在中,,,BC边上的中线,则的面积为______.
18.如图,为测量小区内池塘最宽处A、B两点间的距离,在池塘边定一点C,使,并测得AC的长18m,BC的长为30m,则最宽处AB的距离为______.
19.如图所示的一块地,,,,,,则这块地的面积为______ .
20.如图,某会展中心在会展期间准备将高5m,长13m,宽2m的楼道上铺地毯,已知地毯每平方米18元,请你帮助计算一下,铺完这个楼道至少需要______元钱.
三、解答题(本大题共4小题,共32.0分)
21.如图,在正方形网格中,小正方形的边长为1,A、B、C为格点格子线的交点
(1)判断的形状,并说明理由;
(2)求AB边上的高.
22.已知:如图,四边形ABCD中,,,,,,求四边形ABCD的面积.
23.如图,小刚想知道学校旗杆的高度,他发现旗杆顶端A处的绳子垂到地面B处后还多2米.当他把绳子拉直并使下端刚好接触到地面C处,发现绳子下端到旗杆下端的距离为6米,请你帮小刚求出旗杆的高度AB长.
24.一写字楼发生火灾,消防车立即赶到距大楼9米的点A处升起云梯到发生火灾的窗口点C处已知云梯BC长15米,云梯底部B距地面A为米问发生火灾的窗口C距地面有多少米
答案和解析
1.【答案】B
【解析】【分析】
本题考查勾股定理的逆定理的应用.判断三角形是否为直角三角形,已知三角形三边的长,只要利用勾股定理的逆定理加以判断即可.
由勾股定理的逆定理,只要验证两小边的平方和等于最长边的平方即可.
【解答】
解:A、,故不是直角三角形,故此选项错误;
B、,故是直角三角形,故此选项正确;
C、,故不是直角三角形,故此选项错误;
D、,故不是直角三角形,故此选项错误.
故选:B.
2.【答案】D
【解析】解:A、,此组数据不能作为直角三角形的三边长,故本选项错误;
B、,此组数据不能作为直角三角形的三边长,故本选项错误;
C、,此组数据不能作为直角三角形的三边长,故本选项错误;
D、,此组数据能作为直角三角形的三边长,故本选项正确.
故选:D.
根据勾股定理的逆定理对各选项进行逐一分析即可.
本题考查的是勾股定理的逆定理,熟知如果三角形的三边长a,b,c满足,那么这个三角形就是直角三角形是解答此题的关键.
3.【答案】A
【解析】【分析】
欲求证是否为直角三角形,这里给出三边的长,只要验证两小边的平方和等于最长边的平方即可.
本题考查勾股定理的逆定理的应用.判断三角形是否为直角三角形,已知三角形三边的长,只要利用勾股定理的逆定理加以判断即可.
【解答】
解:,故是直角三角形,故正确;
,故不是直角三角形,故错误;
,故不是直角三角形,故错误;
,故是直角三角形,正确.
故选A.
4.【答案】C
【解析】解::BC::4:5,
设,则,,
,
,
为直角三角形.
故选C.
根据勾股定理的逆定理求解即可.
本题考查勾股定理的逆定理,注意掌握勾股定理的逆定理:如果三角形的三边长a,b,c满足,那么这个三角形就是直角三角形.
5.【答案】D
【解析】【分析】
本题考查了勾股定理的逆定理,用到的知识点是绝对值、偶次方的性质、勾股定理的逆定理、完全平方公式,关键是证出a,b,c之间的关系.根据给出的条件求出三角形的三边长,再根据勾股定理的逆定理来判定三角形的形状.
【解答】
解:,
,
,,,
,
此三角形是直角三角形.
故选D.
6.【答案】D
【解析】解:在中,米,
故可得地毯长度米,
故选:D.
先求出AC的长,利用平移的知识可得出地毯的长度.
此题考查了勾股定理的应用及平移的知识,属于基础题,利用勾股定理求出AC的长度是解答本题的关键.
7.【答案】D
【解析】解:由勾股定理,得
路,
少走步,
故选:D.
根据勾股定理,可得答案.
本题考查了勾股定理,利用勾股定理得出路的长是解题关键.
8.【答案】D
【解析】【分析】
本题主要考查了勾股定理的知识点,善于观察题目的信息是解题以及学好数学的关键找到题中的直角三角形,芦苇离池边的水平距离为尺,设水深为x尺,根据勾股定理即可解答.
【解答】
解:设水深为x尺,则芦苇长为尺,
根据勾股定理得:,
解得:,
芦苇的长度尺,
故选D.
9.【答案】C
【解析】解:设,则,,
在中,,
即.
解得:.
故选:C.
在折叠的过程中,,从而设,即可表示AE,在直角三角形ADE中,根据勾股定理列方程即可求解.
此题主要考查了翻折变换的问题,解答本题的关键是掌握翻折前后对应线段相等,另外要熟练运用勾股定理解直角三角形.
10.【答案】A
【解析】【分析】
本题考查了勾股定理的应用,属于基础题,解答本题的关键是掌握勾股定理的表达式.由题意可知,,先利用勾股定理求出AB,梯子移动过程中长短不变,所以,又由题意可知,利用勾股定理分别求长,把其相减得解.
【解答】
解:在直角三角形AOB中,因为,,
由勾股定理得:,
由题意可知,
又,根据勾股定理得:,
.
故选A.
11.【答案】
【解析】【分析】
此题主要考查了勾股定理逆定理,关键是掌握判断一个三角形是不是直角三角形.必须满足较小两边平方的和等于最大边的平方才能做出判断.
根据勾股定理的逆定理:如果三角形的三边长a,b,c满足,那么这个三角形就是直角三角形可得答案.
【解答】
解:,
此三角形是直角三角形,
这个三角形的最大角的度数为,
故答案为:.
12.【答案】24
【解析】【分析】
本题考查的是勾股定理的逆定理,即如果三角形的三边长a,b,c满足,那么这个三角形就是直角三角形先根据三角形的三边长的比是3:4:5,它的周长是24求出三角形各边的长,再根据勾股定理的逆定理判断出其形状,由三角形的面积公式即可求解.
【解答】
解:三角形的三边长的比是3:4:5,它的周长是24,
设此三角形的边长分别是3x,4x,5x,则,解得,
此三角形的边长分别是6,8,10,
,
此三角形是直角三角形,
这个三角形的面积?
故答案为
13.【答案】5
【解析】【分析】
本题考查的是勾股定理,勾股定理逆定理有关知识,根据BD,AD,AB的长度可以判定为直角三角形,即,又由于D为BC的中点,可以判定为等腰三角形,且.
【解答】
解:如图:
在中,已知,,,满足,
是直角三角形,即,
又为BC的中点,
为等腰三角形,且,
.
故答案为
14.【答案】17m
【解析】解:由勾股定理得:
楼梯的水平宽度,
地毯铺满楼梯是其长度的和应该是楼梯的水平宽度与垂直高度的和,
地毯的长度至少是米.
故答案为:17m.
当地毯铺满楼梯时其长度的和应该是楼梯的水平宽度与垂直高度的和,根据勾股定理求得水平宽度,然后求得地毯的长度即可.
本题考查了勾股定理的知识,与实际生活相联系,加深了学生学习数学的积极性.
15.【答案】5
【解析】解:如图,
,,
.
因为甲向东走,乙向南走,其刚好构成一个直角.两人走的距离分别是两直角边,则根据勾股定理可求得斜边即两人的距离.
此题主要考查学生对勾股定理的理解及实际生活中的运用.
16.【答案】能
【解析】解:此长方体木箱的对角线长为,
木棒能放进去.
故答案为:能.
根据此长方体木箱的对角线的长与木棒的长比较以确定能不能放入.
本题考查了勾股定理在实际生活中的运用.
17.【答案】24
【解析】【分析】
本题考查的是勾股定理及逆定理,以及全等三角形的判定与性质,熟练掌握勾股定理的逆定理是解题的关键.延长AD到E,使,连接CE,利用SAS得出与全等,得到,利用勾股定理的逆定理得到为直角三角形,的面积等于的面积,利用三角形的面积公式即可得出结果.
【解答】
解:延长AD到E,使,连接CE,如图所示:
为BC的中点,
,
在与中,,
≌,
.
又,,,
,
,
则;
故答案为:24.
18.【答案】24m
【解析】解:中,,,,
.
故答案为:24m.
直接根据勾股定理求解即可.
本题考查的是勾股定理的应用,熟知勾股定理是解答此题的关键.
19.【答案】216
【解析】解:连接AC,则在中,
,
,在中,,
,
,
,
平方米,
故答案为:216.
连接AC,运用勾股定理逆定理可证,为直角三角形,可求出两直角三角形的面积,此块地的面积为两个直角三角形的面积差.
本题考查了勾股定理和三角形面积的应用,注意:在直角三角形中.两直角边的平方和等于斜边的平方.
20.【答案】612
【解析】解:由勾股定理,.
则地毯总长为,
则地毯的总面积为平方米,
所以铺完这个楼道至少需要元.
故答案为:612.
地毯的长是楼梯的竖直部分与水平部分的和,即AC与BC的和,在直角中,根据勾股定理即可求得BC的长,地毯的长与宽的积就是面积.
本题考查了勾股定理的应用,正确理解地毯的长度的计算是解题的关键.
21.【答案】解:,,,
,
是直角三角形;
设AB边上的高为h,
,
.
即AB边上的高为.
【解析】根据勾股定理和勾股定理的逆定理即可得到结论;
根据三角形的面积公式即可得到结论.
本题考查了勾股定理和勾股定理的逆定理,熟练掌握勾股定理是解题的关键.
22.【答案】解:连结AC,
在中,
,,,
,
,
在中,
,,,
,
是直角三角形,
?
四边形ABCD的面积.
【解析】连接AC,根据勾股定理求出AC,根据勾股定理的逆定理求出是直角三角形,分别求出和的面积,即可得出答案.
本题考查了勾股定理,勾股定理的逆定理的应用,解此题的关键是能求出和的面积,注意:如果一个三角形的两边的平方和等于第三边的平方,那么这个三角形是直角三角形.
23.【答案】解:设旗杆的高度为x米,则绳子的长度为米,
根据勾股定理可得:,
解得,.
答:旗杆的高度为8米.
【解析】因为旗杆、绳子、地面正好构成直角三角形,设旗杆的高度为x米,则绳子的长度为米,根据勾股定理即可求得旗杆的高度.
此题考查了学生利用勾股定理解决实际问题的能力,解答本题的关键是用未知数表示出三边长度,利用勾股定理解答.
24.【答案】解:由题意可得:
米,米,
为直角三角形,且,
,
则,
答:发生火灾的窗口距地面有米.
【解析】此题主要考查了勾股定理的应用,得出DC的长是解题关键.利用勾股定理得出DC的长,进而求出HC的长.
第2页,共2页
第1页,共1页
