北师大版七年级数学下册 第5章 生活中的轴对称 单元测试题(有答案)
文档属性
| 名称 | 北师大版七年级数学下册 第5章 生活中的轴对称 单元测试题(有答案) |  | |
| 格式 | zip | ||
| 文件大小 | 278.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-02-12 11:53:07 | ||
图片预览



文档简介
北师大版七年级数学下册 第5章 生活中的轴对称 单元测试题
一.选择题(共10小题)
1.下列交通标志图案是轴对称图形的是( )
A. B. C. D.
2.△ABC中,AB=BC=6,∠B=60°,则AC等于( )
A.4 B.6 C.8 D.10
3.如图,△ABC是等边三角形,点D在AC边上,∠DBC=35°,则∠ADB的度数为( )
A.25° B.60° C.85° D.95°
4.如图,若∠2=30°,为了使白球反弹后能将黑球直接撞入袋中,那么击打白球时,必须保证∠1的度数为( )
A.15° B.30° C.45° D.60°
5.如图,已知∠O,点P为其内一定点,分别在∠O的两边上找点A、B,使△PAB周长最小的是( )
A. B.
C. D.
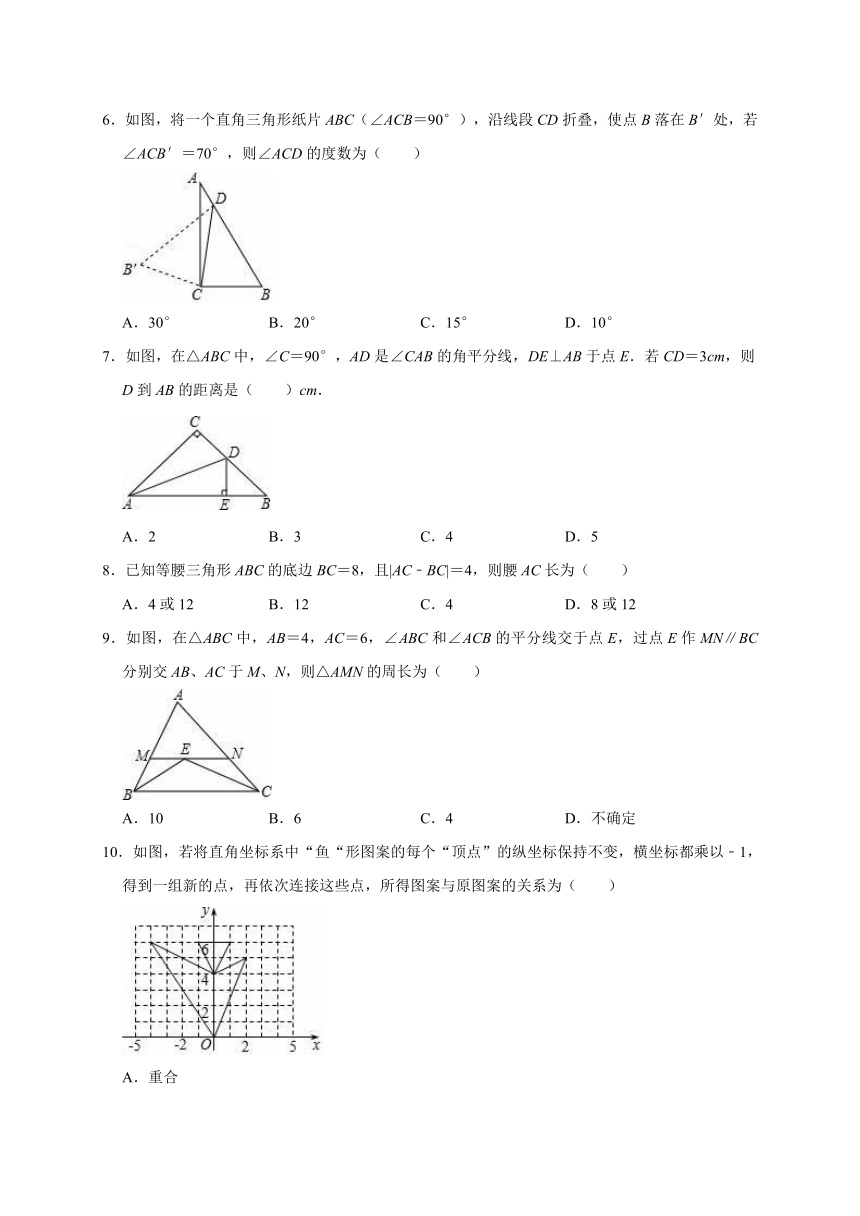
6.如图,将一个直角三角形纸片ABC(∠ACB=90°),沿线段CD折叠,使点B落在B′处,若∠ACB′=70°,则∠ACD的度数为( )
A.30° B.20° C.15° D.10°
7.如图,在△ABC中,∠C=90°,AD是∠CAB的角平分线,DE⊥AB于点E.若CD=3cm,则D到AB的距离是( )cm.
A.2 B.3 C.4 D.5
8.已知等腰三角形ABC的底边BC=8,且|AC﹣BC|=4,则腰AC长为( )
A.4或12 B.12 C.4 D.8或12
9.如图,在△ABC中,AB=4,AC=6,∠ABC和∠ACB的平分线交于点E,过点E作MN∥BC分别交AB、AC于M、N,则△AMN的周长为( )
A.10 B.6 C.4 D.不确定
10.如图,若将直角坐标系中“鱼“形图案的每个“顶点”的纵坐标保持不变,横坐标都乘以﹣1,得到一组新的点,再依次连接这些点,所得图案与原图案的关系为( )
A.重合
B.关于x轴对称
C.关于y轴对称
D.宽度不变,高度变为原来的一半
二.填空题(共8小题)
11.如图,在△ABC中,AB=AC,D,E是△ABC内两点,AD平分∠BAC,∠EBC=∠E=60°,若BE=9cm,DE=3cm,则BC= cm.
12.如图已知OA=a,P是射线ON上一动点,∠AON=60°,当OP= 时,△AOP为等边三角形.
13.如图,在△ABC中,已知AD是∠BAC的平分线,DE∥AB,交AC于点E,AB=15,AC=10,则CE= .
14.在△ABC中,AB=AC,∠BAC>90°,点E在边BC上,且使△ABE和△ACE都为等腰三角形,则∠EAC= 度.
15.如图,在△ABC中,∠ACB=90°,AD是△ABC的角平分线,BC=10cm,BD:DC=3:2,则点D到AB的距离为 .
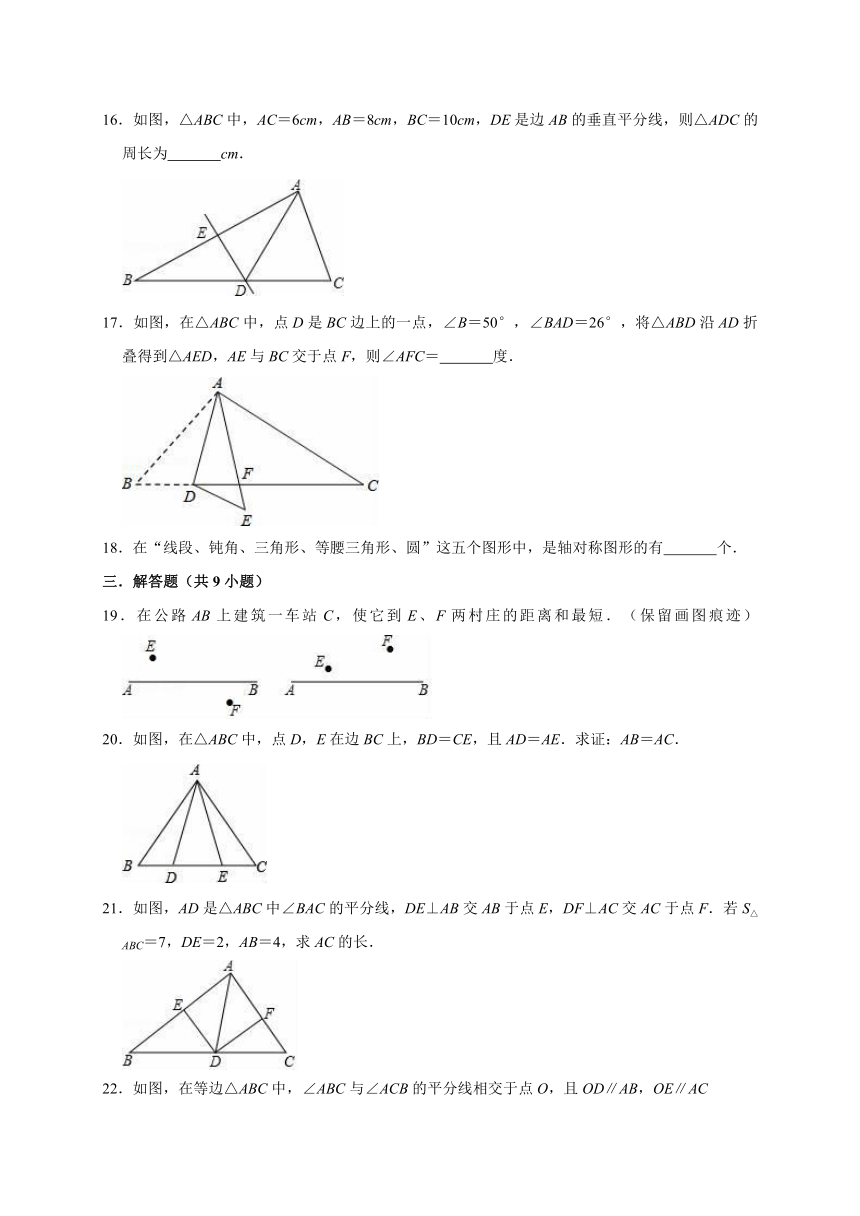
16.如图,△ABC中,AC=6cm,AB=8cm,BC=10cm,DE是边AB的垂直平分线,则△ADC的周长为 cm.
17.如图,在△ABC中,点D是BC边上的一点,∠B=50°,∠BAD=26°,将△ABD沿AD折叠得到△AED,AE与BC交于点F,则∠AFC= 度.
18.在“线段、钝角、三角形、等腰三角形、圆”这五个图形中,是轴对称图形的有 个.
三.解答题(共9小题)
19.在公路AB上建筑一车站C,使它到E、F两村庄的距离和最短.(保留画图痕迹)
20.如图,在△ABC中,点D,E在边BC上,BD=CE,且AD=AE.求证:AB=AC.
21.如图,AD是△ABC中∠BAC的平分线,DE⊥AB交AB于点E,DF⊥AC交AC于点F.若S△ABC=7,DE=2,AB=4,求AC的长.
22.如图,在等边△ABC中,∠ABC与∠ACB的平分线相交于点O,且OD∥AB,OE∥AC
(1)试判定△ODE的形状,并说明你的理由;
(2)若BC=10,求△ODE的周长.
23.如图,△ABC中,∠ACB=90°,将△ABC沿着一条直线折叠后,使点A与点C重合(如图②)
(1)在图①中画出折痕所在的直线l,问直线l是线段AC的 线;
(2)设直线l与AB、AC分别相交于点M、N,连结CM,若△CMB的周长是21cm,AB=14cm,求BC的长.
24.如图,在△ABC中,边AB、AC的垂直平分线分别交BC于D、E.
(1)若BC=5,求△ADE的周长.
(2)若∠BAD+∠CAE=60°,求∠BAC的度数.
25.在平面直角坐标系中,△ABC的三个顶点的位置如图所示
(1)请画出△ABC关于y轴对称的△A′B′C′;(其中A′、B′、C′分别是A、B、C的对应点,不写画法)
(2)直接写出A′B′C′三点的坐标;
(3)求△ABC的面积.
26.如图,△ABC中,AE=BE,∠AED=∠ABC.
(1)求证:BD平分∠ABC;
(2)若AB=CB,∠AED=4∠EAD,求∠C的度数.
27.在△ABC中,AB=AC,∠ABC、∠ACB的平分线交于O点,过O点作EF∥BC交AB、AC于E、F.
(1)如图1,图中所有的等腰三角形有 个.猜想:EF与BE、CF之间有怎样的关系,并说明理由.
(2)如图2,AB≠AC,图中等腰三角形是 ,(1)中的EF与BE、CF之间的关系还存在吗?
(3)如图3,△ABC中∠ABC的平分线BO与三角形外角平分线CO交于O,过O点作OE∥BC交AB于E,交AC于F.图中还有等腰三角形吗?如果有,分别指出它们,写出EF与BE、CF关系,并说明理由.
参考答案与试题解析
一.选择题(共10小题)
1.解:A、不是轴对称图形,故本选项错误;
B、是轴对称图形,故本选项正确;
C、不是轴对称图形,故本选项错误;
D、不是轴对称图形,故本选项错误.
故选:B.
2.解:∵在△ABC中,AB=BC=6,∠B=60°,
∴△ABC是等边三角形,
∴AC=6.
故选:B.
3.解:∠ADB=∠DBC+∠C=35°+60°=95°.
故选:D.
4.解:要使黑球反弹后能将黑球直接撞入袋中,
∠2+∠3=90°,
∵∠2=30°,
∴∠3=60°,
∴∠1=60°.
故选:D.
5.解:分别在∠O的两边上找点A、B,使△PAB周长最小的是D选项,
故选:D.
6.解:∵∠B'CB=∠ACB+∠ACB'
∴∠B'CB=160°
∵折叠
∴∠B'CD=∠BCD=∠B'CB=80°
∴∠ACD=∠ACB﹣∠BCD=10°
故选:D.
7.解:∵AD是∠CAB的角平分线,DE⊥AB,∠C=90°,
∴DE=CD=3,
故选:B.
8.解:∵|AC﹣BC|=4,
∴AC﹣BC=±4,
∵等腰△ABC的底边BC=8,
∴AC=12.AC=4(不合题意舍去),
故选:B.
9.解:∵MN∥BC,
∴∠AMN=∠ABC.
∵BE平分∠ABC,
∴∠ABC=2∠MBE,
∴∠AMN=2∠MBE.
∵∠AMN=∠MBE+∠MEB,
∴∠MBE=∠MEB,
∴MB=ME.
同理,NC=NE,
∴C△AMN=AM+ME+EN+AN=AB+AC=10.
故选:A.
10.解:图案的每个“顶点”的纵坐标保持不变,横坐标分别乘﹣1,
则对应点的横坐标互为相反数,纵坐标相同,
所以,所得图案与原图案关于y轴对称.
故选:C.
二.填空题(共8小题)
11.解;过点E作EF⊥BC,垂足为F,延长AD到H,交BC于点H,过点D作DG⊥EF,垂足为G.
∵EF⊥BC,∠EBF=60°,
∴∠BEF=30°,
∴BF=,
∵∠BED=60°,∠BEF=30°,
∴∠DEG=30°.
又∵DG⊥EF,
∴GD=,
∵AB=AC,AD平分∠BAC,
∴AH⊥BC,且BH=CH.
∵AH⊥BC,EF⊥BC,DG⊥EF,
∴四边形DGFH是矩形.
∴FH=GD=1.5.
∴BC=2BH=2×(4.5+1.5)=12.
故答案为:12.
12.解:∵AON=60°,
∴当OA=OP=a时,△AOP为等边三角形.
故答案是:a.
13.解:∵AD是∠BAC的平分线,
∴∠CAD=∠BAD,
∵DE∥AB,
∴∠EDA=∠BAD,
∴∠EDA=∠CAD,
∴ED=AE,
设AE=x,则ED=x,CE=10﹣x,
∵ED∥AB,
∴,
∴,
∴x=6,
∴CE=10﹣6=4,
故答案为:4.
14.解:如图1中,当EB=EA,CA=CE时,
∴∠B=∠BAE,∠CEA=∠CAE,
设∠B=∠BAE=x,则∠AEC=∠CAE=2x,
∵AB=AC,
∴∠B=∠C=x,
∵∠CEA+∠CAE+∠C=180°,
∴5x=180°,
∴x=36°,
∴∠EAC=72°,
如图2中,当BA=BE,EA=EC时,同法可得∠EAC=36°,
故答案为36和72.
15.解:∵BC=10cm,BD:DC=3:2,
∴DC=4cm,
∵AD是△ABC的角平分线,∠ACB=90°,
∴点D到AB的距离等于DC,即点D到AB的距离等于4cm.
故答案为4cm.
16.解:∵DE是边AB的垂直平分线,BC=10cm,AC=6cm,
∴AD=BD,
∴△ADC的周长=AD+DC+AC=BD+DC+AC=BC+AC=16cm;
故答案为:16.
17.解:∵将△ABD沿AD折叠得到△AED,
∴∠BAD=∠DAF=26°,
∴∠BAF=52°,
∵∠B+∠BAF+∠AFB=180°,
∴∠AFB=78°,
∴∠AFC=102°,
故答案为:102.
18.解:根据轴对称图形的定义可知:
线段、钝角、等腰三角形和圆都是轴对称图形.
故答案为:4.
三.解答题(共9小题)
19.解:①连接EF交AB于点C,点C就是所求的点;
②画出点E关于直线AB的对称点E′,连接E′F交AB于点C,连接EC,
∵E、E′关于直线AB对称,
∴EC=E′C,
∴EC+FC=E′F,
由两点之间线段最短可知,线段E′F的长即为EC+FC的最小值,故C点即为所求点.
20.证明:作AF⊥BC于点F,
∵AD=AE,
∴DF=EF,
∵BD=CE,
∴BD+DF=CE+EF,
即 BF=CF,
∵AF⊥BC,
∴AB=AC.
21.解:∵AD是△ABC中∠BAC的平分线,DE⊥AB于点E,DF⊥AC交AC于点F,
∴DF=DE=2.
又∵S△ABC=S△ABD+S△ACD,AB=4,
∴7=×4×2+×AC×2,
∴AC=3.
22.解:(1)△ODE是等边三角形;理由如下:
∵△ABC是等边三角形,
∴∠ABC=∠ACB=60°;
∵OD∥AB,OE∥AC,
∴∠ODE=∠ABC=60°,∠OED=∠ACB=60°,
∴△ODE为等边三角形.
(2)∵OB平分∠ABC,OD∥AB,
∴∠ABO=∠DOB,∠ABO=∠DBO,
∴∠DOB=∠DBO,
∴BD=OD;同理可证CE=OE;
∴△ODE的周长=BC=10.
23.解:(1)如图①,
∵将△ABC沿着一条直线折叠后,使点A与点C重合,
∴AN=NC,∠ANM=∠CNM=90°,
∴直线l是线段AC的中垂线,
故答案为:中垂;
(2)∵将△ABC沿着一条直线折叠后,使点A与点C重合,
∴AM=CM,
∵△CMB的周长是21cm,AB=14cm,
∴21=CM+BM+BC=AM+BM+CB=AB+BC=14+BC,
∴BC=7cm.
24.解:(1)∵边AB、AC的垂直平分线分别交BC于D、E,
∴DA=DB,EA=EC,
∴△ADE的周长=AD+DE+AE=DB+DE+EC=BC=5;
(2)∵DA=DB,EA=EC,
∴∠DAB=∠B,∠EAC=∠C,
∴∠B+∠C=∠DAB+∠EAC=60°,
∴∠BAC=120°.
25.解:(1)如图,△A′B′C′;
(2)A′(2,3),B′(3,1),C′(﹣1,﹣2);
(3)△ABC的面积=4×5﹣×3×4﹣×2×1﹣×5×3=5.5.
26.(1)证明:∵∠AED=∠ABC,∠AED=∠ABE+∠EAB,∠ABC=∠ABE+∠DBC,
∴∠EAB=∠DBC,
∵AE=BE,
∴∠EAB=∠ABE,
∴∠DBC=∠ABE,
∴BD平分∠ABC;
(2)设∠EAD=x,则∠AED=4x,
∵∠AED=∠ABE+∠EAB,∠EAB=∠ABE,BD平分∠ABC,
∴∠BAE=2x,∠ABC=4x,
∴∠BAC=3x,
∵AB=CB,
∴∠BAC=∠C,
∴∠C=3x,
∵∠ABC+∠BAC+∠C﹣180°,
∴4x+3x+3x=180°,
解得,x=18°,
∴∠C=3x=54°,
即∠C的度数是54°.
27.解:(1)图中是等腰三角形的有:△AEF、△OEB、△OFC、△OBC、△ABC共5个;
EF、BE、FC的关系是EF=BE+FC.
理由如下:
∵OB、OC平分∠ABC、∠ACB,
∴∠ABO=∠OBC,∠ACO=∠OCB,
∵EF∥BC,
∴∠EOB=∠OBC=∠EBO,∠FOC=∠OCB=∠FCO,
即EO=EB,FO=FC,
∴EF=EO+OF=BE+CF;
故答案为:5;
(2)当AB≠AC时,△EOB、△FOC仍为等腰三角形,(1)的结论仍然成立,
∵OB、OC平分∠ABC、∠ACB,
∴∠ABO=∠OBC,∠ACO=∠OCB,
∵EF∥BC,
∴∠EOB=∠OBC=∠EBO,∠FOC=∠OCB=∠FCO,
即EO=EB,FO=FC,
∴EF=EO+OF=BE+CF;
故答案为:△EOB、△FOC;
(3)△EOB和△FOC仍是等腰三角形,EF=BE﹣FC.理由如下:
同(1)可证得△EOB是等腰三角形;
∵EO∥BC,
∴∠FOC=∠OCG;
∵OC平分∠ACG,
∴∠ACO=∠FOC=∠OCG,
∴FO=FC,故△FOC是等腰三角形;
∴EF=EO﹣FO=BE﹣FC.
一.选择题(共10小题)
1.下列交通标志图案是轴对称图形的是( )
A. B. C. D.
2.△ABC中,AB=BC=6,∠B=60°,则AC等于( )
A.4 B.6 C.8 D.10
3.如图,△ABC是等边三角形,点D在AC边上,∠DBC=35°,则∠ADB的度数为( )
A.25° B.60° C.85° D.95°
4.如图,若∠2=30°,为了使白球反弹后能将黑球直接撞入袋中,那么击打白球时,必须保证∠1的度数为( )
A.15° B.30° C.45° D.60°
5.如图,已知∠O,点P为其内一定点,分别在∠O的两边上找点A、B,使△PAB周长最小的是( )
A. B.
C. D.
6.如图,将一个直角三角形纸片ABC(∠ACB=90°),沿线段CD折叠,使点B落在B′处,若∠ACB′=70°,则∠ACD的度数为( )
A.30° B.20° C.15° D.10°
7.如图,在△ABC中,∠C=90°,AD是∠CAB的角平分线,DE⊥AB于点E.若CD=3cm,则D到AB的距离是( )cm.
A.2 B.3 C.4 D.5
8.已知等腰三角形ABC的底边BC=8,且|AC﹣BC|=4,则腰AC长为( )
A.4或12 B.12 C.4 D.8或12
9.如图,在△ABC中,AB=4,AC=6,∠ABC和∠ACB的平分线交于点E,过点E作MN∥BC分别交AB、AC于M、N,则△AMN的周长为( )
A.10 B.6 C.4 D.不确定
10.如图,若将直角坐标系中“鱼“形图案的每个“顶点”的纵坐标保持不变,横坐标都乘以﹣1,得到一组新的点,再依次连接这些点,所得图案与原图案的关系为( )
A.重合
B.关于x轴对称
C.关于y轴对称
D.宽度不变,高度变为原来的一半
二.填空题(共8小题)
11.如图,在△ABC中,AB=AC,D,E是△ABC内两点,AD平分∠BAC,∠EBC=∠E=60°,若BE=9cm,DE=3cm,则BC= cm.
12.如图已知OA=a,P是射线ON上一动点,∠AON=60°,当OP= 时,△AOP为等边三角形.
13.如图,在△ABC中,已知AD是∠BAC的平分线,DE∥AB,交AC于点E,AB=15,AC=10,则CE= .
14.在△ABC中,AB=AC,∠BAC>90°,点E在边BC上,且使△ABE和△ACE都为等腰三角形,则∠EAC= 度.
15.如图,在△ABC中,∠ACB=90°,AD是△ABC的角平分线,BC=10cm,BD:DC=3:2,则点D到AB的距离为 .
16.如图,△ABC中,AC=6cm,AB=8cm,BC=10cm,DE是边AB的垂直平分线,则△ADC的周长为 cm.
17.如图,在△ABC中,点D是BC边上的一点,∠B=50°,∠BAD=26°,将△ABD沿AD折叠得到△AED,AE与BC交于点F,则∠AFC= 度.
18.在“线段、钝角、三角形、等腰三角形、圆”这五个图形中,是轴对称图形的有 个.
三.解答题(共9小题)
19.在公路AB上建筑一车站C,使它到E、F两村庄的距离和最短.(保留画图痕迹)
20.如图,在△ABC中,点D,E在边BC上,BD=CE,且AD=AE.求证:AB=AC.
21.如图,AD是△ABC中∠BAC的平分线,DE⊥AB交AB于点E,DF⊥AC交AC于点F.若S△ABC=7,DE=2,AB=4,求AC的长.
22.如图,在等边△ABC中,∠ABC与∠ACB的平分线相交于点O,且OD∥AB,OE∥AC
(1)试判定△ODE的形状,并说明你的理由;
(2)若BC=10,求△ODE的周长.
23.如图,△ABC中,∠ACB=90°,将△ABC沿着一条直线折叠后,使点A与点C重合(如图②)
(1)在图①中画出折痕所在的直线l,问直线l是线段AC的 线;
(2)设直线l与AB、AC分别相交于点M、N,连结CM,若△CMB的周长是21cm,AB=14cm,求BC的长.
24.如图,在△ABC中,边AB、AC的垂直平分线分别交BC于D、E.
(1)若BC=5,求△ADE的周长.
(2)若∠BAD+∠CAE=60°,求∠BAC的度数.
25.在平面直角坐标系中,△ABC的三个顶点的位置如图所示
(1)请画出△ABC关于y轴对称的△A′B′C′;(其中A′、B′、C′分别是A、B、C的对应点,不写画法)
(2)直接写出A′B′C′三点的坐标;
(3)求△ABC的面积.
26.如图,△ABC中,AE=BE,∠AED=∠ABC.
(1)求证:BD平分∠ABC;
(2)若AB=CB,∠AED=4∠EAD,求∠C的度数.
27.在△ABC中,AB=AC,∠ABC、∠ACB的平分线交于O点,过O点作EF∥BC交AB、AC于E、F.
(1)如图1,图中所有的等腰三角形有 个.猜想:EF与BE、CF之间有怎样的关系,并说明理由.
(2)如图2,AB≠AC,图中等腰三角形是 ,(1)中的EF与BE、CF之间的关系还存在吗?
(3)如图3,△ABC中∠ABC的平分线BO与三角形外角平分线CO交于O,过O点作OE∥BC交AB于E,交AC于F.图中还有等腰三角形吗?如果有,分别指出它们,写出EF与BE、CF关系,并说明理由.
参考答案与试题解析
一.选择题(共10小题)
1.解:A、不是轴对称图形,故本选项错误;
B、是轴对称图形,故本选项正确;
C、不是轴对称图形,故本选项错误;
D、不是轴对称图形,故本选项错误.
故选:B.
2.解:∵在△ABC中,AB=BC=6,∠B=60°,
∴△ABC是等边三角形,
∴AC=6.
故选:B.
3.解:∠ADB=∠DBC+∠C=35°+60°=95°.
故选:D.
4.解:要使黑球反弹后能将黑球直接撞入袋中,
∠2+∠3=90°,
∵∠2=30°,
∴∠3=60°,
∴∠1=60°.
故选:D.
5.解:分别在∠O的两边上找点A、B,使△PAB周长最小的是D选项,
故选:D.
6.解:∵∠B'CB=∠ACB+∠ACB'
∴∠B'CB=160°
∵折叠
∴∠B'CD=∠BCD=∠B'CB=80°
∴∠ACD=∠ACB﹣∠BCD=10°
故选:D.
7.解:∵AD是∠CAB的角平分线,DE⊥AB,∠C=90°,
∴DE=CD=3,
故选:B.
8.解:∵|AC﹣BC|=4,
∴AC﹣BC=±4,
∵等腰△ABC的底边BC=8,
∴AC=12.AC=4(不合题意舍去),
故选:B.
9.解:∵MN∥BC,
∴∠AMN=∠ABC.
∵BE平分∠ABC,
∴∠ABC=2∠MBE,
∴∠AMN=2∠MBE.
∵∠AMN=∠MBE+∠MEB,
∴∠MBE=∠MEB,
∴MB=ME.
同理,NC=NE,
∴C△AMN=AM+ME+EN+AN=AB+AC=10.
故选:A.
10.解:图案的每个“顶点”的纵坐标保持不变,横坐标分别乘﹣1,
则对应点的横坐标互为相反数,纵坐标相同,
所以,所得图案与原图案关于y轴对称.
故选:C.
二.填空题(共8小题)
11.解;过点E作EF⊥BC,垂足为F,延长AD到H,交BC于点H,过点D作DG⊥EF,垂足为G.
∵EF⊥BC,∠EBF=60°,
∴∠BEF=30°,
∴BF=,
∵∠BED=60°,∠BEF=30°,
∴∠DEG=30°.
又∵DG⊥EF,
∴GD=,
∵AB=AC,AD平分∠BAC,
∴AH⊥BC,且BH=CH.
∵AH⊥BC,EF⊥BC,DG⊥EF,
∴四边形DGFH是矩形.
∴FH=GD=1.5.
∴BC=2BH=2×(4.5+1.5)=12.
故答案为:12.
12.解:∵AON=60°,
∴当OA=OP=a时,△AOP为等边三角形.
故答案是:a.
13.解:∵AD是∠BAC的平分线,
∴∠CAD=∠BAD,
∵DE∥AB,
∴∠EDA=∠BAD,
∴∠EDA=∠CAD,
∴ED=AE,
设AE=x,则ED=x,CE=10﹣x,
∵ED∥AB,
∴,
∴,
∴x=6,
∴CE=10﹣6=4,
故答案为:4.
14.解:如图1中,当EB=EA,CA=CE时,
∴∠B=∠BAE,∠CEA=∠CAE,
设∠B=∠BAE=x,则∠AEC=∠CAE=2x,
∵AB=AC,
∴∠B=∠C=x,
∵∠CEA+∠CAE+∠C=180°,
∴5x=180°,
∴x=36°,
∴∠EAC=72°,
如图2中,当BA=BE,EA=EC时,同法可得∠EAC=36°,
故答案为36和72.
15.解:∵BC=10cm,BD:DC=3:2,
∴DC=4cm,
∵AD是△ABC的角平分线,∠ACB=90°,
∴点D到AB的距离等于DC,即点D到AB的距离等于4cm.
故答案为4cm.
16.解:∵DE是边AB的垂直平分线,BC=10cm,AC=6cm,
∴AD=BD,
∴△ADC的周长=AD+DC+AC=BD+DC+AC=BC+AC=16cm;
故答案为:16.
17.解:∵将△ABD沿AD折叠得到△AED,
∴∠BAD=∠DAF=26°,
∴∠BAF=52°,
∵∠B+∠BAF+∠AFB=180°,
∴∠AFB=78°,
∴∠AFC=102°,
故答案为:102.
18.解:根据轴对称图形的定义可知:
线段、钝角、等腰三角形和圆都是轴对称图形.
故答案为:4.
三.解答题(共9小题)
19.解:①连接EF交AB于点C,点C就是所求的点;
②画出点E关于直线AB的对称点E′,连接E′F交AB于点C,连接EC,
∵E、E′关于直线AB对称,
∴EC=E′C,
∴EC+FC=E′F,
由两点之间线段最短可知,线段E′F的长即为EC+FC的最小值,故C点即为所求点.
20.证明:作AF⊥BC于点F,
∵AD=AE,
∴DF=EF,
∵BD=CE,
∴BD+DF=CE+EF,
即 BF=CF,
∵AF⊥BC,
∴AB=AC.
21.解:∵AD是△ABC中∠BAC的平分线,DE⊥AB于点E,DF⊥AC交AC于点F,
∴DF=DE=2.
又∵S△ABC=S△ABD+S△ACD,AB=4,
∴7=×4×2+×AC×2,
∴AC=3.
22.解:(1)△ODE是等边三角形;理由如下:
∵△ABC是等边三角形,
∴∠ABC=∠ACB=60°;
∵OD∥AB,OE∥AC,
∴∠ODE=∠ABC=60°,∠OED=∠ACB=60°,
∴△ODE为等边三角形.
(2)∵OB平分∠ABC,OD∥AB,
∴∠ABO=∠DOB,∠ABO=∠DBO,
∴∠DOB=∠DBO,
∴BD=OD;同理可证CE=OE;
∴△ODE的周长=BC=10.
23.解:(1)如图①,
∵将△ABC沿着一条直线折叠后,使点A与点C重合,
∴AN=NC,∠ANM=∠CNM=90°,
∴直线l是线段AC的中垂线,
故答案为:中垂;
(2)∵将△ABC沿着一条直线折叠后,使点A与点C重合,
∴AM=CM,
∵△CMB的周长是21cm,AB=14cm,
∴21=CM+BM+BC=AM+BM+CB=AB+BC=14+BC,
∴BC=7cm.
24.解:(1)∵边AB、AC的垂直平分线分别交BC于D、E,
∴DA=DB,EA=EC,
∴△ADE的周长=AD+DE+AE=DB+DE+EC=BC=5;
(2)∵DA=DB,EA=EC,
∴∠DAB=∠B,∠EAC=∠C,
∴∠B+∠C=∠DAB+∠EAC=60°,
∴∠BAC=120°.
25.解:(1)如图,△A′B′C′;
(2)A′(2,3),B′(3,1),C′(﹣1,﹣2);
(3)△ABC的面积=4×5﹣×3×4﹣×2×1﹣×5×3=5.5.
26.(1)证明:∵∠AED=∠ABC,∠AED=∠ABE+∠EAB,∠ABC=∠ABE+∠DBC,
∴∠EAB=∠DBC,
∵AE=BE,
∴∠EAB=∠ABE,
∴∠DBC=∠ABE,
∴BD平分∠ABC;
(2)设∠EAD=x,则∠AED=4x,
∵∠AED=∠ABE+∠EAB,∠EAB=∠ABE,BD平分∠ABC,
∴∠BAE=2x,∠ABC=4x,
∴∠BAC=3x,
∵AB=CB,
∴∠BAC=∠C,
∴∠C=3x,
∵∠ABC+∠BAC+∠C﹣180°,
∴4x+3x+3x=180°,
解得,x=18°,
∴∠C=3x=54°,
即∠C的度数是54°.
27.解:(1)图中是等腰三角形的有:△AEF、△OEB、△OFC、△OBC、△ABC共5个;
EF、BE、FC的关系是EF=BE+FC.
理由如下:
∵OB、OC平分∠ABC、∠ACB,
∴∠ABO=∠OBC,∠ACO=∠OCB,
∵EF∥BC,
∴∠EOB=∠OBC=∠EBO,∠FOC=∠OCB=∠FCO,
即EO=EB,FO=FC,
∴EF=EO+OF=BE+CF;
故答案为:5;
(2)当AB≠AC时,△EOB、△FOC仍为等腰三角形,(1)的结论仍然成立,
∵OB、OC平分∠ABC、∠ACB,
∴∠ABO=∠OBC,∠ACO=∠OCB,
∵EF∥BC,
∴∠EOB=∠OBC=∠EBO,∠FOC=∠OCB=∠FCO,
即EO=EB,FO=FC,
∴EF=EO+OF=BE+CF;
故答案为:△EOB、△FOC;
(3)△EOB和△FOC仍是等腰三角形,EF=BE﹣FC.理由如下:
同(1)可证得△EOB是等腰三角形;
∵EO∥BC,
∴∠FOC=∠OCG;
∵OC平分∠ACG,
∴∠ACO=∠FOC=∠OCG,
∴FO=FC,故△FOC是等腰三角形;
∴EF=EO﹣FO=BE﹣FC.
同课章节目录
- 第一章 整式的乘除
- 1 同底数幂的乘法
- 2 幂的乘方与积的乘方
- 3 同底数幂的除法
- 4 整式的乘法
- 5 平方差公式
- 6 完全平方公式
- 7 整式的除法
- 第二章 相交线与平行线
- 1 两条直线的位置关系
- 2 探索直线平行的条件
- 3 平行线的性质
- 4 用尺规作角
- 第三章 变量之间的关系
- 1 用表格表示的变量间关系
- 2 用关系式表示的变量间关系
- 3 用图象表示的变量间关系
- 第四章 三角形
- 1 认识三角形
- 2 图形的全等
- 3 探索三角形全等的条件
- 4 用尺规作三角形
- 5 利用三角形全等测距离
- 第五章 生活中的轴对称
- 1 轴对称现象
- 2 探索轴对称的性质
- 3 简单的轴对称图形
- 4 利用轴对称进行设计
- 第六章 概率初步
- 1 感受可能性
- 2 频率的稳定性
- 3 等可能事件的概率
