人教版八年级数学下册 17.1 勾股定理 同步练习(含答案)
文档属性
| 名称 | 人教版八年级数学下册 17.1 勾股定理 同步练习(含答案) |  | |
| 格式 | zip | ||
| 文件大小 | 71.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-02-12 13:40:02 | ||
图片预览

文档简介
勾股定理 同步练习
选择题
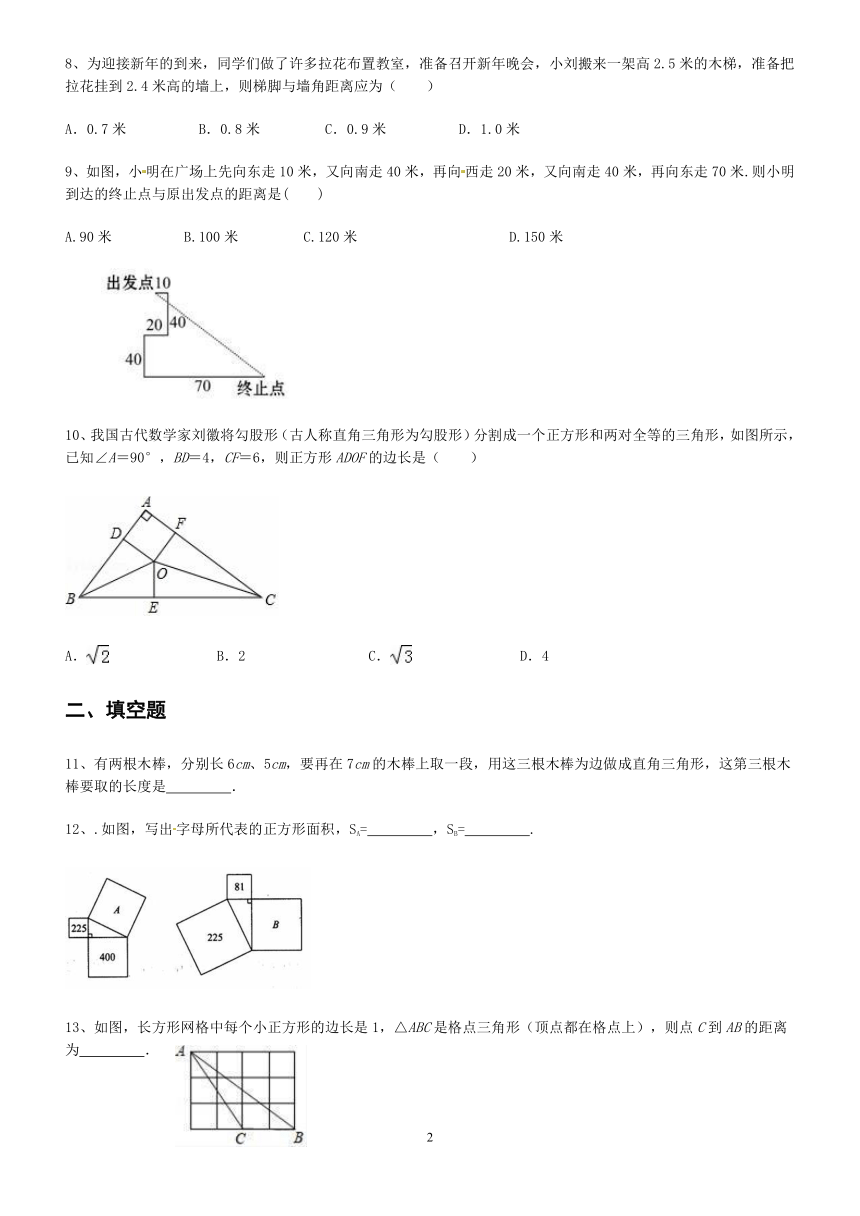
1、如图,数轴上点A对应的数是0,点B对应的数是1,BC⊥AB,垂足为B,且BC=2,以A为圆心,AC为半径画弧,交数轴于点D,则点D表示的数为( )
A.2.2 B. C. D.
2、在△ABC中,∠B=90°,若BC=3,AC=5,则AB等于( )
A.2??????? B.3?????? C.4???????? D.
3、如图,在正方形网格中,每个正方形的边长为1,则在△ABC中,边长为无理数的边数是( )
A.0???? B.1?????? C.2???????? D.3
4、若直角三角形的三边长分别为2,4,x,则x的值可能有(??? ).
A.1个???? B.2个 C.3个????? D.4个
5、直角三角形的两直角边分别为5cm,12cm,其斜边上的高为( )
A.6cm? B.8.5cm??? C.cm?? D.cm
6、我国是最早了解勾股定理的国家之一.下面四幅图中,不能证明勾股定理的是( )
A. B. C. D.
7、“折竹抵地”问题源自《九章算术》中,即:今有竹高一丈,末折抵地,去本四尺,问折者高几何?意思是:一根竹子,原高一丈,一阵风将竹子折断,其竹梢恰好抵地,抵地处离竹子底部4尺远,则折断后的竹子高度为多少尺?(1丈=10尺)( )
A.3??????? B.5????? C.4.2??????? D.4
8、为迎接新年的到来,同学们做了许多拉花布置教室,准备召开新年晚会,小刘搬来一架高2.5米的木梯,准备把拉花挂到2.4米高的墙上,则梯脚与墙角距离应为( )
A.0.7米?? ? B.0.8米?? ? C.0.9米??? D.1.0米
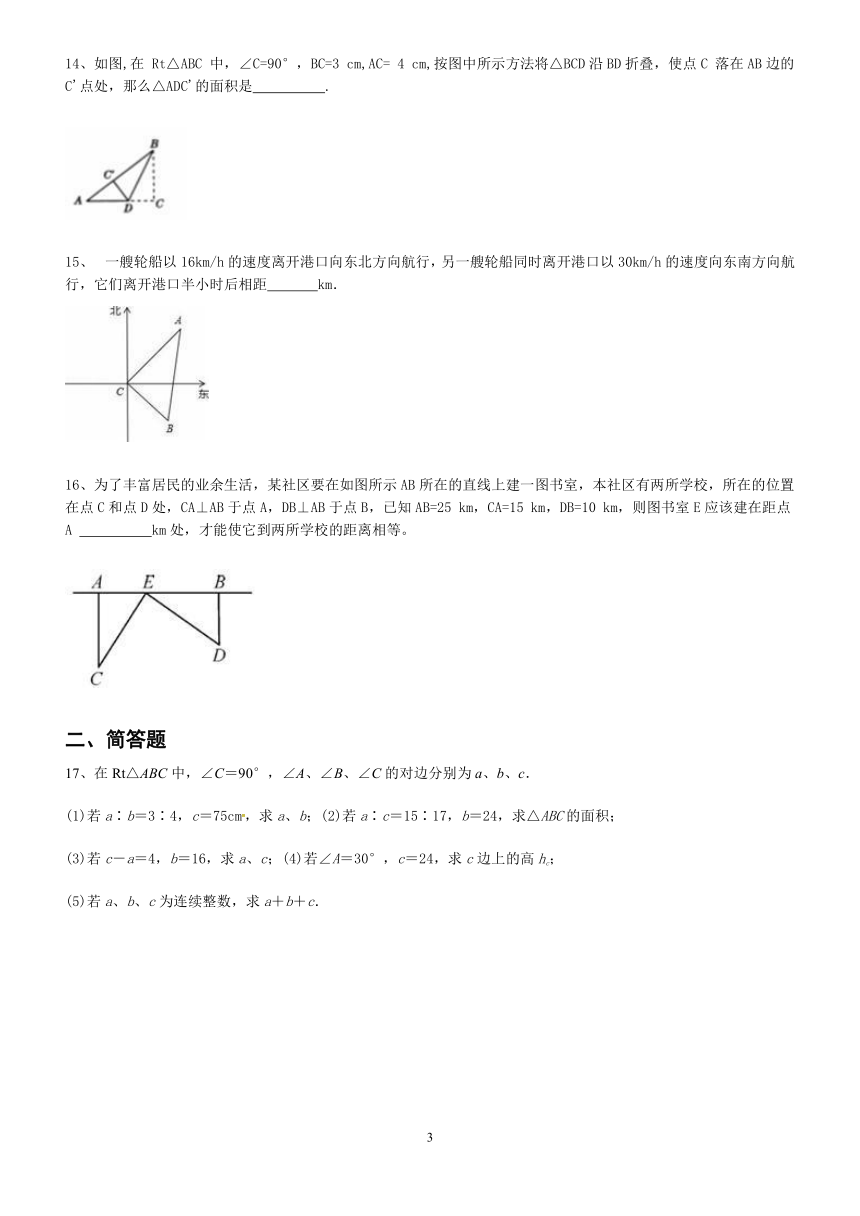
9、如图,小明在广场上先向东走10米,又向南走40米,再向西走20米,又向南走40米,再向东走70米.则小明到达的终止点与原出发点的距离是( )
A.90米? ??? B.100米???? C.120米??? ??? ??? D.150米
?? ???????????
10、我国古代数学家刘徽将勾股形(古人称直角三角形为勾股形)分割成一个正方形和两对全等的三角形,如图所示,已知∠A=90°,BD=4,CF=6,则正方形ADOF的边长是( )
A.??????? B.2???????? C.??????? D.4
二、填空题
11、有两根木棒,分别长6cm、5cm,要再在7cm的木棒上取一段,用这三根木棒为边做成直角三角形,这第三根木棒要取的长度是 ?? .
12、.如图,写出字母所代表的正方形面积,SA= ?? ,SB= ?? .
13、如图,长方形网格中每个小正方形的边长是1,△ABC是格点三角形(顶点都在格点上),则点C到AB的距离为 ?? .
14、如图,在 Rt△ABC 中,∠C=90°,BC=3 cm,AC= 4 cm,按图中所示方法将△BCD沿BD折叠,使点C 落在AB边的C'点处,那么△ADC'的面积是?????.
15、?一艘轮船以16km/h的速度离开港口向东北方向航行,另一艘轮船同时离开港口以30km/h的速度向东南方向航行,它们离开港口半小时后相距??? km.?
16、为了丰富居民的业余生活,某社区要在如图所示AB所在的直线上建一图书室,本社区有两所学校,所在的位置在点C和点D处,CA⊥AB于点A,DB⊥AB于点B,已知AB=25 km,CA=15 km,DB=10 km,则图书室E应该建在距点A ?????km处,才能使它到两所学校的距离相等。
简答题
17、在Rt△ABC中,∠C=90°,∠A、∠B、∠C的对边分别为a、b、c.
(1)若a∶b=3∶4,c=75cm,求a、b;(2)若a∶c=15∶17,b=24,求△ABC的面积;
(3)若c-a=4,b=16,求a、c;(4)若∠A=30°,c=24,求c边上的高hc;
(5)若a、b、c为连续整数,求a+b+c.
18、如图,梯子AB斜靠在一竖直的墙上,梯子的底端A到墙根O的距离AO为2米,梯子的顶端B到地面的距离BO为6米,现将梯子的底端A向外移动到A′,使梯子的底端A′到墙根O的距离A′O等于3米,同时梯子的顶端B下降至B′.求梯子顶端下滑的距离BB′.
19、?小明想知道学校旗杆的高,他发现旗杆上的绳子垂到地面还多了1m,当他把绳子的下端拉开5m后,发现下端刚好接触地面,求旗杆的高.
20、如图,某人欲横渡一条河,由于水流的影响,实际上岸地点C偏离欲到达点B200m,结果他在水中实际游了520m,该河流的宽度为多少?
21、如图,在一棵树的10米高B处有两只猴子,其中一只爬下树走向离树20米的池塘C,而另一只爬到树顶D后直扑池塘C,结果两只猴子经过的距离相等,问这棵树有多高?
参考答案
一、选择题
1、D;2、C;3、D;4、B.;5、D;6、D;7、C;8、A;9、B;10、B;
二、填空题
11: cm.
12、625??? 144
13、1.2.
14、
15、 17.
16、10.
三、简答题
17、(1)a=45cm.b=60cm;?? (2)540;?? (3)a=30,c=34;
(4)6;?? (5)12.
18、解:在△RtAOB中,由勾股定理可知AB2=AO2+OB2=40,在Rt△A′OB′中由勾股定理可知A′B′2=A′O2+OB′2.
∵AB=A′B′,
∴A′O2+OB′2=40.
∴OB′==.
∴BB′=6﹣.
19、?解:设旗杆的高AB为xm,则绳子AC的长为(x+1)m
在Rt△ABC中,AB2+BC2=AC2
∴x2+52=(x+1)2
解得x=12
∴AB=12
∴旗杆的高12m.
20、?解:根据图中数据,运用勾股定理求得AB===480m,
答:该河流的宽度为480m.
21、分析:首先根据题意,正确画出图形,还要根据题意确定已知线段的长,再根据勾股定理列方程进行计算.
解:设BD=x米,则AD=(10+x)米,CD=(30-x)米,
根据题意,得:
(30-x)2-(x+10)2=202,
解得x=5.
即树的高度是10+5=15米.
选择题
1、如图,数轴上点A对应的数是0,点B对应的数是1,BC⊥AB,垂足为B,且BC=2,以A为圆心,AC为半径画弧,交数轴于点D,则点D表示的数为( )
A.2.2 B. C. D.
2、在△ABC中,∠B=90°,若BC=3,AC=5,则AB等于( )
A.2??????? B.3?????? C.4???????? D.
3、如图,在正方形网格中,每个正方形的边长为1,则在△ABC中,边长为无理数的边数是( )
A.0???? B.1?????? C.2???????? D.3
4、若直角三角形的三边长分别为2,4,x,则x的值可能有(??? ).
A.1个???? B.2个 C.3个????? D.4个
5、直角三角形的两直角边分别为5cm,12cm,其斜边上的高为( )
A.6cm? B.8.5cm??? C.cm?? D.cm
6、我国是最早了解勾股定理的国家之一.下面四幅图中,不能证明勾股定理的是( )
A. B. C. D.
7、“折竹抵地”问题源自《九章算术》中,即:今有竹高一丈,末折抵地,去本四尺,问折者高几何?意思是:一根竹子,原高一丈,一阵风将竹子折断,其竹梢恰好抵地,抵地处离竹子底部4尺远,则折断后的竹子高度为多少尺?(1丈=10尺)( )
A.3??????? B.5????? C.4.2??????? D.4
8、为迎接新年的到来,同学们做了许多拉花布置教室,准备召开新年晚会,小刘搬来一架高2.5米的木梯,准备把拉花挂到2.4米高的墙上,则梯脚与墙角距离应为( )
A.0.7米?? ? B.0.8米?? ? C.0.9米??? D.1.0米
9、如图,小明在广场上先向东走10米,又向南走40米,再向西走20米,又向南走40米,再向东走70米.则小明到达的终止点与原出发点的距离是( )
A.90米? ??? B.100米???? C.120米??? ??? ??? D.150米
?? ???????????
10、我国古代数学家刘徽将勾股形(古人称直角三角形为勾股形)分割成一个正方形和两对全等的三角形,如图所示,已知∠A=90°,BD=4,CF=6,则正方形ADOF的边长是( )
A.??????? B.2???????? C.??????? D.4
二、填空题
11、有两根木棒,分别长6cm、5cm,要再在7cm的木棒上取一段,用这三根木棒为边做成直角三角形,这第三根木棒要取的长度是 ?? .
12、.如图,写出字母所代表的正方形面积,SA= ?? ,SB= ?? .
13、如图,长方形网格中每个小正方形的边长是1,△ABC是格点三角形(顶点都在格点上),则点C到AB的距离为 ?? .
14、如图,在 Rt△ABC 中,∠C=90°,BC=3 cm,AC= 4 cm,按图中所示方法将△BCD沿BD折叠,使点C 落在AB边的C'点处,那么△ADC'的面积是?????.
15、?一艘轮船以16km/h的速度离开港口向东北方向航行,另一艘轮船同时离开港口以30km/h的速度向东南方向航行,它们离开港口半小时后相距??? km.?
16、为了丰富居民的业余生活,某社区要在如图所示AB所在的直线上建一图书室,本社区有两所学校,所在的位置在点C和点D处,CA⊥AB于点A,DB⊥AB于点B,已知AB=25 km,CA=15 km,DB=10 km,则图书室E应该建在距点A ?????km处,才能使它到两所学校的距离相等。
简答题
17、在Rt△ABC中,∠C=90°,∠A、∠B、∠C的对边分别为a、b、c.
(1)若a∶b=3∶4,c=75cm,求a、b;(2)若a∶c=15∶17,b=24,求△ABC的面积;
(3)若c-a=4,b=16,求a、c;(4)若∠A=30°,c=24,求c边上的高hc;
(5)若a、b、c为连续整数,求a+b+c.
18、如图,梯子AB斜靠在一竖直的墙上,梯子的底端A到墙根O的距离AO为2米,梯子的顶端B到地面的距离BO为6米,现将梯子的底端A向外移动到A′,使梯子的底端A′到墙根O的距离A′O等于3米,同时梯子的顶端B下降至B′.求梯子顶端下滑的距离BB′.
19、?小明想知道学校旗杆的高,他发现旗杆上的绳子垂到地面还多了1m,当他把绳子的下端拉开5m后,发现下端刚好接触地面,求旗杆的高.
20、如图,某人欲横渡一条河,由于水流的影响,实际上岸地点C偏离欲到达点B200m,结果他在水中实际游了520m,该河流的宽度为多少?
21、如图,在一棵树的10米高B处有两只猴子,其中一只爬下树走向离树20米的池塘C,而另一只爬到树顶D后直扑池塘C,结果两只猴子经过的距离相等,问这棵树有多高?
参考答案
一、选择题
1、D;2、C;3、D;4、B.;5、D;6、D;7、C;8、A;9、B;10、B;
二、填空题
11: cm.
12、625??? 144
13、1.2.
14、
15、 17.
16、10.
三、简答题
17、(1)a=45cm.b=60cm;?? (2)540;?? (3)a=30,c=34;
(4)6;?? (5)12.
18、解:在△RtAOB中,由勾股定理可知AB2=AO2+OB2=40,在Rt△A′OB′中由勾股定理可知A′B′2=A′O2+OB′2.
∵AB=A′B′,
∴A′O2+OB′2=40.
∴OB′==.
∴BB′=6﹣.
19、?解:设旗杆的高AB为xm,则绳子AC的长为(x+1)m
在Rt△ABC中,AB2+BC2=AC2
∴x2+52=(x+1)2
解得x=12
∴AB=12
∴旗杆的高12m.
20、?解:根据图中数据,运用勾股定理求得AB===480m,
答:该河流的宽度为480m.
21、分析:首先根据题意,正确画出图形,还要根据题意确定已知线段的长,再根据勾股定理列方程进行计算.
解:设BD=x米,则AD=(10+x)米,CD=(30-x)米,
根据题意,得:
(30-x)2-(x+10)2=202,
解得x=5.
即树的高度是10+5=15米.
