人教版七年级数学下册5.2.2 平行线的判定同步测试(含答案)
文档属性
| 名称 | 人教版七年级数学下册5.2.2 平行线的判定同步测试(含答案) |

|
|
| 格式 | zip | ||
| 文件大小 | 280.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-02-12 00:00:00 | ||
图片预览

文档简介
5.2.2 平行线的判定
一、选择题
1.如图,点E在BC的延长线上,下列条件中,能判定AB∥CD的是( )
A.∠DBC=∠DAC B.∠ABC=∠DCE
C.∠ADC=∠DCE D.∠ADC+∠BCD=180°
2.下列选项中,不能判定直线l1∥l2的是( )
A.∠1=∠3 B.∠4=∠5 C.∠1=∠2 D.∠2+∠4=180°
3.如图,已知∠2=110°,要使a∥b,则需具备的另一个条件为( )
A.∠3=70° B.∠3=110° C.∠4=70° D.∠1=70°
4.如图,在下列条件:①∠1=∠2;②∠BAD=∠BCD;③∠ABC=∠ADC且∠3=∠4;④∠BAD+∠ABC=180°,其中能判定AB∥CD的有( )
A.3个 B.2个 C.1个 D.0个
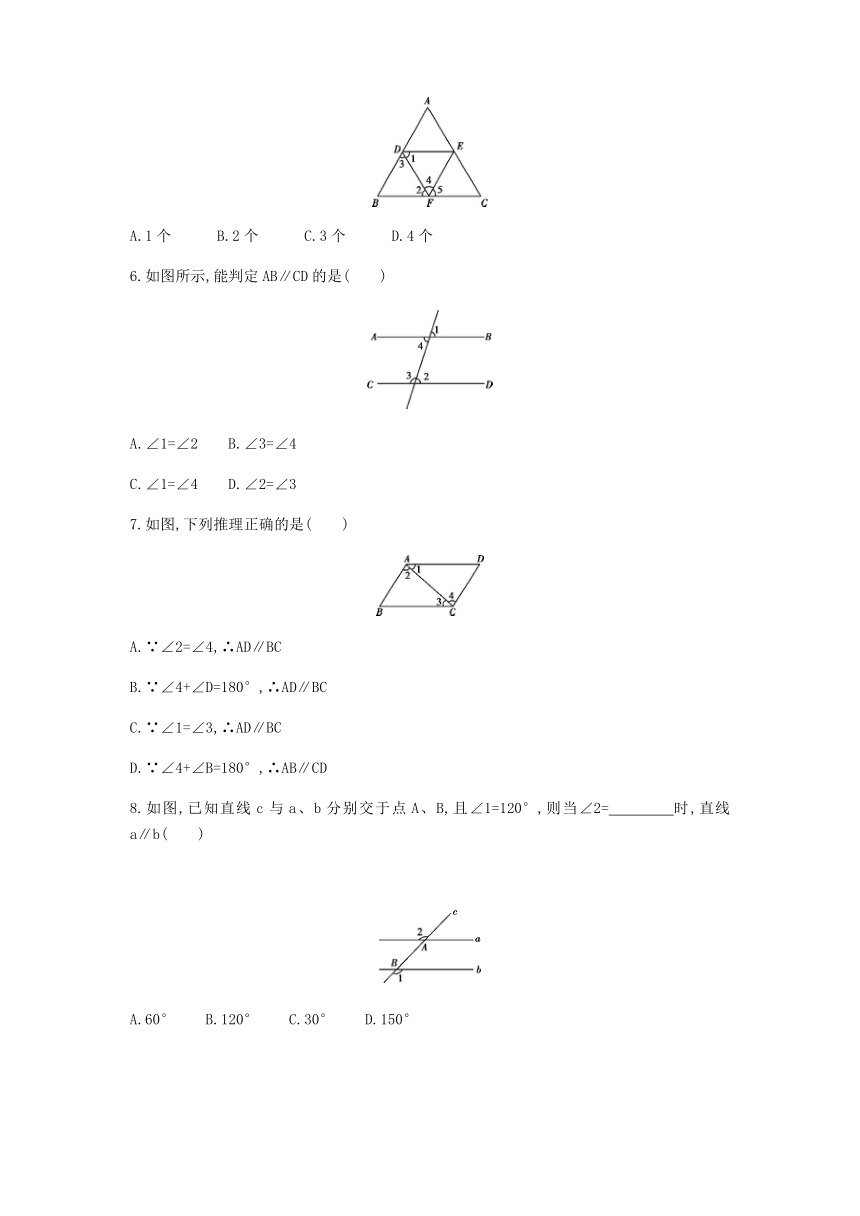
5.如图,下列条件中,能判定AB∥EF的有( )
①∠B+∠BFE=180°;②∠1=∠2;③∠3=∠4;④∠B=∠5.
A.1个 B.2个 C.3个 D.4个
6.如图所示,能判定AB∥CD的是( )
A.∠1=∠2 B.∠3=∠4
C.∠1=∠4 D.∠2=∠3
7.如图,下列推理正确的是( )
A.∵∠2=∠4,∴AD∥BC
B.∵∠4+∠D=180°,∴AD∥BC
C.∵∠1=∠3,∴AD∥BC
D.∵∠4+∠B=180°,∴AB∥CD
8.如图,已知直线c与a、b分别交于点A、B,且∠1=120°,则当∠2= 时,直线a∥b( )?
A.60° B.120° C.30° D.150°
二、填空题
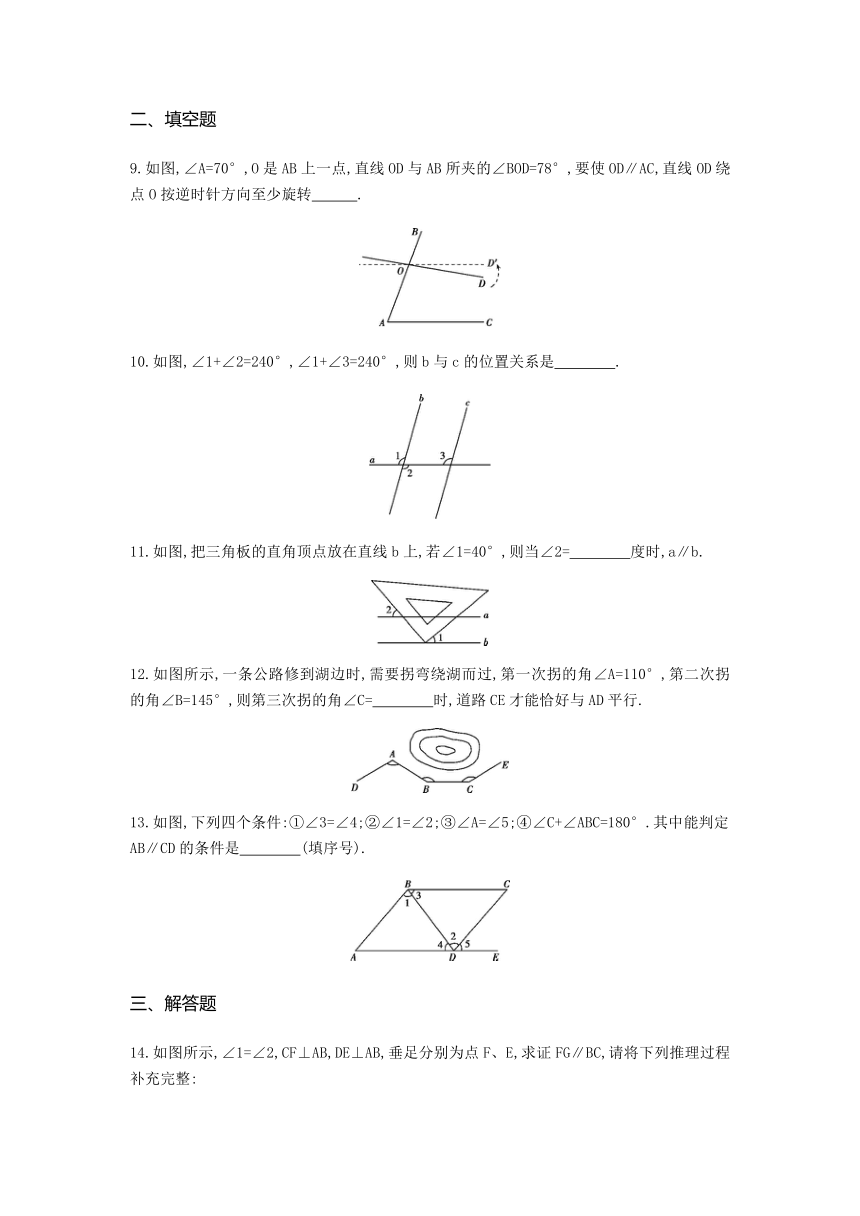
9.如图,∠A=70°,O是AB上一点,直线OD与AB所夹的∠BOD=78°,要使OD∥AC,直线OD绕点O按逆时针方向至少旋转 .?
10.如图,∠1+∠2=240°,∠1+∠3=240°,则b与c的位置关系是 .?
11.如图,把三角板的直角顶点放在直线b上,若∠1=40°,则当∠2= 度时,a∥b.?
12.如图所示,一条公路修到湖边时,需要拐弯绕湖而过,第一次拐的角∠A=110°,第二次拐的角∠B=145°,则第三次拐的角∠C= 时,道路CE才能恰好与AD平行.?
13.如图,下列四个条件:①∠3=∠4;②∠1=∠2;③∠A=∠5;④∠C+∠ABC=180°.其中能判定AB∥CD的条件是 (填序号).?
三、解答题
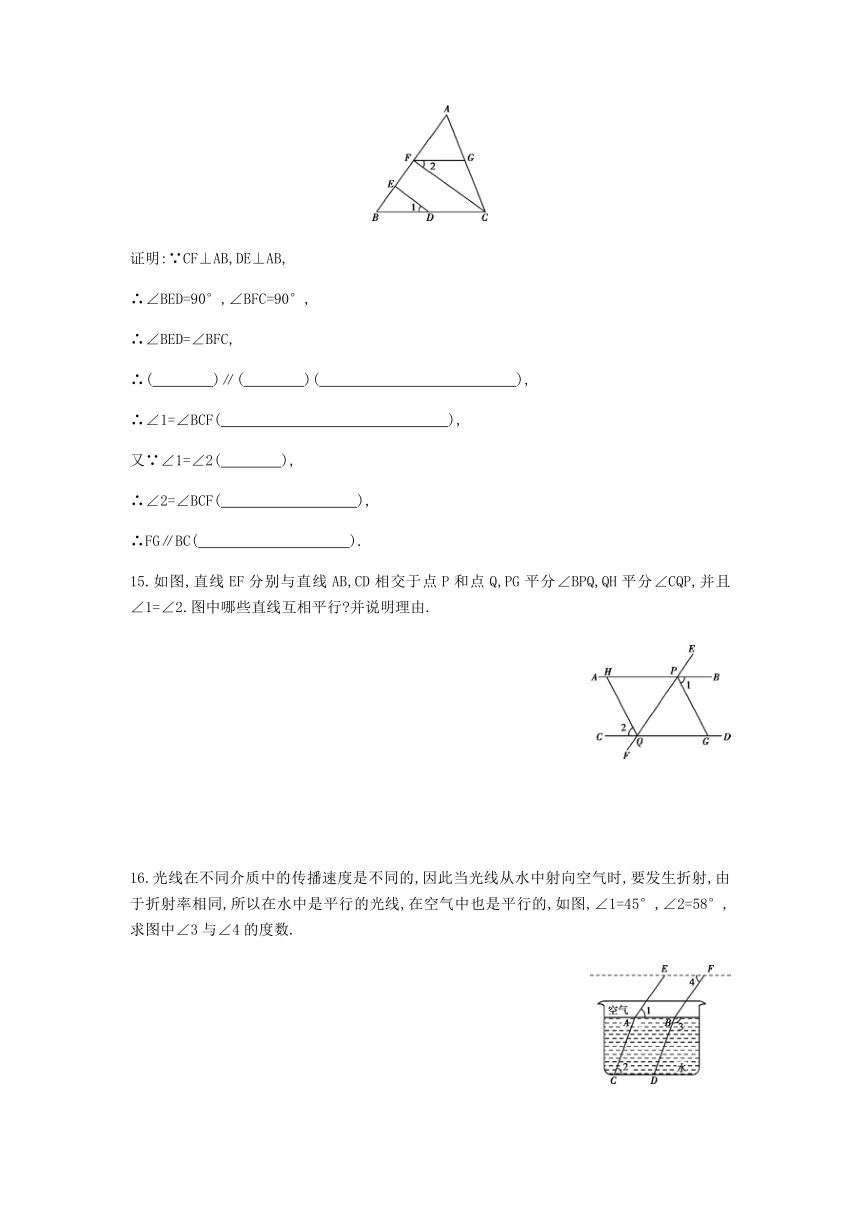
14.如图所示,∠1=∠2,CF⊥AB,DE⊥AB,垂足分别为点F、E,求证FG∥BC,请将下列推理过程补充完整:
证明:∵CF⊥AB,DE⊥AB,
∴∠BED=90°,∠BFC=90°,
∴∠BED=∠BFC,
∴( )∥( )( ),?
∴∠1=∠BCF( ),?
又∵∠1=∠2( ),?
∴∠2=∠BCF( ),?
∴FG∥BC( ).?
15.如图,直线EF分别与直线AB,CD相交于点P和点Q,PG平分∠BPQ,QH平分∠CQP,并且∠1=∠2.图中哪些直线互相平行?并说明理由.
16.光线在不同介质中的传播速度是不同的,因此当光线从水中射向空气时,要发生折射,由于折射率相同,所以在水中是平行的光线,在空气中也是平行的,如图,∠1=45°,∠2=58°,求图中∠3与∠4的度数.
17.如图,MF⊥NF于F,MF交AB于点E,NF交CD于点G,∠1=140°,∠2=50°,试判断AB和CD的位置关系,并说明理由.
18.如图,DA平分∠BDC,∠1=∠2,∠B+∠F=180°.
(1)写出3个∠B的同旁内角;
(2)若∠B=105°,求∠ADC的度数;
(3)求证:CD∥EF.
答案
1. B
2. C
3. A
4. C
5. C
6. A
7. C
8. B
9. 8°
10. b∥c
11. 50
12. 145°
13. ②③④
14.∵CF⊥AB,DE⊥AB,
∴∠BED=90°,∠BFG=90°,
∴∠BED=∠BFC,
∴ED∥FC(同位角相等,两直线平行),
∴∠1=∠BCF(两直线平行,同位角相等),
又∵∠1=∠2(已知),
∴∠2=∠BCF(等量代换),
∴FG∥BC(内错角相等,两直线平行).
15.AB∥CD,QH∥PG.
理由:∵PG平分∠BPQ,QH平分∠CQP,
∴∠GPQ=∠1=∠BPQ,∠HQP=∠2=∠CQP,
∵∠1=∠2,
∴∠GPQ=∠HQP,∠BPQ=∠CQP,
∴QH∥PG,AB∥CD.
16.如图,∵AB∥CD,∠2=58°,
∴∠5=180°-58°=122°,
∵AC∥BD,
∴∠3=∠5=122°,
∵AE∥BF,
∴∠6=∠1=45°,
∵EF∥AB,
∴∠4=∠6=45°.
17.AB∥CD.理由如下:
如图,延长MF交CD于点H,
∵∠1=140°,∴∠FGH=180°-∠1=40°,∵MF⊥NF,∴∠GFH=90°,
∴∠CHF=180°-∠FGD-∠GFH=180°-40°-90°=50°,
又∵∠2=50°,∴∠CHF=∠2,
∴AB∥CD.
18.(1)∠B的同旁内角有∠1,∠BAC,∠2、∠BDC、∠F(任选3个即可).
(2)∵DA平分∠BDC,
∴∠ADC=∠2=∠BDC,
∵∠1=∠2,
∴∠1=∠ADC,
∴AB∥CD,
∴∠BDC=180°-∠B=180°-105°=75°,
∴∠ADC=∠BDC=×75°=37.5°.
(3)证明:由(2)得AB∥CD,
∵∠B+∠F=180°,
∴AB∥EF,
∴CD∥EF.
