人教版七年级数学下册 5.1 相交线同步练习
文档属性
| 名称 | 人教版七年级数学下册 5.1 相交线同步练习 | 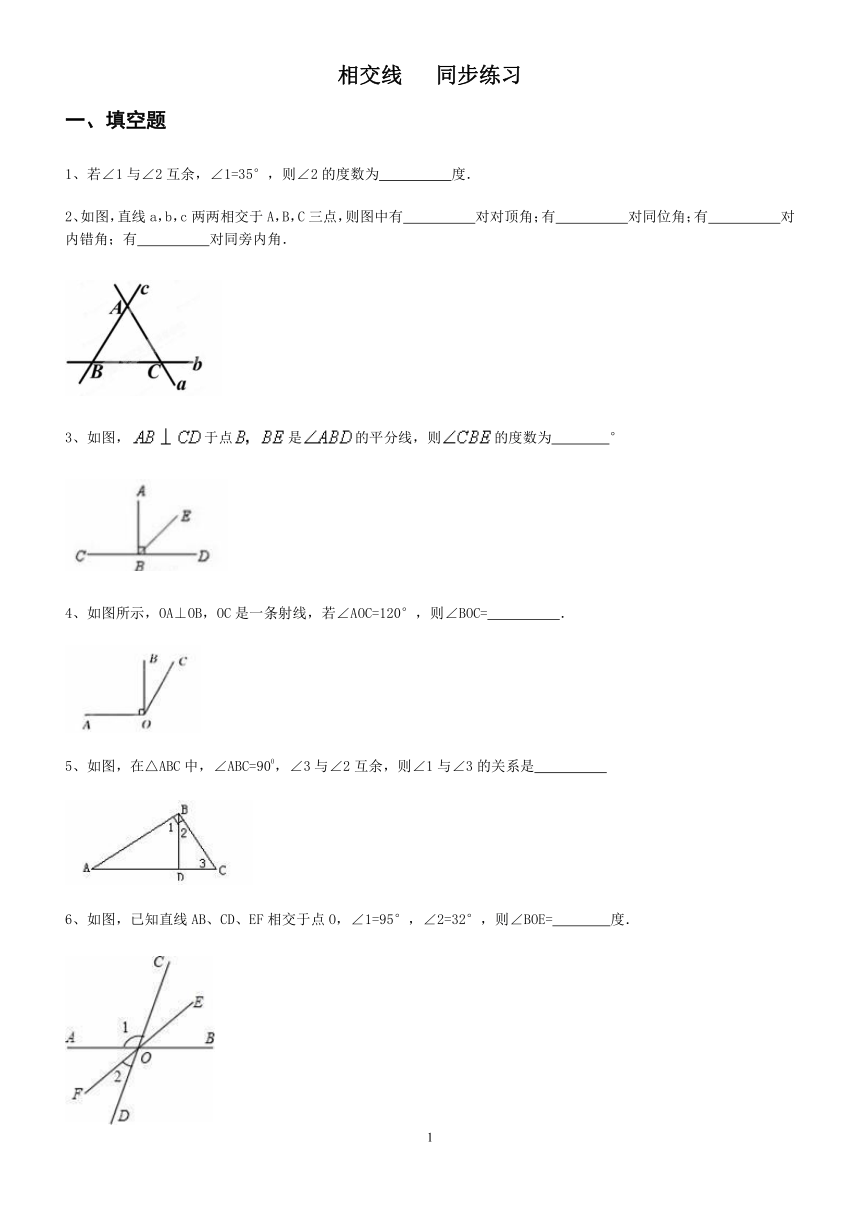 | |
| 格式 | zip | ||
| 文件大小 | 84.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-02-12 13:53:17 | ||
图片预览




文档简介
相交线 同步练习
一、填空题
1、若∠1与∠2互余,∠1=35°,则∠2的度数为 度.
2、如图,直线a,b,c两两相交于A,B,C三点,则图中有 对对顶角;有 对同位角;有 对内错角;有 对同旁内角.
3、如图,于点是的平分线,则的度数为????°
4、如图所示,OA⊥OB,OC是一条射线,若∠AOC=120°,则∠BOC= .
如图,在△ABC中,∠ABC=900,∠3与∠2互余,则∠1与∠3的关系是
6、如图,已知直线AB、CD、EF相交于点O,∠1=95°,∠2=32°,则∠BOE= 度.
二、选择题
7、已知:如图7所示,直线AB、CD被直线EF所截,则∠EMB的同位角是(?? )
A、∠AMF???? B、∠BMF??? C、∠ENC??? D、∠END?
8、如图,直线AB、CD被直线EF所截,则∠3的同旁内角是(?? ).?
A.∠1??? ???B.∠2 ????C.∠4???? ???D.∠5
9、下列语句中,正确的是(??? )
A.相等的角一定是对顶角? ?B.互为补角的两个角不相等??
C.两边互为反向处长线的两个角是对顶角?? D.交于一点的三条直线形成3对对顶角
10、如图,在所标识的角中,同位角是(???? ).
A.和??? B.和? C.和??? ? D.和
11、如图,∠ADE和∠CED是??? (??? )
A.同位角? ????? B.内错角? ????? C.同旁内角? ?????? D.互为补角
12、如图,∠1与∠2是同位角的图形有( )
A.1个????? B.2个 C.3个?????? D.4个
13、给出下列说法:
(1)两条直线被第三条直线所截,同位角相等;
(2)平面内的一条直线和两条平行线中的一条相交,则它与另一条也相交;
(3)相等的两个角是对顶角;
(4)从直线外一点到这条直线的垂线段,叫做这点到直线的距离;
其中正确的有(??? )
A? 0个?????? B? 1个?????? C? 2个?????? D? 3个
14、∠1与∠2是内错角,∠1=30°,则∠2的度数为?? (? ??)
A.30°?? ?? B.150°?????? C.30°或150°? ???? D.不能确定
15、如图,直线相交于点O,OM⊥,若,则β=(?? )
A.56°??? ? B.46°? ??? C.45°?? ???? D.44°
16、如图,已知直线AB、CD相交于点O,OE平分∠COB,若∠EOB=55o,则∠BOD的度数是(??? )
A.35o????????????? B.55o????????? C.70o????????? D.110o
?
17、如图,∠1=20°,AO⊥CO,点B、O、D在同一直线上,则∠2的度数为(???? )。
?
A、70°??? B、20°???? C、110°????? D、160°
18、如图,OA⊥OB,OC平分∠BOD,∠AOD=4∠1,则∠BOD的度数为( ).
A.45°???? B.60°??????? C.75°???????D.90°
三、简答题
19、如图所示,火车站、码头分别位于A,B两点,直线和分别表示河流与铁路.
(1)从火车站到码头怎样走最近,画图并说明理由;
(2)从码头到铁路怎样走最近,画图并说明理由;
(3)从火车站到河流怎样走最近,画图并说明理由.
20、如图,直线AB、CD相交于点O,OE⊥OC,若∠1=50°,分别求∠2,∠3的度数
21、如图,直线AB、CD相交于点O,OE平分∠AOD,∠FOC=90°,∠1=40°,求∠2和∠3的度数.
22、如图,直线AB、CD交于O点,且∠BOC=80°,OE平分∠BOC,OF为OE 的反向延长线.
? (1)求∠2和∠3的度数.
? (2)OF平分∠AOD吗?为什么?
23、直线AB、CD相交于O,OE平分∠AOC,∠EOA:∠AOD=1:4,求∠EOB的度数.
24、如图,直线AB.CD相交于点O,OE平分∠BOC,∠COF=90°.
(1)若∠BOE=70°,求∠AOF的度数;
(2)若∠BOD:∠BOE=1:2,求∠AOF的度数.
参考答案
一、填空题
1、 55 度.
2、6;12;6;6
3、135
4、30°??
5、∠1=∠3??
6、53 .
二、选择题
7、D;8、B;9、C;10、C;11、B;12、C;13、B;14、D;15、B;16、C;17、C;;18、D
三、简答题
19、(1)从火车站到码头走线段AB最近,理由:两点之间线段最短;
??? (2)从码头到铁路走BM最近,理由:垂线段最短;
??? (3)从火车站到河流走AN最近,理由垂线段最短.[来源:学_科_网Z_X_X_K][来源:Zxxk.Com]
20、解:∵OE⊥OC,
∴∠COE=90°,
∴∠1+∠2=180°﹣∠COE=90°,
∵∠1=50°,
∴∠2=40°,
∴∠3=180°﹣∠2=140°,
∴∠3+∠1=140°+50°=190°
21、解:因为 ∠FOC=90°,∠1=40°,AB为直线,
所以 ∠3+∠FOC+∠1=180°,所以 ∠3=180°-90°-40°=50°.
因为 ∠3与∠AOD互补,所以 ∠AOD =180°-∠3=130°.
因为 OE平分∠AOD,所以 ∠2=∠AOD=65°.
22、?(1)∠2=100°,∠3=40°;(2)∠AOF=40°,OF平分∠AOD?
23、解:∵OE平分∠AOC,
∴∠AOC=2x,
∵∠EOA:∠AOD=1:4,
∴∠AOD=4x,
∵∠COA+∠AOD=180°,
∴2x+4x=180°,
解得x=30°,
∴∠EOB=180°﹣30=150°.
故∠EOB的度数是150°.
24、解:(1)∵OE平分∠BOC,∠BOE=70°,
∴∠BOC=2∠BOE=140°,
∴∠AOC=180°﹣140°=40°,又∠COF=90°,
∴∠AOF=90°﹣40°=50°;
(2)∵∠BOD:∠BOE=1:2,OE平分∠BOC,
∴∠BOD:∠BOE:∠EOC=1:2:2,
∴∠BOD=36°,
∴∠AOC=36°,
又∵∠COF=90°,
∴∠AOF=90°﹣36°=54°.
一、填空题
1、若∠1与∠2互余,∠1=35°,则∠2的度数为 度.
2、如图,直线a,b,c两两相交于A,B,C三点,则图中有 对对顶角;有 对同位角;有 对内错角;有 对同旁内角.
3、如图,于点是的平分线,则的度数为????°
4、如图所示,OA⊥OB,OC是一条射线,若∠AOC=120°,则∠BOC= .
如图,在△ABC中,∠ABC=900,∠3与∠2互余,则∠1与∠3的关系是
6、如图,已知直线AB、CD、EF相交于点O,∠1=95°,∠2=32°,则∠BOE= 度.
二、选择题
7、已知:如图7所示,直线AB、CD被直线EF所截,则∠EMB的同位角是(?? )
A、∠AMF???? B、∠BMF??? C、∠ENC??? D、∠END?
8、如图,直线AB、CD被直线EF所截,则∠3的同旁内角是(?? ).?
A.∠1??? ???B.∠2 ????C.∠4???? ???D.∠5
9、下列语句中,正确的是(??? )
A.相等的角一定是对顶角? ?B.互为补角的两个角不相等??
C.两边互为反向处长线的两个角是对顶角?? D.交于一点的三条直线形成3对对顶角
10、如图,在所标识的角中,同位角是(???? ).
A.和??? B.和? C.和??? ? D.和
11、如图,∠ADE和∠CED是??? (??? )
A.同位角? ????? B.内错角? ????? C.同旁内角? ?????? D.互为补角
12、如图,∠1与∠2是同位角的图形有( )
A.1个????? B.2个 C.3个?????? D.4个
13、给出下列说法:
(1)两条直线被第三条直线所截,同位角相等;
(2)平面内的一条直线和两条平行线中的一条相交,则它与另一条也相交;
(3)相等的两个角是对顶角;
(4)从直线外一点到这条直线的垂线段,叫做这点到直线的距离;
其中正确的有(??? )
A? 0个?????? B? 1个?????? C? 2个?????? D? 3个
14、∠1与∠2是内错角,∠1=30°,则∠2的度数为?? (? ??)
A.30°?? ?? B.150°?????? C.30°或150°? ???? D.不能确定
15、如图,直线相交于点O,OM⊥,若,则β=(?? )
A.56°??? ? B.46°? ??? C.45°?? ???? D.44°
16、如图,已知直线AB、CD相交于点O,OE平分∠COB,若∠EOB=55o,则∠BOD的度数是(??? )
A.35o????????????? B.55o????????? C.70o????????? D.110o
?
17、如图,∠1=20°,AO⊥CO,点B、O、D在同一直线上,则∠2的度数为(???? )。
?
A、70°??? B、20°???? C、110°????? D、160°
18、如图,OA⊥OB,OC平分∠BOD,∠AOD=4∠1,则∠BOD的度数为( ).
A.45°???? B.60°??????? C.75°???????D.90°
三、简答题
19、如图所示,火车站、码头分别位于A,B两点,直线和分别表示河流与铁路.
(1)从火车站到码头怎样走最近,画图并说明理由;
(2)从码头到铁路怎样走最近,画图并说明理由;
(3)从火车站到河流怎样走最近,画图并说明理由.
20、如图,直线AB、CD相交于点O,OE⊥OC,若∠1=50°,分别求∠2,∠3的度数
21、如图,直线AB、CD相交于点O,OE平分∠AOD,∠FOC=90°,∠1=40°,求∠2和∠3的度数.
22、如图,直线AB、CD交于O点,且∠BOC=80°,OE平分∠BOC,OF为OE 的反向延长线.
? (1)求∠2和∠3的度数.
? (2)OF平分∠AOD吗?为什么?
23、直线AB、CD相交于O,OE平分∠AOC,∠EOA:∠AOD=1:4,求∠EOB的度数.
24、如图,直线AB.CD相交于点O,OE平分∠BOC,∠COF=90°.
(1)若∠BOE=70°,求∠AOF的度数;
(2)若∠BOD:∠BOE=1:2,求∠AOF的度数.
参考答案
一、填空题
1、 55 度.
2、6;12;6;6
3、135
4、30°??
5、∠1=∠3??
6、53 .
二、选择题
7、D;8、B;9、C;10、C;11、B;12、C;13、B;14、D;15、B;16、C;17、C;;18、D
三、简答题
19、(1)从火车站到码头走线段AB最近,理由:两点之间线段最短;
??? (2)从码头到铁路走BM最近,理由:垂线段最短;
??? (3)从火车站到河流走AN最近,理由垂线段最短.[来源:学_科_网Z_X_X_K][来源:Zxxk.Com]
20、解:∵OE⊥OC,
∴∠COE=90°,
∴∠1+∠2=180°﹣∠COE=90°,
∵∠1=50°,
∴∠2=40°,
∴∠3=180°﹣∠2=140°,
∴∠3+∠1=140°+50°=190°
21、解:因为 ∠FOC=90°,∠1=40°,AB为直线,
所以 ∠3+∠FOC+∠1=180°,所以 ∠3=180°-90°-40°=50°.
因为 ∠3与∠AOD互补,所以 ∠AOD =180°-∠3=130°.
因为 OE平分∠AOD,所以 ∠2=∠AOD=65°.
22、?(1)∠2=100°,∠3=40°;(2)∠AOF=40°,OF平分∠AOD?
23、解:∵OE平分∠AOC,
∴∠AOC=2x,
∵∠EOA:∠AOD=1:4,
∴∠AOD=4x,
∵∠COA+∠AOD=180°,
∴2x+4x=180°,
解得x=30°,
∴∠EOB=180°﹣30=150°.
故∠EOB的度数是150°.
24、解:(1)∵OE平分∠BOC,∠BOE=70°,
∴∠BOC=2∠BOE=140°,
∴∠AOC=180°﹣140°=40°,又∠COF=90°,
∴∠AOF=90°﹣40°=50°;
(2)∵∠BOD:∠BOE=1:2,OE平分∠BOC,
∴∠BOD:∠BOE:∠EOC=1:2:2,
∴∠BOD=36°,
∴∠AOC=36°,
又∵∠COF=90°,
∴∠AOF=90°﹣36°=54°.
