人教版七年级数学 下册 7.1.1 有序实数对 课件(共31张PPT)
文档属性
| 名称 | 人教版七年级数学 下册 7.1.1 有序实数对 课件(共31张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 1.3MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-02-12 00:00:00 | ||
图片预览










文档简介
(共31张PPT)
名言欣赏:
数学是打开科学大门的钥匙。
——培根
实数
有理数
无理数
整数
分数
(无限不循环小数)
小数
(有限小数或无限循环小数)
1)含有∏的数
2)开不尽方的数
形0.3030030003…类的小数
知识回顾
每一个有理数都可以用数轴上的点表示;每一个无理数都可以用数轴上的点表示;
数轴上的点有些表示有理数,有些表示无理数。
每一个实数都可以用数轴上的一个点来表示;反过来,数轴上的每一点都表示一个实数。
即实数和数轴上的点是一一对应的。
在数轴上的两个点,右边的点表示的实数总比左边的点表示的实数大。
实数与数轴上点一一对应
知识回顾
扩大到面?
问题⑴: 新学期开始,老师要重新调整学生的座位,老师如何描述才能让学生准确地找到自己的新座位呢?
问题(2): 你认为确定一个位置需要几个数据?
提示一: 只给一个数据“第1列”。
提示二: 给出两个数据“第2排,第1列”。
排座
提出问题
7.1.1 有序实数对
人教版七年级数学 下册
目标导航
1.了解有序数对的概念;(重点)
2.结合实例进一步体会有序数对的意义,并会用有序数对表示物体的位置. (重点、难点)
自学提纲:(P64—65先独立阅读在小组交流)
1、什么是有序数对?书写有序数对时应注意什么问题?
2、举例说明有序数对有什么用途?
3、有序数对(a,b)和(b,a)一样吗?有什么区别?能举例说明吗?
4、你能举出在生活中用有序数对表示位置的例子吗?请举例说明。
自主研学
讲台
2
1
3
4
5
6
7
8
1
2
3
4
5
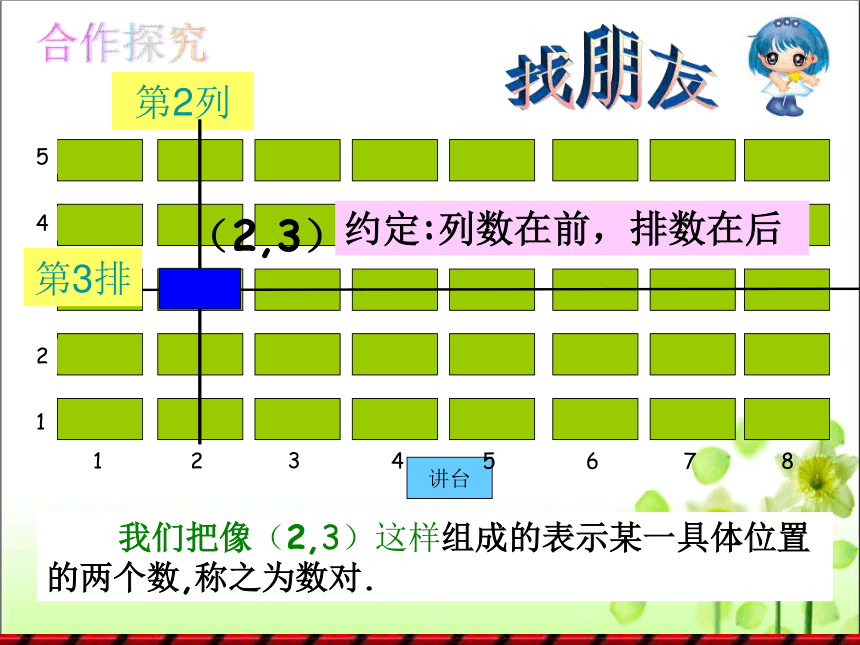
第2列
我们把像(2,3)这样组成的表示某一具体位置的两个数,称之为数对.
(2,3)
(列数,排数)
找朋友
约定:列数在前,排数在后
第3排
合作探究
数对
有顺序的两个数 a与 b 组成的数对叫做有序数对。
有序
记做:( a,b )
读做:数对a,b。
平面上物体的位置可以用有序数对来确定。
注意:(a,b)与(b,a)是不一样的
知识归纳
1. 这是某同学写出来的几个有序数对,哪些写对了?
A (5、9)
B (x,y)
E (6,9)
C 4,6
D (a b)
×
×
×
√
√
即学即练
利用有序数对,可以很准确地表示出一个位置.
知识引申
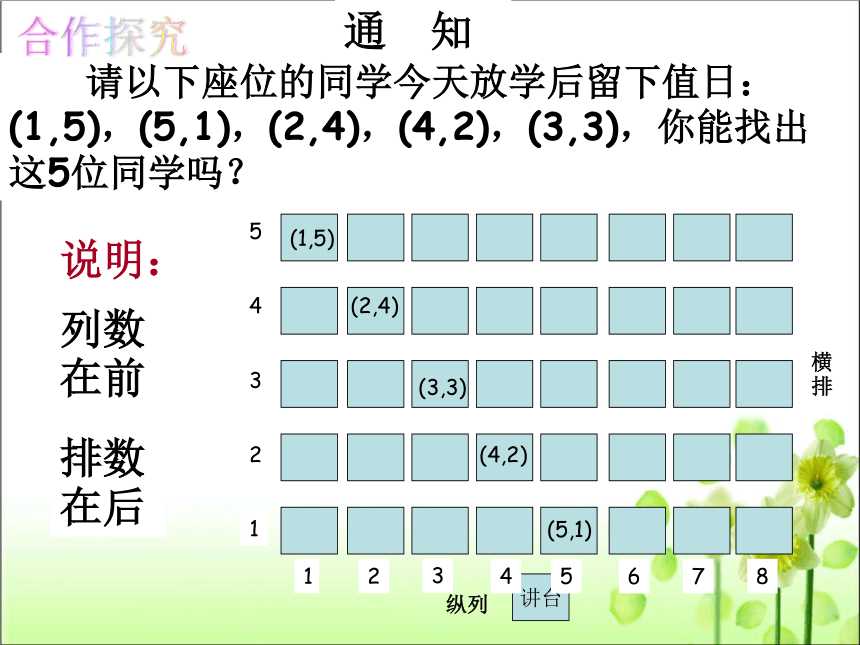
通 知
请以下座位的同学今天放学后留下值日:(1,5),(5,1),(2,4),(4,2),(3,3),你能找出这5位同学吗?
讲台
1
2
3
4
5
2
1
3
4
5
6
7
8
纵列
横排
(1,5)
列数在前
排数在后
(5,1)
(2,4)
(4,2)
(3,3)
说明:
合作探究
利用有序数对,可以很准确地表示出一个位置.
知识引申
扩大一点儿
下图是某校平面示意图,若大门所在位置为( 5,1 ), 则其余场所 所在的位置分别为( )
8
1
2
1
3
4
5
6
7
2
3
4
5
6
7
8
9
10
●
●
●
●
●
●
●
●
大门
食堂
宿舍楼
宣传橱窗
实验楼
教学楼
运动场
办公楼
(5,1)
(9,6)
(8,5)
(3,7)
(7,4)
(3,3)
(2,2)
(6,8)
合作探究
利用有序数对,可以很准确地表示出一个位置.
知识引申
再扩大一点儿
思考:在地球上如何确定城市的位置?
在地球上有横线和竖线,连接两极点的竖线叫经线,垂直于经线的横线圈为纬线.根据经纬线可以确定地球上任何一点的正确位置.
合作探究
北京:
东经116°
北纬40°
合作探究
例 如图,点A表示3街与5大道的十字路口,点B表示5街与3大道的十字路口,如果用(3,5)→(4,5) →(5,5)→(5,4)→(5,3)表示由A到B的一条路径,那么你能用同样的方法写出由A到B的其他几条路径吗?
6大道
1街 2街 3街 4街 5街 6街
?
?
B
A
1大道
2大道
3大道
4大道
5大道
典型例题
例 如图,点A表示3街与5大道的十字路口,点B表示5街与3大道的十字路口,如果用(3,5)→(4,5) →(5,5)→(5,4)→(5,3)表示由A到B的一条路径,那么你能用同样的方法写出由A到B的其他几条路径吗?
6大道
1街 2街 3街 4街 5街 6街
?
?
B
A
1大道
2大道
3大道
4大道
5大道
讨论:①图表表示什么意思?
②路径中每一对有序数对表达的含义是什么?
典型例题
例 如图,点A表示3街与5大道的十字路口,点B表示5街与3大道的十字路口,如果用(3,5)→(4,5) →(5,5)→(5,4)→(5,3)表示由A到B的一条路径,那么你能用同样的方法写出由A到B的其他几条路径吗?
6大道
1街 2街 3街 4街 5街 6街
?
?
B
A
1大道
2大道
3大道
4大道
5大道
如: (3,5)→(3,4) →(4,4)→(5,4)→(5,3)
典型例题
1.如图,甲处表示2街与5巷的十字路口,乙处表示5街与2巷的十字路口,如果用(2,5)表示甲处的位置,那么“(2,5)→(3,5) →(4,5) →(5,5) →(5,4) →(5,3) →(5,2)”表示从甲处到乙处的一种路线,请你用有序数对写出两种从甲处到乙处的不同的路线。
1巷
2巷
3巷
4巷
5巷
6巷
1街
2街
3街
4街
5街
6街
甲
乙
即学即练
8
1
2
3
4
5
6
7
1
2
3
4
5
6
7
8
9
10
●
●
●
●
●
●
●
●
大门
食堂
宿舍楼
宣传橱窗
实验楼
教学楼
运动场
办公楼
(9,6)
(8,5)
(3,7)
(6,8)
(7,4)
(2,2)
(3,3)
(5,2)
2.已知大门的位置,用有序数对表示学校里的各个地点.
即学即练
如果说“我家是(3,2),欢迎光临!”是不是同一位置呢?
欢乐时刻小游戏
规则:
老师点到谁的名字,表示老师想去他家作客,为了表示欢迎,这位同学要马上站起来并大声说出代表他的座位的有序数对。我们约定“列数在前,排数在后”.如XXX:“我家是(2,3),欢迎光临!”
即学即练
有序数对
有顺序的两个数a与b组成的数对叫 做有序数对,记作(a,b)。
(a,b)与(b,a)表示 的是两个不同的位置。
有序数对
点的位置
思想方法:
知识点:
注意点:
相互转化
数形结合
课堂小结
1、根据下列条件,说出能确定位置的有哪几个?
(1)座位是2排4号
(2)确山二中在东经114023ˊ37〞北纬32010ˊ7〞
(3)甲地距我市29km
√
√
检测目标
排
1
2
3
4
5
6
7
1
2
3
4
5
6
7
列
设计图案
2、如图( 1 , 3 )表示第一列第三排,请用彩笔把以下位置的五角星涂上颜色。
(4 ,6)
(3 ,4)
(5 ,4)
(2 ,2)
(4 ,2)
(6 ,2)
检测目标
1
2
3
4
5
6
7
8
9
10
2
3
4
5
6
8
9
7
1
(2,10)
(1,7)
(1,9)
(2,6)
(5,7)
●
●
●
●
●
●
(4,6)
3.我们知道:在象棋中,马行“日”字,如图,红“马”的位置用(3,8)表示,下一步红“马”可以走到的位置有几个?分别如何表示?
检测目标
我们已经站在了人生的起跑线上,为了实现心中的远大目标,我们正努力拼搏着。成功属于不畏困难、勇往直前的人。相信自己!
教师寄语
通过本课学习,你收获了什么?
课后作业:
完成教科书中相关练习题。
名言欣赏:
数学是打开科学大门的钥匙。
——培根
实数
有理数
无理数
整数
分数
(无限不循环小数)
小数
(有限小数或无限循环小数)
1)含有∏的数
2)开不尽方的数
形0.3030030003…类的小数
知识回顾
每一个有理数都可以用数轴上的点表示;每一个无理数都可以用数轴上的点表示;
数轴上的点有些表示有理数,有些表示无理数。
每一个实数都可以用数轴上的一个点来表示;反过来,数轴上的每一点都表示一个实数。
即实数和数轴上的点是一一对应的。
在数轴上的两个点,右边的点表示的实数总比左边的点表示的实数大。
实数与数轴上点一一对应
知识回顾
扩大到面?
问题⑴: 新学期开始,老师要重新调整学生的座位,老师如何描述才能让学生准确地找到自己的新座位呢?
问题(2): 你认为确定一个位置需要几个数据?
提示一: 只给一个数据“第1列”。
提示二: 给出两个数据“第2排,第1列”。
排座
提出问题
7.1.1 有序实数对
人教版七年级数学 下册
目标导航
1.了解有序数对的概念;(重点)
2.结合实例进一步体会有序数对的意义,并会用有序数对表示物体的位置. (重点、难点)
自学提纲:(P64—65先独立阅读在小组交流)
1、什么是有序数对?书写有序数对时应注意什么问题?
2、举例说明有序数对有什么用途?
3、有序数对(a,b)和(b,a)一样吗?有什么区别?能举例说明吗?
4、你能举出在生活中用有序数对表示位置的例子吗?请举例说明。
自主研学
讲台
2
1
3
4
5
6
7
8
1
2
3
4
5
第2列
我们把像(2,3)这样组成的表示某一具体位置的两个数,称之为数对.
(2,3)
(列数,排数)
找朋友
约定:列数在前,排数在后
第3排
合作探究
数对
有顺序的两个数 a与 b 组成的数对叫做有序数对。
有序
记做:( a,b )
读做:数对a,b。
平面上物体的位置可以用有序数对来确定。
注意:(a,b)与(b,a)是不一样的
知识归纳
1. 这是某同学写出来的几个有序数对,哪些写对了?
A (5、9)
B (x,y)
E (6,9)
C 4,6
D (a b)
×
×
×
√
√
即学即练
利用有序数对,可以很准确地表示出一个位置.
知识引申
通 知
请以下座位的同学今天放学后留下值日:(1,5),(5,1),(2,4),(4,2),(3,3),你能找出这5位同学吗?
讲台
1
2
3
4
5
2
1
3
4
5
6
7
8
纵列
横排
(1,5)
列数在前
排数在后
(5,1)
(2,4)
(4,2)
(3,3)
说明:
合作探究
利用有序数对,可以很准确地表示出一个位置.
知识引申
扩大一点儿
下图是某校平面示意图,若大门所在位置为( 5,1 ), 则其余场所 所在的位置分别为( )
8
1
2
1
3
4
5
6
7
2
3
4
5
6
7
8
9
10
●
●
●
●
●
●
●
●
大门
食堂
宿舍楼
宣传橱窗
实验楼
教学楼
运动场
办公楼
(5,1)
(9,6)
(8,5)
(3,7)
(7,4)
(3,3)
(2,2)
(6,8)
合作探究
利用有序数对,可以很准确地表示出一个位置.
知识引申
再扩大一点儿
思考:在地球上如何确定城市的位置?
在地球上有横线和竖线,连接两极点的竖线叫经线,垂直于经线的横线圈为纬线.根据经纬线可以确定地球上任何一点的正确位置.
合作探究
北京:
东经116°
北纬40°
合作探究
例 如图,点A表示3街与5大道的十字路口,点B表示5街与3大道的十字路口,如果用(3,5)→(4,5) →(5,5)→(5,4)→(5,3)表示由A到B的一条路径,那么你能用同样的方法写出由A到B的其他几条路径吗?
6大道
1街 2街 3街 4街 5街 6街
?
?
B
A
1大道
2大道
3大道
4大道
5大道
典型例题
例 如图,点A表示3街与5大道的十字路口,点B表示5街与3大道的十字路口,如果用(3,5)→(4,5) →(5,5)→(5,4)→(5,3)表示由A到B的一条路径,那么你能用同样的方法写出由A到B的其他几条路径吗?
6大道
1街 2街 3街 4街 5街 6街
?
?
B
A
1大道
2大道
3大道
4大道
5大道
讨论:①图表表示什么意思?
②路径中每一对有序数对表达的含义是什么?
典型例题
例 如图,点A表示3街与5大道的十字路口,点B表示5街与3大道的十字路口,如果用(3,5)→(4,5) →(5,5)→(5,4)→(5,3)表示由A到B的一条路径,那么你能用同样的方法写出由A到B的其他几条路径吗?
6大道
1街 2街 3街 4街 5街 6街
?
?
B
A
1大道
2大道
3大道
4大道
5大道
如: (3,5)→(3,4) →(4,4)→(5,4)→(5,3)
典型例题
1.如图,甲处表示2街与5巷的十字路口,乙处表示5街与2巷的十字路口,如果用(2,5)表示甲处的位置,那么“(2,5)→(3,5) →(4,5) →(5,5) →(5,4) →(5,3) →(5,2)”表示从甲处到乙处的一种路线,请你用有序数对写出两种从甲处到乙处的不同的路线。
1巷
2巷
3巷
4巷
5巷
6巷
1街
2街
3街
4街
5街
6街
甲
乙
即学即练
8
1
2
3
4
5
6
7
1
2
3
4
5
6
7
8
9
10
●
●
●
●
●
●
●
●
大门
食堂
宿舍楼
宣传橱窗
实验楼
教学楼
运动场
办公楼
(9,6)
(8,5)
(3,7)
(6,8)
(7,4)
(2,2)
(3,3)
(5,2)
2.已知大门的位置,用有序数对表示学校里的各个地点.
即学即练
如果说“我家是(3,2),欢迎光临!”是不是同一位置呢?
欢乐时刻小游戏
规则:
老师点到谁的名字,表示老师想去他家作客,为了表示欢迎,这位同学要马上站起来并大声说出代表他的座位的有序数对。我们约定“列数在前,排数在后”.如XXX:“我家是(2,3),欢迎光临!”
即学即练
有序数对
有顺序的两个数a与b组成的数对叫 做有序数对,记作(a,b)。
(a,b)与(b,a)表示 的是两个不同的位置。
有序数对
点的位置
思想方法:
知识点:
注意点:
相互转化
数形结合
课堂小结
1、根据下列条件,说出能确定位置的有哪几个?
(1)座位是2排4号
(2)确山二中在东经114023ˊ37〞北纬32010ˊ7〞
(3)甲地距我市29km
√
√
检测目标
排
1
2
3
4
5
6
7
1
2
3
4
5
6
7
列
设计图案
2、如图( 1 , 3 )表示第一列第三排,请用彩笔把以下位置的五角星涂上颜色。
(4 ,6)
(3 ,4)
(5 ,4)
(2 ,2)
(4 ,2)
(6 ,2)
检测目标
1
2
3
4
5
6
7
8
9
10
2
3
4
5
6
8
9
7
1
(2,10)
(1,7)
(1,9)
(2,6)
(5,7)
●
●
●
●
●
●
(4,6)
3.我们知道:在象棋中,马行“日”字,如图,红“马”的位置用(3,8)表示,下一步红“马”可以走到的位置有几个?分别如何表示?
检测目标
我们已经站在了人生的起跑线上,为了实现心中的远大目标,我们正努力拼搏着。成功属于不畏困难、勇往直前的人。相信自己!
教师寄语
通过本课学习,你收获了什么?
课后作业:
完成教科书中相关练习题。
