人教版七年级数学 下册 7.1.2 平面直角坐标系 课件(共33张PPT)
文档属性
| 名称 | 人教版七年级数学 下册 7.1.2 平面直角坐标系 课件(共33张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 738.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-02-12 00:00:00 | ||
图片预览







文档简介
(共33张PPT)
名言欣赏:
数学是打开科学大门的钥匙。
——培根
有序数对
有顺序的两个数a与b组成的数对叫 做有序数对,记作(a,b)。
(a,b)与(b,a)表示 的是两个不同的位置。
有序数对
点的位置
思想方法:
知识点:
注意点:
相互转化
数形结合
知识回顾
0
-5
-4
-3
-2
-1
1
2
3
4
5
6
-6
7
数轴上的点可以用一个数来表示,这个数叫做这个点在数轴上的坐标. 例如点A在数轴上的坐标为-3,点B在数轴上的坐标为2。反过来,知道数轴上一个点的坐标,这个的点在数轴上的位置也就确定了。
A
B
如何确定数轴上点的位置?
1米
知识回顾
雁塔
中心广场
钟楼
大成殿
科技大学
碑林
影月湖
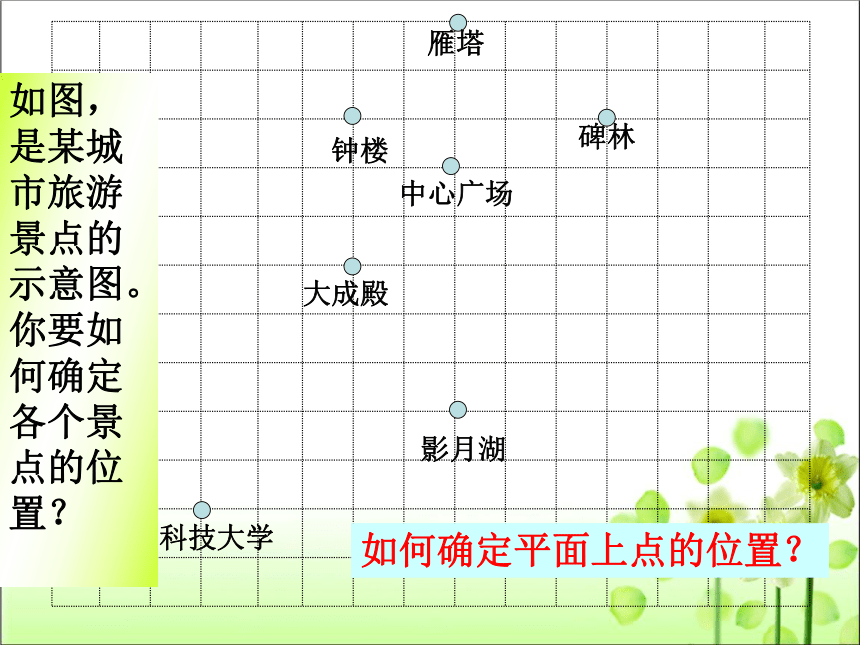
如图,是某城市旅游景点的示意图。你要如何确定各个景点的位置?
如何确定平面上点的位置?
7.1.2 平面直角坐标系
人教版七年级数学 下册
目标导航
1.知道平面直角坐标系的相关概念.
2.学会建立平面直角坐标系.
3.已知平面直角坐标系中的点,能说出它的坐标;已知点的坐标,能在平面直角坐标系中描出表示该坐标的点.
认真阅读课本中7.1.2 平面直角坐标系的内容,完成下面任务。
自主研学
学习任务:
1.如何确定一个点在数轴上的位置.
2.平面直角坐标系的概念,如何建立平面直角坐标系,象限划分.
根据点在数轴上的坐标可以直接确定该点在数轴上的位置.
1
2
3
-1
-2
-3
O
1
-1
2
-2
-3
3
x
y
x轴
横轴
y轴
纵轴
直角坐标
系的原点
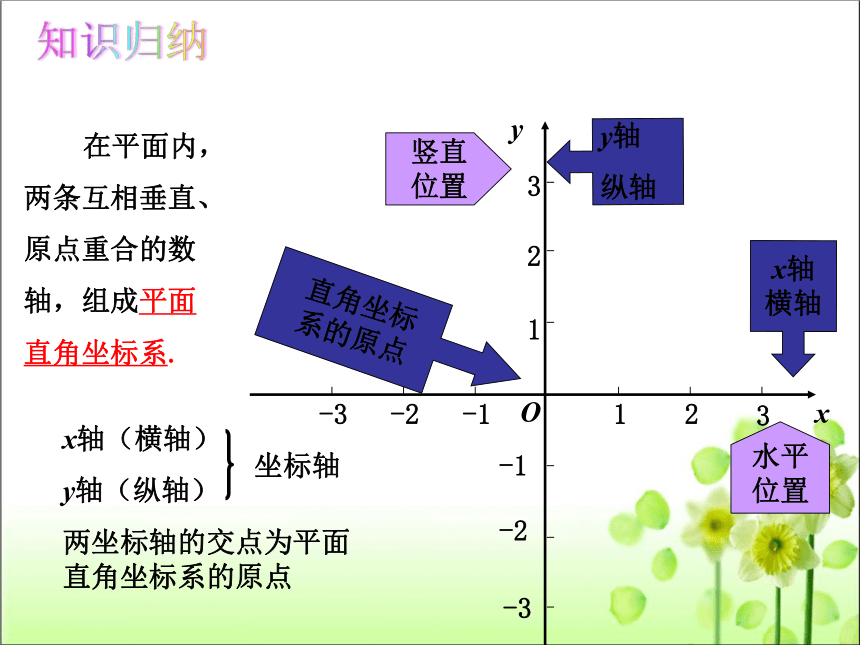
在平面内,两条互相垂直、原点重合的数轴,组成平面直角坐标系.
水平
位置
竖直
位置
x轴(横轴)
y轴(纵轴)
两坐标轴的交点为平面直角坐标系的原点
坐标轴
知识归纳
3
1
4
2
5
-2
-4
-1
-3
0
1
2
3
4
5
-4
-3
-2
-1
x
横轴
y
纵轴
原点
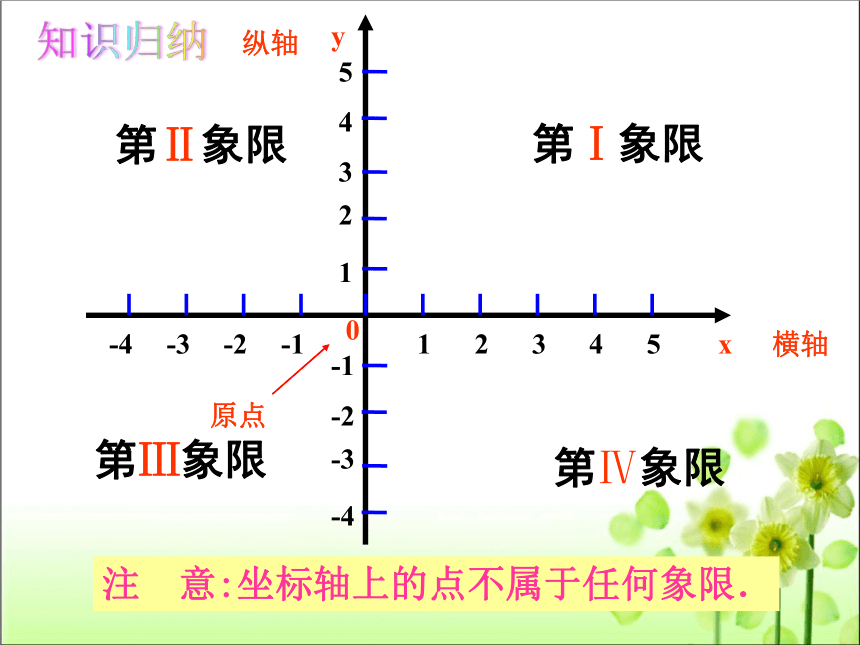
第Ⅰ象限
第Ⅳ象限
第Ⅲ象限
第Ⅱ象限
注 意:坐标轴上的点不属于任何象限.
知识归纳
·
A
3
1
4
2
5
-2
-4
-1
-3
0
1
2
3
4
5
-4
-3
-2
-1
x
横轴
y
纵轴
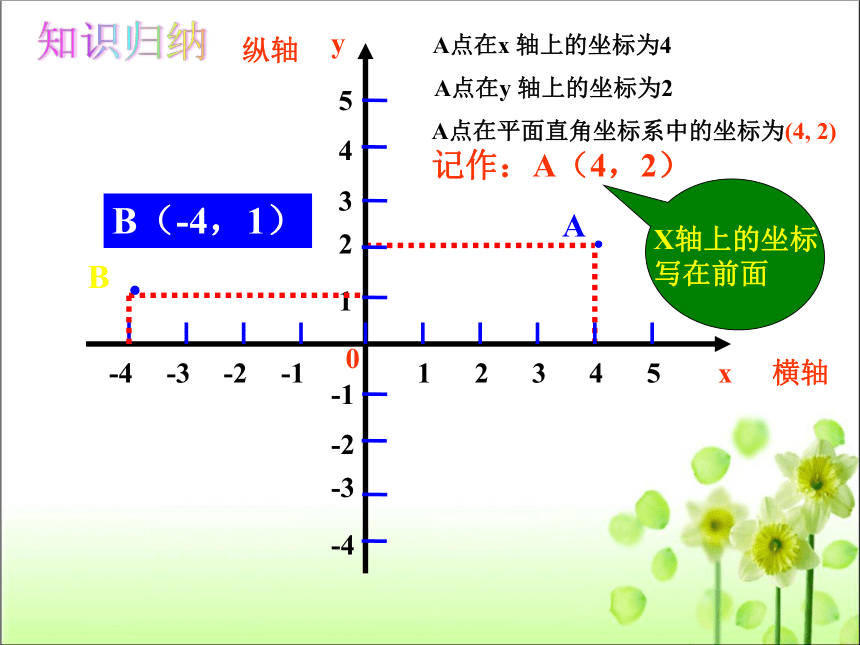
A点在x 轴上的坐标为4
A点在y 轴上的坐标为2
A点在平面直角坐标系中的坐标为(4, 2)
记作:A(4,2)
X轴上的坐标
写在前面
·
B
B(-4,1)
知识归纳
x
O
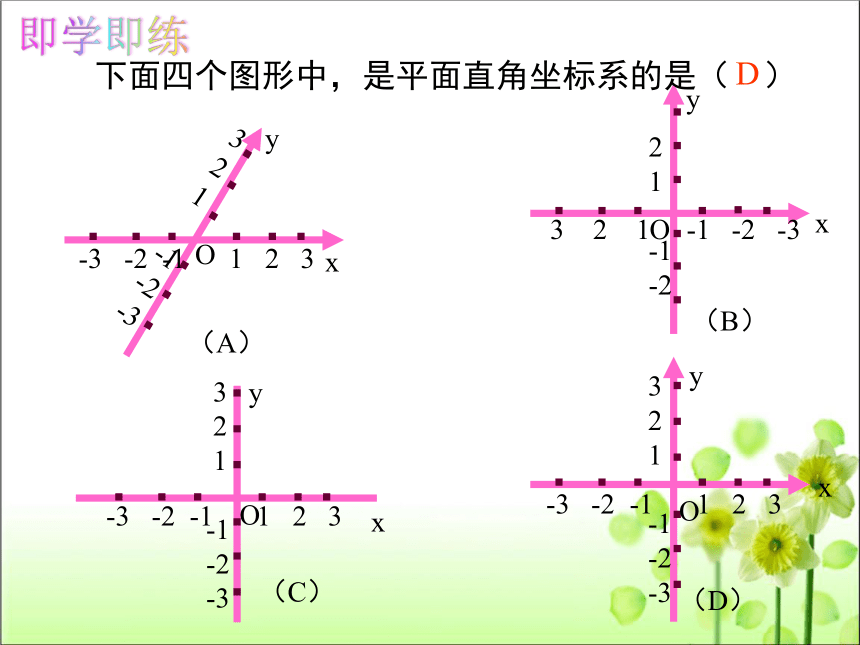
下面四个图形中,是平面直角坐标系的是( )
-3 -2 -1 1 2 3
3
2
1
-1
-2
-3
y
x
x
y
(A)
3 2 1 -1 -2 -3
x
y
(B)
2
1
-1
-2
O
-3 -2 -1 1 2 3
3
2
1
-1
-2
-3
(C)
O
-3 -2 -1 1 2 3
3
2
1
-1
-2
-3
y
(D)
O
D
即学即练
1.由点找坐标:
如何表示点A的位置?
1
1
-1
-2
-3
-4
2
3
2
3
4
5
4
-1
-2
-3
-4
-5
0
A
(4,3)
如何表示点A的位置:
过点A作x轴的垂线,垂足在x轴上对
应的数是4,就是点A的横坐标.
过点A作y轴的垂线,垂足在y轴上对
应的数是3,就是点A的纵坐标.
有序数对(4,3)就是点A的坐标.
x
y
x轴上的坐标
写在前面
·
B
3
1
4
2
5
-2
-4
-1
-3
0
1
2
3
4
5
-4
-3
-2
-1
x
横轴
y
纵轴
·
C
·
A
·
E
·
D
( 2,3 )
( 3,2 )
( -2,1 )
( -4,- 3 )
( 1,- 2 )
坐标是有序
的实数对.
写出图中A、B、C、D、E各点的坐标.
即学即练
x
O
1
2
3
-1
-2
-3
1
2
-1
-2
-3
y
在平面直角坐标系中找到表示A(3,-2)的点.
2.由坐标找点
由坐标找点的方法:
先找到表示横坐标与纵坐标的点,
然后过这两点分别作x轴与y轴的垂线,
垂线的交点就是该坐标对应的点。
A
(2,-3)
在平面直角坐标系中描出下列各点,
A(5,2) 、B(0,5)、C(2,-3)、 D(-2,-3)
A
·
B
·
D
·
(0,5)
0
1
2
3
4
5
-4
-3
-2
-1
3
1
4
2
5
-2
-4
-1
-3
y
纵轴
x
横轴
C
·
(5,2)
(-2,-3)
即学即练
(1)写出图中的平行四边形ABCD各个顶点的坐标.
(2)图中A与D,B与C的纵坐标相同吗? 为什么?
(3)A与B,C与D的横坐标相同吗?为什么?
x
y
0
1
1
A
B
C
D
(-2,3)
(-3,-1)
(3,-1)
(4,3)
合作探究
探究各坐标轴上、象限内的点的特征.
(1)各坐标轴上的点的坐标有什么特征?
(2)各象限内的点的符号有什么特点?
合作探究
O
y
x
-4 -3 -2 -1 1 2 3 4
3
2
1
-1
-2
-3
A
B
C
D
E
F
C (4,0)
A (-3,0)
B (1,0)
D (0,3)
E (0,2)
F (0,-2)
y 轴上的点的横坐标或纵坐标有什么特点?
x 轴上的点的横坐标或纵坐标有什么特点?
x 轴上的点,纵坐标为0.
y轴上的点,横坐标为0.
记为( x,0)
记为(0,y)
合作探究
观察坐标系,填写各象限内的点的坐标的特征:
点的位置 横坐标的符号 纵坐标的
符号
第一象限
第二象限
第三象限
第四象限
+
+
+
-
-
-
+
-
A
y
O
x
-1
-2
-3
-1
-2
-3
-4
1
2
3
4
1
2
3
4
5
-4
B
C
D
E
交流:不看平面直角坐标系,你能迅速说出A(4,5) , B(-2,3), C(-4,
-1), D(2.5,-2), E(0,-4)所在的象限吗?你的方法又是什么?
合作探究
建立坐标系求图形中点的坐标
问题:正方形ABCD的边长为4,请建立一个平面直角坐标系,并写出正方形的四个顶点A,B,C,D在这个平面直角坐标系中的坐标.
A
B
C
D
典型例题
4
4
y
x
(A)
B
C
D
解:如图,以顶点A为原点,AB所在直线为x轴,AD所在直线为y轴建立平面直角坐标系.
此时,正方形四个顶点A,B,C,D的坐标分别为:
A(0,0), B(4,0),
C(4,4), D(0,4).
O
典型例题
A
B
C
D
A(0,-4), B(4,-4),C(4,0), D(0,0).
y
x
O
想一想:还可以建立其他平面直角坐标系,表示正方形的四个顶点A,B,C,D的坐标吗?
A(-4,0), B(0,0),C(0,4), D(-4,4).
A(-4,-4), B(0,-4),C(0,0), D(-4,0).
A(-2,-2), B(2,-2),C(2,2), D(-2,2).
典型例题
追问 由上得知,建立的平面直角坐标系不同,则各点的坐标也不同.你认为怎样建立直角坐标系才比较适当?
【总结】建立平面直角坐标系,一般要使图形上的点的坐标容易确定,例如以正方形的两条边所在的直线为坐标轴,建立平面直角坐标系,又如以正方形的中心为原点建立平面直角坐标系.需要说明的是,虽然建立不同的平面直角坐标系,同一个点会有不同的坐标,但正方形的形状和性质不会改变.
方法总结
x
y
0
.A(2,1)
.B(2,-1)
.C(-2,1)
E(3,0)
D(0,1)
.F(-2,-1)
1
-1
1、能够正确画出直角坐标系.
2、能在直角坐标系中,根据坐标找出点, 由点求出坐标.
3、掌握x轴,y轴上点的坐标的特点:
x轴上的点的纵坐标为0,表示为(x,0)
y轴上的点的横坐标为0,表示为(0,y)
4.当两点的横坐标相同,纵坐标互为相反数时,这两点关于X轴对称;当两点的纵坐标相同,横坐标互为相反数时,这两点关于Y轴对称;当两点的横坐标、纵坐标互为相反数时,这两点关于原点对称;
课堂小结
1.已知坐标平面内点A(m,n)在第四象限,那么点B(n,m)在( )
A.第一象限 B.第二象限.
C.第三象限 D.第四象限
B
检测目标
2、在直角坐标系中描下列各点:
A(4,3),
B(-2,3),
C(-4,-1),
D(2,-2).
3
1
4
2
5
-2
-1
-3
0
1
2
3
4
5
-4
-3
-2
-1
x
y
·
B
·
A
·
D
·
C
检测目标
3、请你根据下列各点的坐标判定它们分别在第几象限或在什么坐标轴上?
A(-5、2) B(3、-2) C(0、4), D(-6、0) E(1、8) F(0、0), G(5、0),H(-6、-4)K(0、-3)
解:A在第二象限,
B在第四象限,
C在Y的正半轴,
E在第一象限,
D在X轴的负半轴,
F在原点,
G在X轴的正半轴,
H在第三象限,
K在Y轴的负半轴。
检测目标
4.如果同一直角坐标系下两个点的横坐标相同,那么过这两点的直线( )
(A)平行于x轴
(B)平行于y轴
(C)经过原点
(D)以上都不对
B
检测目标
我们已经站在了人生的起跑线上,为了实现心中的远大目标,我们正努力拼搏着。成功属于不畏困难、勇往直前的人。相信自己!
教师寄语
通过本课学习,你收获了什么?
课后作业:
完成教科书中相关练习题。
名言欣赏:
数学是打开科学大门的钥匙。
——培根
有序数对
有顺序的两个数a与b组成的数对叫 做有序数对,记作(a,b)。
(a,b)与(b,a)表示 的是两个不同的位置。
有序数对
点的位置
思想方法:
知识点:
注意点:
相互转化
数形结合
知识回顾
0
-5
-4
-3
-2
-1
1
2
3
4
5
6
-6
7
数轴上的点可以用一个数来表示,这个数叫做这个点在数轴上的坐标. 例如点A在数轴上的坐标为-3,点B在数轴上的坐标为2。反过来,知道数轴上一个点的坐标,这个的点在数轴上的位置也就确定了。
A
B
如何确定数轴上点的位置?
1米
知识回顾
雁塔
中心广场
钟楼
大成殿
科技大学
碑林
影月湖
如图,是某城市旅游景点的示意图。你要如何确定各个景点的位置?
如何确定平面上点的位置?
7.1.2 平面直角坐标系
人教版七年级数学 下册
目标导航
1.知道平面直角坐标系的相关概念.
2.学会建立平面直角坐标系.
3.已知平面直角坐标系中的点,能说出它的坐标;已知点的坐标,能在平面直角坐标系中描出表示该坐标的点.
认真阅读课本中7.1.2 平面直角坐标系的内容,完成下面任务。
自主研学
学习任务:
1.如何确定一个点在数轴上的位置.
2.平面直角坐标系的概念,如何建立平面直角坐标系,象限划分.
根据点在数轴上的坐标可以直接确定该点在数轴上的位置.
1
2
3
-1
-2
-3
O
1
-1
2
-2
-3
3
x
y
x轴
横轴
y轴
纵轴
直角坐标
系的原点
在平面内,两条互相垂直、原点重合的数轴,组成平面直角坐标系.
水平
位置
竖直
位置
x轴(横轴)
y轴(纵轴)
两坐标轴的交点为平面直角坐标系的原点
坐标轴
知识归纳
3
1
4
2
5
-2
-4
-1
-3
0
1
2
3
4
5
-4
-3
-2
-1
x
横轴
y
纵轴
原点
第Ⅰ象限
第Ⅳ象限
第Ⅲ象限
第Ⅱ象限
注 意:坐标轴上的点不属于任何象限.
知识归纳
·
A
3
1
4
2
5
-2
-4
-1
-3
0
1
2
3
4
5
-4
-3
-2
-1
x
横轴
y
纵轴
A点在x 轴上的坐标为4
A点在y 轴上的坐标为2
A点在平面直角坐标系中的坐标为(4, 2)
记作:A(4,2)
X轴上的坐标
写在前面
·
B
B(-4,1)
知识归纳
x
O
下面四个图形中,是平面直角坐标系的是( )
-3 -2 -1 1 2 3
3
2
1
-1
-2
-3
y
x
x
y
(A)
3 2 1 -1 -2 -3
x
y
(B)
2
1
-1
-2
O
-3 -2 -1 1 2 3
3
2
1
-1
-2
-3
(C)
O
-3 -2 -1 1 2 3
3
2
1
-1
-2
-3
y
(D)
O
D
即学即练
1.由点找坐标:
如何表示点A的位置?
1
1
-1
-2
-3
-4
2
3
2
3
4
5
4
-1
-2
-3
-4
-5
0
A
(4,3)
如何表示点A的位置:
过点A作x轴的垂线,垂足在x轴上对
应的数是4,就是点A的横坐标.
过点A作y轴的垂线,垂足在y轴上对
应的数是3,就是点A的纵坐标.
有序数对(4,3)就是点A的坐标.
x
y
x轴上的坐标
写在前面
·
B
3
1
4
2
5
-2
-4
-1
-3
0
1
2
3
4
5
-4
-3
-2
-1
x
横轴
y
纵轴
·
C
·
A
·
E
·
D
( 2,3 )
( 3,2 )
( -2,1 )
( -4,- 3 )
( 1,- 2 )
坐标是有序
的实数对.
写出图中A、B、C、D、E各点的坐标.
即学即练
x
O
1
2
3
-1
-2
-3
1
2
-1
-2
-3
y
在平面直角坐标系中找到表示A(3,-2)的点.
2.由坐标找点
由坐标找点的方法:
先找到表示横坐标与纵坐标的点,
然后过这两点分别作x轴与y轴的垂线,
垂线的交点就是该坐标对应的点。
A
(2,-3)
在平面直角坐标系中描出下列各点,
A(5,2) 、B(0,5)、C(2,-3)、 D(-2,-3)
A
·
B
·
D
·
(0,5)
0
1
2
3
4
5
-4
-3
-2
-1
3
1
4
2
5
-2
-4
-1
-3
y
纵轴
x
横轴
C
·
(5,2)
(-2,-3)
即学即练
(1)写出图中的平行四边形ABCD各个顶点的坐标.
(2)图中A与D,B与C的纵坐标相同吗? 为什么?
(3)A与B,C与D的横坐标相同吗?为什么?
x
y
0
1
1
A
B
C
D
(-2,3)
(-3,-1)
(3,-1)
(4,3)
合作探究
探究各坐标轴上、象限内的点的特征.
(1)各坐标轴上的点的坐标有什么特征?
(2)各象限内的点的符号有什么特点?
合作探究
O
y
x
-4 -3 -2 -1 1 2 3 4
3
2
1
-1
-2
-3
A
B
C
D
E
F
C (4,0)
A (-3,0)
B (1,0)
D (0,3)
E (0,2)
F (0,-2)
y 轴上的点的横坐标或纵坐标有什么特点?
x 轴上的点的横坐标或纵坐标有什么特点?
x 轴上的点,纵坐标为0.
y轴上的点,横坐标为0.
记为( x,0)
记为(0,y)
合作探究
观察坐标系,填写各象限内的点的坐标的特征:
点的位置 横坐标的符号 纵坐标的
符号
第一象限
第二象限
第三象限
第四象限
+
+
+
-
-
-
+
-
A
y
O
x
-1
-2
-3
-1
-2
-3
-4
1
2
3
4
1
2
3
4
5
-4
B
C
D
E
交流:不看平面直角坐标系,你能迅速说出A(4,5) , B(-2,3), C(-4,
-1), D(2.5,-2), E(0,-4)所在的象限吗?你的方法又是什么?
合作探究
建立坐标系求图形中点的坐标
问题:正方形ABCD的边长为4,请建立一个平面直角坐标系,并写出正方形的四个顶点A,B,C,D在这个平面直角坐标系中的坐标.
A
B
C
D
典型例题
4
4
y
x
(A)
B
C
D
解:如图,以顶点A为原点,AB所在直线为x轴,AD所在直线为y轴建立平面直角坐标系.
此时,正方形四个顶点A,B,C,D的坐标分别为:
A(0,0), B(4,0),
C(4,4), D(0,4).
O
典型例题
A
B
C
D
A(0,-4), B(4,-4),C(4,0), D(0,0).
y
x
O
想一想:还可以建立其他平面直角坐标系,表示正方形的四个顶点A,B,C,D的坐标吗?
A(-4,0), B(0,0),C(0,4), D(-4,4).
A(-4,-4), B(0,-4),C(0,0), D(-4,0).
A(-2,-2), B(2,-2),C(2,2), D(-2,2).
典型例题
追问 由上得知,建立的平面直角坐标系不同,则各点的坐标也不同.你认为怎样建立直角坐标系才比较适当?
【总结】建立平面直角坐标系,一般要使图形上的点的坐标容易确定,例如以正方形的两条边所在的直线为坐标轴,建立平面直角坐标系,又如以正方形的中心为原点建立平面直角坐标系.需要说明的是,虽然建立不同的平面直角坐标系,同一个点会有不同的坐标,但正方形的形状和性质不会改变.
方法总结
x
y
0
.A(2,1)
.B(2,-1)
.C(-2,1)
E(3,0)
D(0,1)
.F(-2,-1)
1
-1
1、能够正确画出直角坐标系.
2、能在直角坐标系中,根据坐标找出点, 由点求出坐标.
3、掌握x轴,y轴上点的坐标的特点:
x轴上的点的纵坐标为0,表示为(x,0)
y轴上的点的横坐标为0,表示为(0,y)
4.当两点的横坐标相同,纵坐标互为相反数时,这两点关于X轴对称;当两点的纵坐标相同,横坐标互为相反数时,这两点关于Y轴对称;当两点的横坐标、纵坐标互为相反数时,这两点关于原点对称;
课堂小结
1.已知坐标平面内点A(m,n)在第四象限,那么点B(n,m)在( )
A.第一象限 B.第二象限.
C.第三象限 D.第四象限
B
检测目标
2、在直角坐标系中描下列各点:
A(4,3),
B(-2,3),
C(-4,-1),
D(2,-2).
3
1
4
2
5
-2
-1
-3
0
1
2
3
4
5
-4
-3
-2
-1
x
y
·
B
·
A
·
D
·
C
检测目标
3、请你根据下列各点的坐标判定它们分别在第几象限或在什么坐标轴上?
A(-5、2) B(3、-2) C(0、4), D(-6、0) E(1、8) F(0、0), G(5、0),H(-6、-4)K(0、-3)
解:A在第二象限,
B在第四象限,
C在Y的正半轴,
E在第一象限,
D在X轴的负半轴,
F在原点,
G在X轴的正半轴,
H在第三象限,
K在Y轴的负半轴。
检测目标
4.如果同一直角坐标系下两个点的横坐标相同,那么过这两点的直线( )
(A)平行于x轴
(B)平行于y轴
(C)经过原点
(D)以上都不对
B
检测目标
我们已经站在了人生的起跑线上,为了实现心中的远大目标,我们正努力拼搏着。成功属于不畏困难、勇往直前的人。相信自己!
教师寄语
通过本课学习,你收获了什么?
课后作业:
完成教科书中相关练习题。
