1.1 探究动量变化与冲量的关系(共30张PPT)
文档属性
| 名称 | 1.1 探究动量变化与冲量的关系(共30张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 1.3MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 物理 | ||
| 更新时间 | 2020-02-12 00:00:00 | ||
图片预览







文档简介
(共30张PPT)
1.1探究动量变化与冲量的关系
鸡蛋从一米多高的地方落到地板上,肯定会被打破,而在地板上放一块泡沫塑料垫,让鸡蛋落到泡沫塑料上,鸡蛋就不会被打破。
为什么软包装、“软着陆”对物体的破坏力小?
力对物体在时间上的累积效应与运动状态的改变
从而:
揭示了一个物理规律:动量定理
以上过程即为动量定理的推导
1、动量 P
1)定义:运动物体的质量m和速度v的乘积叫做物体的动量。
一、两个相关概念
2)特点说明:
(1)矢量性:方向与该时刻速度的方向相同
单位:千克·米/秒,( kg·m/s)
(2)动量P是状态量:与某时刻物体的m和v对应
(3)相对性:v与参考系选择有关,常以地面为参考系。
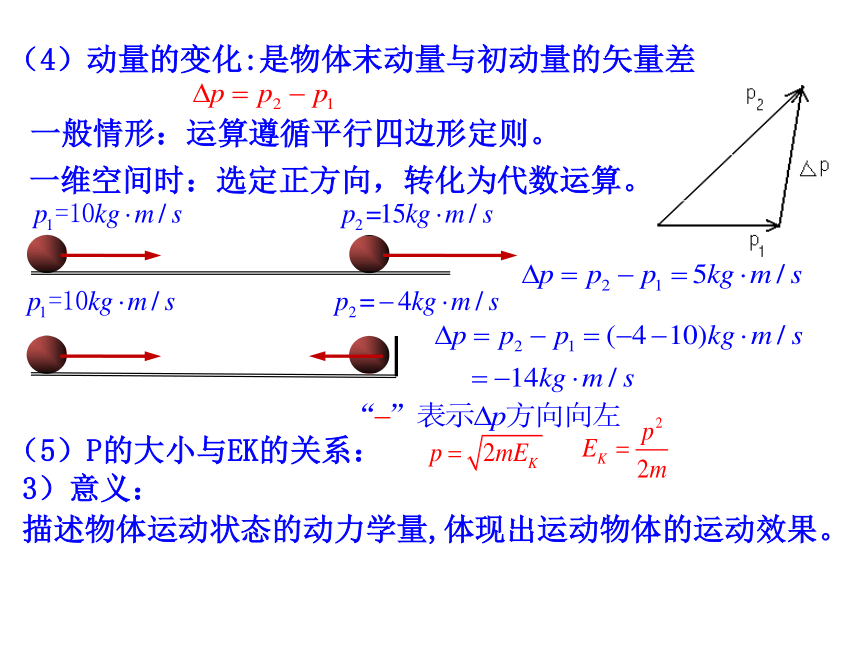
一般情形:运算遵循平行四边形定则。
(5)P的大小与EK的关系:
3)意义:
描述物体运动状态的动力学量,体现出运动物体的运动效果。
(4)动量的变化:是物体末动量与初动量的矢量差
一维空间时:选定正方向,转化为代数运算。
例1、在水平面上有甲、乙两滑块,其质量分别为m1=1.0kg和m2=2.0kg,且沿同一直线运动,若以甲运动的方向为正方向,由甲的速度υ1=10.0m/s,乙的速度υ2=-5.0m/s,甲的动量大小是 ,
方向 ;乙的动量大小是 ,方向 .
10.0kg·m/s
10.0kg·m/s
与甲运动方向相同
与甲运动方向相反
例2、一个质量为0.5kg的足球,以20m/s的速度向东运动,受到足球队员的作用力后,改为以20m/s的速度向西运动,足球在受足球队员作用前瞬间的动量p是多少?作用后瞬间的动量p?又是多少?足球的动量改变量Δp是多少?
以向东为正方向,
求一维空间物体的动量先要规定正方向,确定物体的动量的变化Δp,一定要注意到动量的方向性。
例3、一物体放在光滑的水平面上,有一颗子弹以水平速度υ0射向它,可能有三种情况:⑴子弹反弹回去;⑵子弹射中物体后留在物体中,二者以相同的速度一起运动;⑶子弹射穿物体后各以大小不同但方向相同的速度运动。在这三种情况中,子弹动量的改变量最大的是 种情况。
⑴
例4、质量为m的质点以速度υ绕半径R的圆周轨道做匀速圆周运动,在半个周期内动量的改变量大小为 ( )
A.0 B.mυ C.2mυ D.无法确定
C
例5、一个质量为2kg的物体以某一速度在空中水平抛出,飞行的时间为5s,求物体从抛出到落地过程中动量的变化量。不计空气阻力(重力加速度g=10m/s2)
物体做平抛运动,水平方向速度的变化量为零,即水平方向动量的变化也为零;在竖直方向,速度的变化量即为末速度,?υ=υ=gt=50m/s,物体动量变化量只有竖直方向的动量变化Δp= m?υ =100 kgm/s,方向竖直向下。
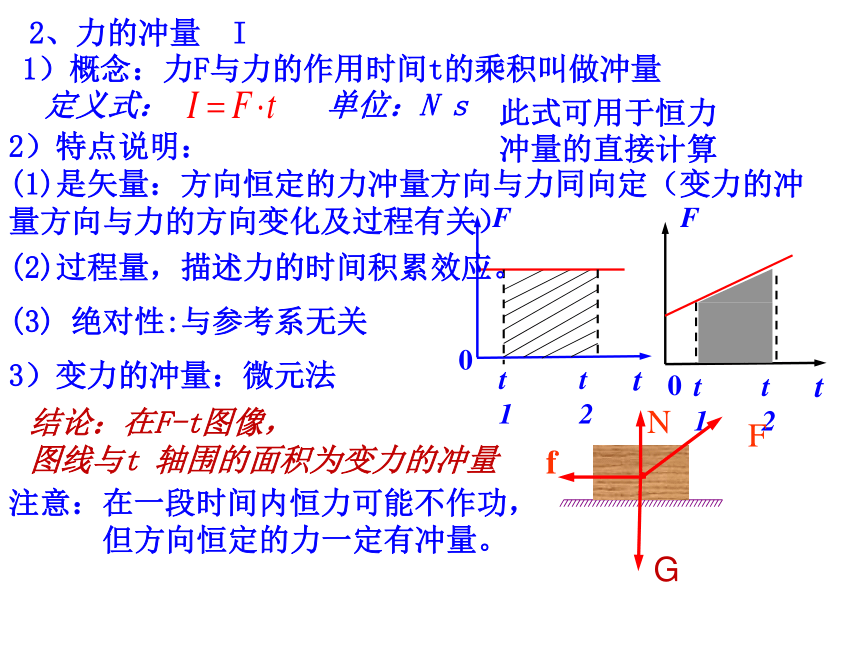
1)概念:力F与力的作用时间t的乘积叫做冲量
2、力的冲量 I
3)变力的冲量:微元法
结论:在F-t图像,
图线与t 轴围的面积为变力的冲量
2)特点说明:
(1)是矢量:方向恒定的力冲量方向与力同向定(变力的冲量方向与力的方向变化及过程有关)
注意:在一段时间内恒力可能不作功,
但方向恒定的力一定有冲量。
(2)过程量,描述力的时间积累效应。
(3) 绝对性:与参考系无关
此式可用于恒力冲量的直接计算
1、定理内容:物体所受合外力的冲量等于物体的动量变化。
1)冲量I是使物体动量P发生变化的原因和量度;
I是物体所受的合外力的冲量。
2)矢量式:为v的方向(注意一维方向的确定:规定正方向)。
二、动量定理
3)独立性:某方向的冲量只改变该方向上物体的动量。
4)广泛性:适用于恒力、变力(F平均值);适用于单个物体、物体系统。
2、说明:
三、动量定理的应用
例1:人从高处跳下,与地面接触时双腿弯曲,这样是为了( )
A、减少落地时的动量 B、减少动量的变化
C、减少冲量 D、减小地面对人的作用力
动量变化一定时,力作用时间越短,力就越大。
D
作用力一定时,力的作用时间越长,动量变化就越大。
例2:把重物压在纸带上,用一水平力缓缓拉动纸带,重物跟着
纸带一起运动;若迅速拉动纸带,纸带就会从重物下抽出,解
释这个现象的原因是 ( )
A、在缓缓拉动纸带时,纸带给重物的摩擦力大
B、在迅速拉动纸带时,纸带给重物的摩擦力大
C、在缓缓拉动纸带时,纸带给重物的冲量大
D、在迅速拉动纸带时,纸带给重物的冲量大
C
1、定性解释:
例3.蹦床是运动员在一张绷紧的弹性网上蹦跳、翻滚并做各种空中动作的运动项目。一个质量为60kg的运动员,从离水平网面3.2m高处自由下落,着网后沿竖直方向蹦回离水平网面5.0m高处。已知运动员与网接触的时间为1.2s。求这段时间内网对运动员的平均作用力。(g取10m/s2)
2、定量计算:
例2、如图,用0.5kg的铁锤把钉子钉进木头里去,打击时铁锤的速度v=4.0m/s,如果打击后铁锤的速度变为零,打击的作用时间是0.01s,求铁锤钉钉子的平均作用力。
解析:取铁锤作为研究对象,铁锤受到钉子的作用力为F,取竖直向下为正方向,则由动量定理得:
即铁锤受到的作用力大小为205N,方向向上;
由牛顿第三定律,铁锤钉钉子的平均作用力为205N,
方向竖直向下。
3、思路归纳:利用动量定理解题步骤:
⑴明确对象和过程;
⑵分析受力和状态;
⑶规定正方向,确定物理量;
(4)依据规律建方程;仔细求解得结果。
答案:I= ΔP=2mv.
思考1:质量为m的物体,沿半径为R的轨道以速率v做匀速圆周运动。(向心力的大小时多少?周期是多少?)求物体所受的合外力在半周期内的冲量。
思考2:以速度V0水平抛出一个质量为1kg的物体,若在抛出后5s钟落地,求它后3s内动量的变化。
答案:ΔP=mgt=30kgm/s
推论:抛体运动中在相等的时间里物体的速度变化量都相等
基本题型:1)利用动量变化求冲量2)利用冲量求动量变化
4、全程处理和分段处理方法的应用
例1.质量为m的小球,从沙坑上方自由下落,经t1到达
沙坑表面,又经t2停在沙坑里,如图所示,求:
(1) 沙对小球的平均阻力F;
(2) 小球在沙坑里下落过程所受的总冲量I.
例3.一质量为m的小球,以初速度v0 沿水平方向射出,恰好垂直地射到一倾角为30° 的固定斜面上,并立即反方向弹回。已知反弹速度的大小是入射速度大小的3/4,求在碰撞中斜面对小球的冲量大小
解:小球做平抛运动.设碰撞斜面时速度为v,v 的方向与竖直线的夹角为30°,且水平分量仍为v0。
碰撞过程中,小球速度由v变为反向的3v/4,
由①、②得
取垂直斜面向上为正方向
碰撞时间极短,可不计重力的冲量,
由动量定理,斜面对小球的冲量为
1.动量是状态量:公式p=mv中的速度v是瞬时速度。
考查要点一:对动量和动量变化量的理解
题型和解法
2.动量是矢量:如果在一条直线上运动,可以选定一个正方向,其正负就容易确定了。
3.动量具有相对性:通常在不指明的情况下,物体的动量是指物体相对地面的动量。
5.动量和动能的关系
(1) 动量是矢量,动能是标量。速度变化时,动量一定变化,但动能不一定变化;动能变化时,速度一定变化,动量一定变化。
练习.物体在运动过程中加速度不为零,则下列说法正确的是 ( )
A.物体速度的大小一定随时间变化
B.物体速度的方向一定随时间变化
C.物体动能一定随时间变化
D.物体动量一定随时间变化
D
点拨:物体的加速度不为零时,速度的大小不一定变化,如匀速圆周运动
1.对冲量的理解
(1)冲量是过程量:反映作用在物体上的力对时间的积累效应;
考查要点二:对冲量理解及计算
2.冲量的计算
(1)力的冲量:仅由该力的大小和作用时间共同决定,与其他力是否存在及物体的运动状态无关;
(2) 冲量是矢量:若力的方向不变,冲量的方向与力的方向相同;
(3)冲量的绝对性:冲量仅由力和时间两个因素决定,具有绝对性。
(2)求合冲量:如果是一维情形,可以化为代数和,如果不在一条直线上,求合冲量遵循平行四边形定则或用正交分解法求出。
(3)变力的冲量可用动量定理求解。
若力的方向变化,冲量的方向与相应时间动量变化量的方向相同。
2.如图,一质量m=3 kg的物体静止在光滑水平面上,受到与水平方向成60°角的力作用,F的大小为9 N,经2 s时间,求:(取g=10 N/kg)
(1)物体重力冲量大小;(2)物体受到的支持力冲量大小;
(3)力F的冲量大小; (4)合外力的冲量大小。
受力分析,冲量公式。
解:(1)重力的冲量: IG=mgt=3×10×2 N·s=60 N·s
(3)力F的冲量IF=Ft=9×2 N·s=18 N·s
注意:
(1)冲量是一个过程量,学习冲量必须明确研究对象和作用过程,
(2)某个力的冲量的方向与合力的冲量方向不一定相同。
(1)定性解释有关现象:
①物体的动量变化量一定时,此时力的作用时间越短,力就越大;力的作用时间越长,力就越小。
②作用力一定时,此时力的作用时间越长,动量变化量越大;力的作用时间越短,动量变化量越小。
(2)定量计算的一般步骤:
①确定研究对象,明确运动过程。
②进行受力分析,分析确定每个力的冲量,并求出合力的冲量。
③选定正方向,确定初、末状态的动量及物体动量的变化量。
④根据动量定理列方程求解。
考查要点三:对动量定理的理解及应用
3.为了检测篮球的性能,某同学多次让一篮球从h1=1.8 m处自由下落,测出篮球从开始下落至第一次反弹到最高点所用时间为t=1.3 s,该篮球第一次反弹从离开地面至最高点所用时间为t2=0.5 s,篮球的质量为m=0.6 kg,g 取10 m/s2。求篮球对地面的平均作用力(不计空气阻力)。
解:设球从h1处下落触地的时间为t1,触地时速度大小为v1,弹起时速度大小为v2,弹起至达到最高点的时间为t2,
注意:篮球的运动分为三个阶段:下落、与地面作用、上升
注意
(1)在应用动量定理解题时,一定要对物体认真进行受力分析,不可有力的遗漏;建立方程时要事先选定正方向;对于变力的冲量,往往通过动量定理来计算;只有当相互作用时间Δt极短时,且相互作用力远大于重力时,才可舍去重力。
(2)若物体运动包括几个不同的过程,可对其中的一个阶段应用动量定理列方程,也可以对整个过程应用动量定理列方程,但表达式I=Δp中的I与Δp分别与该过程的总冲量与动量变化量相对应。
1.下列说法正确的是 ( )?
A.一质点受两个力的作用而处于平衡状态(静止或匀速直线运动),则这两个力在同一作用时间内的冲量一定相同
B.一质点受两个力的作用而处于平衡状态,则这两个力在同一时间内做的功都为零,或者一个做正功,一个做负功,且功的绝对值相等
C.在同一时间内作用力和反作用力的冲量一定大小相等,方向相反
D.在同一时间内作用力和反作用力有可能都做正功
BCD
配套练习
BC
4.如图所示,A、B两物体质量分别为mA、mB且mA>mB,置于光滑水平面上,相距较远.将两个大小均为F的力,同时分别作用在A、B上经相同距离后,撤去两个力,两物体发生碰撞并粘在一起后将 ( )
A.停止运动 B.向左运动
C.向右运动 D.不能确定
3.质量分别为m1和m2的两个物体(m1>m2),在光滑的水平面上沿同方向运动,具有相同的初动能.与运动方向相同的水平力F分别作用在这两个物体上,经过相同的时间后,两个物体的动量和动能的大小分别为P1、P2和E1、E2,则 ( )?
A.P1>P2和E1>E2 B.P1>P2和E1<E2
C.P1<P2和E1>E2 D.P1<P2和E1<E2?
B
C
5、如图,物体A和B用轻绳相连,挂在弹簧下静止不动,A、B的质量分别为m和M。当连接A、B的轻绳突然断开后,物体上升经某一位置时的速度为V,此时物体B下落的速度大小为u,那么在这段时间里弹簧的的弹力对物体A的冲量为 ( )
A.mV B.mV-Mu
C.mV+Mu D.m?(V+u)
D
6.如图所示,质量为M=4kg的木板长L=1.4m,静止在光滑的水平地面上,其上端右侧静置一个质量为m=1kg的小滑块,小滑块与木板间的动摩擦因数为μ=0.4.今用一水平力F=28N向右拉木板,要使小滑块从木板上掉下来,求此力至少作用多长时间?(重力加速度g取10m/s2)
分析过程:整个过程中,小滑块向右做初速为零的匀加速直线运动.
解:设拉力F作用的最短时间为t,撤去拉力前木板的位移为s0,小滑块滑到木板左端并恰好与木板达到的共同速度为v.
整个过程对系统由动量定理得:
撤去拉力F前木板的位移为:
整个过程对系统由功能关系得:
联立以上各式,代入已知数据求得:t=1s.
撤去拉力F前,木板向右做初速为零的
匀加速直线运动;撤去拉力F后,木板向右
做匀减速直线运动.要使小滑块从木板上掉
下来,拉力F作用的最短时间对应的过程是:
小滑块滑到木板左端时恰好与木板保持相对静止(即与木板达到共同的速度
1.1探究动量变化与冲量的关系
鸡蛋从一米多高的地方落到地板上,肯定会被打破,而在地板上放一块泡沫塑料垫,让鸡蛋落到泡沫塑料上,鸡蛋就不会被打破。
为什么软包装、“软着陆”对物体的破坏力小?
力对物体在时间上的累积效应与运动状态的改变
从而:
揭示了一个物理规律:动量定理
以上过程即为动量定理的推导
1、动量 P
1)定义:运动物体的质量m和速度v的乘积叫做物体的动量。
一、两个相关概念
2)特点说明:
(1)矢量性:方向与该时刻速度的方向相同
单位:千克·米/秒,( kg·m/s)
(2)动量P是状态量:与某时刻物体的m和v对应
(3)相对性:v与参考系选择有关,常以地面为参考系。
一般情形:运算遵循平行四边形定则。
(5)P的大小与EK的关系:
3)意义:
描述物体运动状态的动力学量,体现出运动物体的运动效果。
(4)动量的变化:是物体末动量与初动量的矢量差
一维空间时:选定正方向,转化为代数运算。
例1、在水平面上有甲、乙两滑块,其质量分别为m1=1.0kg和m2=2.0kg,且沿同一直线运动,若以甲运动的方向为正方向,由甲的速度υ1=10.0m/s,乙的速度υ2=-5.0m/s,甲的动量大小是 ,
方向 ;乙的动量大小是 ,方向 .
10.0kg·m/s
10.0kg·m/s
与甲运动方向相同
与甲运动方向相反
例2、一个质量为0.5kg的足球,以20m/s的速度向东运动,受到足球队员的作用力后,改为以20m/s的速度向西运动,足球在受足球队员作用前瞬间的动量p是多少?作用后瞬间的动量p?又是多少?足球的动量改变量Δp是多少?
以向东为正方向,
求一维空间物体的动量先要规定正方向,确定物体的动量的变化Δp,一定要注意到动量的方向性。
例3、一物体放在光滑的水平面上,有一颗子弹以水平速度υ0射向它,可能有三种情况:⑴子弹反弹回去;⑵子弹射中物体后留在物体中,二者以相同的速度一起运动;⑶子弹射穿物体后各以大小不同但方向相同的速度运动。在这三种情况中,子弹动量的改变量最大的是 种情况。
⑴
例4、质量为m的质点以速度υ绕半径R的圆周轨道做匀速圆周运动,在半个周期内动量的改变量大小为 ( )
A.0 B.mυ C.2mυ D.无法确定
C
例5、一个质量为2kg的物体以某一速度在空中水平抛出,飞行的时间为5s,求物体从抛出到落地过程中动量的变化量。不计空气阻力(重力加速度g=10m/s2)
物体做平抛运动,水平方向速度的变化量为零,即水平方向动量的变化也为零;在竖直方向,速度的变化量即为末速度,?υ=υ=gt=50m/s,物体动量变化量只有竖直方向的动量变化Δp= m?υ =100 kgm/s,方向竖直向下。
1)概念:力F与力的作用时间t的乘积叫做冲量
2、力的冲量 I
3)变力的冲量:微元法
结论:在F-t图像,
图线与t 轴围的面积为变力的冲量
2)特点说明:
(1)是矢量:方向恒定的力冲量方向与力同向定(变力的冲量方向与力的方向变化及过程有关)
注意:在一段时间内恒力可能不作功,
但方向恒定的力一定有冲量。
(2)过程量,描述力的时间积累效应。
(3) 绝对性:与参考系无关
此式可用于恒力冲量的直接计算
1、定理内容:物体所受合外力的冲量等于物体的动量变化。
1)冲量I是使物体动量P发生变化的原因和量度;
I是物体所受的合外力的冲量。
2)矢量式:为v的方向(注意一维方向的确定:规定正方向)。
二、动量定理
3)独立性:某方向的冲量只改变该方向上物体的动量。
4)广泛性:适用于恒力、变力(F平均值);适用于单个物体、物体系统。
2、说明:
三、动量定理的应用
例1:人从高处跳下,与地面接触时双腿弯曲,这样是为了( )
A、减少落地时的动量 B、减少动量的变化
C、减少冲量 D、减小地面对人的作用力
动量变化一定时,力作用时间越短,力就越大。
D
作用力一定时,力的作用时间越长,动量变化就越大。
例2:把重物压在纸带上,用一水平力缓缓拉动纸带,重物跟着
纸带一起运动;若迅速拉动纸带,纸带就会从重物下抽出,解
释这个现象的原因是 ( )
A、在缓缓拉动纸带时,纸带给重物的摩擦力大
B、在迅速拉动纸带时,纸带给重物的摩擦力大
C、在缓缓拉动纸带时,纸带给重物的冲量大
D、在迅速拉动纸带时,纸带给重物的冲量大
C
1、定性解释:
例3.蹦床是运动员在一张绷紧的弹性网上蹦跳、翻滚并做各种空中动作的运动项目。一个质量为60kg的运动员,从离水平网面3.2m高处自由下落,着网后沿竖直方向蹦回离水平网面5.0m高处。已知运动员与网接触的时间为1.2s。求这段时间内网对运动员的平均作用力。(g取10m/s2)
2、定量计算:
例2、如图,用0.5kg的铁锤把钉子钉进木头里去,打击时铁锤的速度v=4.0m/s,如果打击后铁锤的速度变为零,打击的作用时间是0.01s,求铁锤钉钉子的平均作用力。
解析:取铁锤作为研究对象,铁锤受到钉子的作用力为F,取竖直向下为正方向,则由动量定理得:
即铁锤受到的作用力大小为205N,方向向上;
由牛顿第三定律,铁锤钉钉子的平均作用力为205N,
方向竖直向下。
3、思路归纳:利用动量定理解题步骤:
⑴明确对象和过程;
⑵分析受力和状态;
⑶规定正方向,确定物理量;
(4)依据规律建方程;仔细求解得结果。
答案:I= ΔP=2mv.
思考1:质量为m的物体,沿半径为R的轨道以速率v做匀速圆周运动。(向心力的大小时多少?周期是多少?)求物体所受的合外力在半周期内的冲量。
思考2:以速度V0水平抛出一个质量为1kg的物体,若在抛出后5s钟落地,求它后3s内动量的变化。
答案:ΔP=mgt=30kgm/s
推论:抛体运动中在相等的时间里物体的速度变化量都相等
基本题型:1)利用动量变化求冲量2)利用冲量求动量变化
4、全程处理和分段处理方法的应用
例1.质量为m的小球,从沙坑上方自由下落,经t1到达
沙坑表面,又经t2停在沙坑里,如图所示,求:
(1) 沙对小球的平均阻力F;
(2) 小球在沙坑里下落过程所受的总冲量I.
例3.一质量为m的小球,以初速度v0 沿水平方向射出,恰好垂直地射到一倾角为30° 的固定斜面上,并立即反方向弹回。已知反弹速度的大小是入射速度大小的3/4,求在碰撞中斜面对小球的冲量大小
解:小球做平抛运动.设碰撞斜面时速度为v,v 的方向与竖直线的夹角为30°,且水平分量仍为v0。
碰撞过程中,小球速度由v变为反向的3v/4,
由①、②得
取垂直斜面向上为正方向
碰撞时间极短,可不计重力的冲量,
由动量定理,斜面对小球的冲量为
1.动量是状态量:公式p=mv中的速度v是瞬时速度。
考查要点一:对动量和动量变化量的理解
题型和解法
2.动量是矢量:如果在一条直线上运动,可以选定一个正方向,其正负就容易确定了。
3.动量具有相对性:通常在不指明的情况下,物体的动量是指物体相对地面的动量。
5.动量和动能的关系
(1) 动量是矢量,动能是标量。速度变化时,动量一定变化,但动能不一定变化;动能变化时,速度一定变化,动量一定变化。
练习.物体在运动过程中加速度不为零,则下列说法正确的是 ( )
A.物体速度的大小一定随时间变化
B.物体速度的方向一定随时间变化
C.物体动能一定随时间变化
D.物体动量一定随时间变化
D
点拨:物体的加速度不为零时,速度的大小不一定变化,如匀速圆周运动
1.对冲量的理解
(1)冲量是过程量:反映作用在物体上的力对时间的积累效应;
考查要点二:对冲量理解及计算
2.冲量的计算
(1)力的冲量:仅由该力的大小和作用时间共同决定,与其他力是否存在及物体的运动状态无关;
(2) 冲量是矢量:若力的方向不变,冲量的方向与力的方向相同;
(3)冲量的绝对性:冲量仅由力和时间两个因素决定,具有绝对性。
(2)求合冲量:如果是一维情形,可以化为代数和,如果不在一条直线上,求合冲量遵循平行四边形定则或用正交分解法求出。
(3)变力的冲量可用动量定理求解。
若力的方向变化,冲量的方向与相应时间动量变化量的方向相同。
2.如图,一质量m=3 kg的物体静止在光滑水平面上,受到与水平方向成60°角的力作用,F的大小为9 N,经2 s时间,求:(取g=10 N/kg)
(1)物体重力冲量大小;(2)物体受到的支持力冲量大小;
(3)力F的冲量大小; (4)合外力的冲量大小。
受力分析,冲量公式。
解:(1)重力的冲量: IG=mgt=3×10×2 N·s=60 N·s
(3)力F的冲量IF=Ft=9×2 N·s=18 N·s
注意:
(1)冲量是一个过程量,学习冲量必须明确研究对象和作用过程,
(2)某个力的冲量的方向与合力的冲量方向不一定相同。
(1)定性解释有关现象:
①物体的动量变化量一定时,此时力的作用时间越短,力就越大;力的作用时间越长,力就越小。
②作用力一定时,此时力的作用时间越长,动量变化量越大;力的作用时间越短,动量变化量越小。
(2)定量计算的一般步骤:
①确定研究对象,明确运动过程。
②进行受力分析,分析确定每个力的冲量,并求出合力的冲量。
③选定正方向,确定初、末状态的动量及物体动量的变化量。
④根据动量定理列方程求解。
考查要点三:对动量定理的理解及应用
3.为了检测篮球的性能,某同学多次让一篮球从h1=1.8 m处自由下落,测出篮球从开始下落至第一次反弹到最高点所用时间为t=1.3 s,该篮球第一次反弹从离开地面至最高点所用时间为t2=0.5 s,篮球的质量为m=0.6 kg,g 取10 m/s2。求篮球对地面的平均作用力(不计空气阻力)。
解:设球从h1处下落触地的时间为t1,触地时速度大小为v1,弹起时速度大小为v2,弹起至达到最高点的时间为t2,
注意:篮球的运动分为三个阶段:下落、与地面作用、上升
注意
(1)在应用动量定理解题时,一定要对物体认真进行受力分析,不可有力的遗漏;建立方程时要事先选定正方向;对于变力的冲量,往往通过动量定理来计算;只有当相互作用时间Δt极短时,且相互作用力远大于重力时,才可舍去重力。
(2)若物体运动包括几个不同的过程,可对其中的一个阶段应用动量定理列方程,也可以对整个过程应用动量定理列方程,但表达式I=Δp中的I与Δp分别与该过程的总冲量与动量变化量相对应。
1.下列说法正确的是 ( )?
A.一质点受两个力的作用而处于平衡状态(静止或匀速直线运动),则这两个力在同一作用时间内的冲量一定相同
B.一质点受两个力的作用而处于平衡状态,则这两个力在同一时间内做的功都为零,或者一个做正功,一个做负功,且功的绝对值相等
C.在同一时间内作用力和反作用力的冲量一定大小相等,方向相反
D.在同一时间内作用力和反作用力有可能都做正功
BCD
配套练习
BC
4.如图所示,A、B两物体质量分别为mA、mB且mA>mB,置于光滑水平面上,相距较远.将两个大小均为F的力,同时分别作用在A、B上经相同距离后,撤去两个力,两物体发生碰撞并粘在一起后将 ( )
A.停止运动 B.向左运动
C.向右运动 D.不能确定
3.质量分别为m1和m2的两个物体(m1>m2),在光滑的水平面上沿同方向运动,具有相同的初动能.与运动方向相同的水平力F分别作用在这两个物体上,经过相同的时间后,两个物体的动量和动能的大小分别为P1、P2和E1、E2,则 ( )?
A.P1>P2和E1>E2 B.P1>P2和E1<E2
C.P1<P2和E1>E2 D.P1<P2和E1<E2?
B
C
5、如图,物体A和B用轻绳相连,挂在弹簧下静止不动,A、B的质量分别为m和M。当连接A、B的轻绳突然断开后,物体上升经某一位置时的速度为V,此时物体B下落的速度大小为u,那么在这段时间里弹簧的的弹力对物体A的冲量为 ( )
A.mV B.mV-Mu
C.mV+Mu D.m?(V+u)
D
6.如图所示,质量为M=4kg的木板长L=1.4m,静止在光滑的水平地面上,其上端右侧静置一个质量为m=1kg的小滑块,小滑块与木板间的动摩擦因数为μ=0.4.今用一水平力F=28N向右拉木板,要使小滑块从木板上掉下来,求此力至少作用多长时间?(重力加速度g取10m/s2)
分析过程:整个过程中,小滑块向右做初速为零的匀加速直线运动.
解:设拉力F作用的最短时间为t,撤去拉力前木板的位移为s0,小滑块滑到木板左端并恰好与木板达到的共同速度为v.
整个过程对系统由动量定理得:
撤去拉力F前木板的位移为:
整个过程对系统由功能关系得:
联立以上各式,代入已知数据求得:t=1s.
撤去拉力F前,木板向右做初速为零的
匀加速直线运动;撤去拉力F后,木板向右
做匀减速直线运动.要使小滑块从木板上掉
下来,拉力F作用的最短时间对应的过程是:
小滑块滑到木板左端时恰好与木板保持相对静止(即与木板达到共同的速度
同课章节目录
