陕西中考复习专题——几何探究型问题:“将军饮马”问题(第二讲,含答案)
文档属性
| 名称 | 陕西中考复习专题——几何探究型问题:“将军饮马”问题(第二讲,含答案) |  | |
| 格式 | zip | ||
| 文件大小 | 406.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 通用版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-02-13 14:07:05 | ||
图片预览


文档简介
几何探究型问题(针对第25题)
线段最值问题
类型一 “将军饮马”问题
模型3 “两定点+两定直线”型
问题 作法 图形 原理
在直线l1,l2上分别求点M,N,使四边形PQMN的周长最小 分别作点Q,P关于直线l1,l2的对称点Q′和P′,连接Q′P′,与两直线交点即为M,N 两点之间,线段最短.四边形PQMN周长的最小值为线段P′Q′+PQ的长
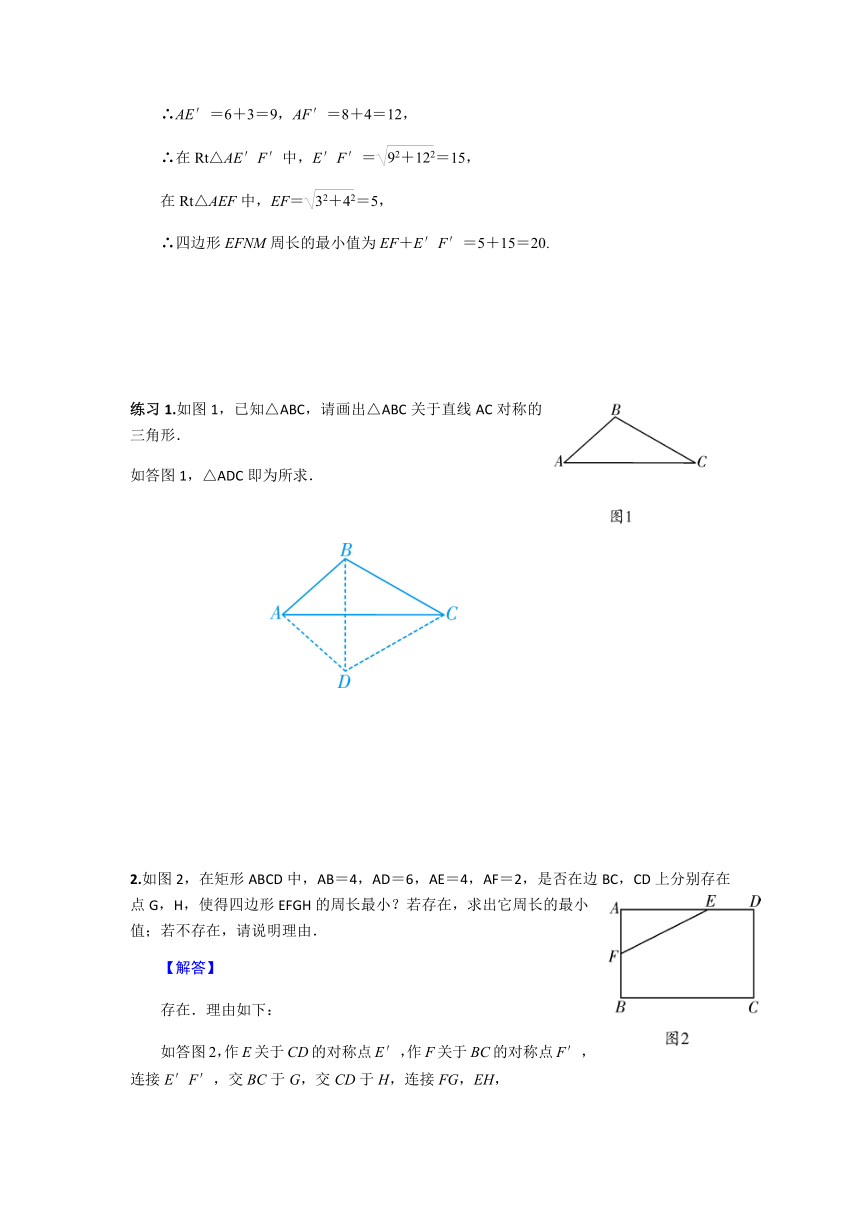
例题1.如图,在矩形ABCD中,AB=6,AD=8,E,F分别为边AB,AD的中点,点M,N分别为BC,CD上的动点,求四边形EFNM周长的最小值.
解:如答图,作点E关于BC的对称点E′,作点F关于CD的对称点F′,连接E′F′,交BC于M′,交CD于N′,连接EM′,FN′,则EM′=E′M′,FN′=F′N′,
∴EF+EM+MN+FN=EF+E′M′+M′N′+F′N′=EF+E′F′,
∴此时,四边形EFNM周长的最小值为EF+E′F′的长.
∵AB=6,AD=8,E,F分别为边AB,AD的中点,
∴AE′=6+3=9,AF′=8+4=12,
∴在Rt△AE′F′中,E′F′==15,
在Rt△AEF中,EF==5,
∴四边形EFNM周长的最小值为EF+E′F′=5+15=20.
练习1.如图1,已知△ABC,请画出△ABC关于直线AC对称的三角形.
如答图1,△ADC即为所求.
2.如图2,在矩形ABCD中,AB=4,AD=6,AE=4,AF=2,是否在边BC,CD上分别存在点G,H,使得四边形EFGH的周长最小?若存在,求出它周长的最小值;若不存在,请说明理由.
【解答】
存在.理由如下:
如答图2,作E关于CD的对称点E′,作F关于BC的对称点F′,连接E′F′,交BC于G,交CD于H,连接FG,EH,
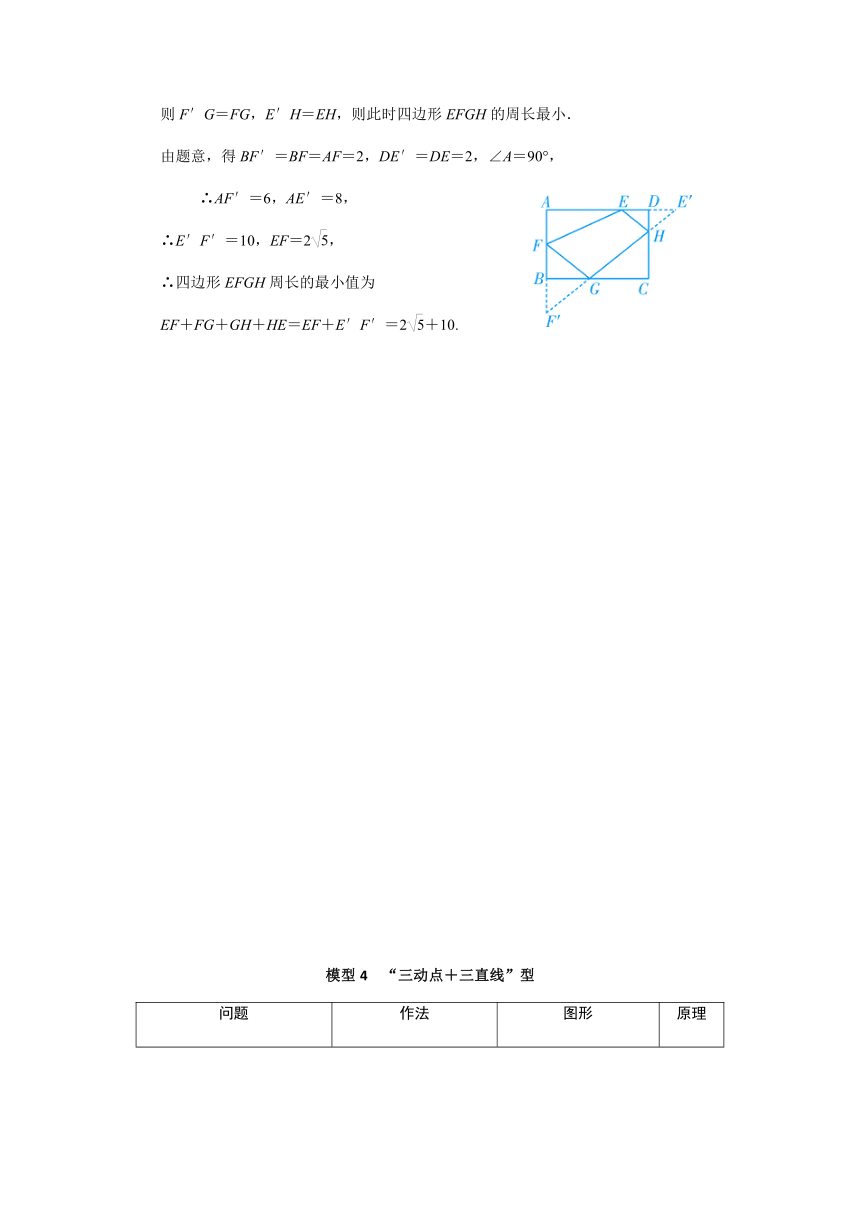
则F′G=FG,E′H=EH,则此时四边形EFGH的周长最小.
由题意,得BF′=BF=AF=2,DE′=DE=2,∠A=90°,
∴AF′=6,AE′=8,
∴E′F′=10,EF=2,
∴四边形EFGH周长的最小值为
EF+FG+GH+HE=EF+E′F′=2+10.
模型4 “三动点+三直线”型
问题 作法 图形 原理
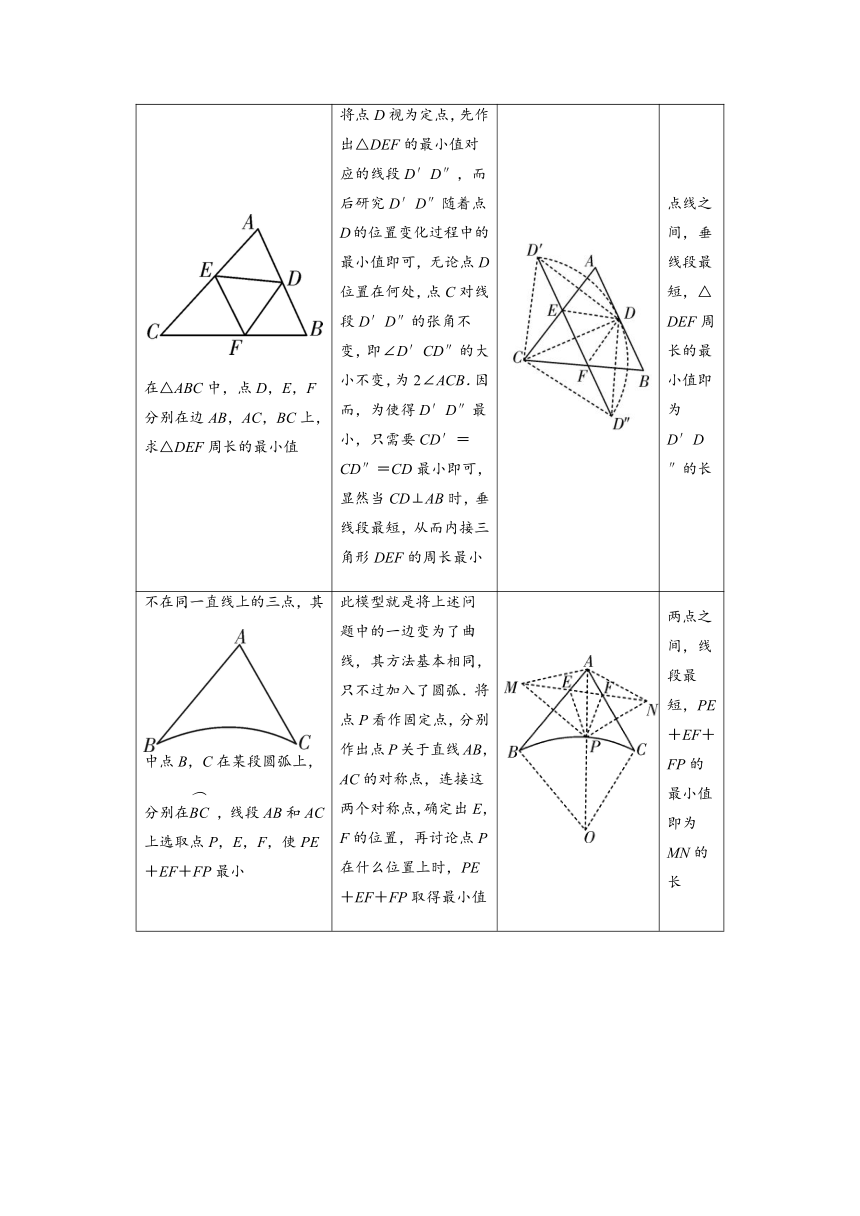
在△ABC中,点D,E,F分别在边AB,AC,BC上,求△DEF周长的最小值 将点D视为定点,先作出△DEF的最小值对应的线段D′D″,而后研究D′D″随着点D的位置变化过程中的最小值即可,无论点D位置在何处,点C对线段D′D″的张角不变,即∠D′CD″的大小不变,为2∠ACB.因而,为使得D′D″最小,只需要CD′=CD″=CD最小即可,显然当CD⊥AB时,垂线段最短,从而内接三角形DEF的周长最小 点线之间,垂线段最短,△DEF周长的最小值即为D′D″的长
不在同一直线上的三点,其中点B,C在某段圆弧上,分别在,线段AB和AC上选取点P,E,F,使PE+EF+FP最小 此模型就是将上述问题中的一边变为了曲线,其方法基本相同,只不过加入了圆弧.将点P看作固定点,分别作出点P关于直线AB,AC的对称点,连接这两个对称点,确定出E,F的位置,再讨论点P在什么位置上时,PE+EF+FP取得最小值 两点之间,线段最短,PE+EF+FP的最小值即为MN的长
例题1.如图1,在△ABC中,∠A=120°,AB=AC=5,则△ABC的外接圆半径R的值为______.
【解答】
如答图1,设O是△ABC外接圆的圆心,连接OA,OB,OC,∴OA=OB=OC.
∵∠BAC=120°,AB=AC=5,
∴△ABO是等边三角形,∴AB=OA=OB=5,
即△ABC的外接圆半径R的值为5.
2.如图2,⊙O的半径为13,弦AB=24,M是AB的中点,P是⊙O上一动点,求PM的最大值.
【解答】
如答图2,当PM⊥AB时,PM的值最大,
连接OA,由垂径定理可知AM=AB=12.
∵OA=13,∴由勾股定理可知OM=5,
∴PM=OM+OP=18.
3.如图3所示,AB,AC,是某新区的三条规划路,其中AB=6 km,AC=3 km,∠BAC=60°,所对的圆心角为60°,新区管委会想在路边建物资总站点P,在AB,AC路边分别建物资分站点E,F,也就是,分别在,线段AB和AC上选取点P,E,F.由于总站工作人员每天都要将物资在各物资站点间按P→E→F→P的路径进行运输,因此,要在各物资站点之间规划道路PE,EF和FP.为了快捷、环保和节约成本,要使得线段PE,EF,FP之和最短,试求PE+EF+FP的最小值.(各物资站点与所在道路之间的距离、路宽均忽略不计)
【解答】
如答图3,在上任取一点P,连接AP,分别以AB,AC所在直线为对称轴,作出点P关于AB的对称点M,点P关于AC的对称点N,连接MN,交AB于点E,交AC于点F,连接PE,PF,
易得AM=AP=AN,∠MAB=∠PAB,∠NAC=∠PAC,
∴∠BAC=∠PAB+∠PAC=∠MAB+∠NAC=60°,
∴∠MAN=120°,
∴M,P,N在以A为圆心,AP为半径的圆上.
设AP=r,易求得MN=r.
易得PE=ME,PF=FN,
∴PE+EF+PF=ME+EF+FN=MN=r,
∴当AP最小时,PE+EF+PF取得最小值.
连接BC,作出的圆心O,连接OA,OP,OB,OC.
∵AP+OP≥OA,
∴AP≥OA-OP,即点P在OA上时,AP可取得最小值.
设AB的中点为Q,连接QC,∴AQ=AC=3.
∵∠BAC=60°,∴AQ=QC=AC=BQ=3,
∴∠ABC=∠QCB=30°,∴∠ACB=90°,
∴由勾股定理可知BC=3.
∵∠BOC=60°,OB=OC=3,
∴△OBC是等边三角形,∴∠OBC=60°,
∴∠ABO=90°,∴由勾股定理可知OA=3.
∵OP=OB=3,∴AP=r=OA-OP=3-3,
∴PE+EF+PF=MN=r=3-9,
∴PE+EF+PF的最小值为(3-9)km.
课后作业
1.问题发现
(1)如图1,在△ABC中,AC=BC=2,∠ACB=90°,D是BC边的中点,E是AB边上一动点,则EC+ED的最小值是____;
问题研究
(2)如图2,平面直角坐标系中,分别以点A(-2,3),B(3,4)为圆心,以1,3为半径作⊙A,⊙B,M,N分别是⊙A,⊙B上的动点,P为x轴上的动点,试求PM+PN的最小值;
问题解决
(3)如图3,该图是某机器零件装置的模板,其外形是一个五边形,根据设计要求,边框AB的长为2米,边框BC长为3米,∠DAB=∠B=∠C=90°,联动杆DE长为2米,联动杆DE的两端D,E允许在AD,CE所在直线上滑动,点G恰好是DE的中点,点F可在边框BC上自由滑动,请确定该装置中的两根连接杆AF与FG长度和的最小值,并说明理由.
解:(1). 【解法提示】如答图1,作点C关于AB的对称点C′,连接C′B,DC′,与AB交于点E′,连接CE′,C′E,
∴CE′=C′E′,此时E′C+E′D=E′C′+E′D=C′D最短.
∵AC=BC=2,∠ACB=90°,
∴∠CBA=∠CAB=45°,C′B=CB=2,
∴∠C′BA=45°,∴∠DBC′=90°.
∵D是BC边的中点,∴DB=1.
在Rt△DBC′中,∵C′D2=12+22=5,∴C′D=,
∴EC+ED的最小值是.
(2)如答图2,作点B关于x轴的对称点B′,连接AB′,交⊙A于点M′,交x轴于点P′,连接P′B,交⊙B于点N′,则PM+PN的最小值为P′M′+P′N′=AB′-AM′-BN′.
∵B(3,4),∴B′(3,-4),
∴AB′==.
∵⊙A的半径为1,⊙B的半径为3,
∴AM′=1,BN′=3,
∴P′M′+P′N′=-1-3=-4,
∴PM+PN的最小值为-4.
答图
(3)如答图3,延长AD,CE,交于点H,连接GH.
∵∠DAB=∠B=∠C=90°,∴∠DHE=90°.
∵G是DE的中点,DE=2米,∴GE=DE=1(米).
∵联动杆DE的两端D,E允许在AD,CE所在直线上滑动,
∴点G在以H为圆心,1为半径的圆周上运动,
作点A关于BC的对称点A′,连接A′H,与BC交于点F′,与⊙H交于点G′,
此时AF+FG=A′F′+F′G′=A′G′为最短.
∵AB=2米,AH=BC=3米,A′B=2米,∴A′A=4米,
∴A′H==5(米),
∴A′G′=A′H-G′H=5-1=4(米),
∴该装置中的两根连接杆AF与FG长度的最小值为4米.
2.小敏在研究最值问题时遇到了这样的一个问题:如图1,在矩形ABCD中,AB=6,AD=8,E,F,G,H分别在矩形ABCD的边AD,AB,BC,CD上,则四边形EFGH的周长是否存在最小值?她决定按照老师讲的由特殊到一般逐步化归的思路去研究,请你帮助她完成下面的探究过程.
探究1:
如图2,在AF=2,DH=5的条件下,请在图2中画出周长最小的四边形EFGH,并求出周长的最小值.
探究2:
在探究1的启发下,小敏画出了图3:作F关于AD的对称点F1,作F关于BC的对称点F2,作F1关于CD的对称点F3,连接F2F3交CD于点H,交BC于点G,连接F1H交AD于点E,连接EF,FG,借助图3,他发现四边形EFGH的周长有最小值,并顺利解决了遇到的这个问题.请求出四边形EFGH的周长的最小值.
拓广探究:
解决了上述问题后,小敏又想到了新的问题,当四边形EFGH的周长最小时,四边形EFGH的面积是否存在最大值?请帮助小敏解决这个问题,若存在,请求出此时面积的最大值;若不存在,请说明理由.
解:探究1:
如答图1,作F关于AD的对称点F′,F关于BC的对称点F″,连接HF′交AD于E,连接HF″交BC于G,连接EF,FG,作HM⊥AB于M.
此时四边形EFGH的周长最小,最小值为EF+EH+GF+GH=EF′+EH+HG+GF″=HF′+HF″,
在Rt△HMF′中,HF′===,
在Rt△HMF″中,HF″===,
∴四边形EFGH的周长的最小值为+.
探究2:
由题意可知四边形EFGH的周长的最小值为HF1+HF2,
答图
易知HF1是Rt△F1F2F3的斜边的中线,
∴HF1=HF2=HF3.
在Rt△F1F2F3中,F1F2=12,F1F3=16,
∴F2F3==20,
∴四边形EFGH的周长的最小值为20.
拓广探究:
存在.理由如下:
如答图2,当四边形EFGH的周长最小时,
由探究2知HF1=HF2=HF3,∴∠F2=∠2,
由对称知∠3=∠F2,∴∠2=∠3,
∴FG∥EH.
同理可得EF∥HG,
∴四边形EFGH是平行四边形,
易知CH∶CG∶GH=3∶4∶5,
设HC=3x,GC=4x,GH=5x,
则DH=6-3x,BG=8-4x,DE=(6-3x),AE=8-(6-3x),BF=(8-4x),AF=6-(8-4x),
∴S四边形EFGH=6×8-·3x·4x-·(6-3x)·(6-3x)-·[8-(6-3x)]·[6-(8-4x)]-·(8-4x)·(8-4x)=-24x2+48x=-24(x-1)2+24.
∵-24<0,
∴当x=1时,四边形EFGH的面积最大,最大值为24.
同课章节目录
