人教版七年级数学 下册 7.2.2 用坐标表示平移 课件(共31张PPT)
文档属性
| 名称 | 人教版七年级数学 下册 7.2.2 用坐标表示平移 课件(共31张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 730.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-02-12 00:00:00 | ||
图片预览









文档简介
(共31张PPT)
名言欣赏:
数学是打开科学大门的钥匙。
——培根
1、利用平面直角坐标系表示地理位置:
(1)建立坐标系,选择一个适当的参照点为原点、确定x轴、 y轴的正方向;
(2)根据具体问题确定适当的比例尺,在坐标轴上标出单位长度;
(3)在坐标平面内画出这些点、写出各点的坐标和各个地点的名称.
知识回顾
2. 什么叫做平移?
3 .平移后得到的新图形与原图形有什么关系?
把一个图形整体沿某一方向移动一定的距离,图形的这种移动,叫做平移。
平移后图形只改变位置,形状、大小不变。
4.连结各组对应点的线段
平行且相等。
知识回顾
7.2.2 用坐标表示平移
人教版七年级数学 下册
目标导航
1.掌握平面直角坐标系中的点或图形平移引起的点的坐标的变化规律;(重点、难点)
2.体会平面直角坐标系是数与形之间的桥梁,感受代数与几何的相互转化,初步建立空间概念。
认真阅读课本中7.2.2 用坐标表示平移的内容,完成下面练习并体验知识点的形成过程。
自主研学
A
1
3
5
2
4
6
-1
-2
-3
-4
-5
-6
O
3
4
2
-1
5
-2
-3
-4
-6
-5
6
1
根据左图回答问题:
1.将点A(-2,-3)向右平移5个单位长度,得到点A1( ___ , ___ );
2.将点A(-2,-3)向左平移
2个单位长度,得到点A2(____ , _____);
A1
-4
-3
3
-3
A2
y
x
合作探究
A
1
3
5
2
4
6
-1
-2
-3
-4
-5
-6
3
4
2
-1
5
-2
-3
-4
-6
-5
6
O
1
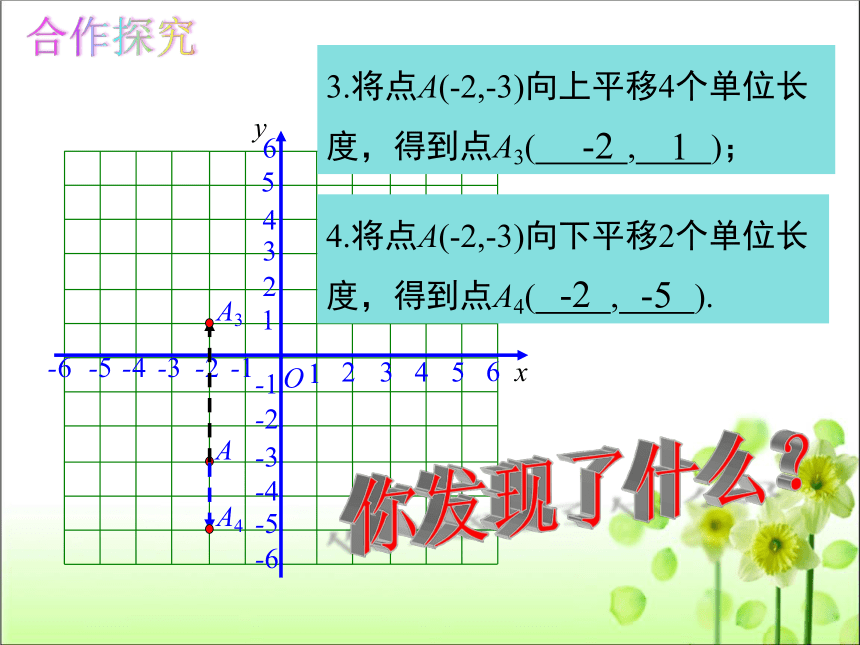
3.将点A(-2,-3)向上平移4个单位长度,得到点A3( , );
4.将点A(-2,-3)向下平移2个单位长度,得到点A4( , ).
A3
A4
-2
1
-2
-5
y
x
你发现了什么?
合作探究
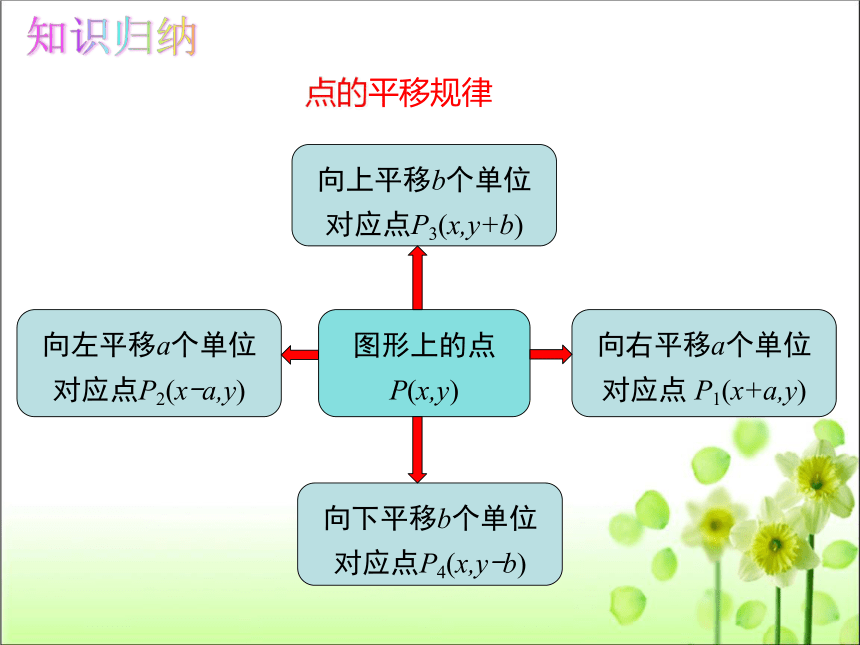
向左平移a个单位对应点P2(x-a,y)
向右平移a个单位对应点 P1(x+a,y)
向上平移b个单位对应点P3(x,y+b)
向下平移b个单位对应点P4(x,y-b)
图形上的点P(x,y)
点的平移规律
知识归纳
平移规律归纳:在平面直角坐标系中,将点(x,y)向右(或左)平移a个单位长度,可以得到对应点(x+a,y)(或(_____ ,_____ ));将点(x,y)向上(或下)平移b个单位长度,可以得到对应点(x,y+b)(或(_______ ,________)).
x-a y
x y-b
知识归纳
左右平移:左减右加纵不变
上下平移:上加下减横不变
口诀
0
1
-1
1
-1
x
y
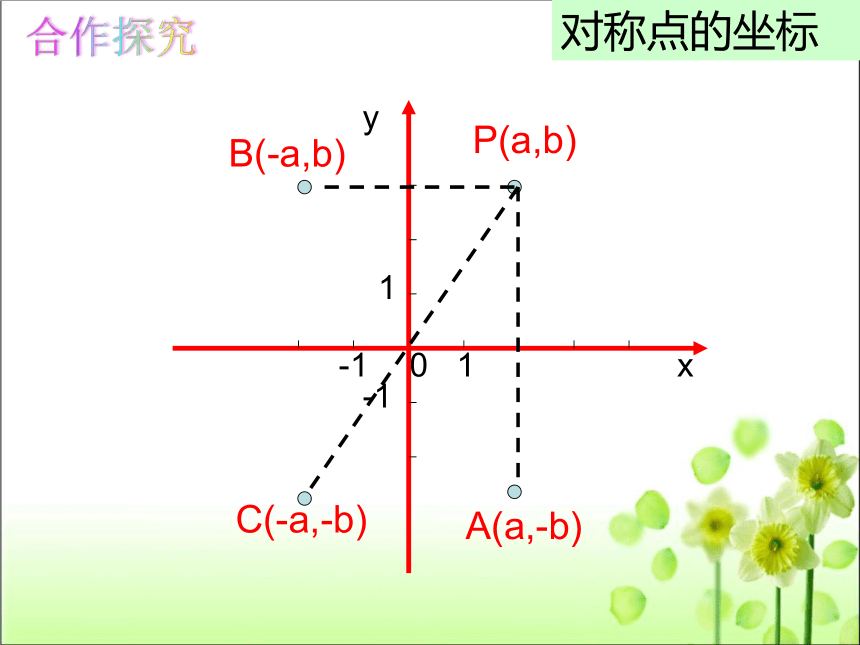
P(a,b)
A(a,-b)
B(-a,b)
C(-a,-b)
对称点的坐标
合作探究
0
1
-1
1
-1
x
y
P(a,b)
A(a,-b)
B(-a,b)
C(-a,-b)
横轴横不变
纵轴纵不变
原点对称两纵皆变
合作探究
在坐标中描出点A(-2,-3)并进行如下平移:
1、(1)将点A向右平移5个单位长度得到点A1,则 点A1的坐标是 ;
(2)将点A向左平移3个单位长度得到点A2,则 点A2的坐标是 ;
(3)将点A向右平移a(a>o)个单位长度得到点An,则 点An的坐标是 ;
(4)将点A向左平移a(a>o)个单位长度得到点An?,则 点An ?的坐标是 ;
(-2-a ,-3)
(3,-3)
( -5 ,-3)
(-2+ a ,-3)
即学即练
例 如图,三角形ABC三个顶点坐标分别是A(4,3),B(3,1),C(1,2).
-4-3 -2-1 O 1 2 3 4 x
3
2
1
-2
-1
-3
4
y
A
B
C
典型例题
例 如图,三角形ABC三个顶点坐标分别是A(4,3),B(3,1),C(1,2).
-4-3 -2-1 O 1 2 3 4 x
3
2
1
-2
-1
-3
4
y
(1)将三角形ABC三个顶点的横坐标都减去6,纵坐标不变,分别得到点A1,B1,C1,依次连接A1,B1,C1各点,所得三角形A1B1C1与三角形ABC的大小、形状和位置上有什么关系?
A
B
C
A1
B1
C1
典型例题
-4-3 -2-1 O 1 2 3 4 x
3
2
1
-2
-1
-3
4
y
A
B
C
(2)将三角形ABC三个顶点的纵坐标都减去5,横坐标不变,分别得到点A2,B2,C2,依次连接A2,B2,C2各点,所得三角形A2B2C2与三角形ABC的大小、形状和位置上有什么关系?
A2
B2
C2
例 如图,三角形ABC三个顶点坐标分别是A(4,3),B(3,1),C(1,2).
典型例题
-3 -2-1 O 1 2 3 4 5 6 7 x
3
2
1
-2
-1
-3
4
y
A
B
C
思考:
(1)如果将三角形ABC三个顶点的横坐标都加3,能得出什么结论?
例 如图,三角形ABC三个顶点坐标分别是A(4,3),B(3,1),C(1,2).
典型例题
-4-3 -2-1 O 1 2 3 4 x
3
2
1
-2
-1
-3
4
y
A
B
C
思考:
(1)如果将三角形ABC三个顶点的纵坐标都加2,能得出什么结论?
5
例 如图,三角形ABC三个顶点坐标分别是A(4,3),B(3,1),C(1,2).
典型例题
-5 -4-3 -2-1 O 1 2 3 4 x
3
2
1
-2
-1
-3
4
y
A
B
C
思考:
(2)如果将三角形ABC三个顶点的横坐标都减去6,同时纵坐标都减去5,能得出什么结论?
-4
例 如图,三角形ABC三个顶点坐标分别是A(4,3),B(3,1),C(1,2).
典型例题
将△ABC三个顶点的横坐标都减 6,纵坐标减5,又能得到什么结论?
①
②
总结:图形的斜向平移,
可通过左右平移和上下平移来完成。
2
1
-1
-2
-3
-4
-6
-4
-2
2
4
x
y
1
2
3
4
-
2
1
2
-
1
-
5
-
3
-
1
-
2
0
-
3
-
4
-
4
A
C
B
A
C
B
A
C
B
A
1
C
1
B
1
A
1
C
1
B
1
A
1
C
1
B
1
A
1
C
1
B
1
A
1
C
1
B
1
A
1
C
1
B
1
1
2
3
合作探究
5
4
3
2
1
-2 -1 0 1 2 3 4 5 6
-1
-2
如图,将平行四边形ABCD向左平移2个单位长度,可以得到平行四边形A1B2C3D4,画出平移后得图形,并指出各个顶点得坐标。
A1
B1
C1
D1
A
B
C
D
即学即练
一个图形依次沿x轴方向、y轴方向平移后所得图形与原来的图形相比,位置有什么变化?它们对应点的坐标之间有怎样的关系?
平移方向和平移距离 对应点的坐标
向右平移a个单位长度,向上平移b个单位长度
向右平移a个单位长度,向下平移b个单位长度
向左平移a个单位长度,向上平移b个单位长度
向左平移a个单位长度,向下平移b个单位长度
(x+a , y+b)
(x+a , y-b)
(x-a , y+b)
(x-a , y-b)
课堂小结
1、已知△ABC在平面直角坐标系中的位置如图所示,将△ABC向下平移5个单位,再向左平移2个单位,则平移后C点的坐标是( )
A、(5,-2)
B、(1,-2)
C、(2,-1)
D、(2,-2)
B
A
B
C
O
x
y
检测目标
(3)点(a, b )关于原点的对称点是( )
(2)点(a, b )关于Y 轴的对称点是( b)
(1)点(a, b )关于X轴的对称点是( )
a, -b
- a,
-a, -b
检测目标
2、关于对称点
3.点A`(6,3)是由点A(-2,3)经过____
______________得到的.点B(4,3)向______________得到B`(6,3)
向右平
移8个单位长度
右平移2个单位长度
检测目标
4、如图△ABC中任意一点P(x,y)经平移后对应点为P1(x+5,y+3),将△ABC作同样的平移到△A1B1C1。求A1、B1、C1的坐标
(2)
(2)
A1(3,6)
B1(1,4)
C1(7,3)
A(-2,3)
B(-4,-1)
C(2,0)
检测目标
我们已经站在了人生的起跑线上,为了实现心中的远大目标,我们正努力拼搏着。成功属于不畏困难、勇往直前的人。相信自己!
教师寄语
通过本课学习,你收获了什么?
课后作业:
完成教科书中相关练习题。
名言欣赏:
数学是打开科学大门的钥匙。
——培根
1、利用平面直角坐标系表示地理位置:
(1)建立坐标系,选择一个适当的参照点为原点、确定x轴、 y轴的正方向;
(2)根据具体问题确定适当的比例尺,在坐标轴上标出单位长度;
(3)在坐标平面内画出这些点、写出各点的坐标和各个地点的名称.
知识回顾
2. 什么叫做平移?
3 .平移后得到的新图形与原图形有什么关系?
把一个图形整体沿某一方向移动一定的距离,图形的这种移动,叫做平移。
平移后图形只改变位置,形状、大小不变。
4.连结各组对应点的线段
平行且相等。
知识回顾
7.2.2 用坐标表示平移
人教版七年级数学 下册
目标导航
1.掌握平面直角坐标系中的点或图形平移引起的点的坐标的变化规律;(重点、难点)
2.体会平面直角坐标系是数与形之间的桥梁,感受代数与几何的相互转化,初步建立空间概念。
认真阅读课本中7.2.2 用坐标表示平移的内容,完成下面练习并体验知识点的形成过程。
自主研学
A
1
3
5
2
4
6
-1
-2
-3
-4
-5
-6
O
3
4
2
-1
5
-2
-3
-4
-6
-5
6
1
根据左图回答问题:
1.将点A(-2,-3)向右平移5个单位长度,得到点A1( ___ , ___ );
2.将点A(-2,-3)向左平移
2个单位长度,得到点A2(____ , _____);
A1
-4
-3
3
-3
A2
y
x
合作探究
A
1
3
5
2
4
6
-1
-2
-3
-4
-5
-6
3
4
2
-1
5
-2
-3
-4
-6
-5
6
O
1
3.将点A(-2,-3)向上平移4个单位长度,得到点A3( , );
4.将点A(-2,-3)向下平移2个单位长度,得到点A4( , ).
A3
A4
-2
1
-2
-5
y
x
你发现了什么?
合作探究
向左平移a个单位对应点P2(x-a,y)
向右平移a个单位对应点 P1(x+a,y)
向上平移b个单位对应点P3(x,y+b)
向下平移b个单位对应点P4(x,y-b)
图形上的点P(x,y)
点的平移规律
知识归纳
平移规律归纳:在平面直角坐标系中,将点(x,y)向右(或左)平移a个单位长度,可以得到对应点(x+a,y)(或(_____ ,_____ ));将点(x,y)向上(或下)平移b个单位长度,可以得到对应点(x,y+b)(或(_______ ,________)).
x-a y
x y-b
知识归纳
左右平移:左减右加纵不变
上下平移:上加下减横不变
口诀
0
1
-1
1
-1
x
y
P(a,b)
A(a,-b)
B(-a,b)
C(-a,-b)
对称点的坐标
合作探究
0
1
-1
1
-1
x
y
P(a,b)
A(a,-b)
B(-a,b)
C(-a,-b)
横轴横不变
纵轴纵不变
原点对称两纵皆变
合作探究
在坐标中描出点A(-2,-3)并进行如下平移:
1、(1)将点A向右平移5个单位长度得到点A1,则 点A1的坐标是 ;
(2)将点A向左平移3个单位长度得到点A2,则 点A2的坐标是 ;
(3)将点A向右平移a(a>o)个单位长度得到点An,则 点An的坐标是 ;
(4)将点A向左平移a(a>o)个单位长度得到点An?,则 点An ?的坐标是 ;
(-2-a ,-3)
(3,-3)
( -5 ,-3)
(-2+ a ,-3)
即学即练
例 如图,三角形ABC三个顶点坐标分别是A(4,3),B(3,1),C(1,2).
-4-3 -2-1 O 1 2 3 4 x
3
2
1
-2
-1
-3
4
y
A
B
C
典型例题
例 如图,三角形ABC三个顶点坐标分别是A(4,3),B(3,1),C(1,2).
-4-3 -2-1 O 1 2 3 4 x
3
2
1
-2
-1
-3
4
y
(1)将三角形ABC三个顶点的横坐标都减去6,纵坐标不变,分别得到点A1,B1,C1,依次连接A1,B1,C1各点,所得三角形A1B1C1与三角形ABC的大小、形状和位置上有什么关系?
A
B
C
A1
B1
C1
典型例题
-4-3 -2-1 O 1 2 3 4 x
3
2
1
-2
-1
-3
4
y
A
B
C
(2)将三角形ABC三个顶点的纵坐标都减去5,横坐标不变,分别得到点A2,B2,C2,依次连接A2,B2,C2各点,所得三角形A2B2C2与三角形ABC的大小、形状和位置上有什么关系?
A2
B2
C2
例 如图,三角形ABC三个顶点坐标分别是A(4,3),B(3,1),C(1,2).
典型例题
-3 -2-1 O 1 2 3 4 5 6 7 x
3
2
1
-2
-1
-3
4
y
A
B
C
思考:
(1)如果将三角形ABC三个顶点的横坐标都加3,能得出什么结论?
例 如图,三角形ABC三个顶点坐标分别是A(4,3),B(3,1),C(1,2).
典型例题
-4-3 -2-1 O 1 2 3 4 x
3
2
1
-2
-1
-3
4
y
A
B
C
思考:
(1)如果将三角形ABC三个顶点的纵坐标都加2,能得出什么结论?
5
例 如图,三角形ABC三个顶点坐标分别是A(4,3),B(3,1),C(1,2).
典型例题
-5 -4-3 -2-1 O 1 2 3 4 x
3
2
1
-2
-1
-3
4
y
A
B
C
思考:
(2)如果将三角形ABC三个顶点的横坐标都减去6,同时纵坐标都减去5,能得出什么结论?
-4
例 如图,三角形ABC三个顶点坐标分别是A(4,3),B(3,1),C(1,2).
典型例题
将△ABC三个顶点的横坐标都减 6,纵坐标减5,又能得到什么结论?
①
②
总结:图形的斜向平移,
可通过左右平移和上下平移来完成。
2
1
-1
-2
-3
-4
-6
-4
-2
2
4
x
y
1
2
3
4
-
2
1
2
-
1
-
5
-
3
-
1
-
2
0
-
3
-
4
-
4
A
C
B
A
C
B
A
C
B
A
1
C
1
B
1
A
1
C
1
B
1
A
1
C
1
B
1
A
1
C
1
B
1
A
1
C
1
B
1
A
1
C
1
B
1
1
2
3
合作探究
5
4
3
2
1
-2 -1 0 1 2 3 4 5 6
-1
-2
如图,将平行四边形ABCD向左平移2个单位长度,可以得到平行四边形A1B2C3D4,画出平移后得图形,并指出各个顶点得坐标。
A1
B1
C1
D1
A
B
C
D
即学即练
一个图形依次沿x轴方向、y轴方向平移后所得图形与原来的图形相比,位置有什么变化?它们对应点的坐标之间有怎样的关系?
平移方向和平移距离 对应点的坐标
向右平移a个单位长度,向上平移b个单位长度
向右平移a个单位长度,向下平移b个单位长度
向左平移a个单位长度,向上平移b个单位长度
向左平移a个单位长度,向下平移b个单位长度
(x+a , y+b)
(x+a , y-b)
(x-a , y+b)
(x-a , y-b)
课堂小结
1、已知△ABC在平面直角坐标系中的位置如图所示,将△ABC向下平移5个单位,再向左平移2个单位,则平移后C点的坐标是( )
A、(5,-2)
B、(1,-2)
C、(2,-1)
D、(2,-2)
B
A
B
C
O
x
y
检测目标
(3)点(a, b )关于原点的对称点是( )
(2)点(a, b )关于Y 轴的对称点是( b)
(1)点(a, b )关于X轴的对称点是( )
a, -b
- a,
-a, -b
检测目标
2、关于对称点
3.点A`(6,3)是由点A(-2,3)经过____
______________得到的.点B(4,3)向______________得到B`(6,3)
向右平
移8个单位长度
右平移2个单位长度
检测目标
4、如图△ABC中任意一点P(x,y)经平移后对应点为P1(x+5,y+3),将△ABC作同样的平移到△A1B1C1。求A1、B1、C1的坐标
(2)
(2)
A1(3,6)
B1(1,4)
C1(7,3)
A(-2,3)
B(-4,-1)
C(2,0)
检测目标
我们已经站在了人生的起跑线上,为了实现心中的远大目标,我们正努力拼搏着。成功属于不畏困难、勇往直前的人。相信自己!
教师寄语
通过本课学习,你收获了什么?
课后作业:
完成教科书中相关练习题。
