北师大版九年级数学下册 第3章 圆 同步单元练习 (含答案解析)
文档属性
| 名称 | 北师大版九年级数学下册 第3章 圆 同步单元练习 (含答案解析) |  | |
| 格式 | zip | ||
| 文件大小 | 910.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-02-13 09:19:44 | ||
图片预览




文档简介
北师大版九年级数学下册第3章 圆 同步单元练习
一.选择题(共20小题)
1.如图,AB是⊙O的直径,AB=10,P是半径OA上的一动点,PC⊥AB交⊙O于点C,在半径OB上取点Q,使得OQ=CP,DQ⊥AB交⊙O于点D,点C,D位于AB两侧,连接CD交AB于点F,点P从点A出发沿AO向终点O运动,在整个运动过程中,△CFP与△DFQ的面积和的变化情况是( )
A.一直减小 B.一直不变
C.先变大后变小 D.先变小后变大
2.如图中正方形、矩形、圆的面积相等,则周长L的大小关系是( )
A.LA>LB>LC B.LA<LB<LC C.LB>LC>LA D.LC<LA<LB
3.某品牌婴儿罐装奶粉圆形桶口如图所示,它的内直径(⊙O直径)为10cm,弧AB的度数约为90°,则弓形铁片ACB(阴影部分) 的面积约为( )
A.(π﹣)cm2 B.(π﹣25)cm2
C.(π﹣)cm2 D.(25π﹣)cm2
4.已知AB、CD是两个不同圆的弦,如AB=CD,那么与的关系是( )
A. B. C. D.不能确定
5.如图,AB是⊙O的直径,点C、D在圆上,若∠D=45°,则tan∠ABC等于( )
A. B. C.1 D.
6.如图所示,四边形ABCD为⊙O的内接四边形,∠BCD=120°,则∠BOD的大小是( )
A.80° B.120° C.100° D.90°
7.如图,AB为⊙O的直径,AB=10cm,弦CD⊥AB,垂足为E,且AE:EB=2:3,则AC=( )
A.3cm B.4cm C.cm D.cm
8.一个点到圆的最小距离为4cm,最大距离为9cm,则该圆的半径是( )
A.2.5cm或6.5cm B.2.5cm
C.6.5cm D.5cm或13cm
9.考虑下面六个命题(1)任意三点确定一个圆;(2)平分弦的直径垂直于弦,且平分这条弦所对的弧;(3)90°的圆周角所对的弦是直径;(4)同弧或等弧所对的圆周角相等;(5)相等的圆周角所对的弧相等.其中正确的命题有( )
A.2个 B.3个 C.4个 D.5个
10.已知:点A(0,4),B(0,﹣6),C为x轴正半轴上一点,且满足∠ACB=45°,则( )
A.△ABC外接圆的圆心在OC上
B.∠BAC=60°
C.△ABC外接圆的半径等于5
D.OC=12
11.已知圆O的半径为3cm,点P是直线l上的一点,且OP=3cm,则直线l与圆O的位置关系为( )
A.相切 B.相交 C.相离 D.不能确定
12.如图,点O′在第一象限,⊙O′与x轴相切于H点,与y轴相交于A(0,2),B(0,8),则点O′的坐标是( )
A.(6,4) B.(4,6) C.(5,4) D.(4,5)
13.如下图,已知⊙O的直径为AB,AC⊥AB于点A,BC与⊙O相交于点D,在AC上取一点E,使得ED=EA.下面四个结论:
①ED是⊙O的切线;②BC=2OE;③△BOD为等边三角形;④△EOD∽△CAD
正确的是( )
A.①② B.②④ C.①②④ D.①②③④
14.如图,直线l1∥l2,⊙O与l1和l2分别相切于点A和点B.点M和点N分别是l1和l2上的动点,MN沿l1和l2平移.⊙O的半径为1,∠1=60°.下列结论错误的是( )
A.
B.l1和l2的距离为2
C.若∠MON=90°,则MN与⊙O相切
D.若MN与⊙O相切,则
15.如图,PA、PB、DE分别与⊙O相切,若∠P=40°,则∠DOE等于( )度.
A.40 B.50 C.70 D.80
16.如图,⊙O是四边形ABCD的内切圆,下列结论一定正确的有( )个:
①AF=BG;②CG=CH;③AB+CD=AD+BC;④BG<CG.
A.1 B.2 C.3 D.4
17.如图,PAB为⊙O的割线,且PA=AB=3,PO交⊙O于点C,若PC=2,则⊙O的半径的长为( )
A. B. C. D.7
18.如图,点I是△ABC的内心,若∠AIB=125°,则∠C等于( )
A.65° B.70° C.75° D.80°
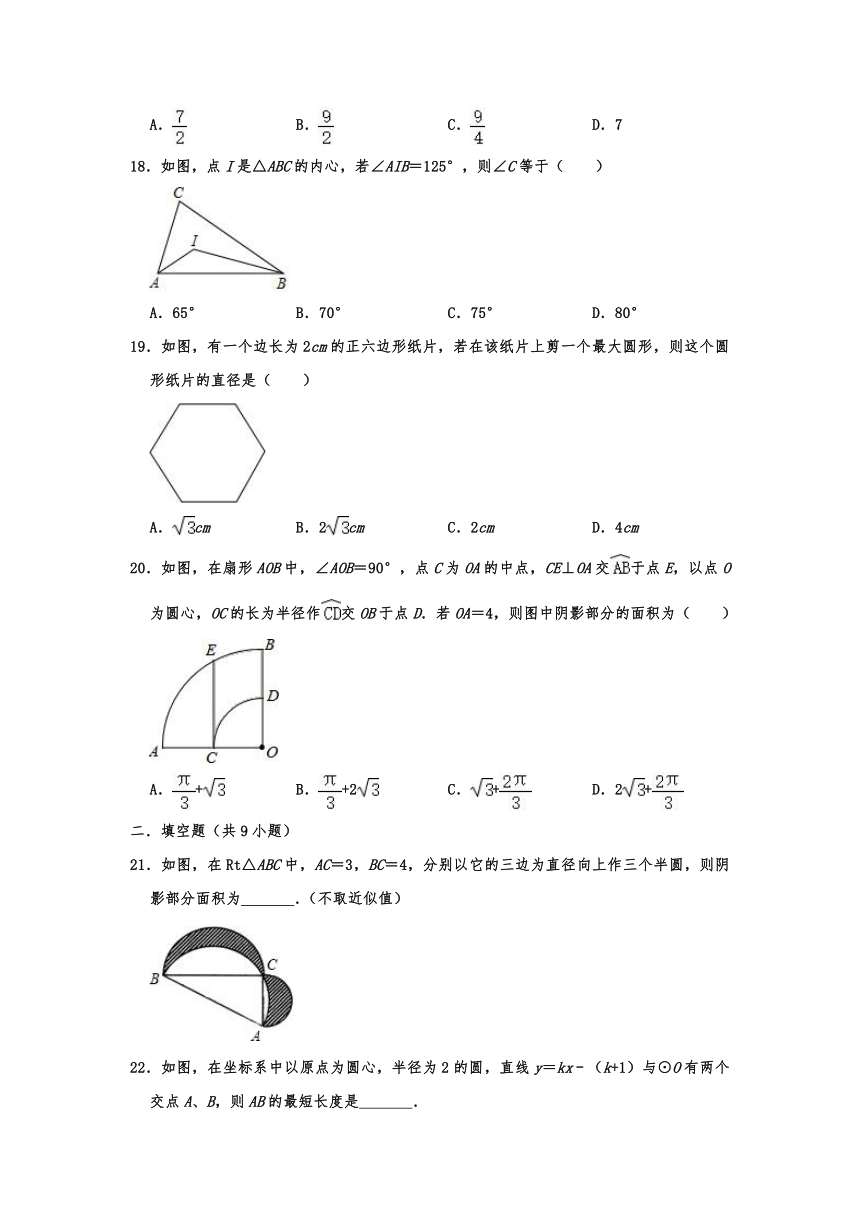
19.如图,有一个边长为2cm的正六边形纸片,若在该纸片上剪一个最大圆形,则这个圆形纸片的直径是( )
A.cm B.2cm C.2cm D.4cm
20.如图,在扇形AOB中,∠AOB=90°,点C为OA的中点,CE⊥OA交于点E,以点O为圆心,OC的长为半径作交OB于点D.若OA=4,则图中阴影部分的面积为( )
A.+ B.+2 C.+ D.2+
二.填空题(共9小题)
21.如图,在Rt△ABC中,AC=3,BC=4,分别以它的三边为直径向上作三个半圆,则阴影部分面积为 .(不取近似值)
22.如图,在坐标系中以原点为圆心,半径为2的圆,直线y=kx﹣(k+1)与⊙O有两个交点A、B,则AB的最短长度是 .
23.为改善市区人居环境,某市建设污水管网工程,已知圆柱形污水管的直径为50cm,截面如图所示,当管内污水的面宽AB=40cm时,污水的最大深度为 cm.
24.如图,⊙O是△ABC的外接圆,已知∠ABO=40°,则∠ACB的大小为 .
25.如图,四边形ABCD内接于⊙O,AB为⊙O的直径,点D为的中点,若∠B=50°,则∠A的度数为 度.
26.如图,在⊙O中,弦AB平分弦CD于E,若CD=8,AE:EB=1:4,则弦AB= .
27.已知点P在半径为5的⊙O外,如果设OP=x,那么x的取值范围是 .
28.若A(1,2),B(3,﹣3),C(x,y)三点可以确定一个圆,则x、y需要满足的条件是 .
29.△ABC的三边分别是3,4,5,则△ABC的外接圆的半径是 .
三.解答题(共11小题)
30.已知;如图,在⊙O中,C、D分别是半径OA、BO的中点,求证:AD=BC.
31.如图,⊙O中,直径CD⊥弦AB于E,AM⊥BC于M,交CD于N,连接AD.
(1)求证:AD=AN;
(2)若AB=8,ON=1,求⊙O的半径.
32.如图,一面墙上有一个矩形的门洞,现要将它改为一个圆弧形的门洞,圆弧所在的圆外接矩形,已知矩形的高AC=2米,宽CD=米.
(1)求此圆形门洞的半径;
(2)求要打掉墙体的面积.
33.如图,边长为2的正方形ABCD各边的延长线和反向延长线与⊙O的交点把⊙O分成8条相等的弧,则⊙O的半径是 .
34.如图,四边形ABCD是⊙O的内接四边形,=,AC为直径,DE⊥BC,垂足为E.
(1)求证:CD平分∠ACE;
(2)若AC=9,CE=3,求CD的长.
35.如图,以点O′(1,1)为圆心,OO′为半径画圆,判断点P(﹣1,1),点Q(1,0),点R(2,2)和⊙O′的位置关系.
36.如图,点O为Rt△ABC斜边AB上的一点,以OA为半径的⊙O与BC切于点D,与AC交于点E,连接AD.
(1)求证:AD平分∠BAC;
(2)若∠BAC=60°,OA=2,求阴影部分的面积(结果保留π).
37.如图,PA,PB分别为⊙O的切线,AC为直径,切点分别为A、B,∠P=70°,则∠C= .
38.如图,在⊙O上依次有A、B、C三点,BO的延长线交⊙O于E,,过点C作CD∥AB交BE的延长线于D,AD交⊙O于点F.
(1)求证:四边形ABCD是菱形;
(2)连接OA、OF,若∠AOF=3∠FOE且AF=3,求劣弧的长.
39.如图,AB是⊙O的直径,点D在⊙O上,∠DAB=45°,BC∥AD,CD∥AB.若⊙O的半径为1,求图中阴影部分的面积(结果保留π).
40.如图,已知⊙O半径为10cm,弦AB垂直平分半径OC,并交OC于点D.
(1)求弦AB的长;
(2)求弧AB的长,并求出图中阴影部分面积.
参考答案与试题解析
一.选择题(共20小题)
1.如图,AB是⊙O的直径,AB=10,P是半径OA上的一动点,PC⊥AB交⊙O于点C,在半径OB上取点Q,使得OQ=CP,DQ⊥AB交⊙O于点D,点C,D位于AB两侧,连接CD交AB于点F,点P从点A出发沿AO向终点O运动,在整个运动过程中,△CFP与△DFQ的面积和的变化情况是( )
A.一直减小 B.一直不变
C.先变大后变小 D.先变小后变大
【分析】连接OC,OD,PD,CQ.设PC=x,OP=y,OF=a,利用分割法求出阴影部分的面积,再求出a=y﹣x即可判断;
【解答】解:连接OC,OD,PD,CQ.设PC=x,OP=y,OF=a,
∵PC⊥AB,QD⊥AB,
∴∠CPO=∠OQD=90°,
∵PC=OQ,OC=OD,
∴Rt△OPC≌Rt△DQO,
∴OP=DQ=y,
∴S阴=S四边形PCQD﹣S△PFD﹣S△CFQ=(x+y)2﹣?(y﹣a)y﹣(x+a)x=xy+a(y﹣x),
∵PC∥DQ,
∴=,
∴=,
∴a=y﹣x,
∴S阴=xy+(y﹣x)(y﹣x)=(x2+y2)=
故选:B.
2.如图中正方形、矩形、圆的面积相等,则周长L的大小关系是( )
A.LA>LB>LC B.LA<LB<LC C.LB>LC>LA D.LC<LA<LB
【分析】设相同的面积为未知数,进而判断出相应的周长,比较即可.
【解答】解:设面积是S.
则正方形的边长是,则周长LA=4==4;
长方形的一边长x,则另一边长为,则周长LB=2(x+),
∵(x+)2≥0
∴x+≥2,
∴LB≥4,
即LB≥;
圆的半径为,LC=2π×=,
∵<,
∴LC<LA<LB.
故选:D.
3.某品牌婴儿罐装奶粉圆形桶口如图所示,它的内直径(⊙O直径)为10cm,弧AB的度数约为90°,则弓形铁片ACB(阴影部分) 的面积约为( )
A.(π﹣)cm2 B.(π﹣25)cm2
C.(π﹣)cm2 D.(25π﹣)cm2
【分析】连接OA、OB,根据已知求出OA=OB=5cm,∠BOA=90°,分别求出扇形BOA和△BOA的面积即可.
【解答】解:
连接OA、OB,
∵品牌婴儿罐装奶粉圆形桶口如图所示,它的内直径(⊙O直径)为10cm,弧AB的度数约为90°,
∴OA=OB=5cm,∠BOA=90°,
∴阴影部分的面积S=S扇形BOA﹣S△BOA=﹣=(π﹣)cm2,
故选:A.
4.已知AB、CD是两个不同圆的弦,如AB=CD,那么与的关系是( )
A. B. C. D.不能确定
【分析】根据在同圆和等圆中相等的弦所对的弧相等分析,从而得到答案.
【解答】解:在同圆和等圆中相等的弦所对的弧才会相等,要注意同圆和的条件,本题是两个不同的圆,所以无法判断两弦所对的弧的大小,故选D.
5.如图,AB是⊙O的直径,点C、D在圆上,若∠D=45°,则tan∠ABC等于( )
A. B. C.1 D.
【分析】连接AC,如图,根据圆周角定理得到∠ACB=90°,∠A=∠D=45°,则利用互余得到∠ABC=45°,然后根据特殊角的三角函数值求解.
【解答】解:连接AC,如图,
∵AB是⊙O的直径,
∴∠ACB=90°,
∵∠A=∠D=45°,
∴∠ABC=45°,
∴tan∠ABC=tan45°=1.
故选:C.
6.如图所示,四边形ABCD为⊙O的内接四边形,∠BCD=120°,则∠BOD的大小是( )
A.80° B.120° C.100° D.90°
【分析】根据圆内接四边形的性质求出∠A,再根据圆周角定理解答.
【解答】解:∵四边形ABCD为⊙O的内接四边形,
∴∠A=180°﹣∠BCD=60°,
由圆周角定理得,∠BOD=2∠A=120°,
故选:B.
7.如图,AB为⊙O的直径,AB=10cm,弦CD⊥AB,垂足为E,且AE:EB=2:3,则AC=( )
A.3cm B.4cm C.cm D.cm
【分析】由垂径定理得到CE=DE,又根据相交弦定理得到CE?ED=AE?EB,即CE2=AE?BE,可求得CE,再由勾股定理求出AC即可.
【解答】解:∵CD⊥AB,∴CE=DE,
∴CE2=AE?BE,
∵AB=10cm,且AE:EB=2:3,
∴AE=4cm,EB=6cm,
∴CE=2cm,
∴AC===2cm.
故选:D.
8.一个点到圆的最小距离为4cm,最大距离为9cm,则该圆的半径是( )
A.2.5cm或6.5cm B.2.5cm
C.6.5cm D.5cm或13cm
【分析】设此点为P点,圆为⊙O,最大距离为PB,最小距离为PA,有两种情况:①当此点在圆内;②当此点在圆外;分别求出半径值即可.
【解答】解:设此点为P点,圆为⊙O,最大距离为PB,最小距离为PA,则:
∵此点与圆心的连线所在的直线与圆的交点即为此点到圆心的最大、最小距离
∴有两种情况:
当此点在圆内时,如图所示,
半径OB=(PA+PB)÷2=6.5cm;
当此点在圆外时,如图所示,
半径OB=(PB﹣PA)÷2=2.5cm;
故圆的半径为2.5cm或6.5cm
故选:A.
9.考虑下面六个命题(1)任意三点确定一个圆;(2)平分弦的直径垂直于弦,且平分这条弦所对的弧;(3)90°的圆周角所对的弦是直径;(4)同弧或等弧所对的圆周角相等;(5)相等的圆周角所对的弧相等.其中正确的命题有( )
A.2个 B.3个 C.4个 D.5个
【分析】根据圆中的定理进行分析.
确定圆的定理:不在同一条直线上的三个点确定一个圆;
垂径定理的推论:平分弦(非直径)的直径垂直于弦,且平分这条弦所对的弧;
圆周角定理的推论:在同圆或等圆中,相等的圆周角所对的弧相等,同弧或等弧所对的圆周角相等;
90°的圆周角所对的弦是直径.
【解答】解:根据圆中的定理及其推论,知
(1)当三点共线的时候不能确定一个圆,故错误;
(2)当该弦是直径的时候,不一定能够垂直,故错误;
(3)和(4)根据圆周角定理的推论,故正确;
(5)必须在同圆或等圆中,故错误.
故选:A.
10.已知:点A(0,4),B(0,﹣6),C为x轴正半轴上一点,且满足∠ACB=45°,则( )
A.△ABC外接圆的圆心在OC上
B.∠BAC=60°
C.△ABC外接圆的半径等于5
D.OC=12
【分析】构造含有90°圆心角的⊙P,则⊙P与x轴的交点即为所求的点C.根据△PBA为等腰直角三角形,可得OF=PE=5,根据勾股定理得:CF=7,进而得出OC.
【解答】解:设线段BA的中点为E,
∵点A(0,4),B(0,﹣6),
∴AB=10,E(0,﹣1).
如图所示,过点E在第四象限作EP⊥BA,且EP=AB=5,则
易知△PBA为等腰直角三角形,∠BPA=90°,PA=PB=5;
以点P为圆心,PA(或PB)长为半径作⊙P,与y轴的正半轴交于点C,
∵∠BCA为⊙P的圆周角,
∴∠BCA=∠BPA=45°,即则点C即为所求.
过点P作PF⊥x轴于点F,则OF=PE=5,PF=OE=1,
在Rt△PFC中,PF=1,PC=5,
由勾股定理得:CF==7,
∴OC=OF+CF=5+7=12,
故选:D.
11.已知圆O的半径为3cm,点P是直线l上的一点,且OP=3cm,则直线l与圆O的位置关系为( )
A.相切 B.相交 C.相离 D.不能确定
【分析】直线和圆的位置关系与数量之间的联系:
若d<r,则直线与圆相交;若d=r,则直线于圆相切;若d>r,则直线与圆相离.
【解答】解:因为垂线段最短,所以圆心到直线的距离小于等于3.
此时和半径3的大小不确定,则直线和圆相交、相切都有可能.
故选:D.
12.如图,点O′在第一象限,⊙O′与x轴相切于H点,与y轴相交于A(0,2),B(0,8),则点O′的坐标是( )
A.(6,4) B.(4,6) C.(5,4) D.(4,5)
【分析】过O'作O'C⊥AB于点C,过O'作O'D⊥x轴于点D,由切线的性质可求得O'D的长,则可得O'B的长,由垂径定理可求得CB的长,在Rt△O'BC中,由勾股定理可求得O'C的长,从而可求得O'点坐标.
【解答】解:
如图,过O'作O'C⊥AB于点C,过O'作O'D⊥x轴于点D,连接O'B,
∵O'为圆心,
∴AC=BC,
∵A(0,2),B(0,8),
∴AB=8﹣2=6,
∴AC=BC=3,
∴OC=8﹣3=5,
∵⊙O'与x轴相切,
∴O'D=O'B=OC=5,
在Rt△O'BC中,由勾股定理可得O'C==4,
∴P点坐标为(4,5),
故选:D.
13.如下图,已知⊙O的直径为AB,AC⊥AB于点A,BC与⊙O相交于点D,在AC上取一点E,使得ED=EA.下面四个结论:
①ED是⊙O的切线;②BC=2OE;③△BOD为等边三角形;④△EOD∽△CAD
正确的是( )
A.①② B.②④ C.①②④ D.①②③④
【分析】如图,通过证明△AOE≌△DOE得到∠OAE=∠ODE=90°,易证得ED是⊙O的切线;证得OE是△ABC的中位线,证得BC=2OE,由OE∥BC,证得∠AEO=∠C,通过三角形全等证得∠DEO=∠C,∠ODE=∠OAE=90°,从而∠ODE=∠ADC=90°,从而证得△EOD∽△CAD.
【解答】证明:如图,连接OD.
∵AC⊥AB,
∴∠BAC=90°,即∠OAE=90°.
在△AOE与△DOE中,
,
∴△AOE≌△DOE(SSS),
∴∠OAE=∠ODE=90°,即OD⊥ED.
又∵OD是⊙O的半径,
∴ED是⊙O的切线;
∵AB是直径,
∴AD⊥BC,
∴∠DAE+∠C=90°,
∵AE=DE,
∴∠DAE=∠ADE,
∵∠ADE+∠EDC=90°,
∴∠EDC=∠C,
∴DE=EC,
∴AE=EC,
∵OA=OB,
∴OE∥BC,BC=2OE,
∴∠AEO=∠C,
∵△AOE≌△DOE,
∴∠DEO=∠C,∠ODE=∠OAE=90°,
∴∠ODE=ADC=90°,
∴△EOD∽△CAD.
∴正确的①②④,
故选:C.
14.如图,直线l1∥l2,⊙O与l1和l2分别相切于点A和点B.点M和点N分别是l1和l2上的动点,MN沿l1和l2平移.⊙O的半径为1,∠1=60°.下列结论错误的是( )
A.
B.l1和l2的距离为2
C.若∠MON=90°,则MN与⊙O相切
D.若MN与⊙O相切,则
【分析】首先过点N作NC⊥AM于点C,直线l1∥l2,⊙O与l1和l2分别相切于点A和点B,⊙O的半径为1,易求得MN==,l1和l2的距离为2;
若∠MON=90°,连接NO并延长交MA于点C,易证得CO=NO,继而可得即O到MN的距离等于半径,可证得MN与⊙O相切;
由题意可求得若MN与⊙O相切,则AM=或.
【解答】解:如图1,过点N作NC⊥AM于点C,
∵直线l1∥l2,⊙O与l1和l2分别相切于点A和点B,⊙O的半径为1,
∴CN=AB=2,
∵∠1=60°,
∴MN==,
故A与B正确;
如图3,
若∠MON=90°,连接NO并延长交MA于点C,则△AOC≌△BON,
故CO=NO,△MON≌△MOM′,故MN上的高为1,即O到MN的距离等于半径.
故C正确;
如图2,∵MN是切线,⊙O与l1和l2分别相切于点A和点B,
∴∠AMO=∠1=30°,
∴AM=;
∵∠AM′O=60°,
∴AM′=,
∴若MN与⊙O相切,则AM=或;
故D错误.
故选:D.
15.如图,PA、PB、DE分别与⊙O相切,若∠P=40°,则∠DOE等于( )度.
A.40 B.50 C.70 D.80
【分析】连接OA、OB、OF,由切线的性质得∠AOB=140°,再由切线长定理求得∠DOE的度数.
【解答】解:连接OA、OB、OF,
∵∠P=40°,
∴∠AOB=140°,
∵PA、PB、DE分别与⊙O相切,
∴∠AOD=∠FOD,∠BOE=∠FOE,
∴∠DOE=∠AOB=×140°=70°.
故选:C.
16.如图,⊙O是四边形ABCD的内切圆,下列结论一定正确的有( )个:
①AF=BG;②CG=CH;③AB+CD=AD+BC;④BG<CG.
A.1 B.2 C.3 D.4
【分析】根据切线长定理得到AF=AE,BF=BG,CG=CH,DH=DE,则AB+CD=AF+BF+CH+DH=AE+BG+CG+DE=AD+BC.
【解答】解:∵⊙O是四边形ABCD的内切圆,
∴AF=AE,BF=BG,CG=CH,DH=DE,
∴AB+CD=AF+BF+CH+DH=AE+BG+CG+DE=AD+BC.
①AF=BG;④BG<CG无法判断.
正确的有②③
故选:B.
17.如图,PAB为⊙O的割线,且PA=AB=3,PO交⊙O于点C,若PC=2,则⊙O的半径的长为( )
A. B. C. D.7
【分析】延长PO交圆于点D,利用割线定理求解;也可作OD⊥AB于D,根据垂径定理和勾股定理求解.
【解答】解法一:延长PO交圆于点D
利用割线定理可知PA?PB=PC?PD,求得PD=9,
所以CD=7,半径=3.5.
解法二:作OD⊥AB于D,根据垂径定理和勾股定理求解.
故选:A.
18.如图,点I是△ABC的内心,若∠AIB=125°,则∠C等于( )
A.65° B.70° C.75° D.80°
【分析】根据三角形内角和定理得到∠IAB+∠IBA=55°,根据内心的概念得到∠CAB+∠ABC=110°,根据三角形内角和定理计算即可.
【解答】解:∵∠AIB=125°,
∴∠IAB+∠IBA=55°,
∵点I是△ABC的内心,
∴∠IAB=∠CAB,∠IBA=∠ABC,
∴∠CAB+∠ABC=110°,
∴∠C=180°﹣(∠CAB+∠ABC)=70°,
故选:B.
19.如图,有一个边长为2cm的正六边形纸片,若在该纸片上剪一个最大圆形,则这个圆形纸片的直径是( )
A.cm B.2cm C.2cm D.4cm
【分析】根据题意画出图形,再根据正多边形圆心角的求法求出∠AOB的度数,最后根据等腰三角形及直角三角形的性质解答即可.
【解答】解:如图所示,正六边形的边长为2cm,OG⊥BC,
∵六边形ABCDEF是正六边形,
∴∠BOC=360°÷6=60°,
∵OB=OC,OG⊥BC,
∴∠BOG=∠COG==30°,
∵OG⊥BC,OB=OC,BC=2cm,
∴BG=BC=×2=1cm,
∴OB==2cm,
∴OG===,
∴圆形纸片的直径为2cm,
故选:B.
20.如图,在扇形AOB中,∠AOB=90°,点C为OA的中点,CE⊥OA交于点E,以点O为圆心,OC的长为半径作交OB于点D.若OA=4,则图中阴影部分的面积为( )
A.+ B.+2 C.+ D.2+
【分析】连接OE、AE,根据点C为OC的中点可得∠CEO=30°,继而可得△AEO为等边三角形,求出扇形AOE的面积,最后用扇形AOB的面积减去扇形COD的面积,再减去S空白AEC即可求出阴影部分的面积.
【解答】解:连接OE、AE,
∵点C为OA的中点,
∴EO=2OC,
∴∠CEO=30°,∠EOC=60°,
∴△AEO为等边三角形,
∴S扇形AOE==,
∴S阴影=S扇形AOB﹣S扇形COD﹣(S扇形AOE﹣S△COE)
=﹣﹣(﹣)
=4π﹣π﹣+2
=+2
故选:B.
二.填空题(共9小题)
21.如图,在Rt△ABC中,AC=3,BC=4,分别以它的三边为直径向上作三个半圆,则阴影部分面积为 6 .(不取近似值)
【分析】阴影部分的面积等于中间直角三角形的面积加上两个小半圆的面积,减去其中下面面积较大的半圆的面积.
【解答】解:以BC为直径的半圆的面积是2π,以AC为直径的半圆的面积是π()2=,以AB为直径的面积是×π()2=,△ABC的面积是6,因而阴影部分的面积是2π++6﹣=6.
22.如图,在坐标系中以原点为圆心,半径为2的圆,直线y=kx﹣(k+1)与⊙O有两个交点A、B,则AB的最短长度是 2 .
【分析】易知直线y=kx﹣3k+4过定点D(1,﹣1),运用勾股定理可求出OD,由于过圆内定点D的所有弦中,与OD垂直的弦最短,因此只需运用垂径定理及勾股定理就可解决问题
【解答】解:∵直线y=kx﹣(k+1)可化为y=(x﹣1)k﹣1,
∴此直线恒过点(1,﹣1).
过点D作DH⊥x轴于点H,
∵OH=1,DH=1,OD===.
∵OB=2,
∴BD===,
∴AB=2.
故答案为:2.
23.为改善市区人居环境,某市建设污水管网工程,已知圆柱形污水管的直径为50cm,截面如图所示,当管内污水的面宽AB=40cm时,污水的最大深度为 10 cm.
【分析】根据垂径定理和勾股定理求解.
【解答】解:如图1,作弦的弦心距,连接一条半径,
根据垂径定理,得半弦是20cm,
根据勾股定理,得弦心距是15cm,
则污水的最大深度是25﹣15=10cm;
故答案为10.
24.如图,⊙O是△ABC的外接圆,已知∠ABO=40°,则∠ACB的大小为 130° .
【分析】根据等腰三角形的性质、三角形内角和定理求出∠AOB,根据圆周角定理计算即可.
【解答】解:∵OA=OB,∠ABO=40°,
∴∠AOB=100°,
∴∠ACB=×(360°﹣100°)=130°,
故答案为:130°.
25.如图,四边形ABCD内接于⊙O,AB为⊙O的直径,点D为的中点,若∠B=50°,则∠A的度数为 65 度.
【分析】连接OD、OC,根据圆周角定理求出∠AOC=100°,根据三角形内角和定理计算即可.
【解答】解:连接OD、OC,
∵点D为的中点,
∴∠AOD=∠COD,
∵∠B=50°,
∴∠AOC=100°,
∴∠AOD=∠COD=50°,
∴∠A=∠ODA=65°,
故答案为:65.
26.如图,在⊙O中,弦AB平分弦CD于E,若CD=8,AE:EB=1:4,则弦AB= 10 .
【分析】设AE=x,则EB=4x,由弦AB平分弦CD于E,得到CE=DE=CD=4,再根据相交弦定理得x?4x=4?4,解得x=2或x=﹣2(舍去),然后计算5x即可.
【解答】解:设AE=x,则EB=4x,
∵弦AB平分弦CD于E,
∴CE=DE=CD=×8=4,
∵AE?BE=CE?DE,
即x?4x=4?4,解得x=2或x=﹣2(舍去),
∴AB=AE+BE=5x=10.
故答案为10.
27.已知点P在半径为5的⊙O外,如果设OP=x,那么x的取值范围是 x>5 .
【分析】根据点在圆外的判断方法得到x的取值范围.
【解答】解:∵点P在半径为5的⊙O外,
∴OP>5,即x>5.
故答案为x>5.
28.若A(1,2),B(3,﹣3),C(x,y)三点可以确定一个圆,则x、y需要满足的条件是 5x+2y≠9 .
【分析】能确定一个圆就是不在同一直线上,首先确定直线AB的解析式,然后点C不满足求得的直线即可;
【解答】解:设直线AB的解析式为y=kx+b,
∵A(1,2),B(3,﹣3),
∴,
解得:k=﹣,b=,
∴直线AB的解析式为y=﹣x+,
∵点A(1,2),B(3,﹣3),C(x,y)三点可以确定一个圆时,
∴点C不在直线AB上,
∴5x+2y≠9,
故答案为:5x+2y≠9.
29.△ABC的三边分别是3,4,5,则△ABC的外接圆的半径是 .
【分析】根据勾股定理逆定理得到△ABC是直角三角形,根据圆周角定理解答.
【解答】解:∵32+42=25,52=25,
∴32+42=52,
∴△ABC是直角三角形,
∴△ABC的外接圆的半径为,
故答案为:.
三.解答题(共11小题)
30.已知;如图,在⊙O中,C、D分别是半径OA、BO的中点,求证:AD=BC.
【分析】首先证明OC=OD,再证明△OCB≌△ODA,进而得到AD=BC.
【解答】解:∵OA、OB是⊙O的两条半径,
∴AO=BO,
∵C、D分别是半径OA、BO的中点,
∴OC=OD,
在△OCB和△ODA中,
,
∴△OCB≌△ODA(SAS),
∴AD=BC.
31.如图,⊙O中,直径CD⊥弦AB于E,AM⊥BC于M,交CD于N,连接AD.
(1)求证:AD=AN;
(2)若AB=8,ON=1,求⊙O的半径.
【分析】(1)先根据圆周角定理得出∠BAD=∠BCD,再由直角三角形的性质得出∠ANE=∠CNM,故可得出∠BCD=∠BAM,由全等三角形的判定定理得出△ANE≌△ADE,故可得出结论;
(2)先根据垂径定理求出AE的长,设NE=x,则OE=x﹣1,NE=ED=x,r=OD=OE+ED=2x﹣1连结AO,则AO=OD=2x﹣1,在Rt△AOE中根据勾股定理可得出x的值,进而得出结论.
【解答】(1)证明:∵CD⊥AB
∴∠CEB=90°
∴∠C+∠B=90°,
同理∠C+∠CNM=90°
∴∠CNM=∠B
∵∠CNM=∠AND
∴∠AND=∠B,
∵,
∴∠D=∠B,
∴∠AND=∠D,
∴AN=AD;
(2)解:设OE的长为x,连接OA
∵AN=AD,CD⊥AB
∴DE=NE=x+1,
∴OD=OE+ED=x+x+1=2x+1,
∴OA=OD=2x+1,
∴在Rt△OAE中OE2+AE2=OA2,
∴x2+42=(2x+1)2.
解得x=或x=﹣3(不合题意,舍去),
∴OA=2x+1=2×+1=,
即⊙O的半径为.
32.如图,一面墙上有一个矩形的门洞,现要将它改为一个圆弧形的门洞,圆弧所在的圆外接矩形,已知矩形的高AC=2米,宽CD=米.
(1)求此圆形门洞的半径;
(2)求要打掉墙体的面积.
【分析】(1)先证得BC是直径,在直角三角形BCD中,由BD与CD的长,利用勾股定理求出BC的长,即可求得半径;
(2)打掉墙体的面积=2(S扇形OAC﹣S△AOC)+S扇形OAB﹣S△AOB,根据扇形的面积和三角形的面积求出即可.
【解答】解:(1)连结AD、BC,
∵∠BDC=90°,
∴BC是直径,
∴BC==
∴圆形门洞的半径为.
(2)取圆心O,连结OA.由上题可知,OA=OB=AB=,
∴△AOB是正三角形,
∴∠AOB=60°,∠AOC=120°,
∴S△AOB=,S△AOC=
∴S=2(S扇形OAC﹣S△AOC)+S扇形OAB﹣S△AOB
=2(﹣)+(﹣)
=π﹣
∴打掉墙体面积为π﹣平方米.
33.如图,边长为2的正方形ABCD各边的延长线和反向延长线与⊙O的交点把⊙O分成8条相等的弧,则⊙O的半径是 .
【分析】连接MN,EW,MW,QM,证四边形QMNW和BWNC是矩形,推出WN=QM=EW=2,根据勾股定理求出BE=BW=,在Rt△MQW中根据勾股定理求出半径即可.
【解答】解:连接MN,EW,MW,QM,
∵弧QM=弧WN,
∴QM∥WN,QM=WN,∠WNM=×360°×4×=90°,
∴四边形QMNW是矩形,
∴O在MW上,
∵正方形ABCD,
∴∠WBC=∠BCN=90°,
∴四边形BCNW是矩形,
∴WN=QM=EW=2,
∵∠BEW=∠EWB=45°,
∴由勾股定理得:EB=BW=,
同理AQ=,
设圆O的半径是r,
在Rt△MQW中,由勾股定理得:MQ2+QW2=MW2,
∴22+=(2r)2
r=,
故答案为:.
34.如图,四边形ABCD是⊙O的内接四边形,=,AC为直径,DE⊥BC,垂足为E.
(1)求证:CD平分∠ACE;
(2)若AC=9,CE=3,求CD的长.
【分析】(1)根据圆内接四边形的性质得到∠DCE=∠BAD,根据圆周角定理得到∠ACD=∠BAD,证明即可;
(2)证明△DCE∽△ACD,根据相似三角形的性质列出比例式,计算即可.
【解答】(1)证明:∵四边形ABCD是⊙O内接四边形,
∴∠BAD+∠BCD=180°,
∵∠BCD+∠DCE=180°,
∴∠DCE=∠BAD,
∵=,
∴∠BAD=∠ACD,
∴∠DCE=∠ACD,
∴CD平分∠ACE;
(2)解:∵AC为直径,
∴∠ADC=90°,
∵DE⊥BC,
∴∠DEC=90°,
∴∠DEC=∠ADC,
∵∠DCE=∠ACD,
∴△DCE∽△ACD,
∴=,即=,
∴CD=3.
35.如图,以点O′(1,1)为圆心,OO′为半径画圆,判断点P(﹣1,1),点Q(1,0),点R(2,2)和⊙O′的位置关系.
【分析】点与圆的位置关系由三种:设点到圆心的距离为d,则当d=r时,点在圆上;当d>r时,点在圆外;当d<r时,点在圆内.
【解答】解:∵OO′=r==,O′P==2
同理可得:O′Q=1,O′R=,
∴O′P>r,点P在⊙O′外;
O′Q<r,点Q在⊙O′内;
O′R=r,点R在⊙O′上.
36.如图,点O为Rt△ABC斜边AB上的一点,以OA为半径的⊙O与BC切于点D,与AC交于点E,连接AD.
(1)求证:AD平分∠BAC;
(2)若∠BAC=60°,OA=2,求阴影部分的面积(结果保留π).
【分析】(1)由Rt△ABC中,∠C=90°,⊙O切BC于D,易证得AC∥OD,继而证得AD平分∠CAB.
(2)如图,连接ED,根据(1)中AC∥OD和菱形的判定与性质得到四边形AEDO是菱形,则△AEM≌△DMO,则图中阴影部分的面积=扇形EOD的面积.
【解答】(1)证明:∵⊙O切BC于D,
∴OD⊥BC,
∵AC⊥BC,
∴AC∥OD,
∴∠CAD=∠ADO,
∵OA=OD,
∴∠OAD=∠ADO,
∴∠OAD=∠CAD,
即AD平分∠CAB;
(2)设EO与AD交于点M,连接ED.
∵∠BAC=60°,OA=OE,
∴△AEO是等边三角形,
∴AE=OA,∠AOE=60°,
∴AE=AO=OD,
又由(1)知,AC∥OD即AE∥OD,
∴四边形AEDO是菱形,则△AEM≌△DMO,∠EOD=60°,
∴S△AEM=S△DMO,
∴S阴影=S扇形EOD==π.
37.如图,PA,PB分别为⊙O的切线,AC为直径,切点分别为A、B,∠P=70°,则∠C= 55° .
【分析】由切线长定理,得△PAB为等腰三角形,可求得∠PAB的度数,再由切线的性质求出∠OAB,再由直径所对的圆周角等于90°和三角形的内角和定理,求得∠C即可.
【解答】解:∵PA,PB分别为⊙O的切线,∴PA=PB,
∵∠P=70°,∴∠PAB=(180°﹣70°)=55°,
∴∠OAB=90°﹣55°=35°,
∵AC为直径,∴∠ABC=90°,
∴∠C=180°﹣90°﹣35°
=55°,
故答案为55°.
38.如图,在⊙O上依次有A、B、C三点,BO的延长线交⊙O于E,,过点C作CD∥AB交BE的延长线于D,AD交⊙O于点F.
(1)求证:四边形ABCD是菱形;
(2)连接OA、OF,若∠AOF=3∠FOE且AF=3,求劣弧的长.
【分析】(1)先根据圆的性质得:∠CBD=∠ABD,由平行线的性质得:∠ABD=∠CDB,根据直径和等式的性质得:,由一组对边平行且相等可得四边形ABCD是平行四边形,由AB=BC可得结论;
(2)先设∠FOE=x,则∠AOF=3x,根据∠ABC+∠BAD=180°,列方程得:4x+2x+(180﹣3x)=180,求出x的值,接着求所对的圆心角和半径的长,根据弧长公式可得结论.
【解答】(1)证明:∵,
∴∠CBD=∠ABD,
∵CD∥AB,
∴∠ABD=∠CDB,
∴∠CBD=∠CDB,
∴CB=CD,
∵BE是⊙O的直径,
∴,
∴AB=BC=CD,
∵CD∥AB,
∴四边形ABCD是菱形;
(2)∵∠AOF=3∠FOE,
设∠FOE=x,则∠AOF=3x,
∠AOD=∠FOE+∠AOF=4x,
∵OA=OF,
∴∠OAF=∠OFA=(180﹣3x)°,
∵OA=OB,
∴∠OAB=∠OBA=2x,
∴∠ABC=4x,
∵BC∥AD,
∴∠ABC+∠BAD=180°,
∴4x+2x+(180﹣3x)=180,
x=20°,
∴∠AOF=3x=60°,∠AOE=80°,
∴∠COF=80°×2﹣60°=100°,
∵OA=OF,
∴△AOF是等边三角形,
∴OF=AF=3,
∴的长==.
39.如图,AB是⊙O的直径,点D在⊙O上,∠DAB=45°,BC∥AD,CD∥AB.若⊙O的半径为1,求图中阴影部分的面积(结果保留π).
【分析】阴影部分的面积可由梯形OBCD和扇形OBD的面积差求得;扇形的半径和圆心角已求得,那么关键是求出梯形上底CD的长,可通过证四边形ABCD是平行四边形,得出CD=AB,由此可求出CD的长,即可得解.
【解答】解:∵BC∥AD,CD∥AB,
∴四边形ABCD是平行四边形,
∴CD=AB=2
∴S梯形OBCD==;
∴图中阴影部分的面积等于S梯形OBCD﹣S扇形OBD=﹣×π×12=﹣.
40.如图,已知⊙O半径为10cm,弦AB垂直平分半径OC,并交OC于点D.
(1)求弦AB的长;
(2)求弧AB的长,并求出图中阴影部分面积.
【分析】(1)先利用垂径定理得出AB=2BD,∠ODB=90°,OD=OC=5,进而根据勾股定理求出BD,即可得出结论;
(2)先利用锐角三角函数求出∠BOD=60°,最后利用扇形的弧长公式和扇形的面积公式即可得出结论.
【解答】解:(1)如图,⊙O半径为10cm,
∴OB=OC=10,
∵弦AB垂直平分半径OC,
∴AB=2BD,∠ODB=90°,OD=OC=5,
在Rt△BOD中,根据勾股定理得,BD==5,
∴AB=2BD=10cm;
(2)由(1)知,OD=5,
在Rt△BOD中,cos∠BOD==,
∴∠BOD=60°,
∵OC⊥AB,
∴∠AOB=2∠BOD=120°,
∴===cm,
S阴影=S扇形AOB﹣S△AOB=﹣AB×OD=﹣×=﹣25(cm2).
一.选择题(共20小题)
1.如图,AB是⊙O的直径,AB=10,P是半径OA上的一动点,PC⊥AB交⊙O于点C,在半径OB上取点Q,使得OQ=CP,DQ⊥AB交⊙O于点D,点C,D位于AB两侧,连接CD交AB于点F,点P从点A出发沿AO向终点O运动,在整个运动过程中,△CFP与△DFQ的面积和的变化情况是( )
A.一直减小 B.一直不变
C.先变大后变小 D.先变小后变大
2.如图中正方形、矩形、圆的面积相等,则周长L的大小关系是( )
A.LA>LB>LC B.LA<LB<LC C.LB>LC>LA D.LC<LA<LB
3.某品牌婴儿罐装奶粉圆形桶口如图所示,它的内直径(⊙O直径)为10cm,弧AB的度数约为90°,则弓形铁片ACB(阴影部分) 的面积约为( )
A.(π﹣)cm2 B.(π﹣25)cm2
C.(π﹣)cm2 D.(25π﹣)cm2
4.已知AB、CD是两个不同圆的弦,如AB=CD,那么与的关系是( )
A. B. C. D.不能确定
5.如图,AB是⊙O的直径,点C、D在圆上,若∠D=45°,则tan∠ABC等于( )
A. B. C.1 D.
6.如图所示,四边形ABCD为⊙O的内接四边形,∠BCD=120°,则∠BOD的大小是( )
A.80° B.120° C.100° D.90°
7.如图,AB为⊙O的直径,AB=10cm,弦CD⊥AB,垂足为E,且AE:EB=2:3,则AC=( )
A.3cm B.4cm C.cm D.cm
8.一个点到圆的最小距离为4cm,最大距离为9cm,则该圆的半径是( )
A.2.5cm或6.5cm B.2.5cm
C.6.5cm D.5cm或13cm
9.考虑下面六个命题(1)任意三点确定一个圆;(2)平分弦的直径垂直于弦,且平分这条弦所对的弧;(3)90°的圆周角所对的弦是直径;(4)同弧或等弧所对的圆周角相等;(5)相等的圆周角所对的弧相等.其中正确的命题有( )
A.2个 B.3个 C.4个 D.5个
10.已知:点A(0,4),B(0,﹣6),C为x轴正半轴上一点,且满足∠ACB=45°,则( )
A.△ABC外接圆的圆心在OC上
B.∠BAC=60°
C.△ABC外接圆的半径等于5
D.OC=12
11.已知圆O的半径为3cm,点P是直线l上的一点,且OP=3cm,则直线l与圆O的位置关系为( )
A.相切 B.相交 C.相离 D.不能确定
12.如图,点O′在第一象限,⊙O′与x轴相切于H点,与y轴相交于A(0,2),B(0,8),则点O′的坐标是( )
A.(6,4) B.(4,6) C.(5,4) D.(4,5)
13.如下图,已知⊙O的直径为AB,AC⊥AB于点A,BC与⊙O相交于点D,在AC上取一点E,使得ED=EA.下面四个结论:
①ED是⊙O的切线;②BC=2OE;③△BOD为等边三角形;④△EOD∽△CAD
正确的是( )
A.①② B.②④ C.①②④ D.①②③④
14.如图,直线l1∥l2,⊙O与l1和l2分别相切于点A和点B.点M和点N分别是l1和l2上的动点,MN沿l1和l2平移.⊙O的半径为1,∠1=60°.下列结论错误的是( )
A.
B.l1和l2的距离为2
C.若∠MON=90°,则MN与⊙O相切
D.若MN与⊙O相切,则
15.如图,PA、PB、DE分别与⊙O相切,若∠P=40°,则∠DOE等于( )度.
A.40 B.50 C.70 D.80
16.如图,⊙O是四边形ABCD的内切圆,下列结论一定正确的有( )个:
①AF=BG;②CG=CH;③AB+CD=AD+BC;④BG<CG.
A.1 B.2 C.3 D.4
17.如图,PAB为⊙O的割线,且PA=AB=3,PO交⊙O于点C,若PC=2,则⊙O的半径的长为( )
A. B. C. D.7
18.如图,点I是△ABC的内心,若∠AIB=125°,则∠C等于( )
A.65° B.70° C.75° D.80°
19.如图,有一个边长为2cm的正六边形纸片,若在该纸片上剪一个最大圆形,则这个圆形纸片的直径是( )
A.cm B.2cm C.2cm D.4cm
20.如图,在扇形AOB中,∠AOB=90°,点C为OA的中点,CE⊥OA交于点E,以点O为圆心,OC的长为半径作交OB于点D.若OA=4,则图中阴影部分的面积为( )
A.+ B.+2 C.+ D.2+
二.填空题(共9小题)
21.如图,在Rt△ABC中,AC=3,BC=4,分别以它的三边为直径向上作三个半圆,则阴影部分面积为 .(不取近似值)
22.如图,在坐标系中以原点为圆心,半径为2的圆,直线y=kx﹣(k+1)与⊙O有两个交点A、B,则AB的最短长度是 .
23.为改善市区人居环境,某市建设污水管网工程,已知圆柱形污水管的直径为50cm,截面如图所示,当管内污水的面宽AB=40cm时,污水的最大深度为 cm.
24.如图,⊙O是△ABC的外接圆,已知∠ABO=40°,则∠ACB的大小为 .
25.如图,四边形ABCD内接于⊙O,AB为⊙O的直径,点D为的中点,若∠B=50°,则∠A的度数为 度.
26.如图,在⊙O中,弦AB平分弦CD于E,若CD=8,AE:EB=1:4,则弦AB= .
27.已知点P在半径为5的⊙O外,如果设OP=x,那么x的取值范围是 .
28.若A(1,2),B(3,﹣3),C(x,y)三点可以确定一个圆,则x、y需要满足的条件是 .
29.△ABC的三边分别是3,4,5,则△ABC的外接圆的半径是 .
三.解答题(共11小题)
30.已知;如图,在⊙O中,C、D分别是半径OA、BO的中点,求证:AD=BC.
31.如图,⊙O中,直径CD⊥弦AB于E,AM⊥BC于M,交CD于N,连接AD.
(1)求证:AD=AN;
(2)若AB=8,ON=1,求⊙O的半径.
32.如图,一面墙上有一个矩形的门洞,现要将它改为一个圆弧形的门洞,圆弧所在的圆外接矩形,已知矩形的高AC=2米,宽CD=米.
(1)求此圆形门洞的半径;
(2)求要打掉墙体的面积.
33.如图,边长为2的正方形ABCD各边的延长线和反向延长线与⊙O的交点把⊙O分成8条相等的弧,则⊙O的半径是 .
34.如图,四边形ABCD是⊙O的内接四边形,=,AC为直径,DE⊥BC,垂足为E.
(1)求证:CD平分∠ACE;
(2)若AC=9,CE=3,求CD的长.
35.如图,以点O′(1,1)为圆心,OO′为半径画圆,判断点P(﹣1,1),点Q(1,0),点R(2,2)和⊙O′的位置关系.
36.如图,点O为Rt△ABC斜边AB上的一点,以OA为半径的⊙O与BC切于点D,与AC交于点E,连接AD.
(1)求证:AD平分∠BAC;
(2)若∠BAC=60°,OA=2,求阴影部分的面积(结果保留π).
37.如图,PA,PB分别为⊙O的切线,AC为直径,切点分别为A、B,∠P=70°,则∠C= .
38.如图,在⊙O上依次有A、B、C三点,BO的延长线交⊙O于E,,过点C作CD∥AB交BE的延长线于D,AD交⊙O于点F.
(1)求证:四边形ABCD是菱形;
(2)连接OA、OF,若∠AOF=3∠FOE且AF=3,求劣弧的长.
39.如图,AB是⊙O的直径,点D在⊙O上,∠DAB=45°,BC∥AD,CD∥AB.若⊙O的半径为1,求图中阴影部分的面积(结果保留π).
40.如图,已知⊙O半径为10cm,弦AB垂直平分半径OC,并交OC于点D.
(1)求弦AB的长;
(2)求弧AB的长,并求出图中阴影部分面积.
参考答案与试题解析
一.选择题(共20小题)
1.如图,AB是⊙O的直径,AB=10,P是半径OA上的一动点,PC⊥AB交⊙O于点C,在半径OB上取点Q,使得OQ=CP,DQ⊥AB交⊙O于点D,点C,D位于AB两侧,连接CD交AB于点F,点P从点A出发沿AO向终点O运动,在整个运动过程中,△CFP与△DFQ的面积和的变化情况是( )
A.一直减小 B.一直不变
C.先变大后变小 D.先变小后变大
【分析】连接OC,OD,PD,CQ.设PC=x,OP=y,OF=a,利用分割法求出阴影部分的面积,再求出a=y﹣x即可判断;
【解答】解:连接OC,OD,PD,CQ.设PC=x,OP=y,OF=a,
∵PC⊥AB,QD⊥AB,
∴∠CPO=∠OQD=90°,
∵PC=OQ,OC=OD,
∴Rt△OPC≌Rt△DQO,
∴OP=DQ=y,
∴S阴=S四边形PCQD﹣S△PFD﹣S△CFQ=(x+y)2﹣?(y﹣a)y﹣(x+a)x=xy+a(y﹣x),
∵PC∥DQ,
∴=,
∴=,
∴a=y﹣x,
∴S阴=xy+(y﹣x)(y﹣x)=(x2+y2)=
故选:B.
2.如图中正方形、矩形、圆的面积相等,则周长L的大小关系是( )
A.LA>LB>LC B.LA<LB<LC C.LB>LC>LA D.LC<LA<LB
【分析】设相同的面积为未知数,进而判断出相应的周长,比较即可.
【解答】解:设面积是S.
则正方形的边长是,则周长LA=4==4;
长方形的一边长x,则另一边长为,则周长LB=2(x+),
∵(x+)2≥0
∴x+≥2,
∴LB≥4,
即LB≥;
圆的半径为,LC=2π×=,
∵<,
∴LC<LA<LB.
故选:D.
3.某品牌婴儿罐装奶粉圆形桶口如图所示,它的内直径(⊙O直径)为10cm,弧AB的度数约为90°,则弓形铁片ACB(阴影部分) 的面积约为( )
A.(π﹣)cm2 B.(π﹣25)cm2
C.(π﹣)cm2 D.(25π﹣)cm2
【分析】连接OA、OB,根据已知求出OA=OB=5cm,∠BOA=90°,分别求出扇形BOA和△BOA的面积即可.
【解答】解:
连接OA、OB,
∵品牌婴儿罐装奶粉圆形桶口如图所示,它的内直径(⊙O直径)为10cm,弧AB的度数约为90°,
∴OA=OB=5cm,∠BOA=90°,
∴阴影部分的面积S=S扇形BOA﹣S△BOA=﹣=(π﹣)cm2,
故选:A.
4.已知AB、CD是两个不同圆的弦,如AB=CD,那么与的关系是( )
A. B. C. D.不能确定
【分析】根据在同圆和等圆中相等的弦所对的弧相等分析,从而得到答案.
【解答】解:在同圆和等圆中相等的弦所对的弧才会相等,要注意同圆和的条件,本题是两个不同的圆,所以无法判断两弦所对的弧的大小,故选D.
5.如图,AB是⊙O的直径,点C、D在圆上,若∠D=45°,则tan∠ABC等于( )
A. B. C.1 D.
【分析】连接AC,如图,根据圆周角定理得到∠ACB=90°,∠A=∠D=45°,则利用互余得到∠ABC=45°,然后根据特殊角的三角函数值求解.
【解答】解:连接AC,如图,
∵AB是⊙O的直径,
∴∠ACB=90°,
∵∠A=∠D=45°,
∴∠ABC=45°,
∴tan∠ABC=tan45°=1.
故选:C.
6.如图所示,四边形ABCD为⊙O的内接四边形,∠BCD=120°,则∠BOD的大小是( )
A.80° B.120° C.100° D.90°
【分析】根据圆内接四边形的性质求出∠A,再根据圆周角定理解答.
【解答】解:∵四边形ABCD为⊙O的内接四边形,
∴∠A=180°﹣∠BCD=60°,
由圆周角定理得,∠BOD=2∠A=120°,
故选:B.
7.如图,AB为⊙O的直径,AB=10cm,弦CD⊥AB,垂足为E,且AE:EB=2:3,则AC=( )
A.3cm B.4cm C.cm D.cm
【分析】由垂径定理得到CE=DE,又根据相交弦定理得到CE?ED=AE?EB,即CE2=AE?BE,可求得CE,再由勾股定理求出AC即可.
【解答】解:∵CD⊥AB,∴CE=DE,
∴CE2=AE?BE,
∵AB=10cm,且AE:EB=2:3,
∴AE=4cm,EB=6cm,
∴CE=2cm,
∴AC===2cm.
故选:D.
8.一个点到圆的最小距离为4cm,最大距离为9cm,则该圆的半径是( )
A.2.5cm或6.5cm B.2.5cm
C.6.5cm D.5cm或13cm
【分析】设此点为P点,圆为⊙O,最大距离为PB,最小距离为PA,有两种情况:①当此点在圆内;②当此点在圆外;分别求出半径值即可.
【解答】解:设此点为P点,圆为⊙O,最大距离为PB,最小距离为PA,则:
∵此点与圆心的连线所在的直线与圆的交点即为此点到圆心的最大、最小距离
∴有两种情况:
当此点在圆内时,如图所示,
半径OB=(PA+PB)÷2=6.5cm;
当此点在圆外时,如图所示,
半径OB=(PB﹣PA)÷2=2.5cm;
故圆的半径为2.5cm或6.5cm
故选:A.
9.考虑下面六个命题(1)任意三点确定一个圆;(2)平分弦的直径垂直于弦,且平分这条弦所对的弧;(3)90°的圆周角所对的弦是直径;(4)同弧或等弧所对的圆周角相等;(5)相等的圆周角所对的弧相等.其中正确的命题有( )
A.2个 B.3个 C.4个 D.5个
【分析】根据圆中的定理进行分析.
确定圆的定理:不在同一条直线上的三个点确定一个圆;
垂径定理的推论:平分弦(非直径)的直径垂直于弦,且平分这条弦所对的弧;
圆周角定理的推论:在同圆或等圆中,相等的圆周角所对的弧相等,同弧或等弧所对的圆周角相等;
90°的圆周角所对的弦是直径.
【解答】解:根据圆中的定理及其推论,知
(1)当三点共线的时候不能确定一个圆,故错误;
(2)当该弦是直径的时候,不一定能够垂直,故错误;
(3)和(4)根据圆周角定理的推论,故正确;
(5)必须在同圆或等圆中,故错误.
故选:A.
10.已知:点A(0,4),B(0,﹣6),C为x轴正半轴上一点,且满足∠ACB=45°,则( )
A.△ABC外接圆的圆心在OC上
B.∠BAC=60°
C.△ABC外接圆的半径等于5
D.OC=12
【分析】构造含有90°圆心角的⊙P,则⊙P与x轴的交点即为所求的点C.根据△PBA为等腰直角三角形,可得OF=PE=5,根据勾股定理得:CF=7,进而得出OC.
【解答】解:设线段BA的中点为E,
∵点A(0,4),B(0,﹣6),
∴AB=10,E(0,﹣1).
如图所示,过点E在第四象限作EP⊥BA,且EP=AB=5,则
易知△PBA为等腰直角三角形,∠BPA=90°,PA=PB=5;
以点P为圆心,PA(或PB)长为半径作⊙P,与y轴的正半轴交于点C,
∵∠BCA为⊙P的圆周角,
∴∠BCA=∠BPA=45°,即则点C即为所求.
过点P作PF⊥x轴于点F,则OF=PE=5,PF=OE=1,
在Rt△PFC中,PF=1,PC=5,
由勾股定理得:CF==7,
∴OC=OF+CF=5+7=12,
故选:D.
11.已知圆O的半径为3cm,点P是直线l上的一点,且OP=3cm,则直线l与圆O的位置关系为( )
A.相切 B.相交 C.相离 D.不能确定
【分析】直线和圆的位置关系与数量之间的联系:
若d<r,则直线与圆相交;若d=r,则直线于圆相切;若d>r,则直线与圆相离.
【解答】解:因为垂线段最短,所以圆心到直线的距离小于等于3.
此时和半径3的大小不确定,则直线和圆相交、相切都有可能.
故选:D.
12.如图,点O′在第一象限,⊙O′与x轴相切于H点,与y轴相交于A(0,2),B(0,8),则点O′的坐标是( )
A.(6,4) B.(4,6) C.(5,4) D.(4,5)
【分析】过O'作O'C⊥AB于点C,过O'作O'D⊥x轴于点D,由切线的性质可求得O'D的长,则可得O'B的长,由垂径定理可求得CB的长,在Rt△O'BC中,由勾股定理可求得O'C的长,从而可求得O'点坐标.
【解答】解:
如图,过O'作O'C⊥AB于点C,过O'作O'D⊥x轴于点D,连接O'B,
∵O'为圆心,
∴AC=BC,
∵A(0,2),B(0,8),
∴AB=8﹣2=6,
∴AC=BC=3,
∴OC=8﹣3=5,
∵⊙O'与x轴相切,
∴O'D=O'B=OC=5,
在Rt△O'BC中,由勾股定理可得O'C==4,
∴P点坐标为(4,5),
故选:D.
13.如下图,已知⊙O的直径为AB,AC⊥AB于点A,BC与⊙O相交于点D,在AC上取一点E,使得ED=EA.下面四个结论:
①ED是⊙O的切线;②BC=2OE;③△BOD为等边三角形;④△EOD∽△CAD
正确的是( )
A.①② B.②④ C.①②④ D.①②③④
【分析】如图,通过证明△AOE≌△DOE得到∠OAE=∠ODE=90°,易证得ED是⊙O的切线;证得OE是△ABC的中位线,证得BC=2OE,由OE∥BC,证得∠AEO=∠C,通过三角形全等证得∠DEO=∠C,∠ODE=∠OAE=90°,从而∠ODE=∠ADC=90°,从而证得△EOD∽△CAD.
【解答】证明:如图,连接OD.
∵AC⊥AB,
∴∠BAC=90°,即∠OAE=90°.
在△AOE与△DOE中,
,
∴△AOE≌△DOE(SSS),
∴∠OAE=∠ODE=90°,即OD⊥ED.
又∵OD是⊙O的半径,
∴ED是⊙O的切线;
∵AB是直径,
∴AD⊥BC,
∴∠DAE+∠C=90°,
∵AE=DE,
∴∠DAE=∠ADE,
∵∠ADE+∠EDC=90°,
∴∠EDC=∠C,
∴DE=EC,
∴AE=EC,
∵OA=OB,
∴OE∥BC,BC=2OE,
∴∠AEO=∠C,
∵△AOE≌△DOE,
∴∠DEO=∠C,∠ODE=∠OAE=90°,
∴∠ODE=ADC=90°,
∴△EOD∽△CAD.
∴正确的①②④,
故选:C.
14.如图,直线l1∥l2,⊙O与l1和l2分别相切于点A和点B.点M和点N分别是l1和l2上的动点,MN沿l1和l2平移.⊙O的半径为1,∠1=60°.下列结论错误的是( )
A.
B.l1和l2的距离为2
C.若∠MON=90°,则MN与⊙O相切
D.若MN与⊙O相切,则
【分析】首先过点N作NC⊥AM于点C,直线l1∥l2,⊙O与l1和l2分别相切于点A和点B,⊙O的半径为1,易求得MN==,l1和l2的距离为2;
若∠MON=90°,连接NO并延长交MA于点C,易证得CO=NO,继而可得即O到MN的距离等于半径,可证得MN与⊙O相切;
由题意可求得若MN与⊙O相切,则AM=或.
【解答】解:如图1,过点N作NC⊥AM于点C,
∵直线l1∥l2,⊙O与l1和l2分别相切于点A和点B,⊙O的半径为1,
∴CN=AB=2,
∵∠1=60°,
∴MN==,
故A与B正确;
如图3,
若∠MON=90°,连接NO并延长交MA于点C,则△AOC≌△BON,
故CO=NO,△MON≌△MOM′,故MN上的高为1,即O到MN的距离等于半径.
故C正确;
如图2,∵MN是切线,⊙O与l1和l2分别相切于点A和点B,
∴∠AMO=∠1=30°,
∴AM=;
∵∠AM′O=60°,
∴AM′=,
∴若MN与⊙O相切,则AM=或;
故D错误.
故选:D.
15.如图,PA、PB、DE分别与⊙O相切,若∠P=40°,则∠DOE等于( )度.
A.40 B.50 C.70 D.80
【分析】连接OA、OB、OF,由切线的性质得∠AOB=140°,再由切线长定理求得∠DOE的度数.
【解答】解:连接OA、OB、OF,
∵∠P=40°,
∴∠AOB=140°,
∵PA、PB、DE分别与⊙O相切,
∴∠AOD=∠FOD,∠BOE=∠FOE,
∴∠DOE=∠AOB=×140°=70°.
故选:C.
16.如图,⊙O是四边形ABCD的内切圆,下列结论一定正确的有( )个:
①AF=BG;②CG=CH;③AB+CD=AD+BC;④BG<CG.
A.1 B.2 C.3 D.4
【分析】根据切线长定理得到AF=AE,BF=BG,CG=CH,DH=DE,则AB+CD=AF+BF+CH+DH=AE+BG+CG+DE=AD+BC.
【解答】解:∵⊙O是四边形ABCD的内切圆,
∴AF=AE,BF=BG,CG=CH,DH=DE,
∴AB+CD=AF+BF+CH+DH=AE+BG+CG+DE=AD+BC.
①AF=BG;④BG<CG无法判断.
正确的有②③
故选:B.
17.如图,PAB为⊙O的割线,且PA=AB=3,PO交⊙O于点C,若PC=2,则⊙O的半径的长为( )
A. B. C. D.7
【分析】延长PO交圆于点D,利用割线定理求解;也可作OD⊥AB于D,根据垂径定理和勾股定理求解.
【解答】解法一:延长PO交圆于点D
利用割线定理可知PA?PB=PC?PD,求得PD=9,
所以CD=7,半径=3.5.
解法二:作OD⊥AB于D,根据垂径定理和勾股定理求解.
故选:A.
18.如图,点I是△ABC的内心,若∠AIB=125°,则∠C等于( )
A.65° B.70° C.75° D.80°
【分析】根据三角形内角和定理得到∠IAB+∠IBA=55°,根据内心的概念得到∠CAB+∠ABC=110°,根据三角形内角和定理计算即可.
【解答】解:∵∠AIB=125°,
∴∠IAB+∠IBA=55°,
∵点I是△ABC的内心,
∴∠IAB=∠CAB,∠IBA=∠ABC,
∴∠CAB+∠ABC=110°,
∴∠C=180°﹣(∠CAB+∠ABC)=70°,
故选:B.
19.如图,有一个边长为2cm的正六边形纸片,若在该纸片上剪一个最大圆形,则这个圆形纸片的直径是( )
A.cm B.2cm C.2cm D.4cm
【分析】根据题意画出图形,再根据正多边形圆心角的求法求出∠AOB的度数,最后根据等腰三角形及直角三角形的性质解答即可.
【解答】解:如图所示,正六边形的边长为2cm,OG⊥BC,
∵六边形ABCDEF是正六边形,
∴∠BOC=360°÷6=60°,
∵OB=OC,OG⊥BC,
∴∠BOG=∠COG==30°,
∵OG⊥BC,OB=OC,BC=2cm,
∴BG=BC=×2=1cm,
∴OB==2cm,
∴OG===,
∴圆形纸片的直径为2cm,
故选:B.
20.如图,在扇形AOB中,∠AOB=90°,点C为OA的中点,CE⊥OA交于点E,以点O为圆心,OC的长为半径作交OB于点D.若OA=4,则图中阴影部分的面积为( )
A.+ B.+2 C.+ D.2+
【分析】连接OE、AE,根据点C为OC的中点可得∠CEO=30°,继而可得△AEO为等边三角形,求出扇形AOE的面积,最后用扇形AOB的面积减去扇形COD的面积,再减去S空白AEC即可求出阴影部分的面积.
【解答】解:连接OE、AE,
∵点C为OA的中点,
∴EO=2OC,
∴∠CEO=30°,∠EOC=60°,
∴△AEO为等边三角形,
∴S扇形AOE==,
∴S阴影=S扇形AOB﹣S扇形COD﹣(S扇形AOE﹣S△COE)
=﹣﹣(﹣)
=4π﹣π﹣+2
=+2
故选:B.
二.填空题(共9小题)
21.如图,在Rt△ABC中,AC=3,BC=4,分别以它的三边为直径向上作三个半圆,则阴影部分面积为 6 .(不取近似值)
【分析】阴影部分的面积等于中间直角三角形的面积加上两个小半圆的面积,减去其中下面面积较大的半圆的面积.
【解答】解:以BC为直径的半圆的面积是2π,以AC为直径的半圆的面积是π()2=,以AB为直径的面积是×π()2=,△ABC的面积是6,因而阴影部分的面积是2π++6﹣=6.
22.如图,在坐标系中以原点为圆心,半径为2的圆,直线y=kx﹣(k+1)与⊙O有两个交点A、B,则AB的最短长度是 2 .
【分析】易知直线y=kx﹣3k+4过定点D(1,﹣1),运用勾股定理可求出OD,由于过圆内定点D的所有弦中,与OD垂直的弦最短,因此只需运用垂径定理及勾股定理就可解决问题
【解答】解:∵直线y=kx﹣(k+1)可化为y=(x﹣1)k﹣1,
∴此直线恒过点(1,﹣1).
过点D作DH⊥x轴于点H,
∵OH=1,DH=1,OD===.
∵OB=2,
∴BD===,
∴AB=2.
故答案为:2.
23.为改善市区人居环境,某市建设污水管网工程,已知圆柱形污水管的直径为50cm,截面如图所示,当管内污水的面宽AB=40cm时,污水的最大深度为 10 cm.
【分析】根据垂径定理和勾股定理求解.
【解答】解:如图1,作弦的弦心距,连接一条半径,
根据垂径定理,得半弦是20cm,
根据勾股定理,得弦心距是15cm,
则污水的最大深度是25﹣15=10cm;
故答案为10.
24.如图,⊙O是△ABC的外接圆,已知∠ABO=40°,则∠ACB的大小为 130° .
【分析】根据等腰三角形的性质、三角形内角和定理求出∠AOB,根据圆周角定理计算即可.
【解答】解:∵OA=OB,∠ABO=40°,
∴∠AOB=100°,
∴∠ACB=×(360°﹣100°)=130°,
故答案为:130°.
25.如图,四边形ABCD内接于⊙O,AB为⊙O的直径,点D为的中点,若∠B=50°,则∠A的度数为 65 度.
【分析】连接OD、OC,根据圆周角定理求出∠AOC=100°,根据三角形内角和定理计算即可.
【解答】解:连接OD、OC,
∵点D为的中点,
∴∠AOD=∠COD,
∵∠B=50°,
∴∠AOC=100°,
∴∠AOD=∠COD=50°,
∴∠A=∠ODA=65°,
故答案为:65.
26.如图,在⊙O中,弦AB平分弦CD于E,若CD=8,AE:EB=1:4,则弦AB= 10 .
【分析】设AE=x,则EB=4x,由弦AB平分弦CD于E,得到CE=DE=CD=4,再根据相交弦定理得x?4x=4?4,解得x=2或x=﹣2(舍去),然后计算5x即可.
【解答】解:设AE=x,则EB=4x,
∵弦AB平分弦CD于E,
∴CE=DE=CD=×8=4,
∵AE?BE=CE?DE,
即x?4x=4?4,解得x=2或x=﹣2(舍去),
∴AB=AE+BE=5x=10.
故答案为10.
27.已知点P在半径为5的⊙O外,如果设OP=x,那么x的取值范围是 x>5 .
【分析】根据点在圆外的判断方法得到x的取值范围.
【解答】解:∵点P在半径为5的⊙O外,
∴OP>5,即x>5.
故答案为x>5.
28.若A(1,2),B(3,﹣3),C(x,y)三点可以确定一个圆,则x、y需要满足的条件是 5x+2y≠9 .
【分析】能确定一个圆就是不在同一直线上,首先确定直线AB的解析式,然后点C不满足求得的直线即可;
【解答】解:设直线AB的解析式为y=kx+b,
∵A(1,2),B(3,﹣3),
∴,
解得:k=﹣,b=,
∴直线AB的解析式为y=﹣x+,
∵点A(1,2),B(3,﹣3),C(x,y)三点可以确定一个圆时,
∴点C不在直线AB上,
∴5x+2y≠9,
故答案为:5x+2y≠9.
29.△ABC的三边分别是3,4,5,则△ABC的外接圆的半径是 .
【分析】根据勾股定理逆定理得到△ABC是直角三角形,根据圆周角定理解答.
【解答】解:∵32+42=25,52=25,
∴32+42=52,
∴△ABC是直角三角形,
∴△ABC的外接圆的半径为,
故答案为:.
三.解答题(共11小题)
30.已知;如图,在⊙O中,C、D分别是半径OA、BO的中点,求证:AD=BC.
【分析】首先证明OC=OD,再证明△OCB≌△ODA,进而得到AD=BC.
【解答】解:∵OA、OB是⊙O的两条半径,
∴AO=BO,
∵C、D分别是半径OA、BO的中点,
∴OC=OD,
在△OCB和△ODA中,
,
∴△OCB≌△ODA(SAS),
∴AD=BC.
31.如图,⊙O中,直径CD⊥弦AB于E,AM⊥BC于M,交CD于N,连接AD.
(1)求证:AD=AN;
(2)若AB=8,ON=1,求⊙O的半径.
【分析】(1)先根据圆周角定理得出∠BAD=∠BCD,再由直角三角形的性质得出∠ANE=∠CNM,故可得出∠BCD=∠BAM,由全等三角形的判定定理得出△ANE≌△ADE,故可得出结论;
(2)先根据垂径定理求出AE的长,设NE=x,则OE=x﹣1,NE=ED=x,r=OD=OE+ED=2x﹣1连结AO,则AO=OD=2x﹣1,在Rt△AOE中根据勾股定理可得出x的值,进而得出结论.
【解答】(1)证明:∵CD⊥AB
∴∠CEB=90°
∴∠C+∠B=90°,
同理∠C+∠CNM=90°
∴∠CNM=∠B
∵∠CNM=∠AND
∴∠AND=∠B,
∵,
∴∠D=∠B,
∴∠AND=∠D,
∴AN=AD;
(2)解:设OE的长为x,连接OA
∵AN=AD,CD⊥AB
∴DE=NE=x+1,
∴OD=OE+ED=x+x+1=2x+1,
∴OA=OD=2x+1,
∴在Rt△OAE中OE2+AE2=OA2,
∴x2+42=(2x+1)2.
解得x=或x=﹣3(不合题意,舍去),
∴OA=2x+1=2×+1=,
即⊙O的半径为.
32.如图,一面墙上有一个矩形的门洞,现要将它改为一个圆弧形的门洞,圆弧所在的圆外接矩形,已知矩形的高AC=2米,宽CD=米.
(1)求此圆形门洞的半径;
(2)求要打掉墙体的面积.
【分析】(1)先证得BC是直径,在直角三角形BCD中,由BD与CD的长,利用勾股定理求出BC的长,即可求得半径;
(2)打掉墙体的面积=2(S扇形OAC﹣S△AOC)+S扇形OAB﹣S△AOB,根据扇形的面积和三角形的面积求出即可.
【解答】解:(1)连结AD、BC,
∵∠BDC=90°,
∴BC是直径,
∴BC==
∴圆形门洞的半径为.
(2)取圆心O,连结OA.由上题可知,OA=OB=AB=,
∴△AOB是正三角形,
∴∠AOB=60°,∠AOC=120°,
∴S△AOB=,S△AOC=
∴S=2(S扇形OAC﹣S△AOC)+S扇形OAB﹣S△AOB
=2(﹣)+(﹣)
=π﹣
∴打掉墙体面积为π﹣平方米.
33.如图,边长为2的正方形ABCD各边的延长线和反向延长线与⊙O的交点把⊙O分成8条相等的弧,则⊙O的半径是 .
【分析】连接MN,EW,MW,QM,证四边形QMNW和BWNC是矩形,推出WN=QM=EW=2,根据勾股定理求出BE=BW=,在Rt△MQW中根据勾股定理求出半径即可.
【解答】解:连接MN,EW,MW,QM,
∵弧QM=弧WN,
∴QM∥WN,QM=WN,∠WNM=×360°×4×=90°,
∴四边形QMNW是矩形,
∴O在MW上,
∵正方形ABCD,
∴∠WBC=∠BCN=90°,
∴四边形BCNW是矩形,
∴WN=QM=EW=2,
∵∠BEW=∠EWB=45°,
∴由勾股定理得:EB=BW=,
同理AQ=,
设圆O的半径是r,
在Rt△MQW中,由勾股定理得:MQ2+QW2=MW2,
∴22+=(2r)2
r=,
故答案为:.
34.如图,四边形ABCD是⊙O的内接四边形,=,AC为直径,DE⊥BC,垂足为E.
(1)求证:CD平分∠ACE;
(2)若AC=9,CE=3,求CD的长.
【分析】(1)根据圆内接四边形的性质得到∠DCE=∠BAD,根据圆周角定理得到∠ACD=∠BAD,证明即可;
(2)证明△DCE∽△ACD,根据相似三角形的性质列出比例式,计算即可.
【解答】(1)证明:∵四边形ABCD是⊙O内接四边形,
∴∠BAD+∠BCD=180°,
∵∠BCD+∠DCE=180°,
∴∠DCE=∠BAD,
∵=,
∴∠BAD=∠ACD,
∴∠DCE=∠ACD,
∴CD平分∠ACE;
(2)解:∵AC为直径,
∴∠ADC=90°,
∵DE⊥BC,
∴∠DEC=90°,
∴∠DEC=∠ADC,
∵∠DCE=∠ACD,
∴△DCE∽△ACD,
∴=,即=,
∴CD=3.
35.如图,以点O′(1,1)为圆心,OO′为半径画圆,判断点P(﹣1,1),点Q(1,0),点R(2,2)和⊙O′的位置关系.
【分析】点与圆的位置关系由三种:设点到圆心的距离为d,则当d=r时,点在圆上;当d>r时,点在圆外;当d<r时,点在圆内.
【解答】解:∵OO′=r==,O′P==2
同理可得:O′Q=1,O′R=,
∴O′P>r,点P在⊙O′外;
O′Q<r,点Q在⊙O′内;
O′R=r,点R在⊙O′上.
36.如图,点O为Rt△ABC斜边AB上的一点,以OA为半径的⊙O与BC切于点D,与AC交于点E,连接AD.
(1)求证:AD平分∠BAC;
(2)若∠BAC=60°,OA=2,求阴影部分的面积(结果保留π).
【分析】(1)由Rt△ABC中,∠C=90°,⊙O切BC于D,易证得AC∥OD,继而证得AD平分∠CAB.
(2)如图,连接ED,根据(1)中AC∥OD和菱形的判定与性质得到四边形AEDO是菱形,则△AEM≌△DMO,则图中阴影部分的面积=扇形EOD的面积.
【解答】(1)证明:∵⊙O切BC于D,
∴OD⊥BC,
∵AC⊥BC,
∴AC∥OD,
∴∠CAD=∠ADO,
∵OA=OD,
∴∠OAD=∠ADO,
∴∠OAD=∠CAD,
即AD平分∠CAB;
(2)设EO与AD交于点M,连接ED.
∵∠BAC=60°,OA=OE,
∴△AEO是等边三角形,
∴AE=OA,∠AOE=60°,
∴AE=AO=OD,
又由(1)知,AC∥OD即AE∥OD,
∴四边形AEDO是菱形,则△AEM≌△DMO,∠EOD=60°,
∴S△AEM=S△DMO,
∴S阴影=S扇形EOD==π.
37.如图,PA,PB分别为⊙O的切线,AC为直径,切点分别为A、B,∠P=70°,则∠C= 55° .
【分析】由切线长定理,得△PAB为等腰三角形,可求得∠PAB的度数,再由切线的性质求出∠OAB,再由直径所对的圆周角等于90°和三角形的内角和定理,求得∠C即可.
【解答】解:∵PA,PB分别为⊙O的切线,∴PA=PB,
∵∠P=70°,∴∠PAB=(180°﹣70°)=55°,
∴∠OAB=90°﹣55°=35°,
∵AC为直径,∴∠ABC=90°,
∴∠C=180°﹣90°﹣35°
=55°,
故答案为55°.
38.如图,在⊙O上依次有A、B、C三点,BO的延长线交⊙O于E,,过点C作CD∥AB交BE的延长线于D,AD交⊙O于点F.
(1)求证:四边形ABCD是菱形;
(2)连接OA、OF,若∠AOF=3∠FOE且AF=3,求劣弧的长.
【分析】(1)先根据圆的性质得:∠CBD=∠ABD,由平行线的性质得:∠ABD=∠CDB,根据直径和等式的性质得:,由一组对边平行且相等可得四边形ABCD是平行四边形,由AB=BC可得结论;
(2)先设∠FOE=x,则∠AOF=3x,根据∠ABC+∠BAD=180°,列方程得:4x+2x+(180﹣3x)=180,求出x的值,接着求所对的圆心角和半径的长,根据弧长公式可得结论.
【解答】(1)证明:∵,
∴∠CBD=∠ABD,
∵CD∥AB,
∴∠ABD=∠CDB,
∴∠CBD=∠CDB,
∴CB=CD,
∵BE是⊙O的直径,
∴,
∴AB=BC=CD,
∵CD∥AB,
∴四边形ABCD是菱形;
(2)∵∠AOF=3∠FOE,
设∠FOE=x,则∠AOF=3x,
∠AOD=∠FOE+∠AOF=4x,
∵OA=OF,
∴∠OAF=∠OFA=(180﹣3x)°,
∵OA=OB,
∴∠OAB=∠OBA=2x,
∴∠ABC=4x,
∵BC∥AD,
∴∠ABC+∠BAD=180°,
∴4x+2x+(180﹣3x)=180,
x=20°,
∴∠AOF=3x=60°,∠AOE=80°,
∴∠COF=80°×2﹣60°=100°,
∵OA=OF,
∴△AOF是等边三角形,
∴OF=AF=3,
∴的长==.
39.如图,AB是⊙O的直径,点D在⊙O上,∠DAB=45°,BC∥AD,CD∥AB.若⊙O的半径为1,求图中阴影部分的面积(结果保留π).
【分析】阴影部分的面积可由梯形OBCD和扇形OBD的面积差求得;扇形的半径和圆心角已求得,那么关键是求出梯形上底CD的长,可通过证四边形ABCD是平行四边形,得出CD=AB,由此可求出CD的长,即可得解.
【解答】解:∵BC∥AD,CD∥AB,
∴四边形ABCD是平行四边形,
∴CD=AB=2
∴S梯形OBCD==;
∴图中阴影部分的面积等于S梯形OBCD﹣S扇形OBD=﹣×π×12=﹣.
40.如图,已知⊙O半径为10cm,弦AB垂直平分半径OC,并交OC于点D.
(1)求弦AB的长;
(2)求弧AB的长,并求出图中阴影部分面积.
【分析】(1)先利用垂径定理得出AB=2BD,∠ODB=90°,OD=OC=5,进而根据勾股定理求出BD,即可得出结论;
(2)先利用锐角三角函数求出∠BOD=60°,最后利用扇形的弧长公式和扇形的面积公式即可得出结论.
【解答】解:(1)如图,⊙O半径为10cm,
∴OB=OC=10,
∵弦AB垂直平分半径OC,
∴AB=2BD,∠ODB=90°,OD=OC=5,
在Rt△BOD中,根据勾股定理得,BD==5,
∴AB=2BD=10cm;
(2)由(1)知,OD=5,
在Rt△BOD中,cos∠BOD==,
∴∠BOD=60°,
∵OC⊥AB,
∴∠AOB=2∠BOD=120°,
∴===cm,
S阴影=S扇形AOB﹣S△AOB=﹣AB×OD=﹣×=﹣25(cm2).
