【北师大版七年级数学下册同步训练】2.3 平行线的性质同步训练(含解析)
文档属性
| 名称 | 【北师大版七年级数学下册同步训练】2.3 平行线的性质同步训练(含解析) |  | |
| 格式 | zip | ||
| 文件大小 | 686.4KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-02-13 13:46:22 | ||
图片预览



文档简介
2.3平行线的性质同步训练
学校:___________姓名:___________班级:___________考号:___________
一、单选题
1.如图,已知∠1=∠2,∠3=65°,那么∠4的度数是( )
A.55° B.95° C.115° D.145°
2.在、两座工厂之间要修建一条笔直的公路,从地测得地的走向是南偏东,现、两地要同时开工,若干天后,公路准确对接,则地所修公路的走向应该是( )
A.北偏西 B.南偏东 C.西偏北 D.北偏西
3.如图,直线a∥b,直线AB⊥AC,若∠1=50°,则∠2的度数为
A.50° B.45° C.30° D.40°
4.如图,已知直线a、b被直线c所截,a∥b,∠1=130°,则 ∠2=( )
A.130° B.50° C.40° D.60°
5.已知直线m∥n,将一块含30°角的直角三角板ABC按如图方式放置(∠ABC=30°),其中A,B两点分别落在直线m,n上,若∠1=20°,则∠2的度数为( )
A.20° B.30° C.45° D.50°
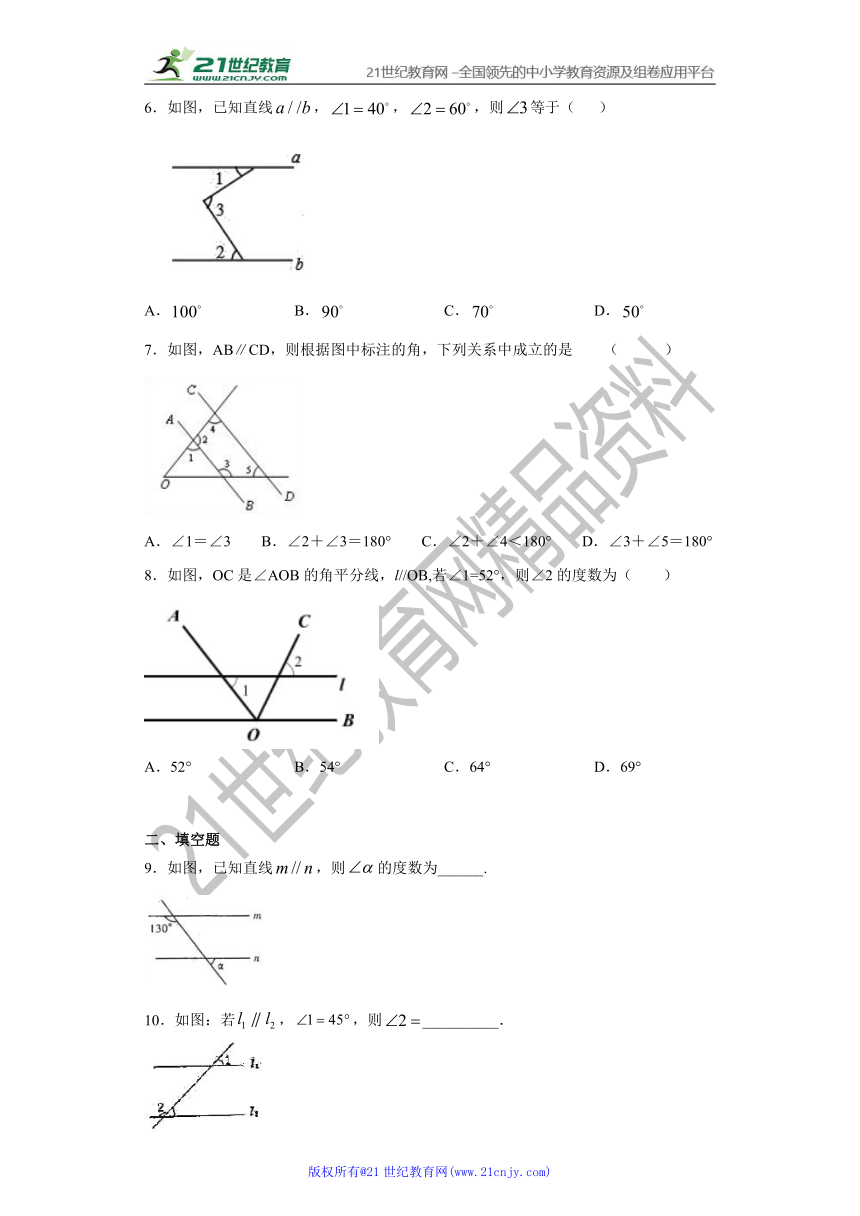
6.如图,已知直线,,,则等于( )
A. B. C. D.
7.如图,AB∥CD,则根据图中标注的角,下列关系中成立的是 ( )
A.∠1=∠3 B.∠2+∠3=180° C.∠2+∠4<180° D.∠3+∠5=180°
8.如图,OC是∠AOB的角平分线,l//OB,若∠1=52°,则∠2的度数为( )
A.52° B.54° C.64° D.69°
二、填空题
9.如图,已知直线,则的度数为______.
10.如图:若,,则__________.
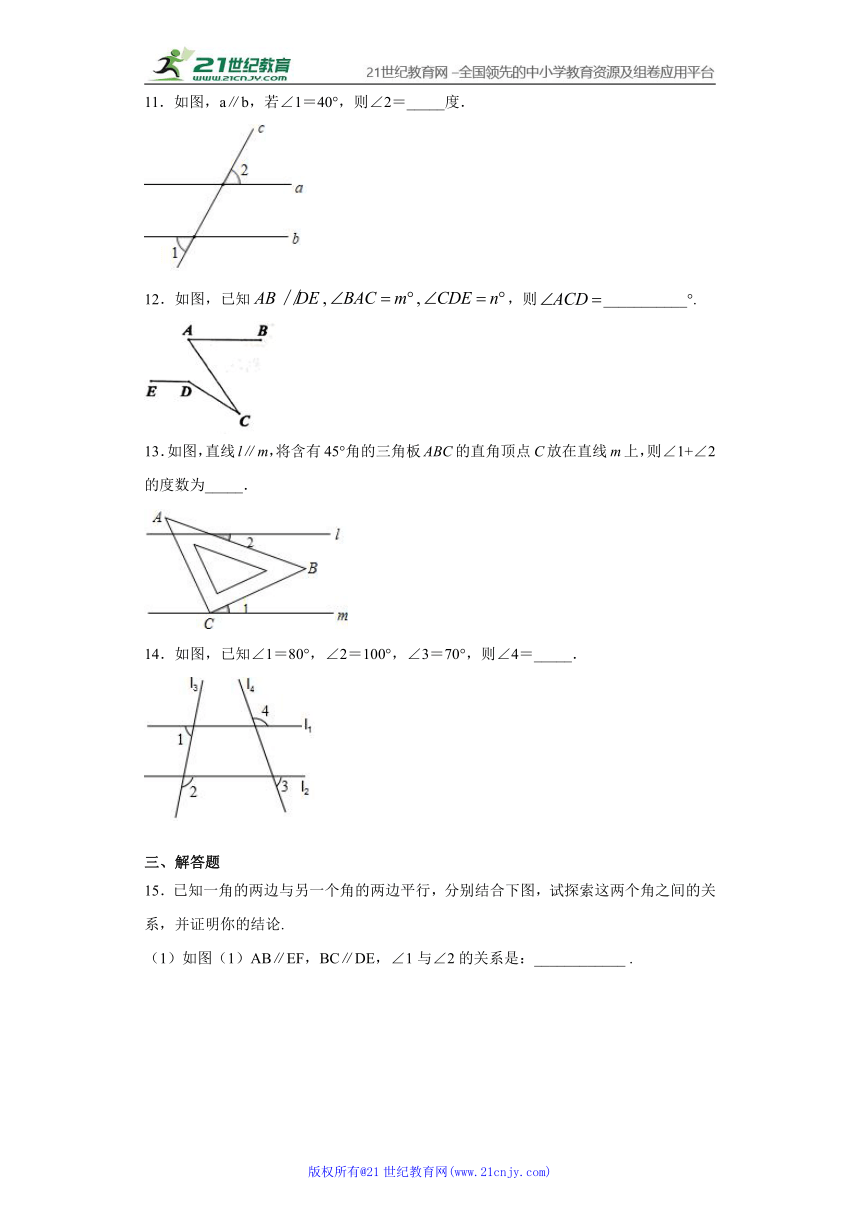
11.如图,a∥b,若∠1=40°,则∠2=_____度.
12.如图,已知,则___________°.
13.如图,直线l∥m,将含有45°角的三角板ABC的直角顶点C放在直线m上,则∠1+∠2的度数为_____.
14.如图,已知∠1=80°,∠2=100°,∠3=70°,则∠4=_____.
三、解答题
15.已知一角的两边与另一个角的两边平行,分别结合下图,试探索这两个角之间的关系,并证明你的结论.
(1)如图(1)AB∥EF,BC∥DE,∠1与∠2的关系是:____________ .
(2)如图(2)AB∥EF,BC∥DE, ∠1与∠2的关系是:____________
(3)经过上述证明,我们可以得到一个真命题:如果____ _____,那么____________.
(4)若两个角的两边互相平行,且一个角比另一个角的2倍少30°,则这两个角分别是多少度?
16.如图,在下列解答中,填空或填写适当的理由:
(1),(已知)
______________.(___________________________________________)
________________(______________________________________)
(2)_______,(已知)
;(___________________________________)
(3)_______________,(已知)
__________________________.(_______________________________)
17.如图,,平分.若,求的度数。根据提示将解题过程补充完整.
解:(平角),
又(已知),
,(_________)
(_________),(两直线平行,同旁内角互补)
,
(_________)
平分,
(_________).(角平分线的定义)
,
(_________)(两直线平行,内错角相等)
18.如图,已知和,在边上,且,为的角平分线,若,,求的度数.
参考答案
1.C
【解析】
【分析】
根据平行线的判定得出a∥b,根据平行线的性质得出∠4+∠5=180°,求出∠5即可.
【详解】
解:
∠1=∠2,
∴a∥b,
∴∠4+∠5=180°
∠3=65°
∴∠5=∠3=65°
∴∠4=180°-65°=115°
故选C.
【点睛】
本题考查平行线的性质和判定,能灵活运用定理进行分析推理是解此题的关键.
2.A
【解析】
如图,连接AB,
由题意得:∠CAB=52°,
∵DB∥AC,
∴∠CAB=∠ABD=52°,
∴B地所修公路走向应该是北偏西52°.
故选A.
点睛:本题结合方位角、平行线的性质解题.
3.D
【解析】
【分析】
根据两直线平行,内错角相等可得∠3=∠1,根据垂直的定义和余角的定义计算得到∠2.
【详解】
解:∵直线a∥b,∠1=50°, ∴∠1=∠3=50°, ∵AB⊥AC, ∴∠2+∠3=90°. ∴∠2=40°. 故选:D.
【点睛】
本题考查平行线的性质以及垂直的定义,属于中考常考题.
4.B
【解析】
【分析】
先根据邻补角的定义求出∠3,再利用两直线平行,同位角相等解答即可.
【详解】
解:如图
∵∠1=30°, ∴∠3=180°?∠1=180°?130°=50°, ∵a//b, ∴∠2=∠3=50°, 故答案为50°.
【点睛】
本题考查了平行线的性质,邻补角的定义,熟记性质是解题的关键.
5.D
【解析】
【分析】
根据两直线平行,内错角相等计算即可.
【详解】
因为m∥n,所以∠2=∠1+30°,所以∠2=30°+20°=50°,故选D.
【点睛】
本题主要考查平行线的性质,清楚两直线平行,内错角相等是解答本题的关键.
6.A
【解析】
【分析】
先过点C作CD∥a,根据平行于同一直线的两条直线互相平行,即可得CD∥a∥b,根据两直线平行,内错角相等,即可求得∠ACB的度数.
【详解】
如图,过点C作CD∥a.
∵a∥b,∴CD∥a∥b,∴∠ACD=∠1=40°,∠BCD=∠2=60°,∴∠ACB=∠ACD+∠BCD=100°.
故选A.
【点睛】
本题考查了平行线的性质.正确作出辅助线是解答本题的关键.
7.D
【解析】
试题分析:根据平行线的性质对各选项分析判断利用排除法求解:
A、∵OC与OD不平行,∴∠1=∠3不成立,故本选项错误;
B、∵OC与OD不平行,∴∠2+∠3=180°不成立,故本选项错误;
C、∵AB∥CD,∴∠2+∠4=180°,故本选项错误;
D、∵AB∥CD,∴∠3+∠5=180°,故本选项正确.
故选D.
考点:平行线的性质.
8.C
【解析】
【分析】
先根据两直线平行,同旁内角互补求出∠AOB=128°,再根据角平分线的定义得到∠BOC=64°,继而根据平行线的性质即可求得答案.
【详解】
∵l//OB,
∴∠1+∠AOB=180°,
∴∠AOB=128°,
∵OC平分∠AOB,
∴∠BOC=64°,
又∵l//OB,
∴∠2=∠BOC=64°,
故选C.
【点睛】
本题考查了平行线的性质,角平分线的定义,熟练掌握平行线的性质是解本题的关键.
9.50°
【解析】
【分析】
如图所示(见解析),由可得,,又因和角互补,则,从而可得.
【详解】
画图如下所示:
(两直线平行,同位角相等)
又和角互补
.
故的度数为.
【点睛】
本题考查了角互补的定义、平行线的性质,属于基础题型.平行线的性质有:(1)两直线平行,同位角相等;(2)两直线平行,内错角相等;(3)两直线平行,同旁内角互补.
10.
【解析】
【分析】
根据平行线的性质,得∠1的同位角是45°,再根据邻补角的定义,得:∠2=180°-45°=135°.
【详解】
∵∥,,
∴∠1的同位角是,
∴∠2.
故答案为:
【点睛】
考查平行线的性质,掌握两直线平行,同位角相等是解题的关键.
11.40
【解析】
【分析】
直接利用平行线的性质结合对顶角的性质分析得出答案.
【详解】
解:
∵∠1=40°,
∴∠1=∠3=40°
∵a∥b,
∴∠2=∠3=40°
故答案为:40.
【点睛】
此题主要考查了平行线的性质、对顶角的性质,正确得出∠3=∠2是解题关键.
12..
【解析】
【分析】
利用平行线的性质和三角形的内角和即可求出.
【详解】
延长ED交AC于F,
∵AB∥DE,
∴∠3=∠BAC=m°,∠1=180°?∠3=180°?m°,
∠2=180°?∠CDE=180°?n°,
故∠C=∠3?∠2=m°?180°+n°=m°+n°?180°.
故答案为:m°+n°?180°.
【点睛】
本题主要考查了平行线的性质以及三角形外角性质的运用,解题时注意:此题要构造辅助线,运用三角形的一个外角等于和它不相邻的两个内角和.
13.45°.
【解析】
【分析】
首先过点B作BD∥l,由直线l∥m,可得BD∥l∥m,由两直线平行,内错角相等,可得出∠2=∠3,∠1=∠4,故∠1+∠2=∠3+∠4,由此即可得出结论.
【详解】
解:过点B作BD∥l,
∵直线l∥m,
∴BD∥l∥m,
∴∠4=∠1,∠2=∠3,
∴∠1+∠2=∠3+∠4=∠ABC,
∵∠ABC=45°,
∴∠1+∠2=45°.
故答案为:45°.
【点睛】
此题考查了平行线的性质.解题时注意辅助线的作法,注意掌握两直线平行,内错角相等定理的应用.
14.110°
【解析】
【分析】
由∠1,∠2互补及邻补角互补可得出∠2=∠5,利用“同位角相等,两直线平行”可得出l1∥l2,利用“两直线平行,同位角相等”可得出∠3=∠6,再结合∠3的度数及∠4,∠6互补可求出∠4的度数.
【详解】
∵∠1=80°,∠2=100°,∴∠1+∠2=180°.
∵∠1+∠5=180°,∴∠2=∠5,∴l1∥l2,∴∠3=∠6.
∵∠4+∠6=180°,∠3=∠6=70°,∴∠4=110°.
故答案为:110°.
【点睛】
本题考查了平行线的判定与性质,利用平行线的性质,求出∠6的度数是解题的关键.
15.(1)∠1=∠2,证明见解析;(2)∠1+∠2=180°,证明见解析;(3)一个角的两边与另一个角的两边分别平行,这两个角相等或互补;(4)这两个角分别是30°,30°或70°,110°.
【解析】
【分析】
(1)根据两直线平行,内错角相等,可求出∠1=∠2; (2)根据两直线平行,内错角相等及同旁内角互补可求出∠1+∠2=180°; (3)由(1)(2)可得出结论;
(4)由(3)可列出方程,求出角的度数.
【详解】
解:(1)AB∥EF,BC∥DE,∠1与∠2的关系是:∠1=∠2 证明:∵AB∥EF ∴∠1=∠BCE ∵BC∥DE ∴∠2=∠BCE ∴∠1=∠2. (2)AB∥EF,BC∥DE.∠1与∠2的关系是:∠1+∠2=180°. 证明:∵AB∥EF ∴∠1=∠BCE ∵BC∥DE ∴∠2+∠BCE=180° ∴∠1+∠2=180°. (3)经过上述证明,我们可以得到一个真命题:如果一个角的两边与另一个角的两边分别平行,那么这两个角相等或互补. (4)解:设其中一个角为x°,列方程得x=2x-30或x+2x-30=180, 故x=30或x=70, 所以2x-30=30或110, 答:这两个角分别是30°,30°或70°,110°.
【点睛】
本题考查平行线的性质,解题的关键是注意数形结合思想的应用,注意两直线平行,内错角相等与两直线平行,同旁内角互补定理的应用.
16.(1)见解析;(2)见解析;(3)见解析.
【解析】
【分析】
(1)根据平行线的性质解答即可;
(2)根据平行线的性质解答即可;
(3)根据平行线的性质解答即可.
【详解】
(1)∵ AB∥CF,(已知)
∴ ∠1=∠ F ,( 两直线平行,内错角相等 )
∠A+∠ ACF =180°. ( 两直线平行,同旁内角互补)
故答案为:F;两直线平行,内错角相等;ACF ;两直线平行,同旁内角互补
(2)∵ ∠A=∠ 1 ,( 已知 )
∴ AC∥EF;( 同位角相等,两直线平行 )
故答案为:1;同位角相等,两直线平行
(3)∵ ∠2=∠ ACB ,( 已知 )
∴ AC ∥ EF ;( 内错角相等,两直线平行 )
故答案为:ACB;AC;EF;内错角相等,两直线平行
【点睛】
本题考查的是平行线的性质及判定,掌握平行线的性质及判定定理是关键.
17.同位角相等 两直线平行
【解析】
【分析】
由题意利用平行线性质以及平行线判定定理和角平分线的定义进行分析即可.
【详解】
解:,
又,
(同位角相等 两直线平行)
(两直线平行 同旁内角互补)
,
平分,
(角平分线的定义)
,
(两直线平行内错角相等)
【点睛】
本题考查平行线的性质和判定、角平分线的定义,能熟练地运用定理进行推理是解此题的关键.
18.32°
【解析】
【分析】
根据两直线平行,内错角相等求出∠DCB的度数,从而求得∠DCE的度数,再根据两直线平行,内错角相等求得∠AEC的度数,根据两直线平行同旁内角互补即可求解.
【详解】
解:∵AB∥CD,
∴∠B=∠DCB, ∠DCE=∠AEC, ∠AED+∠D=180°
∵∠B=44°,
∴∠DCB=44°
∵∠BCE=30°,
∴∠DCE=∠DCB+∠BCE=44°+30°=74°,
∴∠AEC=∠DCE=74°,
∵EC为∠AED的角平分线,
∴∠AED=2∠AEC=2×74°=148°,
∴∠D=32°.
【点睛】
本题主要考查平行线的性质,由“平行”到“角的数量关系”的转换思想是解答此题的重要途径.
学校:___________姓名:___________班级:___________考号:___________
一、单选题
1.如图,已知∠1=∠2,∠3=65°,那么∠4的度数是( )
A.55° B.95° C.115° D.145°
2.在、两座工厂之间要修建一条笔直的公路,从地测得地的走向是南偏东,现、两地要同时开工,若干天后,公路准确对接,则地所修公路的走向应该是( )
A.北偏西 B.南偏东 C.西偏北 D.北偏西
3.如图,直线a∥b,直线AB⊥AC,若∠1=50°,则∠2的度数为
A.50° B.45° C.30° D.40°
4.如图,已知直线a、b被直线c所截,a∥b,∠1=130°,则 ∠2=( )
A.130° B.50° C.40° D.60°
5.已知直线m∥n,将一块含30°角的直角三角板ABC按如图方式放置(∠ABC=30°),其中A,B两点分别落在直线m,n上,若∠1=20°,则∠2的度数为( )
A.20° B.30° C.45° D.50°
6.如图,已知直线,,,则等于( )
A. B. C. D.
7.如图,AB∥CD,则根据图中标注的角,下列关系中成立的是 ( )
A.∠1=∠3 B.∠2+∠3=180° C.∠2+∠4<180° D.∠3+∠5=180°
8.如图,OC是∠AOB的角平分线,l//OB,若∠1=52°,则∠2的度数为( )
A.52° B.54° C.64° D.69°
二、填空题
9.如图,已知直线,则的度数为______.
10.如图:若,,则__________.
11.如图,a∥b,若∠1=40°,则∠2=_____度.
12.如图,已知,则___________°.
13.如图,直线l∥m,将含有45°角的三角板ABC的直角顶点C放在直线m上,则∠1+∠2的度数为_____.
14.如图,已知∠1=80°,∠2=100°,∠3=70°,则∠4=_____.
三、解答题
15.已知一角的两边与另一个角的两边平行,分别结合下图,试探索这两个角之间的关系,并证明你的结论.
(1)如图(1)AB∥EF,BC∥DE,∠1与∠2的关系是:____________ .
(2)如图(2)AB∥EF,BC∥DE, ∠1与∠2的关系是:____________
(3)经过上述证明,我们可以得到一个真命题:如果____ _____,那么____________.
(4)若两个角的两边互相平行,且一个角比另一个角的2倍少30°,则这两个角分别是多少度?
16.如图,在下列解答中,填空或填写适当的理由:
(1),(已知)
______________.(___________________________________________)
________________(______________________________________)
(2)_______,(已知)
;(___________________________________)
(3)_______________,(已知)
__________________________.(_______________________________)
17.如图,,平分.若,求的度数。根据提示将解题过程补充完整.
解:(平角),
又(已知),
,(_________)
(_________),(两直线平行,同旁内角互补)
,
(_________)
平分,
(_________).(角平分线的定义)
,
(_________)(两直线平行,内错角相等)
18.如图,已知和,在边上,且,为的角平分线,若,,求的度数.
参考答案
1.C
【解析】
【分析】
根据平行线的判定得出a∥b,根据平行线的性质得出∠4+∠5=180°,求出∠5即可.
【详解】
解:
∠1=∠2,
∴a∥b,
∴∠4+∠5=180°
∠3=65°
∴∠5=∠3=65°
∴∠4=180°-65°=115°
故选C.
【点睛】
本题考查平行线的性质和判定,能灵活运用定理进行分析推理是解此题的关键.
2.A
【解析】
如图,连接AB,
由题意得:∠CAB=52°,
∵DB∥AC,
∴∠CAB=∠ABD=52°,
∴B地所修公路走向应该是北偏西52°.
故选A.
点睛:本题结合方位角、平行线的性质解题.
3.D
【解析】
【分析】
根据两直线平行,内错角相等可得∠3=∠1,根据垂直的定义和余角的定义计算得到∠2.
【详解】
解:∵直线a∥b,∠1=50°, ∴∠1=∠3=50°, ∵AB⊥AC, ∴∠2+∠3=90°. ∴∠2=40°. 故选:D.
【点睛】
本题考查平行线的性质以及垂直的定义,属于中考常考题.
4.B
【解析】
【分析】
先根据邻补角的定义求出∠3,再利用两直线平行,同位角相等解答即可.
【详解】
解:如图
∵∠1=30°, ∴∠3=180°?∠1=180°?130°=50°, ∵a//b, ∴∠2=∠3=50°, 故答案为50°.
【点睛】
本题考查了平行线的性质,邻补角的定义,熟记性质是解题的关键.
5.D
【解析】
【分析】
根据两直线平行,内错角相等计算即可.
【详解】
因为m∥n,所以∠2=∠1+30°,所以∠2=30°+20°=50°,故选D.
【点睛】
本题主要考查平行线的性质,清楚两直线平行,内错角相等是解答本题的关键.
6.A
【解析】
【分析】
先过点C作CD∥a,根据平行于同一直线的两条直线互相平行,即可得CD∥a∥b,根据两直线平行,内错角相等,即可求得∠ACB的度数.
【详解】
如图,过点C作CD∥a.
∵a∥b,∴CD∥a∥b,∴∠ACD=∠1=40°,∠BCD=∠2=60°,∴∠ACB=∠ACD+∠BCD=100°.
故选A.
【点睛】
本题考查了平行线的性质.正确作出辅助线是解答本题的关键.
7.D
【解析】
试题分析:根据平行线的性质对各选项分析判断利用排除法求解:
A、∵OC与OD不平行,∴∠1=∠3不成立,故本选项错误;
B、∵OC与OD不平行,∴∠2+∠3=180°不成立,故本选项错误;
C、∵AB∥CD,∴∠2+∠4=180°,故本选项错误;
D、∵AB∥CD,∴∠3+∠5=180°,故本选项正确.
故选D.
考点:平行线的性质.
8.C
【解析】
【分析】
先根据两直线平行,同旁内角互补求出∠AOB=128°,再根据角平分线的定义得到∠BOC=64°,继而根据平行线的性质即可求得答案.
【详解】
∵l//OB,
∴∠1+∠AOB=180°,
∴∠AOB=128°,
∵OC平分∠AOB,
∴∠BOC=64°,
又∵l//OB,
∴∠2=∠BOC=64°,
故选C.
【点睛】
本题考查了平行线的性质,角平分线的定义,熟练掌握平行线的性质是解本题的关键.
9.50°
【解析】
【分析】
如图所示(见解析),由可得,,又因和角互补,则,从而可得.
【详解】
画图如下所示:
(两直线平行,同位角相等)
又和角互补
.
故的度数为.
【点睛】
本题考查了角互补的定义、平行线的性质,属于基础题型.平行线的性质有:(1)两直线平行,同位角相等;(2)两直线平行,内错角相等;(3)两直线平行,同旁内角互补.
10.
【解析】
【分析】
根据平行线的性质,得∠1的同位角是45°,再根据邻补角的定义,得:∠2=180°-45°=135°.
【详解】
∵∥,,
∴∠1的同位角是,
∴∠2.
故答案为:
【点睛】
考查平行线的性质,掌握两直线平行,同位角相等是解题的关键.
11.40
【解析】
【分析】
直接利用平行线的性质结合对顶角的性质分析得出答案.
【详解】
解:
∵∠1=40°,
∴∠1=∠3=40°
∵a∥b,
∴∠2=∠3=40°
故答案为:40.
【点睛】
此题主要考查了平行线的性质、对顶角的性质,正确得出∠3=∠2是解题关键.
12..
【解析】
【分析】
利用平行线的性质和三角形的内角和即可求出.
【详解】
延长ED交AC于F,
∵AB∥DE,
∴∠3=∠BAC=m°,∠1=180°?∠3=180°?m°,
∠2=180°?∠CDE=180°?n°,
故∠C=∠3?∠2=m°?180°+n°=m°+n°?180°.
故答案为:m°+n°?180°.
【点睛】
本题主要考查了平行线的性质以及三角形外角性质的运用,解题时注意:此题要构造辅助线,运用三角形的一个外角等于和它不相邻的两个内角和.
13.45°.
【解析】
【分析】
首先过点B作BD∥l,由直线l∥m,可得BD∥l∥m,由两直线平行,内错角相等,可得出∠2=∠3,∠1=∠4,故∠1+∠2=∠3+∠4,由此即可得出结论.
【详解】
解:过点B作BD∥l,
∵直线l∥m,
∴BD∥l∥m,
∴∠4=∠1,∠2=∠3,
∴∠1+∠2=∠3+∠4=∠ABC,
∵∠ABC=45°,
∴∠1+∠2=45°.
故答案为:45°.
【点睛】
此题考查了平行线的性质.解题时注意辅助线的作法,注意掌握两直线平行,内错角相等定理的应用.
14.110°
【解析】
【分析】
由∠1,∠2互补及邻补角互补可得出∠2=∠5,利用“同位角相等,两直线平行”可得出l1∥l2,利用“两直线平行,同位角相等”可得出∠3=∠6,再结合∠3的度数及∠4,∠6互补可求出∠4的度数.
【详解】
∵∠1=80°,∠2=100°,∴∠1+∠2=180°.
∵∠1+∠5=180°,∴∠2=∠5,∴l1∥l2,∴∠3=∠6.
∵∠4+∠6=180°,∠3=∠6=70°,∴∠4=110°.
故答案为:110°.
【点睛】
本题考查了平行线的判定与性质,利用平行线的性质,求出∠6的度数是解题的关键.
15.(1)∠1=∠2,证明见解析;(2)∠1+∠2=180°,证明见解析;(3)一个角的两边与另一个角的两边分别平行,这两个角相等或互补;(4)这两个角分别是30°,30°或70°,110°.
【解析】
【分析】
(1)根据两直线平行,内错角相等,可求出∠1=∠2; (2)根据两直线平行,内错角相等及同旁内角互补可求出∠1+∠2=180°; (3)由(1)(2)可得出结论;
(4)由(3)可列出方程,求出角的度数.
【详解】
解:(1)AB∥EF,BC∥DE,∠1与∠2的关系是:∠1=∠2 证明:∵AB∥EF ∴∠1=∠BCE ∵BC∥DE ∴∠2=∠BCE ∴∠1=∠2. (2)AB∥EF,BC∥DE.∠1与∠2的关系是:∠1+∠2=180°. 证明:∵AB∥EF ∴∠1=∠BCE ∵BC∥DE ∴∠2+∠BCE=180° ∴∠1+∠2=180°. (3)经过上述证明,我们可以得到一个真命题:如果一个角的两边与另一个角的两边分别平行,那么这两个角相等或互补. (4)解:设其中一个角为x°,列方程得x=2x-30或x+2x-30=180, 故x=30或x=70, 所以2x-30=30或110, 答:这两个角分别是30°,30°或70°,110°.
【点睛】
本题考查平行线的性质,解题的关键是注意数形结合思想的应用,注意两直线平行,内错角相等与两直线平行,同旁内角互补定理的应用.
16.(1)见解析;(2)见解析;(3)见解析.
【解析】
【分析】
(1)根据平行线的性质解答即可;
(2)根据平行线的性质解答即可;
(3)根据平行线的性质解答即可.
【详解】
(1)∵ AB∥CF,(已知)
∴ ∠1=∠ F ,( 两直线平行,内错角相等 )
∠A+∠ ACF =180°. ( 两直线平行,同旁内角互补)
故答案为:F;两直线平行,内错角相等;ACF ;两直线平行,同旁内角互补
(2)∵ ∠A=∠ 1 ,( 已知 )
∴ AC∥EF;( 同位角相等,两直线平行 )
故答案为:1;同位角相等,两直线平行
(3)∵ ∠2=∠ ACB ,( 已知 )
∴ AC ∥ EF ;( 内错角相等,两直线平行 )
故答案为:ACB;AC;EF;内错角相等,两直线平行
【点睛】
本题考查的是平行线的性质及判定,掌握平行线的性质及判定定理是关键.
17.同位角相等 两直线平行
【解析】
【分析】
由题意利用平行线性质以及平行线判定定理和角平分线的定义进行分析即可.
【详解】
解:,
又,
(同位角相等 两直线平行)
(两直线平行 同旁内角互补)
,
平分,
(角平分线的定义)
,
(两直线平行内错角相等)
【点睛】
本题考查平行线的性质和判定、角平分线的定义,能熟练地运用定理进行推理是解此题的关键.
18.32°
【解析】
【分析】
根据两直线平行,内错角相等求出∠DCB的度数,从而求得∠DCE的度数,再根据两直线平行,内错角相等求得∠AEC的度数,根据两直线平行同旁内角互补即可求解.
【详解】
解:∵AB∥CD,
∴∠B=∠DCB, ∠DCE=∠AEC, ∠AED+∠D=180°
∵∠B=44°,
∴∠DCB=44°
∵∠BCE=30°,
∴∠DCE=∠DCB+∠BCE=44°+30°=74°,
∴∠AEC=∠DCE=74°,
∵EC为∠AED的角平分线,
∴∠AED=2∠AEC=2×74°=148°,
∴∠D=32°.
【点睛】
本题主要考查平行线的性质,由“平行”到“角的数量关系”的转换思想是解答此题的重要途径.
同课章节目录
- 第一章 整式的乘除
- 1 同底数幂的乘法
- 2 幂的乘方与积的乘方
- 3 同底数幂的除法
- 4 整式的乘法
- 5 平方差公式
- 6 完全平方公式
- 7 整式的除法
- 第二章 相交线与平行线
- 1 两条直线的位置关系
- 2 探索直线平行的条件
- 3 平行线的性质
- 4 用尺规作角
- 第三章 变量之间的关系
- 1 用表格表示的变量间关系
- 2 用关系式表示的变量间关系
- 3 用图象表示的变量间关系
- 第四章 三角形
- 1 认识三角形
- 2 图形的全等
- 3 探索三角形全等的条件
- 4 用尺规作三角形
- 5 利用三角形全等测距离
- 第五章 生活中的轴对称
- 1 轴对称现象
- 2 探索轴对称的性质
- 3 简单的轴对称图形
- 4 利用轴对称进行设计
- 第六章 概率初步
- 1 感受可能性
- 2 频率的稳定性
- 3 等可能事件的概率
