北师大版七年级数学下册同步精练专题 2.3平行线的性质同步训练(含解析)
文档属性
| 名称 | 北师大版七年级数学下册同步精练专题 2.3平行线的性质同步训练(含解析) |  | |
| 格式 | zip | ||
| 文件大小 | 289.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-02-13 11:26:50 | ||
图片预览



文档简介
2.3平行线的性质同步训练
学校:___________姓名:___________班级:___________考号:___________
一、单选题
1.如图,直线AB、CD相交于点E,EF⊥AB于E,若∠CEF=65°,则∠DEB的度数为( )
A.155° B.135° C.35° D.25°
2.如果两个角的两边分别平行,且其中一个角比另一个角的4倍少,那么这两个角是( )
A.和 B.都是
C.和或都是 D.以上都不对
3.如图,如果,那么之间的关系是( )
A. B.
C. D.
4.直尺与三角尺按如图所示的方式叠放在一起,在图中所标记的角中,与∠1互余的角有几个
A.2个 B.3个 C.4个 D.6个
5.如图,点A在直线BG上,AD∥BC,AE平分∠GAD, 若∠CBA=80°,则∠GAE= ( )
A.60° B.50° C.40° D.30°
6.如图,AB∥CD,点E在CA的延长线上.若∠BAE=40°,则∠ACD的大小为( )
A.150° B.140° C.130° D.120°
7.如图,a∥b,将三角尺的直角顶点放在直线a上,若∠1=40°,则∠2=( )
A.30° B.40° C.50° D.60°
8.如图,已知,小明把三角板的直角顶点放在直线b上若,则的度数为
A. B. C. D.
二、填空题
9.如图,直线AD∥BC,若∠1=42°,∠BAC=78°,则∠2的度数为______.
10.如图,∠COB=2∠AOC,OD平分∠AOB,且∠COD=19°,则∠AOB=_____度.
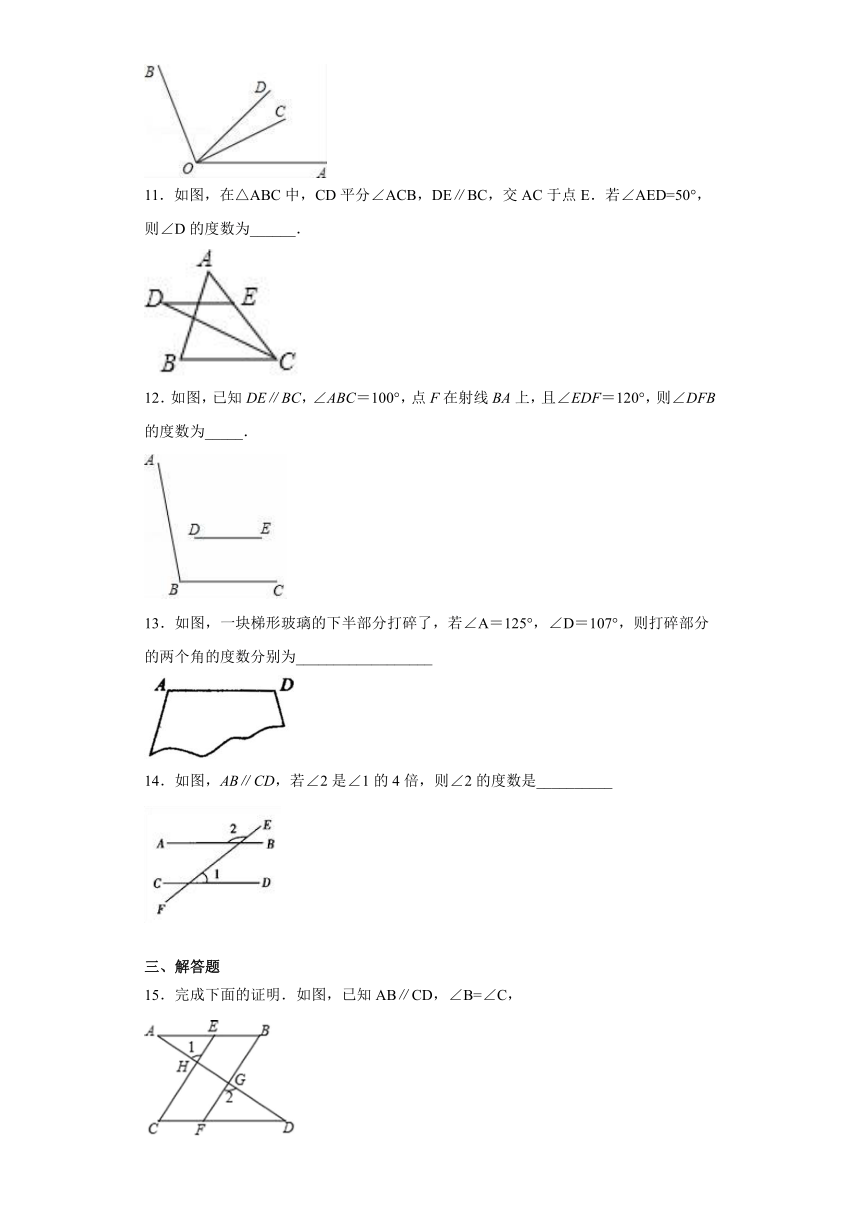
11.如图,在△ABC中,CD平分∠ACB,DE∥BC,交AC于点E.若∠AED=50°,则∠D的度数为______.
12.如图,已知DE∥BC,∠ABC=100°,点F在射线BA上,且∠EDF=120°,则∠DFB的度数为_____.
13.如图,一块梯形玻璃的下半部分打碎了,若∠A=125°,∠D=107°,则打碎部分的两个角的度数分别为__________________
14.如图,AB∥CD,若∠2是∠1的4倍,则∠2的度数是__________
三、解答题
15.完成下面的证明.如图,已知AB∥CD,∠B=∠C,
求证:∠1=∠2.
证明:∵AB∥CD(已知)
∴∠B= ( ).
∵∠B=∠C(已知)
∴∠BFD=∠C(等量代换)
∴EC∥ ( )
∴∠2= (两直线平行,同位角相等)
∵∠1= ( )
∴∠1=∠2(等量代换).
16.如图,已知AB∥CD,被直线EF所截交AB、CD于点M、N,MP平分∠EMB,NQ平分∠MND,证明:MP∥NQ.
17.如图(1),AB∥CD,猜想∠BPD与∠B、∠D的关系,说出理由.
解:猜想∠BPD+∠B+∠D=360°
理由:过点P作EF∥AB,
∴∠B+∠BPE=180°(两直线平行,同旁内角互补)
∵AB∥CD,EF∥AB,
∴EF∥CD,(如果两条直线都和第三条直线平行,那么这两条直线也互相平行.)
∴∠EPD+∠D=180°(两直线平行,同旁内角互补)
∴∠B+∠BPE+∠EPD+∠D=360°
∴∠B+∠BPD+∠D=360°
(1)依照上面的解题方法,观察图(2),已知AB∥CD,猜想图中的∠BPD与∠B、∠D的关系,并说明理由.
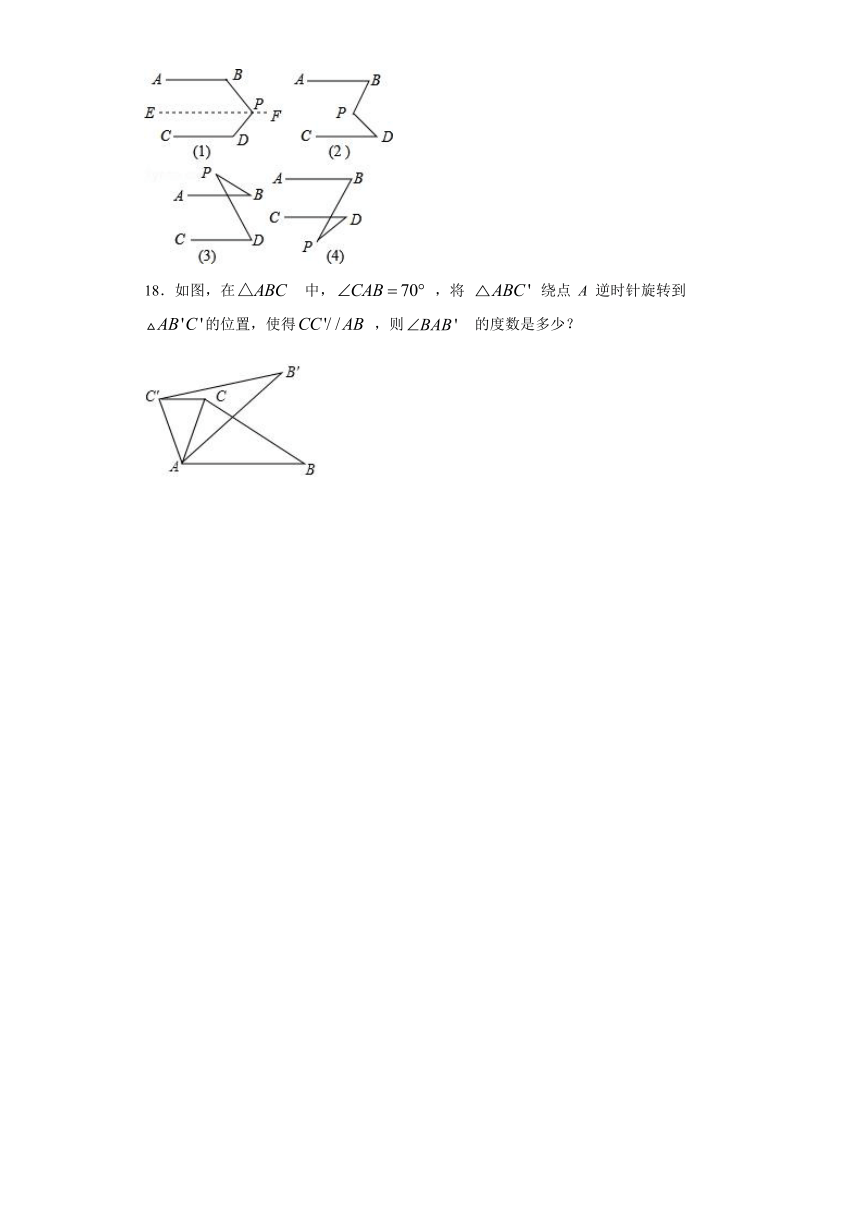
(2)观察图(3)和(4),已知AB∥CD,猜想图中的∠BPD与∠B、∠D的关系,不需要说明理由.
18.如图,在 中, ,将 绕点 A 逆时针旋转到的位置,使得 ,则 的度数是多少?
参考答案
1.D
【解析】
【分析】
直接利用垂直的定义结合互余的性质、对顶角的性质得出答案.
【详解】
于,,
,
则.
故选:.
【点睛】
此题主要考查了垂线以及对顶角,正确得出的度数是解题关键.
2.C
【解析】
设一个角为?x?度,则另一个角为(4?x-30)度, ∵如果两个角的两边分别平行,那么这两个角相等或互补 ∴4x-30=x?或4x-30+x=180, 解得:x=10或?x=42, 当?x=42时,4x-30=138, 即这两个角是10°、10°或42°、138°, 故选C.
3.D
【解析】
【分析】
根据两直线平行,同旁内角互补以及内错角相等即可解答,此题在解答过程中,需添加辅助线.
【详解】
过点E作EF∥AB,则EF∥CD.
∵EF∥AB∥CD,
∴∠α+∠AEF=180°,∠FED=∠γ,
∴∠α+∠β=180°+∠γ,
即∠α+∠β?∠γ=180°.
故选D.
【点睛】
此题考查平行线的性质,解题关键在于作辅助线.
4.B
【解析】
分析:注意到∠1与∠2互余,并且直尺的两边互相平行,根据平行线的性质,有∠2=∠3=∠4,所以,与∠1互余的角有∠2,∠3,∠4;一共3个.故选B.
5.B
【解析】
【分析】
先求出∠BAD=∠CBA=80°,2∠GAE+∠BAD=180°即可求出∠GAE.
【详解】
∵AD∥BC,
∴∠BAD=∠CBA=80°,
∵AE平分∠GAD,
则∠GAE=∠GAD,
∴2∠GAE+∠BAD=180°,
得∠GAE=50°.
【点睛】
此题主要考察平行线的性质和角的计算.
6.B
【解析】
试题分析:如图,延长DC到F,则
∵AB∥CD,∠BAE=40°,∴∠ECF=∠BAE=40°.
∴∠ACD=180°-∠ECF=140°.
故选B.
考点:1.平行线的性质;2.平角性质.
7.C
【解析】
【分析】
先求出∠3的度数,根据平行线的性质得出∠2=∠3,代入求出即可.
【详解】
解:∵∠1=40°, ∴∠3=90°-40=50°, ∵直线a∥直线b, ∴∠2=∠3=50°, 故选:C.
【点睛】
本题考查平行线的性质的应用,注意:两直线平行,内错角相等,题目比较典型,难度适中.
8.C
【解析】
【分析】
由直角三角板的性质可知,再根据平行线的性质即可得出结论.
【详解】
解:,
,
,
.
故选:C.
【点睛】
本题考查的是平行线的性质,用到的知识点为:两直线平行,同位角相等.
9.60°
【解析】
【分析】
依据三角形内角和定理,即可得到∠ABC=60°,再根据AD∥BC,即可得出∠2=∠ABC=60°.
【详解】
∵∠1=42°,∠BAC=78°, ∴∠ABC=60°, 又∵AD∥BC, ∴∠2=∠ABC=60°, 故答案是:60°.
【点睛】
考查了平行线的性质,解题时注意:两直线平行,内错角相等.
10.114.
【解析】
【分析】
本题是角平分线的应用,同时也可以借助方程来解决.
【详解】
因为∠COB=2∠AOC,
所以设∠AOC=x,
则∠COB=2x,
所以∠AOB=3x,
因为OD平分∠AOB,
所以∠BOD=∠AOD=1.5x,
所以∠COD=∠AOD-∠AOC=1.5x-x=19°,
所以x=38°,
所以∠AOB=3x=3×38°=114°.
故答案为114.
【点睛】
此题主要考查了角平分线的性质.方程思想在角的大小求解中经常用到,灵活的应用方程思想求解可以事半功倍.
11.25°
【解析】
【分析】
根据平行线的性质求得∠ACB度数,然后根据角平分线的定义求得∠DCB的度数,然后利用两直线平行,内错角相等即可求解.
【详解】
解:∵DE∥BC,∠AED=50°,
∴∠ACB=∠AED=50°,
∵CD平分∠ACB,
∴∠BCD=∠ACB=25°,
∵DE∥BC,
∴∠D=∠BCD=25°,
故答案为:25°.
【点睛】
本题重点考查了平行线的性质及角平分线的定义,是一道较为简单的题目.
12.20°或140°.
【解析】
【分析】
根据平行线的性质,分两种情况分析:当F在直线DE的上侧或F在直线DE的下侧.
【详解】
如图,当F在直线DE的下侧,作FH∥BC,
因为,DE∥BC,
所以,DE∥BC∥FH
所以,∠ABC+∠D+∠BFD=180°×2=360°,
所以,∠BFD=360°-∠ABC-∠D=140°
.
当F在直线DE的上侧,作FH∥BC,
因为,DE∥BC,
所以,DE∥BC∥FH
所以,∠ABC=∠BFH=100°,∠FDE=∠DFH=120°
所以,∠BFD=∠DFH-∠BFH=120°-100°=20°,
故答案为:20°或140°
【点睛】
平行线的性质和判定的灵活运用.
13.55°,73°
【解析】
【分析】
因为在梯形ABCD中,AD∥BC,所以∠A+∠B=180°,∠D+∠C=180°(两直线平行,同旁内角互补);
则可求得下半部分的两个角∠B和∠C的度数.
【详解】
将原图补全,如图,
.
∵AD∥BC,
∴∠D+∠C=180°,∠A+∠B=180°,
∴∠B=180°-∠A=180°-125°=55°,∠C=180°-∠D=180°-107°=73°,
【点睛】
此题考查了梯形的两底平行与平行线的性质.两直线平行,同旁内角互补.
14.144°
【解析】
如图所示:
∵AB∥CD, ∴∠1+∠BMN=180°, ∵∠2=∠BMN, ∴∠1+∠2=180°, ∵∠2是∠1的4倍, ∴5∠1=180°, ∴∠1=36°, ∴∠2=144°.
故答案是:144°.
15.∠BFD,两直线平行,内错角相等; BF(或FG),同位角相等,两直线平行;∠CHD(或∠CHG);∠CHD(或∠CHG),对顶角相等;
【解析】
【分析】
根据题目过程,结合平行的性质与判定即可完成.
【详解】
证明:∵AB∥CD(已知)
∴∠B= ∠BFD ( 两直线平行,内错角相等 ).
∵∠B=∠C(已知)
∴∠BFD=∠C(等量代换)
∴EC∥ BF(或FG) ( 同位角相等,两直线平行 )
∴∠2= ∠CHD(或∠CHG) (两直线平行,同位角相等)
∵∠1= ∠CHD(或∠CHG) ( 对顶角相等 )
∴∠1=∠2(等量代换).
【点睛】
本题考查平行线的性质和判定,难度较低,熟练掌握平行线的相关性质定理是解题关键.
16.详见解析
【解析】
【分析】
由AB∥CD,根据平行线的性质得∠EMB=∠MND,再根据角平分线的定义得到∠EMP=∠EMB,∠MNQ=∠MND,则∠EMP=∠MNQ,然后根据平行线的判定即可得到MP∥NQ.
【详解】
证明:∵AB∥CD,
∴∠EMB=∠MND,
∵N,MP平分∠EMB,NQ平分∠MND,
∴∠EMP=∠EMB,∠MNQ=∠MND,
∴∠EMP=∠MNQ,
∴MP∥NQ.
【点睛】
本题考查了平行线的判定与性质:两直线平行,同位角相等;同位角相等,两直线平行.
17.见解析
【解析】
【分析】
(1)首先过点P作PE∥AB,由AB∥CD,可得PE∥AB∥CD,根据两直线平行,内错角相等,即可得∠1=∠B,∠2=∠D,则可求得∠BPD=∠B+∠D.
(2)由AB∥CD,根据两直线平行,内错角相等与三角形外角的性质,即可求得∠BPD与∠B、∠D的关系.
【详解】
解:(1)∠BPD=∠B+∠D.
理由:如图2,过点P作PE∥AB,
∵AB∥CD,
∴PE∥AB∥CD,
∴∠1=∠B,∠2=∠D,
∴∠BPD=∠1+∠2=∠B+∠D;
(2)如图(3):∠BPD=∠D﹣∠B.
理由:∵AB∥CD,
∴∠1=∠D,
∵∠1=∠B+∠P,
∴∠D=∠B+∠P,
即∠BPD=∠D﹣∠B;
如图(4):∠BPD=∠B﹣∠D.
理由:∵AB∥CD,
∴∠1=∠B,
∵∠1=∠D+∠P,
∴∠B=∠D+∠P,
即∠BPD=∠B﹣∠D.
18.40°
【解析】
【分析】
根据旋转的性质得AC′=AC,∠B′AB=∠C′AC,再根据等腰三角形的性质得∠AC′C=∠ACC′,然后根据平行线的性质由CC′∥AB得∠ACC′=∠CAB=70°,则∠AC′C=∠ACC′=70°,再根据三角形内角和计算出∠CAC′=40°,所以∠B′AB=40°.
【详解】
解:∵△ABC绕点A逆时针旋转到△AB′C′的位置,
∴AC′=AC,∠B′AB=∠C′AC,
∴∠AC′C=∠ACC′,
∵CC′∥AB,
∴∠ACC′=∠CAB=70°,
∴∠AC′C=∠ACC′=70°,
∴∠CAC′=180°-2×70°=40°,
∴∠B′AB=40°.
【点睛】
本题考查了旋转的性质:旋转前后两图形全等;对应点到旋转中心的距离相等;对应点与旋转中心的连线段的夹角等于旋转角.也考查了平行线的性质.
学校:___________姓名:___________班级:___________考号:___________
一、单选题
1.如图,直线AB、CD相交于点E,EF⊥AB于E,若∠CEF=65°,则∠DEB的度数为( )
A.155° B.135° C.35° D.25°
2.如果两个角的两边分别平行,且其中一个角比另一个角的4倍少,那么这两个角是( )
A.和 B.都是
C.和或都是 D.以上都不对
3.如图,如果,那么之间的关系是( )
A. B.
C. D.
4.直尺与三角尺按如图所示的方式叠放在一起,在图中所标记的角中,与∠1互余的角有几个
A.2个 B.3个 C.4个 D.6个
5.如图,点A在直线BG上,AD∥BC,AE平分∠GAD, 若∠CBA=80°,则∠GAE= ( )
A.60° B.50° C.40° D.30°
6.如图,AB∥CD,点E在CA的延长线上.若∠BAE=40°,则∠ACD的大小为( )
A.150° B.140° C.130° D.120°
7.如图,a∥b,将三角尺的直角顶点放在直线a上,若∠1=40°,则∠2=( )
A.30° B.40° C.50° D.60°
8.如图,已知,小明把三角板的直角顶点放在直线b上若,则的度数为
A. B. C. D.
二、填空题
9.如图,直线AD∥BC,若∠1=42°,∠BAC=78°,则∠2的度数为______.
10.如图,∠COB=2∠AOC,OD平分∠AOB,且∠COD=19°,则∠AOB=_____度.
11.如图,在△ABC中,CD平分∠ACB,DE∥BC,交AC于点E.若∠AED=50°,则∠D的度数为______.
12.如图,已知DE∥BC,∠ABC=100°,点F在射线BA上,且∠EDF=120°,则∠DFB的度数为_____.
13.如图,一块梯形玻璃的下半部分打碎了,若∠A=125°,∠D=107°,则打碎部分的两个角的度数分别为__________________
14.如图,AB∥CD,若∠2是∠1的4倍,则∠2的度数是__________
三、解答题
15.完成下面的证明.如图,已知AB∥CD,∠B=∠C,
求证:∠1=∠2.
证明:∵AB∥CD(已知)
∴∠B= ( ).
∵∠B=∠C(已知)
∴∠BFD=∠C(等量代换)
∴EC∥ ( )
∴∠2= (两直线平行,同位角相等)
∵∠1= ( )
∴∠1=∠2(等量代换).
16.如图,已知AB∥CD,被直线EF所截交AB、CD于点M、N,MP平分∠EMB,NQ平分∠MND,证明:MP∥NQ.
17.如图(1),AB∥CD,猜想∠BPD与∠B、∠D的关系,说出理由.
解:猜想∠BPD+∠B+∠D=360°
理由:过点P作EF∥AB,
∴∠B+∠BPE=180°(两直线平行,同旁内角互补)
∵AB∥CD,EF∥AB,
∴EF∥CD,(如果两条直线都和第三条直线平行,那么这两条直线也互相平行.)
∴∠EPD+∠D=180°(两直线平行,同旁内角互补)
∴∠B+∠BPE+∠EPD+∠D=360°
∴∠B+∠BPD+∠D=360°
(1)依照上面的解题方法,观察图(2),已知AB∥CD,猜想图中的∠BPD与∠B、∠D的关系,并说明理由.
(2)观察图(3)和(4),已知AB∥CD,猜想图中的∠BPD与∠B、∠D的关系,不需要说明理由.
18.如图,在 中, ,将 绕点 A 逆时针旋转到的位置,使得 ,则 的度数是多少?
参考答案
1.D
【解析】
【分析】
直接利用垂直的定义结合互余的性质、对顶角的性质得出答案.
【详解】
于,,
,
则.
故选:.
【点睛】
此题主要考查了垂线以及对顶角,正确得出的度数是解题关键.
2.C
【解析】
设一个角为?x?度,则另一个角为(4?x-30)度, ∵如果两个角的两边分别平行,那么这两个角相等或互补 ∴4x-30=x?或4x-30+x=180, 解得:x=10或?x=42, 当?x=42时,4x-30=138, 即这两个角是10°、10°或42°、138°, 故选C.
3.D
【解析】
【分析】
根据两直线平行,同旁内角互补以及内错角相等即可解答,此题在解答过程中,需添加辅助线.
【详解】
过点E作EF∥AB,则EF∥CD.
∵EF∥AB∥CD,
∴∠α+∠AEF=180°,∠FED=∠γ,
∴∠α+∠β=180°+∠γ,
即∠α+∠β?∠γ=180°.
故选D.
【点睛】
此题考查平行线的性质,解题关键在于作辅助线.
4.B
【解析】
分析:注意到∠1与∠2互余,并且直尺的两边互相平行,根据平行线的性质,有∠2=∠3=∠4,所以,与∠1互余的角有∠2,∠3,∠4;一共3个.故选B.
5.B
【解析】
【分析】
先求出∠BAD=∠CBA=80°,2∠GAE+∠BAD=180°即可求出∠GAE.
【详解】
∵AD∥BC,
∴∠BAD=∠CBA=80°,
∵AE平分∠GAD,
则∠GAE=∠GAD,
∴2∠GAE+∠BAD=180°,
得∠GAE=50°.
【点睛】
此题主要考察平行线的性质和角的计算.
6.B
【解析】
试题分析:如图,延长DC到F,则
∵AB∥CD,∠BAE=40°,∴∠ECF=∠BAE=40°.
∴∠ACD=180°-∠ECF=140°.
故选B.
考点:1.平行线的性质;2.平角性质.
7.C
【解析】
【分析】
先求出∠3的度数,根据平行线的性质得出∠2=∠3,代入求出即可.
【详解】
解:∵∠1=40°, ∴∠3=90°-40=50°, ∵直线a∥直线b, ∴∠2=∠3=50°, 故选:C.
【点睛】
本题考查平行线的性质的应用,注意:两直线平行,内错角相等,题目比较典型,难度适中.
8.C
【解析】
【分析】
由直角三角板的性质可知,再根据平行线的性质即可得出结论.
【详解】
解:,
,
,
.
故选:C.
【点睛】
本题考查的是平行线的性质,用到的知识点为:两直线平行,同位角相等.
9.60°
【解析】
【分析】
依据三角形内角和定理,即可得到∠ABC=60°,再根据AD∥BC,即可得出∠2=∠ABC=60°.
【详解】
∵∠1=42°,∠BAC=78°, ∴∠ABC=60°, 又∵AD∥BC, ∴∠2=∠ABC=60°, 故答案是:60°.
【点睛】
考查了平行线的性质,解题时注意:两直线平行,内错角相等.
10.114.
【解析】
【分析】
本题是角平分线的应用,同时也可以借助方程来解决.
【详解】
因为∠COB=2∠AOC,
所以设∠AOC=x,
则∠COB=2x,
所以∠AOB=3x,
因为OD平分∠AOB,
所以∠BOD=∠AOD=1.5x,
所以∠COD=∠AOD-∠AOC=1.5x-x=19°,
所以x=38°,
所以∠AOB=3x=3×38°=114°.
故答案为114.
【点睛】
此题主要考查了角平分线的性质.方程思想在角的大小求解中经常用到,灵活的应用方程思想求解可以事半功倍.
11.25°
【解析】
【分析】
根据平行线的性质求得∠ACB度数,然后根据角平分线的定义求得∠DCB的度数,然后利用两直线平行,内错角相等即可求解.
【详解】
解:∵DE∥BC,∠AED=50°,
∴∠ACB=∠AED=50°,
∵CD平分∠ACB,
∴∠BCD=∠ACB=25°,
∵DE∥BC,
∴∠D=∠BCD=25°,
故答案为:25°.
【点睛】
本题重点考查了平行线的性质及角平分线的定义,是一道较为简单的题目.
12.20°或140°.
【解析】
【分析】
根据平行线的性质,分两种情况分析:当F在直线DE的上侧或F在直线DE的下侧.
【详解】
如图,当F在直线DE的下侧,作FH∥BC,
因为,DE∥BC,
所以,DE∥BC∥FH
所以,∠ABC+∠D+∠BFD=180°×2=360°,
所以,∠BFD=360°-∠ABC-∠D=140°
.
当F在直线DE的上侧,作FH∥BC,
因为,DE∥BC,
所以,DE∥BC∥FH
所以,∠ABC=∠BFH=100°,∠FDE=∠DFH=120°
所以,∠BFD=∠DFH-∠BFH=120°-100°=20°,
故答案为:20°或140°
【点睛】
平行线的性质和判定的灵活运用.
13.55°,73°
【解析】
【分析】
因为在梯形ABCD中,AD∥BC,所以∠A+∠B=180°,∠D+∠C=180°(两直线平行,同旁内角互补);
则可求得下半部分的两个角∠B和∠C的度数.
【详解】
将原图补全,如图,
.
∵AD∥BC,
∴∠D+∠C=180°,∠A+∠B=180°,
∴∠B=180°-∠A=180°-125°=55°,∠C=180°-∠D=180°-107°=73°,
【点睛】
此题考查了梯形的两底平行与平行线的性质.两直线平行,同旁内角互补.
14.144°
【解析】
如图所示:
∵AB∥CD, ∴∠1+∠BMN=180°, ∵∠2=∠BMN, ∴∠1+∠2=180°, ∵∠2是∠1的4倍, ∴5∠1=180°, ∴∠1=36°, ∴∠2=144°.
故答案是:144°.
15.∠BFD,两直线平行,内错角相等; BF(或FG),同位角相等,两直线平行;∠CHD(或∠CHG);∠CHD(或∠CHG),对顶角相等;
【解析】
【分析】
根据题目过程,结合平行的性质与判定即可完成.
【详解】
证明:∵AB∥CD(已知)
∴∠B= ∠BFD ( 两直线平行,内错角相等 ).
∵∠B=∠C(已知)
∴∠BFD=∠C(等量代换)
∴EC∥ BF(或FG) ( 同位角相等,两直线平行 )
∴∠2= ∠CHD(或∠CHG) (两直线平行,同位角相等)
∵∠1= ∠CHD(或∠CHG) ( 对顶角相等 )
∴∠1=∠2(等量代换).
【点睛】
本题考查平行线的性质和判定,难度较低,熟练掌握平行线的相关性质定理是解题关键.
16.详见解析
【解析】
【分析】
由AB∥CD,根据平行线的性质得∠EMB=∠MND,再根据角平分线的定义得到∠EMP=∠EMB,∠MNQ=∠MND,则∠EMP=∠MNQ,然后根据平行线的判定即可得到MP∥NQ.
【详解】
证明:∵AB∥CD,
∴∠EMB=∠MND,
∵N,MP平分∠EMB,NQ平分∠MND,
∴∠EMP=∠EMB,∠MNQ=∠MND,
∴∠EMP=∠MNQ,
∴MP∥NQ.
【点睛】
本题考查了平行线的判定与性质:两直线平行,同位角相等;同位角相等,两直线平行.
17.见解析
【解析】
【分析】
(1)首先过点P作PE∥AB,由AB∥CD,可得PE∥AB∥CD,根据两直线平行,内错角相等,即可得∠1=∠B,∠2=∠D,则可求得∠BPD=∠B+∠D.
(2)由AB∥CD,根据两直线平行,内错角相等与三角形外角的性质,即可求得∠BPD与∠B、∠D的关系.
【详解】
解:(1)∠BPD=∠B+∠D.
理由:如图2,过点P作PE∥AB,
∵AB∥CD,
∴PE∥AB∥CD,
∴∠1=∠B,∠2=∠D,
∴∠BPD=∠1+∠2=∠B+∠D;
(2)如图(3):∠BPD=∠D﹣∠B.
理由:∵AB∥CD,
∴∠1=∠D,
∵∠1=∠B+∠P,
∴∠D=∠B+∠P,
即∠BPD=∠D﹣∠B;
如图(4):∠BPD=∠B﹣∠D.
理由:∵AB∥CD,
∴∠1=∠B,
∵∠1=∠D+∠P,
∴∠B=∠D+∠P,
即∠BPD=∠B﹣∠D.
18.40°
【解析】
【分析】
根据旋转的性质得AC′=AC,∠B′AB=∠C′AC,再根据等腰三角形的性质得∠AC′C=∠ACC′,然后根据平行线的性质由CC′∥AB得∠ACC′=∠CAB=70°,则∠AC′C=∠ACC′=70°,再根据三角形内角和计算出∠CAC′=40°,所以∠B′AB=40°.
【详解】
解:∵△ABC绕点A逆时针旋转到△AB′C′的位置,
∴AC′=AC,∠B′AB=∠C′AC,
∴∠AC′C=∠ACC′,
∵CC′∥AB,
∴∠ACC′=∠CAB=70°,
∴∠AC′C=∠ACC′=70°,
∴∠CAC′=180°-2×70°=40°,
∴∠B′AB=40°.
【点睛】
本题考查了旋转的性质:旋转前后两图形全等;对应点到旋转中心的距离相等;对应点与旋转中心的连线段的夹角等于旋转角.也考查了平行线的性质.
同课章节目录
- 第一章 整式的乘除
- 1 同底数幂的乘法
- 2 幂的乘方与积的乘方
- 3 同底数幂的除法
- 4 整式的乘法
- 5 平方差公式
- 6 完全平方公式
- 7 整式的除法
- 第二章 相交线与平行线
- 1 两条直线的位置关系
- 2 探索直线平行的条件
- 3 平行线的性质
- 4 用尺规作角
- 第三章 变量之间的关系
- 1 用表格表示的变量间关系
- 2 用关系式表示的变量间关系
- 3 用图象表示的变量间关系
- 第四章 三角形
- 1 认识三角形
- 2 图形的全等
- 3 探索三角形全等的条件
- 4 用尺规作三角形
- 5 利用三角形全等测距离
- 第五章 生活中的轴对称
- 1 轴对称现象
- 2 探索轴对称的性质
- 3 简单的轴对称图形
- 4 利用轴对称进行设计
- 第六章 概率初步
- 1 感受可能性
- 2 频率的稳定性
- 3 等可能事件的概率
