北师大版七年级数学下册同步精练专题 2.2探索直线平行的条件同步训练(含解析)
文档属性
| 名称 | 北师大版七年级数学下册同步精练专题 2.2探索直线平行的条件同步训练(含解析) |  | |
| 格式 | zip | ||
| 文件大小 | 289.9KB | ||
| 资源类型 | 教案 | ||
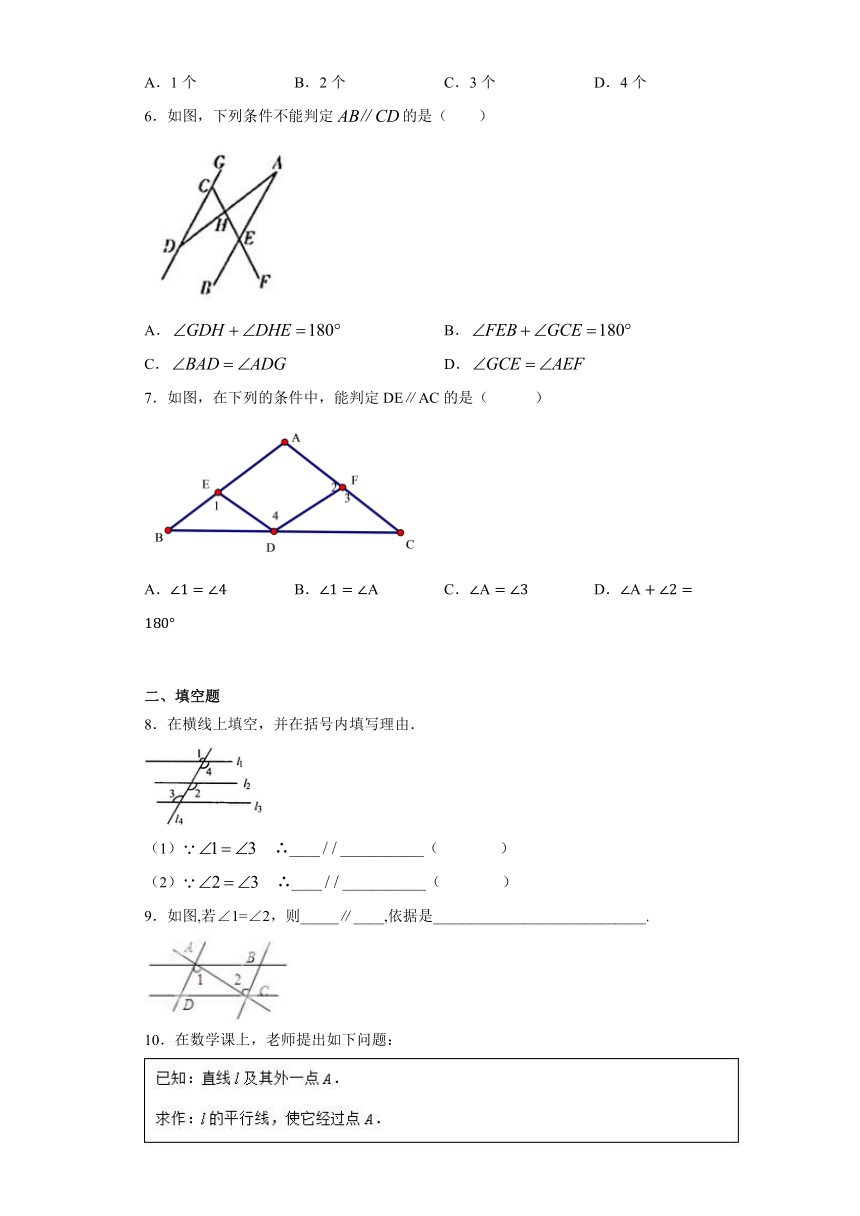
| 版本资源 | 北师大版 | ||
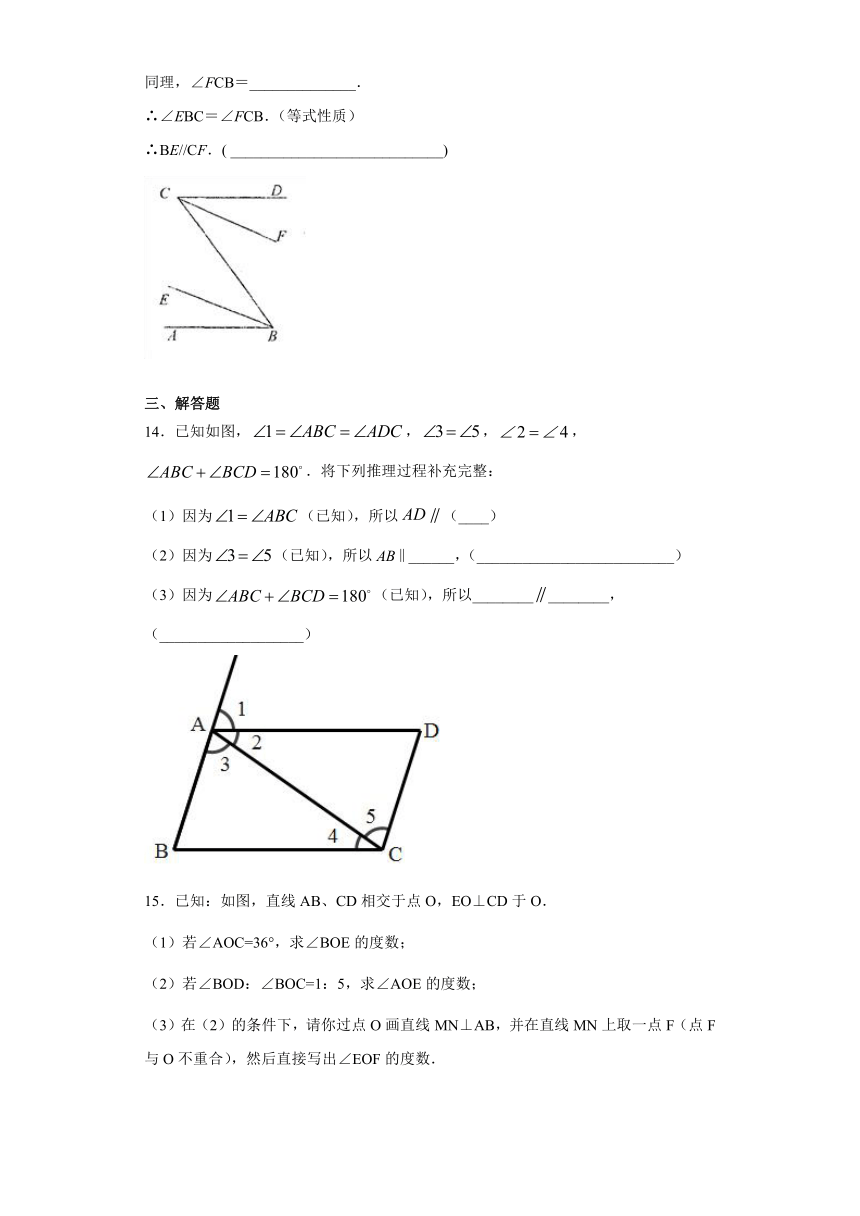
| 科目 | 数学 | ||
| 更新时间 | 2020-02-13 11:32:38 | ||
图片预览


文档简介
2.2探索直线平行的条件同步训练
学校:___________姓名:___________班级:___________考号:___________
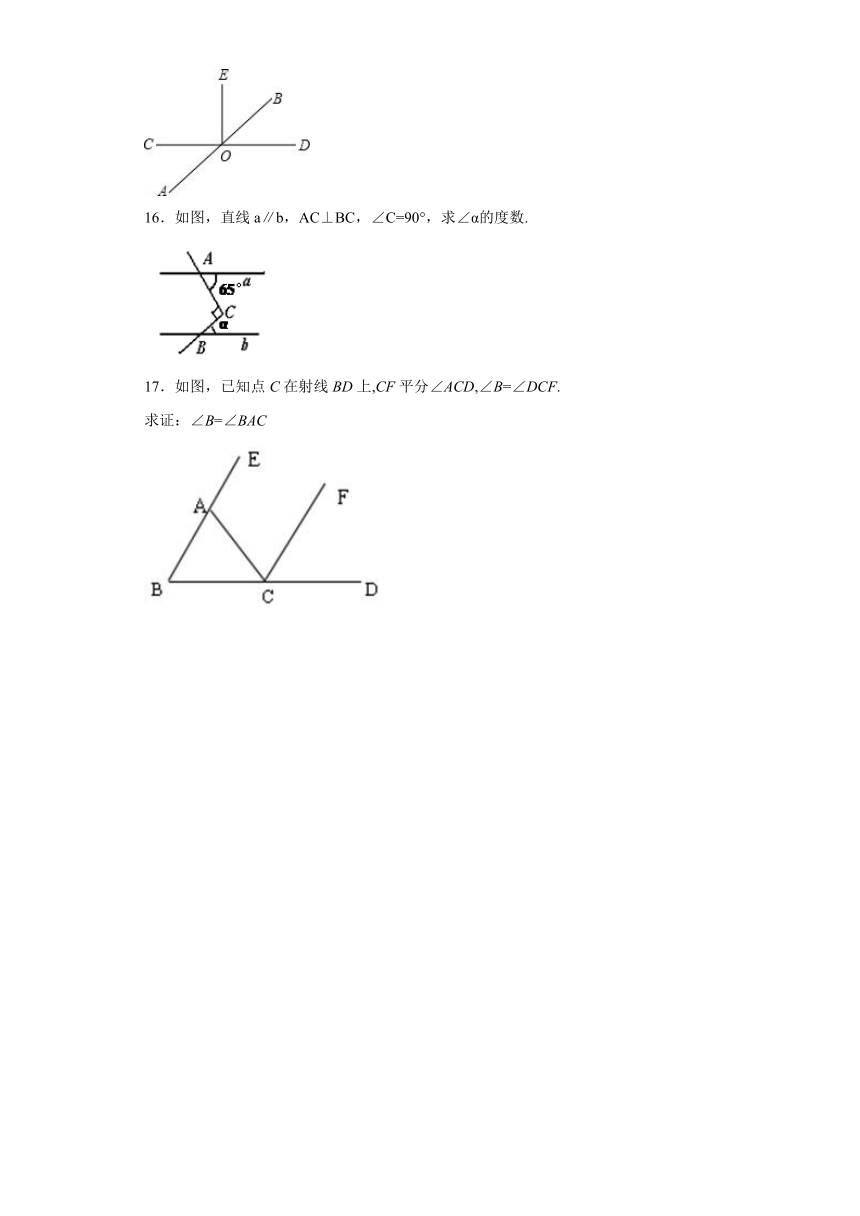
一、单选题
1.如图,在正方形中,为的中点,连结并延长,交边的延长线于点,对角线交于点,已知,则线段的长是( )
A. B. C. D.
2.直线、、在同一平面内,在下述四种说法中,正确的个数为( )
如果,,那么;
如果,,,那么;
如果,,那么;
如果与相交,与相交,那么与相交.
A.1个 B.2个 C.3个 D.4个
3.若∠α与∠β的两边分别平行,且∠α=(2x+10)°,∠β=(3x﹣20)°,则∠α的度数为( )
A.70° B.86° C.70°或86° D.30°或38°
4.下面说法正确的是( )
A.射线AB与射线BA是同一条射线 B.平角是一条直线
C.小于平角的角是钝角 D.两点之间的所有连线中,线段最短
5.如图,已知,下列结论正确的有( )
①若,则;②若,则;③若,则;④若,则.
A.1个 B.2个 C.3个 D.4个
6.如图,下列条件不能判定的是( )
A. B.
C. D.
7.如图,在下列的条件中,能判定DE∥AC的是( )
A.∠1=∠4 B.∠1=∠A C.∠A=∠3 D.∠A+∠2=180°
二、填空题
8.在横线上填空,并在括号内填写理由.
(1) ∴_______________( )
(2) ∴_______________( )
9.如图,若∠1=∠2,则_____∥____,依据是____________________________.
10.在数学课上,老师提出如下问题:
小菲用两块形状、大小相同的三角尺完成了该题的作图,作法如下:
如图,
(1)用第一块三角尺的一条边贴住直线l,第二块三角尺的一条边紧靠第一块三角尺;
(2)将第二块三角尺沿第一块三角尺移动,使其另一边经过点A,沿这边作出直线AB.
所以,直线AB即为所求.
老师说:“小菲的作法正确.”
请回答:小菲的作图依据是________________.
11.如图,点E在BC的延长线上,下列条件中能判定AB∥CD的是__________(请填写正确的序号)①∠3=∠4 ②∠1=∠2 ③∠B=∠DCE ④∠D+∠DAB=180°
12.如图,下列条件①,②,③,④,⑤,能判断的是____.
13.在下列解题过程的空白处填上适当的内容(推理的理由或数学表达式)
如图,已知AB∥CD,BE、CF分别平分∠ABC和∠DCB,求证:BE∥CF.
证明:∵AB∥CD,(已知)
∴∠_______=∠_______.(_________________________)
∵__________________________________________,(已知)
∴∠EBC=_______,(角平分线定义)
同理,∠FCB=______________.
∴∠EBC=∠FCB.(等式性质)
∴BE//CF.( ____________________________)
三、解答题
14.已知如图,,,, .将下列推理过程补充完整:
(1)因为(已知),所以(____)
(2)因为(已知),所以______,(__________________________)
(3)因为(已知),所以________________,(___________________)
15.已知:如图,直线AB、CD相交于点O,EO⊥CD于O.
(1)若∠AOC=36°,求∠BOE的度数;
(2)若∠BOD:∠BOC=1:5,求∠AOE的度数;
(3)在(2)的条件下,请你过点O画直线MN⊥AB,并在直线MN上取一点F(点F与O不重合),然后直接写出∠EOF的度数.
16.如图,直线a∥b,AC⊥BC,∠C=90°,求∠α的度数.
17.如图,已知点C在射线BD上,CF平分∠ACD,∠B=∠DCF.
求证:∠B=∠BAC
参考答案
1.D
【解析】
【分析】
根据正方形的性质可得出AB∥CD,进而可得出△ABF∽△GDF,根据相似三角形的性质可得出,结合FG=2可求出AF、AG的长度,由CG∥AB、AB=2CG可得出CG为△EAB的中位线,再利用三角形中位线的性质可求出AE的长度,此题得解.
【详解】
解:∵四边形ABCD为正方形,
∴AB=CD,AB∥CD,
∴∠ABF=∠GDF,∠BAF=∠DGF,
∴△ABF∽△GDF,
∴,
∴AF=2GF=4,
∴AG=6,
∵CG∥AB,AB=2CG,
∴CG为△EAB的中位线,
∴AE=2AG=12,
故选D.
【点睛】
本题考查了相似三角形的判定与性质、正方形的性质以及三角形的中位线,利用相似三角形的性质求出AF的长度是解题的关键.
2.C
【解析】
【分析】
根据同一平面内垂直于同一直线的两直线平行,平行公理对各小题分析判断即可得解.
【详解】
解:如果,,那么,正确;
如果,,,那么,正确;
如果,,那么,正确;
如果与相交,与相交,那么与相交或平行,故本小题错误.
综上所述,正确的个数是个.
故选.
【点睛】
本题考查平行线与相交线,熟练掌握基础知识是解题关键.
3.D
【解析】试题解析:∵∠α与∠β的两边分别平行,且∠α=(2x+10)°,∠β=(3x-20)°,
∴(2x+10)+(3x-20)=180,2x+10=3x-20,
x=38,x=30,
当x=38时,∠α=86°,
当x=30时,∠α=70°,
故选C.
4.D
【解析】
【分析】
根据角与直线的定义即可判断.
【详解】
A. 射线AB与射线BA,起点不同,不是同一条射线,故错误;
B. 平角是一个角,由一个顶点和两条射线组成,故错误;
C. 小于平角的角可以是钝角、直角、锐角,故错误;
D. 两点之间的所有连线中,线段最短,正确,
故选D.
【点睛】
此题主要考查直线与角的定义,解题的关键是熟知基本图形的定义及特点.
5.B
【解析】
【分析】
根据∠1=30°求出∠3=∠2=150°,推出∠2=∠4,∠3=∠4,根据平行线的判定推出即可.
【详解】
∵∠1=30°,∴∠2=150°,
∴①错误;
∵∠4=150°,
∴∠2=∠4,
∴AB∥CD(同位角相等,两直线平行),
∴④正确;
∵∠1=30°,
∴∠3=150°,
∵∠5=30°,
∴∠4=150°,
∴∠3=∠4,
∴AB∥CD(内错角相等,两直线平行),
∴②正确;
根据∠1=30°,∠3=150°不能推出AB∥CD,
∴③错误;
即正确的个数是2个,
故选B.
【点睛】
此题考查平行线的判定,解题关键在于掌握判定定理.
6.A
【解析】
【分析】
根据同位角相等,两直线平行;内错角相等,两直线平行;同旁内角互补,两直线平行;即可判断出正确答案.
【详解】
根据 ,不能得到 ,故A选项不能判定;
根据 ,,可得,进而得到,故B选项能判定;
根据,可得,故C选项能判定;
根据,可得,故D选项能判定;
故选A.
【点睛】
本题主要考查了平行线的判定,解题时注意,同位角相等,两直线平行;内错角相等,两直线平行;同旁内角互补,两直线平行.
7.B
【解析】
【分析】
可以从直线DE,AC的截线所组成的“三线八角"图形入手进行判断.
【详解】
解:由∠1=∠4,可判定AB∥DF,不能判定DE//AC,故A选项错误;
由∠1=∠A,可得DE//AC,故B选项正确;
由∠A=∠3,可判定AB∥DF,不能判定DE//AC,故C选项错误;
由∠A+∠2=180°可判定AB∥DF,不能判定DE//AC, 故D选项错误;
故选:B.
【点睛】
本题考查平行线的判定,关键是对平行线的判定方法灵活应用.
8.(1);;同位角相等,两直线平行(2);;内错角相等,两直线平行.
【解析】
【分析】
根据平行线的判定方法:同位角相等,两直线平行;内错角相等,两直线平行,进行分析即可.
【详解】
(1),
∴∥(同位角相等,两直线平行)
(2) ,
∴. (内错角相等,两直线平行)
【点睛】
本题考查了平行线的判定,熟练掌握平行线的判定是解题的关键.
9.AD BC 内错角相等,两直线平行
【解析】
【详解】
∵∠1=∠2,∠1和∠2是直线AD、BC被直线AC所截而形成的内错角,
∴AD//BC(内错角相等,两直线平行).
故答案是:AD; BC;内错角相等,两直线平行.
10.内错角相等,两条直线平行
【解析】
【分析】
根据平行线的判定方法分析即可.
【详解】
由作法可知,∠1与∠2是一对内错角,且∠1=∠2,
∴小菲的作图依据是:内错角相等,两条直线平行.
故答案为:内错角相等,两条直线平行
【点睛】
本题考查了平行线的判定方法:①两同位角相等,两直线平行;?②内错角相等,两直线平行;③同旁内角互补,两直线平行;④平行于同一直线的两条直线互相平行;同一平面内,垂直于同一直线的两条直线互相平行.
11.②③④
【解析】
【分析】
根据平行线的判定定理对四个选项进行逐一分析即可
【详解】
①.由∠3=∠4可以判定AD∥BC,不能判断AB∥CD,故本选项错误;
②. 由∠1=∠2可以判定AB∥CD,依据是内错角相等,两直线平行,故本选项正确;
③.由∠B=∠DCE能判断AB∥CD,依据同位角相等,两直线平行,故本选项正确;
④. 由∠D+∠DAB=180°可以判定AB∥CD ,故本选项正确;
故答案为②③④
【点睛】
此题考查平行线的判定,难度不大,解题关键在于掌握平行线的性质
12.①④
【解析】
【分析】
根据平行线的判定即可解题.
【详解】
解:①,根据内错角相等可以判断.
②,得到的是AC∥BD,
③,得到的是AC∥BD,
④,可以判断.
⑤,判断不出平行,
所以答案是①④
【点睛】
本题考查了平行线的判定,属于简单题,熟悉平行线的判定定理,找到对应的内错角和同旁内角是解题关键.
13.答案见解析
【解析】
证明:∵AB∥CD,(已知)
∴∠_ABC__=∠__DCB__.(__两直线平行,内错角相等__)
∵____ BE、CF分别平分∠ABC和∠DCB ___,(已知)
∴∠EBC=_∠ABC_,(角平分线定义)
同理,∠FCB=__∠DCB_,_.
∴∠EBC=∠FCB.(等式性质)
∴BE//CF.( _内错角相等,两直线平行__)
14.(1)BC,同位角相等两直线平行;(2)CD,内错角相等两直线平行;(3),同旁内角互补两直线平行.
【解析】
【分析】
(1)利用同位角相等,两直线平行进行推理;(2)利用内错角相等,两直线平行进行推理;(3)根据同旁内角互补,两直线平行进行推理.
【详解】
解:(1)∵(已知),
∴,(同位角相等,两直线平行)
(2)∵(已知),
∴,(内错角相等,两直线平行)
(3)∵(已知),
∴.(同旁内角互补,两直线平行)
【点睛】
本题考查平行线的判定,熟记判定方法进行推理是本题的解题关键.
15.(1)54°;(2)120°;(3)∠EOF的度数为30°或150°.
【解析】
【分析】
(1)依据垂线的定义以及对顶角相等,即可得∠BOE的度数;
(2)依据平角的定义以及垂线的定义,即可得到∠AOE的度数;
(3)分两种情况:若F在射线OM上,则∠EOF=∠BOD=30°;若F'在射线ON上,则∠EOF'=∠DOE+∠BON-∠BOD=150°.
【详解】
解:(1)∵EO⊥CD,
∴∠DOE=90°,
又∵∠BOD=∠AOC=36°,
∴∠BOE=90°-36°=54°;
(2)∵∠BOD:∠BOC=1:5,
∴∠BOD=∠COD=30°,
∴∠AOC=30°,
又∵EO⊥CD,
∴∠COE=90°,
∴∠AOE=90°+30°=120°;
(3)分两种情况:
若F在射线OM上,则∠EOF=∠BOD=30°;
若F'在射线ON上,则∠EOF'=∠DOE+∠BON-∠BOD=150°;
综上所述,∠EOF的度数为30°或150°.
故答案为(1)54°;(2)120°;(3)∠EOF的度数为30°或150°.
【点睛】
本题考查了角的计算,对顶角,垂线等知识点的应用,关键是分类讨论思想的运用.
16.25°
【解析】
【分析】
过点C作CE∥a,运用平行线的性质,证明∠ACE=65°,∠α=∠BCE,再运用垂直求∠α的度数.
【详解】
解:过点C作CE∥a,
∵a∥b,
∴CE∥a∥b,
∴∠ACE=65°,∠α=∠BCE.
∵∠C=90°,
∴∠α=∠BCE=90°﹣∠ACE=25°.
【点睛】
考点:平行线的性质.
17.证明见解析
【解析】试题分析:由∠B=∠DCF得BE∥CF,从而∠ACF=∠BAC,再由CF平分∠ACD知,∠ACF=∠DCF,故可得结论.
试题解析:证明:∵∠B=∠DCF,∴BE∥CF
∴∠ACF=∠BAC
∵CF平分∠ACD,∴∠ACF=∠DCF
∴∠BAC=∠DCF
∴∠B=∠BAC
学校:___________姓名:___________班级:___________考号:___________
一、单选题
1.如图,在正方形中,为的中点,连结并延长,交边的延长线于点,对角线交于点,已知,则线段的长是( )
A. B. C. D.
2.直线、、在同一平面内,在下述四种说法中,正确的个数为( )
如果,,那么;
如果,,,那么;
如果,,那么;
如果与相交,与相交,那么与相交.
A.1个 B.2个 C.3个 D.4个
3.若∠α与∠β的两边分别平行,且∠α=(2x+10)°,∠β=(3x﹣20)°,则∠α的度数为( )
A.70° B.86° C.70°或86° D.30°或38°
4.下面说法正确的是( )
A.射线AB与射线BA是同一条射线 B.平角是一条直线
C.小于平角的角是钝角 D.两点之间的所有连线中,线段最短
5.如图,已知,下列结论正确的有( )
①若,则;②若,则;③若,则;④若,则.
A.1个 B.2个 C.3个 D.4个
6.如图,下列条件不能判定的是( )
A. B.
C. D.
7.如图,在下列的条件中,能判定DE∥AC的是( )
A.∠1=∠4 B.∠1=∠A C.∠A=∠3 D.∠A+∠2=180°
二、填空题
8.在横线上填空,并在括号内填写理由.
(1) ∴_______________( )
(2) ∴_______________( )
9.如图,若∠1=∠2,则_____∥____,依据是____________________________.
10.在数学课上,老师提出如下问题:
小菲用两块形状、大小相同的三角尺完成了该题的作图,作法如下:
如图,
(1)用第一块三角尺的一条边贴住直线l,第二块三角尺的一条边紧靠第一块三角尺;
(2)将第二块三角尺沿第一块三角尺移动,使其另一边经过点A,沿这边作出直线AB.
所以,直线AB即为所求.
老师说:“小菲的作法正确.”
请回答:小菲的作图依据是________________.
11.如图,点E在BC的延长线上,下列条件中能判定AB∥CD的是__________(请填写正确的序号)①∠3=∠4 ②∠1=∠2 ③∠B=∠DCE ④∠D+∠DAB=180°
12.如图,下列条件①,②,③,④,⑤,能判断的是____.
13.在下列解题过程的空白处填上适当的内容(推理的理由或数学表达式)
如图,已知AB∥CD,BE、CF分别平分∠ABC和∠DCB,求证:BE∥CF.
证明:∵AB∥CD,(已知)
∴∠_______=∠_______.(_________________________)
∵__________________________________________,(已知)
∴∠EBC=_______,(角平分线定义)
同理,∠FCB=______________.
∴∠EBC=∠FCB.(等式性质)
∴BE//CF.( ____________________________)
三、解答题
14.已知如图,,,, .将下列推理过程补充完整:
(1)因为(已知),所以(____)
(2)因为(已知),所以______,(__________________________)
(3)因为(已知),所以________________,(___________________)
15.已知:如图,直线AB、CD相交于点O,EO⊥CD于O.
(1)若∠AOC=36°,求∠BOE的度数;
(2)若∠BOD:∠BOC=1:5,求∠AOE的度数;
(3)在(2)的条件下,请你过点O画直线MN⊥AB,并在直线MN上取一点F(点F与O不重合),然后直接写出∠EOF的度数.
16.如图,直线a∥b,AC⊥BC,∠C=90°,求∠α的度数.
17.如图,已知点C在射线BD上,CF平分∠ACD,∠B=∠DCF.
求证:∠B=∠BAC
参考答案
1.D
【解析】
【分析】
根据正方形的性质可得出AB∥CD,进而可得出△ABF∽△GDF,根据相似三角形的性质可得出,结合FG=2可求出AF、AG的长度,由CG∥AB、AB=2CG可得出CG为△EAB的中位线,再利用三角形中位线的性质可求出AE的长度,此题得解.
【详解】
解:∵四边形ABCD为正方形,
∴AB=CD,AB∥CD,
∴∠ABF=∠GDF,∠BAF=∠DGF,
∴△ABF∽△GDF,
∴,
∴AF=2GF=4,
∴AG=6,
∵CG∥AB,AB=2CG,
∴CG为△EAB的中位线,
∴AE=2AG=12,
故选D.
【点睛】
本题考查了相似三角形的判定与性质、正方形的性质以及三角形的中位线,利用相似三角形的性质求出AF的长度是解题的关键.
2.C
【解析】
【分析】
根据同一平面内垂直于同一直线的两直线平行,平行公理对各小题分析判断即可得解.
【详解】
解:如果,,那么,正确;
如果,,,那么,正确;
如果,,那么,正确;
如果与相交,与相交,那么与相交或平行,故本小题错误.
综上所述,正确的个数是个.
故选.
【点睛】
本题考查平行线与相交线,熟练掌握基础知识是解题关键.
3.D
【解析】试题解析:∵∠α与∠β的两边分别平行,且∠α=(2x+10)°,∠β=(3x-20)°,
∴(2x+10)+(3x-20)=180,2x+10=3x-20,
x=38,x=30,
当x=38时,∠α=86°,
当x=30时,∠α=70°,
故选C.
4.D
【解析】
【分析】
根据角与直线的定义即可判断.
【详解】
A. 射线AB与射线BA,起点不同,不是同一条射线,故错误;
B. 平角是一个角,由一个顶点和两条射线组成,故错误;
C. 小于平角的角可以是钝角、直角、锐角,故错误;
D. 两点之间的所有连线中,线段最短,正确,
故选D.
【点睛】
此题主要考查直线与角的定义,解题的关键是熟知基本图形的定义及特点.
5.B
【解析】
【分析】
根据∠1=30°求出∠3=∠2=150°,推出∠2=∠4,∠3=∠4,根据平行线的判定推出即可.
【详解】
∵∠1=30°,∴∠2=150°,
∴①错误;
∵∠4=150°,
∴∠2=∠4,
∴AB∥CD(同位角相等,两直线平行),
∴④正确;
∵∠1=30°,
∴∠3=150°,
∵∠5=30°,
∴∠4=150°,
∴∠3=∠4,
∴AB∥CD(内错角相等,两直线平行),
∴②正确;
根据∠1=30°,∠3=150°不能推出AB∥CD,
∴③错误;
即正确的个数是2个,
故选B.
【点睛】
此题考查平行线的判定,解题关键在于掌握判定定理.
6.A
【解析】
【分析】
根据同位角相等,两直线平行;内错角相等,两直线平行;同旁内角互补,两直线平行;即可判断出正确答案.
【详解】
根据 ,不能得到 ,故A选项不能判定;
根据 ,,可得,进而得到,故B选项能判定;
根据,可得,故C选项能判定;
根据,可得,故D选项能判定;
故选A.
【点睛】
本题主要考查了平行线的判定,解题时注意,同位角相等,两直线平行;内错角相等,两直线平行;同旁内角互补,两直线平行.
7.B
【解析】
【分析】
可以从直线DE,AC的截线所组成的“三线八角"图形入手进行判断.
【详解】
解:由∠1=∠4,可判定AB∥DF,不能判定DE//AC,故A选项错误;
由∠1=∠A,可得DE//AC,故B选项正确;
由∠A=∠3,可判定AB∥DF,不能判定DE//AC,故C选项错误;
由∠A+∠2=180°可判定AB∥DF,不能判定DE//AC, 故D选项错误;
故选:B.
【点睛】
本题考查平行线的判定,关键是对平行线的判定方法灵活应用.
8.(1);;同位角相等,两直线平行(2);;内错角相等,两直线平行.
【解析】
【分析】
根据平行线的判定方法:同位角相等,两直线平行;内错角相等,两直线平行,进行分析即可.
【详解】
(1),
∴∥(同位角相等,两直线平行)
(2) ,
∴. (内错角相等,两直线平行)
【点睛】
本题考查了平行线的判定,熟练掌握平行线的判定是解题的关键.
9.AD BC 内错角相等,两直线平行
【解析】
【详解】
∵∠1=∠2,∠1和∠2是直线AD、BC被直线AC所截而形成的内错角,
∴AD//BC(内错角相等,两直线平行).
故答案是:AD; BC;内错角相等,两直线平行.
10.内错角相等,两条直线平行
【解析】
【分析】
根据平行线的判定方法分析即可.
【详解】
由作法可知,∠1与∠2是一对内错角,且∠1=∠2,
∴小菲的作图依据是:内错角相等,两条直线平行.
故答案为:内错角相等,两条直线平行
【点睛】
本题考查了平行线的判定方法:①两同位角相等,两直线平行;?②内错角相等,两直线平行;③同旁内角互补,两直线平行;④平行于同一直线的两条直线互相平行;同一平面内,垂直于同一直线的两条直线互相平行.
11.②③④
【解析】
【分析】
根据平行线的判定定理对四个选项进行逐一分析即可
【详解】
①.由∠3=∠4可以判定AD∥BC,不能判断AB∥CD,故本选项错误;
②. 由∠1=∠2可以判定AB∥CD,依据是内错角相等,两直线平行,故本选项正确;
③.由∠B=∠DCE能判断AB∥CD,依据同位角相等,两直线平行,故本选项正确;
④. 由∠D+∠DAB=180°可以判定AB∥CD ,故本选项正确;
故答案为②③④
【点睛】
此题考查平行线的判定,难度不大,解题关键在于掌握平行线的性质
12.①④
【解析】
【分析】
根据平行线的判定即可解题.
【详解】
解:①,根据内错角相等可以判断.
②,得到的是AC∥BD,
③,得到的是AC∥BD,
④,可以判断.
⑤,判断不出平行,
所以答案是①④
【点睛】
本题考查了平行线的判定,属于简单题,熟悉平行线的判定定理,找到对应的内错角和同旁内角是解题关键.
13.答案见解析
【解析】
证明:∵AB∥CD,(已知)
∴∠_ABC__=∠__DCB__.(__两直线平行,内错角相等__)
∵____ BE、CF分别平分∠ABC和∠DCB ___,(已知)
∴∠EBC=_∠ABC_,(角平分线定义)
同理,∠FCB=__∠DCB_,_.
∴∠EBC=∠FCB.(等式性质)
∴BE//CF.( _内错角相等,两直线平行__)
14.(1)BC,同位角相等两直线平行;(2)CD,内错角相等两直线平行;(3),同旁内角互补两直线平行.
【解析】
【分析】
(1)利用同位角相等,两直线平行进行推理;(2)利用内错角相等,两直线平行进行推理;(3)根据同旁内角互补,两直线平行进行推理.
【详解】
解:(1)∵(已知),
∴,(同位角相等,两直线平行)
(2)∵(已知),
∴,(内错角相等,两直线平行)
(3)∵(已知),
∴.(同旁内角互补,两直线平行)
【点睛】
本题考查平行线的判定,熟记判定方法进行推理是本题的解题关键.
15.(1)54°;(2)120°;(3)∠EOF的度数为30°或150°.
【解析】
【分析】
(1)依据垂线的定义以及对顶角相等,即可得∠BOE的度数;
(2)依据平角的定义以及垂线的定义,即可得到∠AOE的度数;
(3)分两种情况:若F在射线OM上,则∠EOF=∠BOD=30°;若F'在射线ON上,则∠EOF'=∠DOE+∠BON-∠BOD=150°.
【详解】
解:(1)∵EO⊥CD,
∴∠DOE=90°,
又∵∠BOD=∠AOC=36°,
∴∠BOE=90°-36°=54°;
(2)∵∠BOD:∠BOC=1:5,
∴∠BOD=∠COD=30°,
∴∠AOC=30°,
又∵EO⊥CD,
∴∠COE=90°,
∴∠AOE=90°+30°=120°;
(3)分两种情况:
若F在射线OM上,则∠EOF=∠BOD=30°;
若F'在射线ON上,则∠EOF'=∠DOE+∠BON-∠BOD=150°;
综上所述,∠EOF的度数为30°或150°.
故答案为(1)54°;(2)120°;(3)∠EOF的度数为30°或150°.
【点睛】
本题考查了角的计算,对顶角,垂线等知识点的应用,关键是分类讨论思想的运用.
16.25°
【解析】
【分析】
过点C作CE∥a,运用平行线的性质,证明∠ACE=65°,∠α=∠BCE,再运用垂直求∠α的度数.
【详解】
解:过点C作CE∥a,
∵a∥b,
∴CE∥a∥b,
∴∠ACE=65°,∠α=∠BCE.
∵∠C=90°,
∴∠α=∠BCE=90°﹣∠ACE=25°.
【点睛】
考点:平行线的性质.
17.证明见解析
【解析】试题分析:由∠B=∠DCF得BE∥CF,从而∠ACF=∠BAC,再由CF平分∠ACD知,∠ACF=∠DCF,故可得结论.
试题解析:证明:∵∠B=∠DCF,∴BE∥CF
∴∠ACF=∠BAC
∵CF平分∠ACD,∴∠ACF=∠DCF
∴∠BAC=∠DCF
∴∠B=∠BAC
同课章节目录
- 第一章 整式的乘除
- 1 同底数幂的乘法
- 2 幂的乘方与积的乘方
- 3 同底数幂的除法
- 4 整式的乘法
- 5 平方差公式
- 6 完全平方公式
- 7 整式的除法
- 第二章 相交线与平行线
- 1 两条直线的位置关系
- 2 探索直线平行的条件
- 3 平行线的性质
- 4 用尺规作角
- 第三章 变量之间的关系
- 1 用表格表示的变量间关系
- 2 用关系式表示的变量间关系
- 3 用图象表示的变量间关系
- 第四章 三角形
- 1 认识三角形
- 2 图形的全等
- 3 探索三角形全等的条件
- 4 用尺规作三角形
- 5 利用三角形全等测距离
- 第五章 生活中的轴对称
- 1 轴对称现象
- 2 探索轴对称的性质
- 3 简单的轴对称图形
- 4 利用轴对称进行设计
- 第六章 概率初步
- 1 感受可能性
- 2 频率的稳定性
- 3 等可能事件的概率
