四年级下册数学课件-三角形内角和-人教版(34张ppt)
文档属性
| 名称 | 四年级下册数学课件-三角形内角和-人教版(34张ppt) |  | |
| 格式 | zip | ||
| 文件大小 | 1.2MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-02-13 19:20:30 | ||
图片预览




文档简介
(共34张PPT)
三角形的内角和
实验小学
小学数学四年下册
什么是三角形的内角?
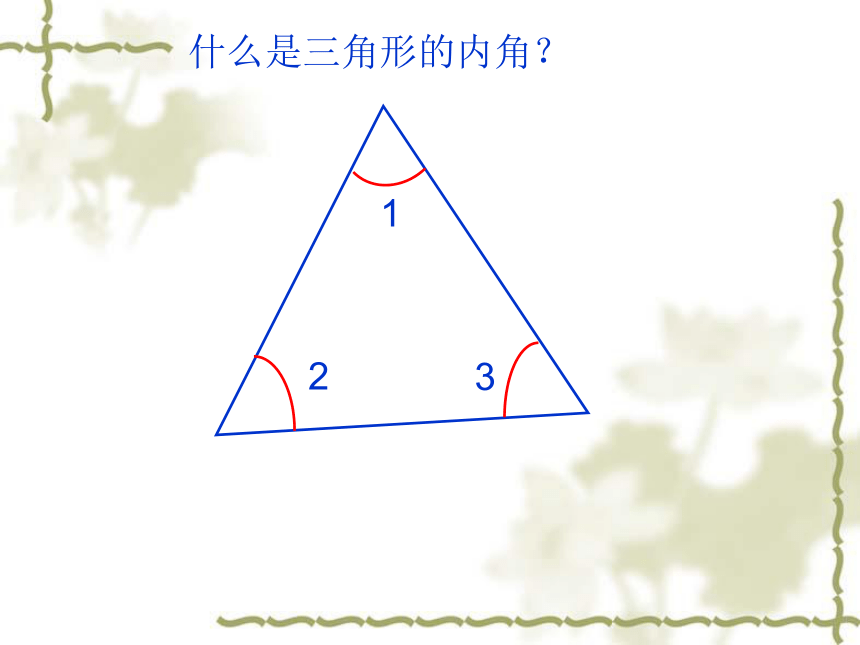
1
2
3
什么是三角形的内角?
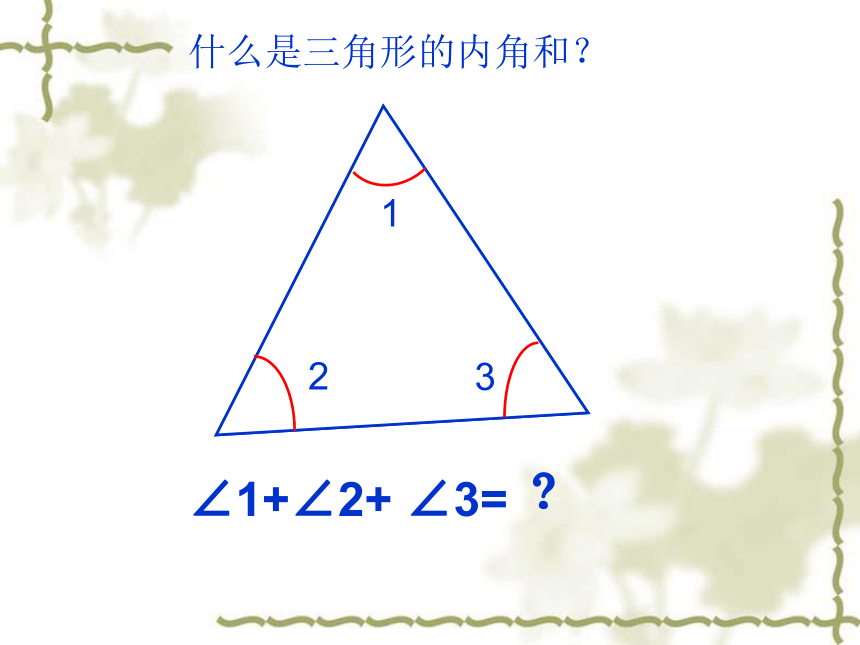
∠1+∠2+ ∠3=﹖
什么是三角形的内角和?
1
2
3
一、量一量
测量分工要求:?
1?、 每小组选出锐角三角形、直角三角形、钝角三角形 各两个。每人测量一个。
2、 把角标上序号,量出度数,求出内角和。
3、 汇报给小组长,小组长负责记录。?
4? 、小组长要监督小组其他同学量的是不是很准确、真实,不能改掉小组成员度量出来的数据。??
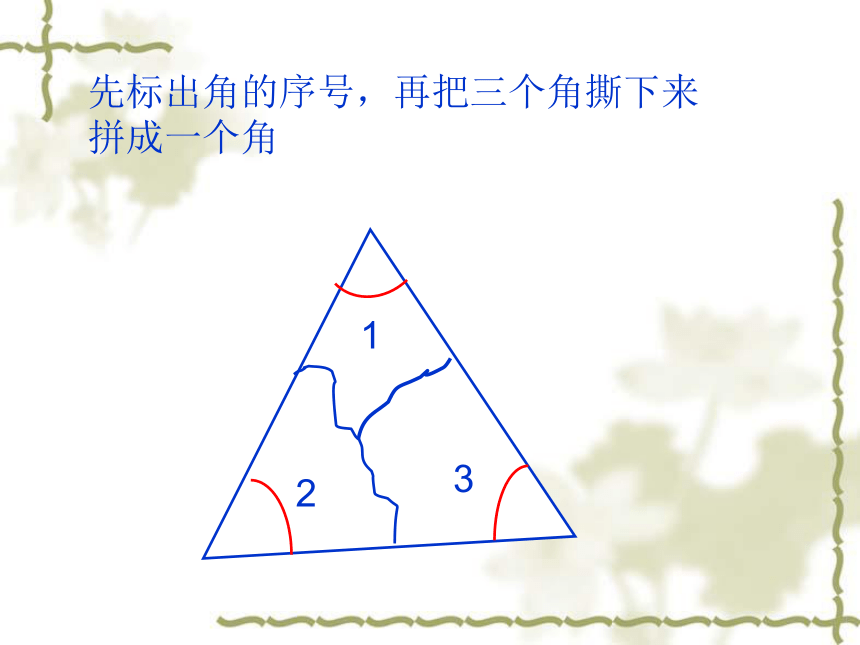
二、拼一拼
1
2
3
先标出角的序号,再把三个角撕下来
拼成一个角
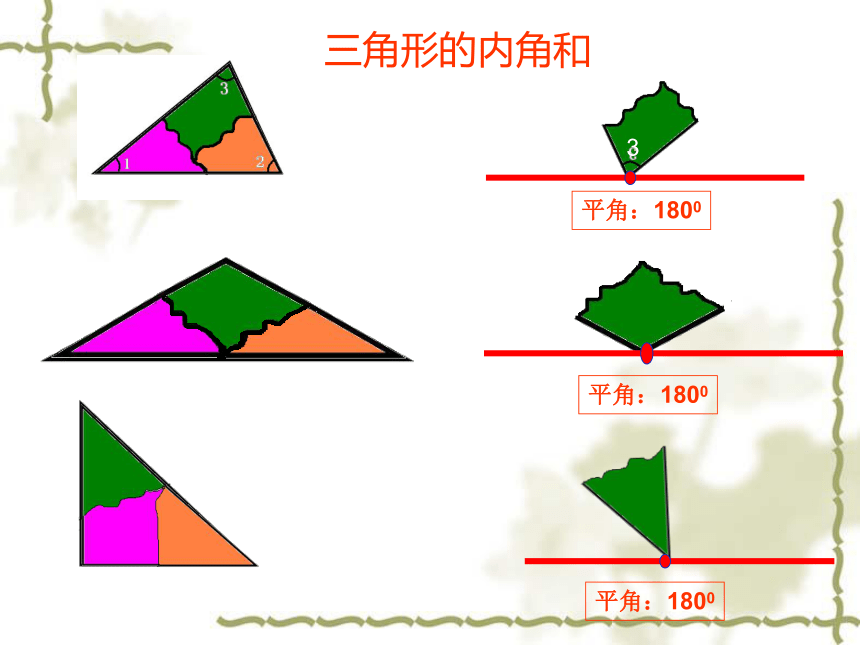
三角形的内角和
平角:1800
平角:1800
平角:1800
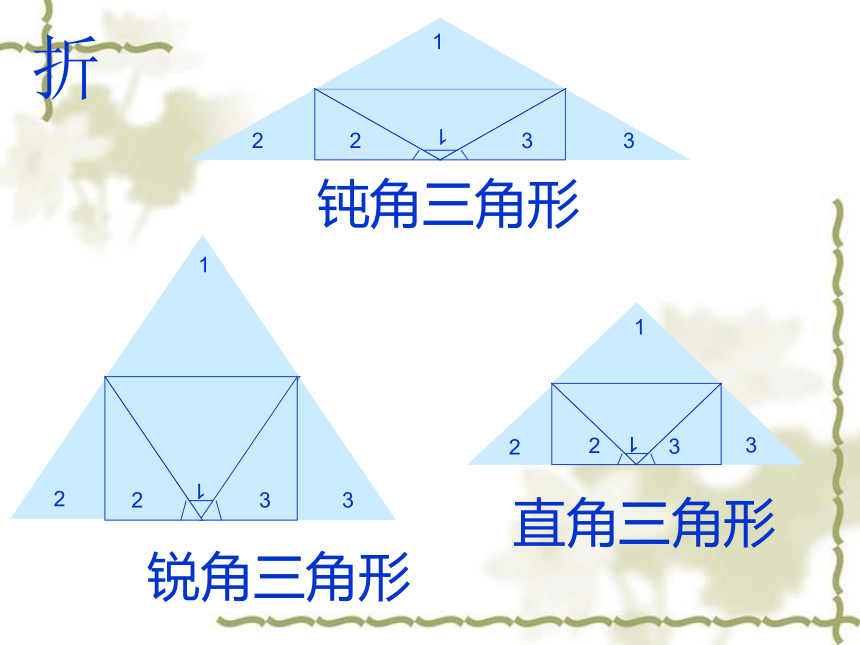
钝角三角形
锐角三角形
直角三角形
折
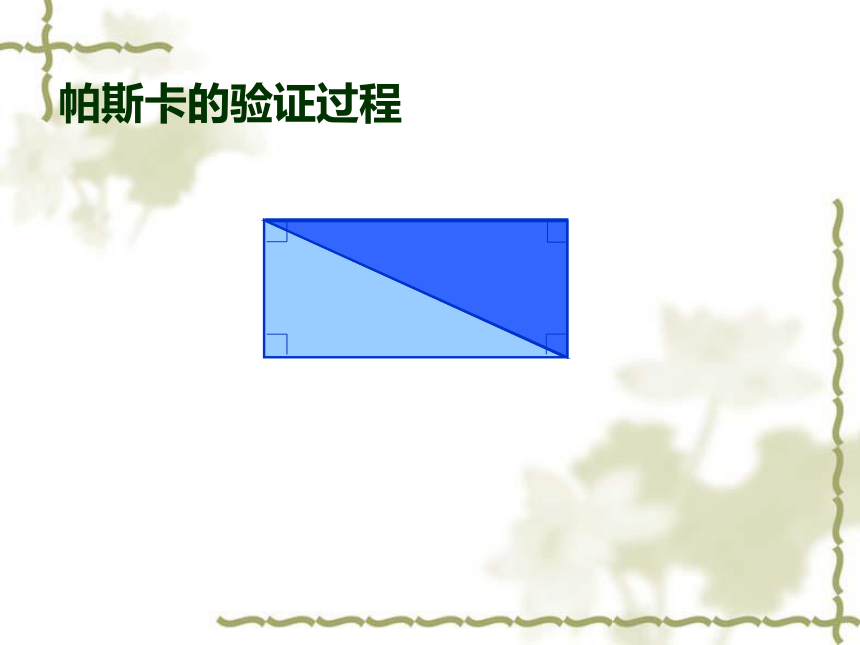
法国著名的数学家、物理学家。12岁时发现“任意三角形的内角和都是180?”。
布莱士·帕斯卡
(1623—1662)
帕斯卡的验证过程
360°÷ 2 = 180°
直角三角形内角和
180°
180°
180°×2
-180°
=180°
锐角三角形内角和
180°
180°
180°×2-180°=180°
钝角三角形内角和
三、结论
三角形的内角和是180°
?
72°
28°
180°--(72°+28°)=80°
四、练习
猜角
三角形∠1=140°∠3=25°求∠2的度数。
180°-140°-25°
=140°-25°
=15°
180 °-(140° +25°)
=180 °-165°
=15°
猜猜我们多少度?
我是等边三角形,我的一个角多少度?
?度
猜猜我们多少度?
我是等腰直角三角形,我的一个底角多少度?
?度
猜角
如下图,求∠1的度数。
判断
1、三角形越大,内角和越大。
2、一个三角形中最多有一个直角或钝角。
3、两个三角形拼成一个大三角形,这个大三角形的内角和是360 °。
(×)
(√ )
(× )
一个等腰三角形的风筝,它的一个底角是700,它的顶角是多少度?
一个等腰三角形的风筝,它的一个底角是700,它的顶角是多少度?
1800-700×2
=1800 -1400
=400
1800-700 -700
=1100 -700
=400
700
700
400
答:它的顶角是400。
家里镜框上的一块三角形玻璃碎了(如图)。聪明的明明,只带了其中的一块去玻璃店,就配到了和原来一模一样的。你知道他带的是哪一块吗?
知识的升华
你能根据三角形的内角和求出四边形、五边形、六边形的内角和吗?
两个三角形:180°×2=360 °
三个三角形: 180°×3=540 °
4个三角形:180°×4=720°
知识的升华
多边形 边数 三角形个数 多边形的内角和
四边形 4 2 2×180°
五边形 5 3 3 ×180°
六边形 6 4 4 ×180°
七边形
知识的升华
多边形 边数 三角形个数 多边形的内角和
四边形 4 2 2×180°
五边形 5 3 3 ×180°
六边形 6 4 4 ×180°
七边形 7 5
n边形
知识的升华
多边形 边数 三角形个数 多边形的内角和
四边形 4 2 2×180°
五边形 5 3 3 ×180°
六边形 6 4 4 ×180°
七边形 7 5 5 ×180°
n边形
知识的升华
多边形 边数 三角形个数 多边形的内角和
四边形 4 2 2×180°
五边形 5 3 3 ×180°
六边形 6 4 4 ×180°
七边形 7 5 5 ×180°
n边形 n n-2
知识的升华
多边形 边数 三角形个数 多边形的内角和
四边形 4 2 2×180°
五边形 5 3 3 ×180°
六边形 6 4 4 ×180°
七边形 7 5 5 ×180°
N边形 n n-2
知识的升华
多边形 边数 三角形个数 多边形的内角和
四边形 4 2 2×180°
五边形 5 3 3 ×180°
六边形 6 4 4 ×180°
七边形 7 5 5 ×180°
n边形 n n-2 (n-2)×180°
知识的升华
多边形 边数 三角形个数 多边形的内角和
四边形 4 2
(边数-2)×180°
五边形 5 3
六边形 6 4
七边形 7 5
n边形 n n-2
三角形的内角和
实验小学
小学数学四年下册
什么是三角形的内角?
1
2
3
什么是三角形的内角?
∠1+∠2+ ∠3=﹖
什么是三角形的内角和?
1
2
3
一、量一量
测量分工要求:?
1?、 每小组选出锐角三角形、直角三角形、钝角三角形 各两个。每人测量一个。
2、 把角标上序号,量出度数,求出内角和。
3、 汇报给小组长,小组长负责记录。?
4? 、小组长要监督小组其他同学量的是不是很准确、真实,不能改掉小组成员度量出来的数据。??
二、拼一拼
1
2
3
先标出角的序号,再把三个角撕下来
拼成一个角
三角形的内角和
平角:1800
平角:1800
平角:1800
钝角三角形
锐角三角形
直角三角形
折
法国著名的数学家、物理学家。12岁时发现“任意三角形的内角和都是180?”。
布莱士·帕斯卡
(1623—1662)
帕斯卡的验证过程
360°÷ 2 = 180°
直角三角形内角和
180°
180°
180°×2
-180°
=180°
锐角三角形内角和
180°
180°
180°×2-180°=180°
钝角三角形内角和
三、结论
三角形的内角和是180°
?
72°
28°
180°--(72°+28°)=80°
四、练习
猜角
三角形∠1=140°∠3=25°求∠2的度数。
180°-140°-25°
=140°-25°
=15°
180 °-(140° +25°)
=180 °-165°
=15°
猜猜我们多少度?
我是等边三角形,我的一个角多少度?
?度
猜猜我们多少度?
我是等腰直角三角形,我的一个底角多少度?
?度
猜角
如下图,求∠1的度数。
判断
1、三角形越大,内角和越大。
2、一个三角形中最多有一个直角或钝角。
3、两个三角形拼成一个大三角形,这个大三角形的内角和是360 °。
(×)
(√ )
(× )
一个等腰三角形的风筝,它的一个底角是700,它的顶角是多少度?
一个等腰三角形的风筝,它的一个底角是700,它的顶角是多少度?
1800-700×2
=1800 -1400
=400
1800-700 -700
=1100 -700
=400
700
700
400
答:它的顶角是400。
家里镜框上的一块三角形玻璃碎了(如图)。聪明的明明,只带了其中的一块去玻璃店,就配到了和原来一模一样的。你知道他带的是哪一块吗?
知识的升华
你能根据三角形的内角和求出四边形、五边形、六边形的内角和吗?
两个三角形:180°×2=360 °
三个三角形: 180°×3=540 °
4个三角形:180°×4=720°
知识的升华
多边形 边数 三角形个数 多边形的内角和
四边形 4 2 2×180°
五边形 5 3 3 ×180°
六边形 6 4 4 ×180°
七边形
知识的升华
多边形 边数 三角形个数 多边形的内角和
四边形 4 2 2×180°
五边形 5 3 3 ×180°
六边形 6 4 4 ×180°
七边形 7 5
n边形
知识的升华
多边形 边数 三角形个数 多边形的内角和
四边形 4 2 2×180°
五边形 5 3 3 ×180°
六边形 6 4 4 ×180°
七边形 7 5 5 ×180°
n边形
知识的升华
多边形 边数 三角形个数 多边形的内角和
四边形 4 2 2×180°
五边形 5 3 3 ×180°
六边形 6 4 4 ×180°
七边形 7 5 5 ×180°
n边形 n n-2
知识的升华
多边形 边数 三角形个数 多边形的内角和
四边形 4 2 2×180°
五边形 5 3 3 ×180°
六边形 6 4 4 ×180°
七边形 7 5 5 ×180°
N边形 n n-2
知识的升华
多边形 边数 三角形个数 多边形的内角和
四边形 4 2 2×180°
五边形 5 3 3 ×180°
六边形 6 4 4 ×180°
七边形 7 5 5 ×180°
n边形 n n-2 (n-2)×180°
知识的升华
多边形 边数 三角形个数 多边形的内角和
四边形 4 2
(边数-2)×180°
五边形 5 3
六边形 6 4
七边形 7 5
n边形 n n-2
