高中物理选修3-5动量守恒定律单元测试PDF版含答案
文档属性
| 名称 | 高中物理选修3-5动量守恒定律单元测试PDF版含答案 |  | |
| 格式 | zip | ||
| 文件大小 | 555.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(新课程标准) | ||
| 科目 | 物理 | ||
| 更新时间 | 2020-02-13 17:52:23 | ||
图片预览




文档简介
高中物理选修 3.5 动量守恒定律单元测试
一.选择题(共 10 小题)
1.在滑冰场上,甲、乙两小孩分别坐在滑冰板上,原来静止不动,在相互猛推一下后分别
向相反方向运动,甲在冰上滑行的距离比乙远。假定两板与冰面间的动摩擦因数相同,
下列判断正确的是( )
A.在推的过程中,甲推乙的力小于乙推甲的力
B.在推的过程中,甲推乙的时间小于乙推甲的时间
C.在分开时,甲的运动速度大于乙的运动速度
D.在分开后,甲运动的加速度大小小于乙运动的加速度大小
2.A、B 两物块沿同一直线运动,发生碰撞后结合在一起,碰撞前后的 x﹣t 图象如图所示,
其中 a、b 分别为 A、B 碰前的图象,c 为碰后的图象。则 A、B 两物块质量之比为( )
A.2:3 B.1:4 C.3:2 D.4:3
3.如图所示,光滑的四分之一圆弧轨道 M 静止在光滑水平面上,一个物块 m 在水平地面
上以大小为 v0 的初速度向右运动并无能量损失地滑上圆弧轨道,当物块运动到圆弧轨道
上某一位置时,物块向上的速度为零,此时物块与圆弧轨道的动能之比为 1:2,则此时
物块的动能与重力势能之比为(以地面为零势能面)( )
A.1:2 B.1:3 C.1:6 D.1:9
4.假设一小型宇宙飞船沿人造卫星的轨道在高空做匀速圆周运动,运动周期为 T,如果飞
船沿与其速度相反的方向抛出一个物体 A,以后的运动可能是( )
A.物体 A 与飞船运动周期都等于 T
B.物体 A 的运动周期等于 T,而飞船的运动周期小于 T
C.物体 A 竖直下落,而飞船在原轨道上运动
D.物体 A 和飞船的运动周期都大于 T
5.忽然“唵﹣﹣”的一声,一辆运沙车按着大喇叭轰隆隆的从旁边开过,小明就想,装沙
时运沙车都是停在沙场传送带下,等装满沙后再开走,为了提高效率,他觉得应该让运
沙车边走边装沙。设想运沙车沿着固定的水平轨道向前行驶,沙子从传送带上匀速地竖
直漏下,已知某时刻运沙车前进的速度为 v,单位时间从传送带上漏下的沙子质量为 m,
则下列说法中正确的是( )
A.若轨道光滑,则运沙车和漏进车的沙组成的系统动量守恒
B.若轨道光滑,则运沙车装的沙越来越多,速度却能保持不变
C.已知此时运沙车所受的轨道阻力为 F 阻,则要维持运沙车匀速前进,运沙车的牵引力
应为 F=F 阻
D.已知此时运沙车所受的轨道阻力为 F 阻,则要维持运沙车匀速前进,运沙车的牵引力
应为 F=F 阻+mv
6.若物体在运动过程中,受到的合外力不为零,那么以下说法正确的是( )
A.物体的动能一定变化
B.物体的动量一定变化
C.物体的速度大小和方向一定都变化
D.物体的加速度一定变化
7.“跳马”是集技术、力量、勇气于一体的高难度竞技体操项目。运动员完成空中动作落地
时,通常要下蹲后再站起。这样做是为了( )
A.增大运动员的动量变化量
B.减小运动员的动量变化量
C.减小运动员的动量变化率
D.增大地面对运动员的冲量
8.鸟撞飞机是导致空难的重要因素之一。假设在某次空难中,鸟的质量为 0.8kg,飞行的速
度为 7m/s,迎面撞上速度为 480km/h 的飞机,鸟撞飞机的作用时间大约为 7.5×10﹣5s,
对飞机的撞击力约为( )
A.1.34×105N B.1.49×106N C.1.34×106N D.1.49×105N
9.民航客机飞行过程中遭遇鸟击容易造成重大事故。若一飞机以 150m/s 的速度飞行时,机
头遭到一质量约为 0.2kg、身长约为 8﹣10cm 的飞鸟迎头撞击,飞鸟在空中的飞行速度与
飞机相比可忽略,则飞机受到飞鸟对它的平均作用力的大小约为( )
A.5×103N B.5×104N C.5x105 N D.5×106N
10.一质量为 m 的运动员托着质量为 M 的重物从下蹲状态(图甲)缓慢运动到站立状态(图
乙),该过程重物和人的肩部相对位置不变。运动员保持乙状态站立△t 时间后再将重物
缓慢向上举,至双臂伸直(图丙)。甲到乙、乙到丙过程重物上升高度分别为 h1,h2,经
历的时间分别为 t1、t2,则下面说法中正确的是( )
A.地面对运动员的冲量为(M+m)g(t1+t2+△t),地面对运动员做的功为(M+m)g(h1+h2)
B.地面对运动员的冲量为(M+m)g(t1+t2+△t),地面对运动员做的功为 0
C.运动员对重物的冲量为 0,运动员对重物做的功为 Mg(h1+h2)
D.运动员对重物的冲量为 Mg(t1+t2),运动员对重物做的功为 0
二.填空题(共 5 小题)
11.碰撞问题中,内力远大于外力,往往认为动量守恒,则:
(1)若两物体发生一维碰撞,质量分别为 m1 和 m2,碰前速度分别为 v1 和 v2,碰后速
度分别为 v1'和 v2',动量守恒的表达式为: 。
(2)根据机械能是否守恒,可以判断碰撞时弹性碰撞还是非弹性碰撞,那么:
①弹性碰撞中 = 成立(用(1)中字母表示)。
②非弹性碰撞中 > 成立(用(1)中字母表示)。
③完全非弹性碰撞最显著的特征是 (用(1)中字母表示)。
12.如图所示,木块 A 的质量 mA=1kg,足够长的木板 B 的质量 mB=4kg,质量为 mC=4kg
的木块 C 置于木板 B 上,水平面光滑,B、C 之间有摩擦。现使 A 以 v0=12m/s 的初速
度向右运动,与 B 碰撞后以 4m/s 的速度弹回,则 A 与 B 碰撞后瞬间,B 的速度为
m/s,C 运动过程中的最大速度为 m/s,整个过程中因为 B、C 之间的摩擦而产生
的总内能为 J。
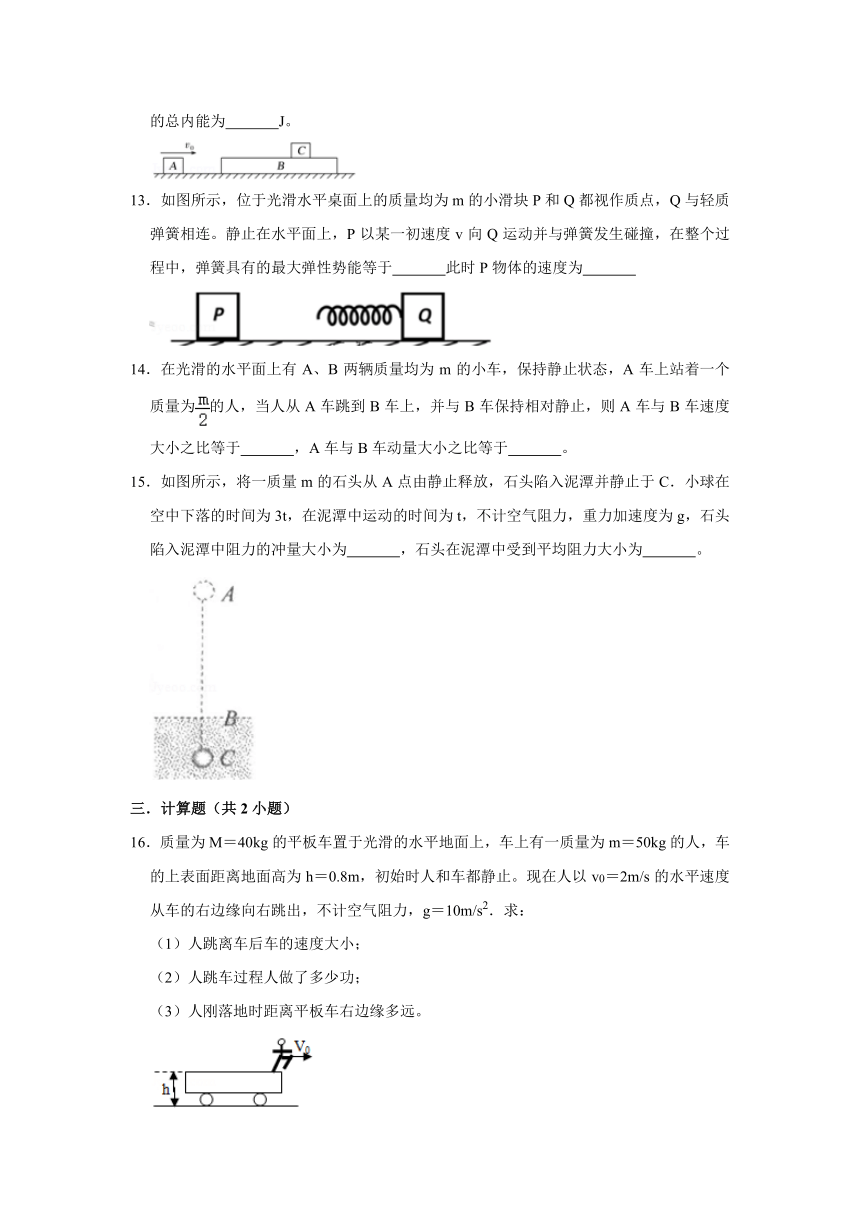
13.如图所示,位于光滑水平桌面上的质量均为 m 的小滑块 P 和 Q 都视作质点,Q 与轻质
弹簧相连。静止在水平面上,P 以某一初速度 v 向 Q 运动并与弹簧发生碰撞,在整个过
程中,弹簧具有的最大弹性势能等于 此时 P 物体的速度为
14.在光滑的水平面上有 A、B 两辆质量均为 m 的小车,保持静止状态,A 车上站着一个
质量为 的人,当人从 A 车跳到 B 车上,并与 B 车保持相对静止,则 A 车与 B 车速度
大小之比等于 ,A 车与 B 车动量大小之比等于 。
15.如图所示,将一质量 m 的石头从 A 点由静止释放,石头陷入泥潭并静止于 C.小球在
空中下落的时间为 3t,在泥潭中运动的时间为 t,不计空气阻力,重力加速度为 g,石头
陷入泥潭中阻力的冲量大小为 ,石头在泥潭中受到平均阻力大小为 。
三.计算题(共 2 小题)
16.质量为 M=40kg 的平板车置于光滑的水平地面上,车上有一质量为 m=50kg 的人,车
的上表面距离地面高为 h=0.8m,初始时人和车都静止。现在人以 v0=2m/s 的水平速度
从车的右边缘向右跳出,不计空气阻力,g=10m/s2.求:
(1)人跳离车后车的速度大小;
(2)人跳车过程人做了多少功;
(3)人刚落地时距离平板车右边缘多远。
17.如图所示,物块 B 静止在水平面上,物块 A 以大小为 v0 的速度水平向右正对 B 物块运
动并与之发生弹性碰撞,碰撞时间很短可不计,碰撞后 B 物块运动 2m 的位移停止。已
知 A、B 两物块质量分别为 mA=1kg,mB=4kg,两物块与水平面的滑动摩擦系数均为 μ
=0.4,两物块可视为质点,重力加速度 g=10m/s2.求:
(1)碰撞前瞬间 A 物块的速度大小 v0;
(2)最终 A、B 物块间的距离。
参考答案与试题解析
一.选择题(共 10 小题)
1.在滑冰场上,甲、乙两小孩分别坐在滑冰板上,原来静止不动,在相互猛推一下后分别
向相反方向运动,甲在冰上滑行的距离比乙远。假定两板与冰面间的动摩擦因数相同,
下列判断正确的是( )
A.在推的过程中,甲推乙的力小于乙推甲的力
B.在推的过程中,甲推乙的时间小于乙推甲的时间
C.在分开时,甲的运动速度大于乙的运动速度
D.在分开后,甲运动的加速度大小小于乙运动的加速度大小
【分析】作用力和反作用力一定是两个物体之间的相互作用力,并且大小相等,方向相
反,同时产生同时消失。根据牛顿第二定律和运动学公式分析求解。
【解答】解:A、作用力和反作用力一定是两个物体之间的相互作用力,并且大小相等,
在推的过程中,甲的推力等于乙的推力,故 A 错误;
B、作用力和反作用力同时产生同时消失。甲推的乙的时间等于乙推甲的时间,故 B 错
误;
D、由于两板与冰面间的摩擦因数相同,由牛顿第二定律可以知道,μmg=ma,所以 a=
μg,即他们的加速度的大小是相同的,故 D 错误;
C、由于甲在冰上滑行的距离比乙远,根据 V2=2ax 可知,在刚分开时,甲的初速度大于
乙的初速度,故 C 正确。
故选:C。
2.A、B 两物块沿同一直线运动,发生碰撞后结合在一起,碰撞前后的 x﹣t 图象如图所示,
其中 a、b 分别为 A、B 碰前的图象,c 为碰后的图象。则 A、B 两物块质量之比为( )
A.2:3 B.1:4 C.3:2 D.4:3
【分析】在位移时间图象中,斜率表示物体的速度,由图象可知碰撞前后的速度,根据
动量守恒定律可以求出 A、B 球的质量关系。
【解答】解:由图示图象可知,碰撞前,B 球的速度:vA= m/s=﹣3m/s,B 球的
速度为:vB= m/s=2m/s
碰撞后,A、B 两球的速度相等,为:vA′=vB′=v= m/s=﹣1m/s
A、B 组成的系统动量守恒,以碰撞前 B 的速度方向为正方向,由动量守恒定律得:
mAvA+mBvB=(mA+mB)v
代入数据解得: ,故 ABD 错误,C 正确。
故选:C。
3.如图所示,光滑的四分之一圆弧轨道 M 静止在光滑水平面上,一个物块 m 在水平地面
上以大小为 v0 的初速度向右运动并无能量损失地滑上圆弧轨道,当物块运动到圆弧轨道
上某一位置时,物块向上的速度为零,此时物块与圆弧轨道的动能之比为 1:2,则此时
物块的动能与重力势能之比为(以地面为零势能面)( )
A.1:2 B.1:3 C.1:6 D.1:9
【分析】根据题意判断动量是否守恒,当向上速度为零,两物体共速,根据题意求出质
量之比,再根据动量守恒和能量守恒求出物块的动能和势能之比。
【解答】解:因为水平面光滑,m 和 M 看做系统水平方向动量守恒;
当物块向上的速度为零,根据题意可知此时两物体速度相同
又因为此时物块与圆弧轨道的动能之比为 1:2 即 : =1:2
得到 m:M=1:2
根据动量守恒定律:mv0=(m+M)v
得到:v0=3v
根据能量守恒定律:
解得:
此时物块的动能为 Ek=
所以此时物块的动能与重力势能之比为 1:6,故 C 正确,ABD 错误
故选:C。
4.假设一小型宇宙飞船沿人造卫星的轨道在高空做匀速圆周运动,运动周期为 T,如果飞
船沿与其速度相反的方向抛出一个物体 A,以后的运动可能是( )
A.物体 A 与飞船运动周期都等于 T
B.物体 A 的运动周期等于 T,而飞船的运动周期小于 T
C.物体 A 竖直下落,而飞船在原轨道上运动
D.物体 A 和飞船的运动周期都大于 T
【分析】整个过程中系统动量守恒,而抛出后 A 的速度方向有几种可能,根据抛出后 A
的速度的大小和方向结合向心力的知识判断 A 物体的运动情况。
【解答】解:ABC、飞船沿与其速度相反的方向发射一个物体 A 的过程,飞船与 A 组成
的系统动量守恒,因为物体 A 是沿飞船向后抛出,由动量守恒定律可知,飞船的动量一
定增大,飞船的速度增大,根据万有引力提供向心力的特点可知,飞船将做离心运动,
上升到高轨道,飞船的轨道半径 r 飞船变大,飞船不可能在原轨道运动,由 T=2π 可
知,飞船的周期 T 变大,故 ABC 都错误;
D、抛出后物体的速度方向有几种可能:
①若抛出后物体的速度方向与飞船方向相同,则物体 A 的速度减小,将做近心运动,rA
变小,由 T=2π 可知,A 的周期变小,小于 T;
②若抛出后物体的速度为零,则 A 会在万有引力的作用下竖直下落。
③若物体的速度方向与飞船方向相反,其大小可能等于飞船原来的速度,此时仍将在原
轨道运行,rA 不变,由 T=2π 可知可知,A 的周期不变,等于 T;
④A 的速度也可能大于飞船原来的速度,此时也将上升到高轨道运动,rA 变大,由由 T
=2π 可知,A 的周期变大,大于 T;
由以上分析,故 D 正确;
故选:D。
5.忽然“唵﹣﹣”的一声,一辆运沙车按着大喇叭轰隆隆的从旁边开过,小明就想,装沙
时运沙车都是停在沙场传送带下,等装满沙后再开走,为了提高效率,他觉得应该让运
沙车边走边装沙。设想运沙车沿着固定的水平轨道向前行驶,沙子从传送带上匀速地竖
直漏下,已知某时刻运沙车前进的速度为 v,单位时间从传送带上漏下的沙子质量为 m,
则下列说法中正确的是( )
A.若轨道光滑,则运沙车和漏进车的沙组成的系统动量守恒
B.若轨道光滑,则运沙车装的沙越来越多,速度却能保持不变
C.已知此时运沙车所受的轨道阻力为 F 阻,则要维持运沙车匀速前进,运沙车的牵引力
应为 F=F 阻
D.已知此时运沙车所受的轨道阻力为 F 阻,则要维持运沙车匀速前进,运沙车的牵引力
应为 F=F 阻+mv
【分析】根据系统水平方向动量守恒定律分析沙车速度的变化;选一段极短时间△t 内漏
进沙车的沙子△m 为研究对象,由动量定理得车对漏进来的沙子向前的作用力,以沙车
为研究对象根据平衡条件即可求解运沙车的牵引力。
【解答】解:A、若轨道光滑,则运沙车和漏进车的沙组成的系统水平方向动量守恒,而
不是总动量守恒,因为沙子的竖直动量在变化,故 A 错误;
B、设某时刻沙车总质量为 M,随后一段时间△t 内漏进沙车的沙子质量为△m,则由水
平方向动量守恒,有 Mv+0=(M+△m)v′,可以看出沙车速度会逐渐减小,故 B 错误;
C、选一段极短时间△t 内漏进沙车的沙子△m 为研究对象,由动量定理,有 F△t=△mv
﹣0,得车对漏进来的沙子向前的作用力为 =mv,则以沙车为研究对象,由平
衡条件,有 ,其中 F′是漏进沙子对车的阻力,由牛顿第三定律有 F′
=F,联立得 ,故 C 错误,D 正确;
故选:D。
6.若物体在运动过程中,受到的合外力不为零,那么以下说法正确的是( )
A.物体的动能一定变化
B.物体的动量一定变化
C.物体的速度大小和方向一定都变化
D.物体的加速度一定变化
【分析】物体在运动过程中所受到的合外力不为零,根据合力是否做功,分析动能是否
变化。根据牛顿第二定律分析加速度和速度是否变化,根据动量定理分析动量的变化。
【解答】解:AC、物体在运动过程中所受到的合外力不为零,若合力总与速度垂直,合
力不做功,由动能定理得知物体的动能不变,比如匀速圆周运动,则速度大小不变,方
向变化,故 AC 错误。
B、由于合外力不为零,则合外力的冲量不为零,故物体的动量一定变化,故 B 正确。
D、物体在运动过程中所受到的合外力不为零,合力可能不变,如匀变速直线运动;也可
能变,如匀速圆周运动;故加速度可能不变,也可能变,故 D 错误。
故选:B。
7.“跳马”是集技术、力量、勇气于一体的高难度竞技体操项目。运动员完成空中动作落地
时,通常要下蹲后再站起。这样做是为了( )
A.增大运动员的动量变化量
B.减小运动员的动量变化量
C.减小运动员的动量变化率
D.增大地面对运动员的冲量
【分析】运动员在脚接触地面后都有一个下蹲的过程,为的是减小地面对人的冲击力。
运动员的动量变化量不变,根据动量定理分析。
【解答】解:运动员完成空中动作落地时,通常要下蹲后再站起。延长了作用时间,根
据动量定理可知,Ft=△p,
运动员的动量变化量不变,则地面对运动员的冲量不变,延长作用时间 t,减小了地面对
运动员的冲力,F= ,即减小了运动员的动量变化率,故 C 正确,ABD 错误。
故选:C。
8.鸟撞飞机是导致空难的重要因素之一。假设在某次空难中,鸟的质量为 0.8kg,飞行的速
度为 7m/s,迎面撞上速度为 480km/h 的飞机,鸟撞飞机的作用时间大约为 7.5×10﹣5s,
对飞机的撞击力约为( )
A.1.34×105N B.1.49×106N C.1.34×106N D.1.49×105N
【分析】对小鸟进行分析,碰撞过程由动量定理进行分析即可求得撞击力。
【解答】解:480km/h=133.3m/s,
研究小鸟的受力情况,规定初速度为正,由动量定理有:
Ft=m△v,
得:F= = N=﹣1.49×106N,
负号表示撞击力与鸟的初速度方向相反,故 B 正确,ACD 错误。
故选:B。
9.民航客机飞行过程中遭遇鸟击容易造成重大事故。若一飞机以 150m/s 的速度飞行时,机
头遭到一质量约为 0.2kg、身长约为 8﹣10cm 的飞鸟迎头撞击,飞鸟在空中的飞行速度与
飞机相比可忽略,则飞机受到飞鸟对它的平均作用力的大小约为( )
A.5×103N B.5×104N C.5x105 N D.5×106N
【分析】应用动量定理可以求出撞击时受到的平均撞击力。
【解答】解:本题为估算题,可以认为撞击前鸟的速度为零,撞击后鸟与飞机的速度相
等,飞机速度为:v=150m/s,
撞击的时间约为 t= s=6×10﹣4s
撞击过程可以认为鸟做匀加速直线运动,对鸟,由动量定理得:Ft=mv﹣0
F= = N=5×104N,故 ACD 错误,B 正确;
故选:B。
10.一质量为 m 的运动员托着质量为 M 的重物从下蹲状态(图甲)缓慢运动到站立状态(图
乙),该过程重物和人的肩部相对位置不变。运动员保持乙状态站立△t 时间后再将重物
缓慢向上举,至双臂伸直(图丙)。甲到乙、乙到丙过程重物上升高度分别为 h1,h2,经
历的时间分别为 t1、t2,则下面说法中正确的是( )
A.地面对运动员的冲量为(M+m)g(t1+t2+△t),地面对运动员做的功为(M+m)g(h1+h2)
B.地面对运动员的冲量为(M+m)g(t1+t2+△t),地面对运动员做的功为 0
C.运动员对重物的冲量为 0,运动员对重物做的功为 Mg(h1+h2)
D.运动员对重物的冲量为 Mg(t1+t2),运动员对重物做的功为 0
【分析】由力的冲量的定义求冲量值,由 W=Fs 求功。
【解答】解:AB、因缓慢运动,则为平衡状态,则地面对运动员的力为(M+m)g,作
用时间为(t1+t2+△t),则其冲量为 I=(M+m)g(t1+t2+△t),
因地面对运动员的力的作用点没有位移,则地面对运动员做的功为 0,故 B 正确,A 错
误;
CD、运动员对重物的力为 Mg,其冲量为 I′=Mg(t1+t2+△t),运动员对重物力作用下
的位移为(h1+h2),则对重物做功为 Mg(h1+h2),故 CD 错误。
故选:B。
二.填空题(共 5 小题)
11.碰撞问题中,内力远大于外力,往往认为动量守恒,则:
(1)若两物体发生一维碰撞,质量分别为 m1 和 m2,碰前速度分别为 v1 和 v2,碰后速
度分别为 v1'和 v2',动量守恒的表达式为: m1v1+m2v2=m1v1'+m2v2' 。
(2)根据机械能是否守恒,可以判断碰撞时弹性碰撞还是非弹性碰撞,那么:
①弹性碰撞中 m1v12+ m2v22 = m1v1'2+ m2v2'2 成立(用(1)中字母表示)。
②非弹性碰撞中 m1v12+ m2v22 > m1v1'2+ m2v2'2 成立(用(1)中字母表示)。
③完全非弹性碰撞最显著的特征是 v1'=v2' (用(1)中字母表示)。
【分析】(1)碰撞过程系统动量守恒,碰撞前后系统总动量保持不变,根据题意求出动
量守恒的表达式。
(2)①弹性碰撞过程机械能守恒;
②非弹性碰撞过程机械能不守恒,机械能有损失;
③完全非弹性碰撞后两物体速度相等。
【解答】解:(1)系统内力远大于外力,系统动量守恒,以碰撞前 m1 的速度方向为正方
向,
由动量守恒定律得:m1v1+m2v2=m1v1'+m2v2';
(2)①弹性碰撞过程系统机械能守恒,即: m1v12+ m2v22= m1v1'2+ m2v2'2;
②非弹性碰撞过程系统机械能有损失,碰撞后机械能减少,即: m1v12+ m2v22>
m1v1'2+ m2v2'2;
③完全非弹性碰撞后两物体结合在一起,碰撞后两者速度相等,即:v1'=v2';
故答案为:(1)m1v1+m2v2=m1v1'+m2v2';(2)① m1v12+ m2v22; m1v1'2+ m2v2'2;
② m1v12+ m2v22; m1v1'2+ m2v2'2;③v1'=v2'。
12.如图所示,木块 A 的质量 mA=1kg,足够长的木板 B 的质量 mB=4kg,质量为 mC=4kg
的木块 C 置于木板 B 上,水平面光滑,B、C 之间有摩擦。现使 A 以 v0=12m/s 的初速
度向右运动,与B碰撞后以 4m/s的速度弹回,则A与B碰撞后瞬间,B的速度为 4 m/s,
C 运动过程中的最大速度为 2 m/s,整个过程中因为 B、C 之间的摩擦而产生的总内能
为 16 J。
【分析】A 与 B 碰后的瞬间,B 的速度最大,以 A、B 为系统,运用动量守恒定律求出 B
运动过程中的速度;
碰撞后 C 在 B 上滑行一段距离后与 B 保持相对静止,两者速度相同,此时 C 的速度最大,
由动量守恒定律可以求出 C 的最大速度;
应用能量守恒定律可以求出因摩擦产生的内能。
【解答】解:A 与 B 碰后瞬间,C 的运动状态未变,B 速度最大。
A、B 系统动量守恒,取向右为正方向,由动量守恒定律得:
mAv0=﹣mAvA+mBvB,代入数据得:vB=4m/s;
B 与 C 相互作用使 B 减速、C 加速,由于 B 板足够长,所以 B 和 C 能达到相同速度,
二者共速后,C 速度最大,B、C 系统动量守恒,以 B 的速度方向为正方向,
由动量守恒定律得:mBvB=(mB+mC)vC,代入数据得:vC=2m/s;
对 B、C 系统,由能量守恒定律得: ,
代入数据解得:Q=16J;
故答案为:4;2;16。
13.如图所示,位于光滑水平桌面上的质量均为 m 的小滑块 P 和 Q 都视作质点,Q 与轻质
弹簧相连。静止在水平面上,P 以某一初速度 v 向 Q 运动并与弹簧发生碰撞,在整个过
程中,弹簧具有的最大弹性势能等于 mv2 此时 P 物体的速度为 v
【分析】当 P、Q 速度相等时,弹簧的弹性势能最大,根据动量守恒定律求此时物体 P
的速度,根据系统的机械能守恒求出弹簧的最大弹性势能。
【解答】解:P、Q 相互作用过程系统动量守恒,当两者速度相同时弹簧的弹性势能最大,
以 P 的初速度方向为正方向,由动量守恒定律得:mv=(m+m)v1
解得
由能量守恒定律得
解得:
故答案为: mv2, v。
14.在光滑的水平面上有 A、B 两辆质量均为 m 的小车,保持静止状态,A 车上站着一个
质量为 的人,当人从 A 车跳到 B 车上,并与 B 车保持相对静止,则 A 车与 B 车速度
大小之比等于 3:2 ,A 车与 B 车动量大小之比等于 3:2 。
【分析】对人以及两车组成的系统研究,该系统在整个过程中动量守恒。根据动量守恒
定律求出 A 车与 B 车速度大小之比以及 A 车和 B 车的动量大小之比。
【解答】解:对人、A、B 两车组成的系统,取 A 车的速度方向为正方向,由动量守恒
定律得:0=mvA﹣(m+ )vB。
可知:vA:vB=3:2。
A 车的动量大小 pA=mvA,B 车的动量大小 pB=mvB,
则 pA:pB=3:2
故答案为:3:2;3:2。
15.如图所示,将一质量 m 的石头从 A 点由静止释放,石头陷入泥潭并静止于 C.小球在
空中下落的时间为 3t,在泥潭中运动的时间为 t,不计空气阻力,重力加速度为 g,石头
陷入泥潭中阻力的冲量大小为 4mgt ,石头在泥潭中受到平均阻力大小为 4mg 。
【分析】全过程根据动量定理求解阻力的冲量,根据冲量的计算公式求解阻力。
【解答】解:设阻力的冲量为 I,全过程根据动量定理可得:
mg?4t﹣I=0
解得:I=4mgt
根据冲量的计算公式可得:I=ft,
解得:f=4mg。
故答案为:4mgt,4mg。
三.计算题(共 2 小题)
16.质量为 M=40kg 的平板车置于光滑的水平地面上,车上有一质量为 m=50kg 的人,车
的上表面距离地面高为 h=0.8m,初始时人和车都静止。现在人以 v0=2m/s 的水平速度
从车的右边缘向右跳出,不计空气阻力,g=10m/s2.求:
(1)人跳离车后车的速度大小;
(2)人跳车过程人做了多少功;
(3)人刚落地时距离平板车右边缘多远。
【分析】(1)对人和车分析,根据动量守恒定律即可求出人跳离车后车的速度;
(2)根据功能关系即可确定人做的功;
(3)人跳离车后做平抛运动,根据平抛运动规律即可求出人离车的距离。
【解答】解:(1)人和车水平方向动量守恒,设人跳出的方向为正方向,则有:
mv0=Mv1
解得车获得的速度为:v1=2.5m/s;
(2)根据功能关系可知,人做的功等于人和车动能的增加量,则有:
W= Mv12+ mv02
解得 W=225J;
(3)人离开小车后做平抛运动,
竖直方向 h= gt2
解得:t=0.4s
人落地时距离车右端 s=(v0+v1)t=(2.5+0.4)×0.4m=1.8m。
答:(1)人跳离车后车的速度大小为 2.5m/s;
(2)人跳车过程人做了 225J 的功;
(3)人刚落地时距离平板车右边缘 1.8m。
17.如图所示,物块 B 静止在水平面上,物块 A 以大小为 v0 的速度水平向右正对 B 物块运
动并与之发生弹性碰撞,碰撞时间很短可不计,碰撞后 B 物块运动 2m 的位移停止。已
知 A、B 两物块质量分别为 mA=1kg,mB=4kg,两物块与水平面的滑动摩擦系数均为 μ
=0.4,两物块可视为质点,重力加速度 g=10m/s2.求:
(1)碰撞前瞬间 A 物块的速度大小 v0;
(2)最终 A、B 物块间的距离。
【分析】(1)由动能定理求出碰撞后 B 的速度;碰撞过程中 AB 系统动量守恒,机械能
也守恒,由此即可求出碰撞前瞬间 A 物块的速度大小 v0 以及碰撞后 A 的速度;
(2)根据动能定理求出 A 的位移,然后由空间关系求出最终 A、B 物块间的距离。
【解答】解:(1)设碰撞后 A 的速度为 v1,B 的速度为 v2,选择向右为正方向,A 与 B
发生弹性正碰过程中系统的动量守恒,得:mAv0=mAv1+mBv2
由机械能守恒得:
B 向右运动的过程中克服摩擦力做功,则有:
联立解得:v0=10m/s,v1=﹣6m/s,负号表示 A 向左运动;
(2)A 向左运动的过程中克服摩擦力做功,则有:
代入数据可得:xA=4.5m
则 AB 之间的距离为:L=xA+xB=4.5m+2m=6.5m
答:(1)碰撞前瞬间 A 物块的速度大小为 10m/s。
(2)最终 A、B 物块间的距离为 6.5m。
一.选择题(共 10 小题)
1.在滑冰场上,甲、乙两小孩分别坐在滑冰板上,原来静止不动,在相互猛推一下后分别
向相反方向运动,甲在冰上滑行的距离比乙远。假定两板与冰面间的动摩擦因数相同,
下列判断正确的是( )
A.在推的过程中,甲推乙的力小于乙推甲的力
B.在推的过程中,甲推乙的时间小于乙推甲的时间
C.在分开时,甲的运动速度大于乙的运动速度
D.在分开后,甲运动的加速度大小小于乙运动的加速度大小
2.A、B 两物块沿同一直线运动,发生碰撞后结合在一起,碰撞前后的 x﹣t 图象如图所示,
其中 a、b 分别为 A、B 碰前的图象,c 为碰后的图象。则 A、B 两物块质量之比为( )
A.2:3 B.1:4 C.3:2 D.4:3
3.如图所示,光滑的四分之一圆弧轨道 M 静止在光滑水平面上,一个物块 m 在水平地面
上以大小为 v0 的初速度向右运动并无能量损失地滑上圆弧轨道,当物块运动到圆弧轨道
上某一位置时,物块向上的速度为零,此时物块与圆弧轨道的动能之比为 1:2,则此时
物块的动能与重力势能之比为(以地面为零势能面)( )
A.1:2 B.1:3 C.1:6 D.1:9
4.假设一小型宇宙飞船沿人造卫星的轨道在高空做匀速圆周运动,运动周期为 T,如果飞
船沿与其速度相反的方向抛出一个物体 A,以后的运动可能是( )
A.物体 A 与飞船运动周期都等于 T
B.物体 A 的运动周期等于 T,而飞船的运动周期小于 T
C.物体 A 竖直下落,而飞船在原轨道上运动
D.物体 A 和飞船的运动周期都大于 T
5.忽然“唵﹣﹣”的一声,一辆运沙车按着大喇叭轰隆隆的从旁边开过,小明就想,装沙
时运沙车都是停在沙场传送带下,等装满沙后再开走,为了提高效率,他觉得应该让运
沙车边走边装沙。设想运沙车沿着固定的水平轨道向前行驶,沙子从传送带上匀速地竖
直漏下,已知某时刻运沙车前进的速度为 v,单位时间从传送带上漏下的沙子质量为 m,
则下列说法中正确的是( )
A.若轨道光滑,则运沙车和漏进车的沙组成的系统动量守恒
B.若轨道光滑,则运沙车装的沙越来越多,速度却能保持不变
C.已知此时运沙车所受的轨道阻力为 F 阻,则要维持运沙车匀速前进,运沙车的牵引力
应为 F=F 阻
D.已知此时运沙车所受的轨道阻力为 F 阻,则要维持运沙车匀速前进,运沙车的牵引力
应为 F=F 阻+mv
6.若物体在运动过程中,受到的合外力不为零,那么以下说法正确的是( )
A.物体的动能一定变化
B.物体的动量一定变化
C.物体的速度大小和方向一定都变化
D.物体的加速度一定变化
7.“跳马”是集技术、力量、勇气于一体的高难度竞技体操项目。运动员完成空中动作落地
时,通常要下蹲后再站起。这样做是为了( )
A.增大运动员的动量变化量
B.减小运动员的动量变化量
C.减小运动员的动量变化率
D.增大地面对运动员的冲量
8.鸟撞飞机是导致空难的重要因素之一。假设在某次空难中,鸟的质量为 0.8kg,飞行的速
度为 7m/s,迎面撞上速度为 480km/h 的飞机,鸟撞飞机的作用时间大约为 7.5×10﹣5s,
对飞机的撞击力约为( )
A.1.34×105N B.1.49×106N C.1.34×106N D.1.49×105N
9.民航客机飞行过程中遭遇鸟击容易造成重大事故。若一飞机以 150m/s 的速度飞行时,机
头遭到一质量约为 0.2kg、身长约为 8﹣10cm 的飞鸟迎头撞击,飞鸟在空中的飞行速度与
飞机相比可忽略,则飞机受到飞鸟对它的平均作用力的大小约为( )
A.5×103N B.5×104N C.5x105 N D.5×106N
10.一质量为 m 的运动员托着质量为 M 的重物从下蹲状态(图甲)缓慢运动到站立状态(图
乙),该过程重物和人的肩部相对位置不变。运动员保持乙状态站立△t 时间后再将重物
缓慢向上举,至双臂伸直(图丙)。甲到乙、乙到丙过程重物上升高度分别为 h1,h2,经
历的时间分别为 t1、t2,则下面说法中正确的是( )
A.地面对运动员的冲量为(M+m)g(t1+t2+△t),地面对运动员做的功为(M+m)g(h1+h2)
B.地面对运动员的冲量为(M+m)g(t1+t2+△t),地面对运动员做的功为 0
C.运动员对重物的冲量为 0,运动员对重物做的功为 Mg(h1+h2)
D.运动员对重物的冲量为 Mg(t1+t2),运动员对重物做的功为 0
二.填空题(共 5 小题)
11.碰撞问题中,内力远大于外力,往往认为动量守恒,则:
(1)若两物体发生一维碰撞,质量分别为 m1 和 m2,碰前速度分别为 v1 和 v2,碰后速
度分别为 v1'和 v2',动量守恒的表达式为: 。
(2)根据机械能是否守恒,可以判断碰撞时弹性碰撞还是非弹性碰撞,那么:
①弹性碰撞中 = 成立(用(1)中字母表示)。
②非弹性碰撞中 > 成立(用(1)中字母表示)。
③完全非弹性碰撞最显著的特征是 (用(1)中字母表示)。
12.如图所示,木块 A 的质量 mA=1kg,足够长的木板 B 的质量 mB=4kg,质量为 mC=4kg
的木块 C 置于木板 B 上,水平面光滑,B、C 之间有摩擦。现使 A 以 v0=12m/s 的初速
度向右运动,与 B 碰撞后以 4m/s 的速度弹回,则 A 与 B 碰撞后瞬间,B 的速度为
m/s,C 运动过程中的最大速度为 m/s,整个过程中因为 B、C 之间的摩擦而产生
的总内能为 J。
13.如图所示,位于光滑水平桌面上的质量均为 m 的小滑块 P 和 Q 都视作质点,Q 与轻质
弹簧相连。静止在水平面上,P 以某一初速度 v 向 Q 运动并与弹簧发生碰撞,在整个过
程中,弹簧具有的最大弹性势能等于 此时 P 物体的速度为
14.在光滑的水平面上有 A、B 两辆质量均为 m 的小车,保持静止状态,A 车上站着一个
质量为 的人,当人从 A 车跳到 B 车上,并与 B 车保持相对静止,则 A 车与 B 车速度
大小之比等于 ,A 车与 B 车动量大小之比等于 。
15.如图所示,将一质量 m 的石头从 A 点由静止释放,石头陷入泥潭并静止于 C.小球在
空中下落的时间为 3t,在泥潭中运动的时间为 t,不计空气阻力,重力加速度为 g,石头
陷入泥潭中阻力的冲量大小为 ,石头在泥潭中受到平均阻力大小为 。
三.计算题(共 2 小题)
16.质量为 M=40kg 的平板车置于光滑的水平地面上,车上有一质量为 m=50kg 的人,车
的上表面距离地面高为 h=0.8m,初始时人和车都静止。现在人以 v0=2m/s 的水平速度
从车的右边缘向右跳出,不计空气阻力,g=10m/s2.求:
(1)人跳离车后车的速度大小;
(2)人跳车过程人做了多少功;
(3)人刚落地时距离平板车右边缘多远。
17.如图所示,物块 B 静止在水平面上,物块 A 以大小为 v0 的速度水平向右正对 B 物块运
动并与之发生弹性碰撞,碰撞时间很短可不计,碰撞后 B 物块运动 2m 的位移停止。已
知 A、B 两物块质量分别为 mA=1kg,mB=4kg,两物块与水平面的滑动摩擦系数均为 μ
=0.4,两物块可视为质点,重力加速度 g=10m/s2.求:
(1)碰撞前瞬间 A 物块的速度大小 v0;
(2)最终 A、B 物块间的距离。
参考答案与试题解析
一.选择题(共 10 小题)
1.在滑冰场上,甲、乙两小孩分别坐在滑冰板上,原来静止不动,在相互猛推一下后分别
向相反方向运动,甲在冰上滑行的距离比乙远。假定两板与冰面间的动摩擦因数相同,
下列判断正确的是( )
A.在推的过程中,甲推乙的力小于乙推甲的力
B.在推的过程中,甲推乙的时间小于乙推甲的时间
C.在分开时,甲的运动速度大于乙的运动速度
D.在分开后,甲运动的加速度大小小于乙运动的加速度大小
【分析】作用力和反作用力一定是两个物体之间的相互作用力,并且大小相等,方向相
反,同时产生同时消失。根据牛顿第二定律和运动学公式分析求解。
【解答】解:A、作用力和反作用力一定是两个物体之间的相互作用力,并且大小相等,
在推的过程中,甲的推力等于乙的推力,故 A 错误;
B、作用力和反作用力同时产生同时消失。甲推的乙的时间等于乙推甲的时间,故 B 错
误;
D、由于两板与冰面间的摩擦因数相同,由牛顿第二定律可以知道,μmg=ma,所以 a=
μg,即他们的加速度的大小是相同的,故 D 错误;
C、由于甲在冰上滑行的距离比乙远,根据 V2=2ax 可知,在刚分开时,甲的初速度大于
乙的初速度,故 C 正确。
故选:C。
2.A、B 两物块沿同一直线运动,发生碰撞后结合在一起,碰撞前后的 x﹣t 图象如图所示,
其中 a、b 分别为 A、B 碰前的图象,c 为碰后的图象。则 A、B 两物块质量之比为( )
A.2:3 B.1:4 C.3:2 D.4:3
【分析】在位移时间图象中,斜率表示物体的速度,由图象可知碰撞前后的速度,根据
动量守恒定律可以求出 A、B 球的质量关系。
【解答】解:由图示图象可知,碰撞前,B 球的速度:vA= m/s=﹣3m/s,B 球的
速度为:vB= m/s=2m/s
碰撞后,A、B 两球的速度相等,为:vA′=vB′=v= m/s=﹣1m/s
A、B 组成的系统动量守恒,以碰撞前 B 的速度方向为正方向,由动量守恒定律得:
mAvA+mBvB=(mA+mB)v
代入数据解得: ,故 ABD 错误,C 正确。
故选:C。
3.如图所示,光滑的四分之一圆弧轨道 M 静止在光滑水平面上,一个物块 m 在水平地面
上以大小为 v0 的初速度向右运动并无能量损失地滑上圆弧轨道,当物块运动到圆弧轨道
上某一位置时,物块向上的速度为零,此时物块与圆弧轨道的动能之比为 1:2,则此时
物块的动能与重力势能之比为(以地面为零势能面)( )
A.1:2 B.1:3 C.1:6 D.1:9
【分析】根据题意判断动量是否守恒,当向上速度为零,两物体共速,根据题意求出质
量之比,再根据动量守恒和能量守恒求出物块的动能和势能之比。
【解答】解:因为水平面光滑,m 和 M 看做系统水平方向动量守恒;
当物块向上的速度为零,根据题意可知此时两物体速度相同
又因为此时物块与圆弧轨道的动能之比为 1:2 即 : =1:2
得到 m:M=1:2
根据动量守恒定律:mv0=(m+M)v
得到:v0=3v
根据能量守恒定律:
解得:
此时物块的动能为 Ek=
所以此时物块的动能与重力势能之比为 1:6,故 C 正确,ABD 错误
故选:C。
4.假设一小型宇宙飞船沿人造卫星的轨道在高空做匀速圆周运动,运动周期为 T,如果飞
船沿与其速度相反的方向抛出一个物体 A,以后的运动可能是( )
A.物体 A 与飞船运动周期都等于 T
B.物体 A 的运动周期等于 T,而飞船的运动周期小于 T
C.物体 A 竖直下落,而飞船在原轨道上运动
D.物体 A 和飞船的运动周期都大于 T
【分析】整个过程中系统动量守恒,而抛出后 A 的速度方向有几种可能,根据抛出后 A
的速度的大小和方向结合向心力的知识判断 A 物体的运动情况。
【解答】解:ABC、飞船沿与其速度相反的方向发射一个物体 A 的过程,飞船与 A 组成
的系统动量守恒,因为物体 A 是沿飞船向后抛出,由动量守恒定律可知,飞船的动量一
定增大,飞船的速度增大,根据万有引力提供向心力的特点可知,飞船将做离心运动,
上升到高轨道,飞船的轨道半径 r 飞船变大,飞船不可能在原轨道运动,由 T=2π 可
知,飞船的周期 T 变大,故 ABC 都错误;
D、抛出后物体的速度方向有几种可能:
①若抛出后物体的速度方向与飞船方向相同,则物体 A 的速度减小,将做近心运动,rA
变小,由 T=2π 可知,A 的周期变小,小于 T;
②若抛出后物体的速度为零,则 A 会在万有引力的作用下竖直下落。
③若物体的速度方向与飞船方向相反,其大小可能等于飞船原来的速度,此时仍将在原
轨道运行,rA 不变,由 T=2π 可知可知,A 的周期不变,等于 T;
④A 的速度也可能大于飞船原来的速度,此时也将上升到高轨道运动,rA 变大,由由 T
=2π 可知,A 的周期变大,大于 T;
由以上分析,故 D 正确;
故选:D。
5.忽然“唵﹣﹣”的一声,一辆运沙车按着大喇叭轰隆隆的从旁边开过,小明就想,装沙
时运沙车都是停在沙场传送带下,等装满沙后再开走,为了提高效率,他觉得应该让运
沙车边走边装沙。设想运沙车沿着固定的水平轨道向前行驶,沙子从传送带上匀速地竖
直漏下,已知某时刻运沙车前进的速度为 v,单位时间从传送带上漏下的沙子质量为 m,
则下列说法中正确的是( )
A.若轨道光滑,则运沙车和漏进车的沙组成的系统动量守恒
B.若轨道光滑,则运沙车装的沙越来越多,速度却能保持不变
C.已知此时运沙车所受的轨道阻力为 F 阻,则要维持运沙车匀速前进,运沙车的牵引力
应为 F=F 阻
D.已知此时运沙车所受的轨道阻力为 F 阻,则要维持运沙车匀速前进,运沙车的牵引力
应为 F=F 阻+mv
【分析】根据系统水平方向动量守恒定律分析沙车速度的变化;选一段极短时间△t 内漏
进沙车的沙子△m 为研究对象,由动量定理得车对漏进来的沙子向前的作用力,以沙车
为研究对象根据平衡条件即可求解运沙车的牵引力。
【解答】解:A、若轨道光滑,则运沙车和漏进车的沙组成的系统水平方向动量守恒,而
不是总动量守恒,因为沙子的竖直动量在变化,故 A 错误;
B、设某时刻沙车总质量为 M,随后一段时间△t 内漏进沙车的沙子质量为△m,则由水
平方向动量守恒,有 Mv+0=(M+△m)v′,可以看出沙车速度会逐渐减小,故 B 错误;
C、选一段极短时间△t 内漏进沙车的沙子△m 为研究对象,由动量定理,有 F△t=△mv
﹣0,得车对漏进来的沙子向前的作用力为 =mv,则以沙车为研究对象,由平
衡条件,有 ,其中 F′是漏进沙子对车的阻力,由牛顿第三定律有 F′
=F,联立得 ,故 C 错误,D 正确;
故选:D。
6.若物体在运动过程中,受到的合外力不为零,那么以下说法正确的是( )
A.物体的动能一定变化
B.物体的动量一定变化
C.物体的速度大小和方向一定都变化
D.物体的加速度一定变化
【分析】物体在运动过程中所受到的合外力不为零,根据合力是否做功,分析动能是否
变化。根据牛顿第二定律分析加速度和速度是否变化,根据动量定理分析动量的变化。
【解答】解:AC、物体在运动过程中所受到的合外力不为零,若合力总与速度垂直,合
力不做功,由动能定理得知物体的动能不变,比如匀速圆周运动,则速度大小不变,方
向变化,故 AC 错误。
B、由于合外力不为零,则合外力的冲量不为零,故物体的动量一定变化,故 B 正确。
D、物体在运动过程中所受到的合外力不为零,合力可能不变,如匀变速直线运动;也可
能变,如匀速圆周运动;故加速度可能不变,也可能变,故 D 错误。
故选:B。
7.“跳马”是集技术、力量、勇气于一体的高难度竞技体操项目。运动员完成空中动作落地
时,通常要下蹲后再站起。这样做是为了( )
A.增大运动员的动量变化量
B.减小运动员的动量变化量
C.减小运动员的动量变化率
D.增大地面对运动员的冲量
【分析】运动员在脚接触地面后都有一个下蹲的过程,为的是减小地面对人的冲击力。
运动员的动量变化量不变,根据动量定理分析。
【解答】解:运动员完成空中动作落地时,通常要下蹲后再站起。延长了作用时间,根
据动量定理可知,Ft=△p,
运动员的动量变化量不变,则地面对运动员的冲量不变,延长作用时间 t,减小了地面对
运动员的冲力,F= ,即减小了运动员的动量变化率,故 C 正确,ABD 错误。
故选:C。
8.鸟撞飞机是导致空难的重要因素之一。假设在某次空难中,鸟的质量为 0.8kg,飞行的速
度为 7m/s,迎面撞上速度为 480km/h 的飞机,鸟撞飞机的作用时间大约为 7.5×10﹣5s,
对飞机的撞击力约为( )
A.1.34×105N B.1.49×106N C.1.34×106N D.1.49×105N
【分析】对小鸟进行分析,碰撞过程由动量定理进行分析即可求得撞击力。
【解答】解:480km/h=133.3m/s,
研究小鸟的受力情况,规定初速度为正,由动量定理有:
Ft=m△v,
得:F= = N=﹣1.49×106N,
负号表示撞击力与鸟的初速度方向相反,故 B 正确,ACD 错误。
故选:B。
9.民航客机飞行过程中遭遇鸟击容易造成重大事故。若一飞机以 150m/s 的速度飞行时,机
头遭到一质量约为 0.2kg、身长约为 8﹣10cm 的飞鸟迎头撞击,飞鸟在空中的飞行速度与
飞机相比可忽略,则飞机受到飞鸟对它的平均作用力的大小约为( )
A.5×103N B.5×104N C.5x105 N D.5×106N
【分析】应用动量定理可以求出撞击时受到的平均撞击力。
【解答】解:本题为估算题,可以认为撞击前鸟的速度为零,撞击后鸟与飞机的速度相
等,飞机速度为:v=150m/s,
撞击的时间约为 t= s=6×10﹣4s
撞击过程可以认为鸟做匀加速直线运动,对鸟,由动量定理得:Ft=mv﹣0
F= = N=5×104N,故 ACD 错误,B 正确;
故选:B。
10.一质量为 m 的运动员托着质量为 M 的重物从下蹲状态(图甲)缓慢运动到站立状态(图
乙),该过程重物和人的肩部相对位置不变。运动员保持乙状态站立△t 时间后再将重物
缓慢向上举,至双臂伸直(图丙)。甲到乙、乙到丙过程重物上升高度分别为 h1,h2,经
历的时间分别为 t1、t2,则下面说法中正确的是( )
A.地面对运动员的冲量为(M+m)g(t1+t2+△t),地面对运动员做的功为(M+m)g(h1+h2)
B.地面对运动员的冲量为(M+m)g(t1+t2+△t),地面对运动员做的功为 0
C.运动员对重物的冲量为 0,运动员对重物做的功为 Mg(h1+h2)
D.运动员对重物的冲量为 Mg(t1+t2),运动员对重物做的功为 0
【分析】由力的冲量的定义求冲量值,由 W=Fs 求功。
【解答】解:AB、因缓慢运动,则为平衡状态,则地面对运动员的力为(M+m)g,作
用时间为(t1+t2+△t),则其冲量为 I=(M+m)g(t1+t2+△t),
因地面对运动员的力的作用点没有位移,则地面对运动员做的功为 0,故 B 正确,A 错
误;
CD、运动员对重物的力为 Mg,其冲量为 I′=Mg(t1+t2+△t),运动员对重物力作用下
的位移为(h1+h2),则对重物做功为 Mg(h1+h2),故 CD 错误。
故选:B。
二.填空题(共 5 小题)
11.碰撞问题中,内力远大于外力,往往认为动量守恒,则:
(1)若两物体发生一维碰撞,质量分别为 m1 和 m2,碰前速度分别为 v1 和 v2,碰后速
度分别为 v1'和 v2',动量守恒的表达式为: m1v1+m2v2=m1v1'+m2v2' 。
(2)根据机械能是否守恒,可以判断碰撞时弹性碰撞还是非弹性碰撞,那么:
①弹性碰撞中 m1v12+ m2v22 = m1v1'2+ m2v2'2 成立(用(1)中字母表示)。
②非弹性碰撞中 m1v12+ m2v22 > m1v1'2+ m2v2'2 成立(用(1)中字母表示)。
③完全非弹性碰撞最显著的特征是 v1'=v2' (用(1)中字母表示)。
【分析】(1)碰撞过程系统动量守恒,碰撞前后系统总动量保持不变,根据题意求出动
量守恒的表达式。
(2)①弹性碰撞过程机械能守恒;
②非弹性碰撞过程机械能不守恒,机械能有损失;
③完全非弹性碰撞后两物体速度相等。
【解答】解:(1)系统内力远大于外力,系统动量守恒,以碰撞前 m1 的速度方向为正方
向,
由动量守恒定律得:m1v1+m2v2=m1v1'+m2v2';
(2)①弹性碰撞过程系统机械能守恒,即: m1v12+ m2v22= m1v1'2+ m2v2'2;
②非弹性碰撞过程系统机械能有损失,碰撞后机械能减少,即: m1v12+ m2v22>
m1v1'2+ m2v2'2;
③完全非弹性碰撞后两物体结合在一起,碰撞后两者速度相等,即:v1'=v2';
故答案为:(1)m1v1+m2v2=m1v1'+m2v2';(2)① m1v12+ m2v22; m1v1'2+ m2v2'2;
② m1v12+ m2v22; m1v1'2+ m2v2'2;③v1'=v2'。
12.如图所示,木块 A 的质量 mA=1kg,足够长的木板 B 的质量 mB=4kg,质量为 mC=4kg
的木块 C 置于木板 B 上,水平面光滑,B、C 之间有摩擦。现使 A 以 v0=12m/s 的初速
度向右运动,与B碰撞后以 4m/s的速度弹回,则A与B碰撞后瞬间,B的速度为 4 m/s,
C 运动过程中的最大速度为 2 m/s,整个过程中因为 B、C 之间的摩擦而产生的总内能
为 16 J。
【分析】A 与 B 碰后的瞬间,B 的速度最大,以 A、B 为系统,运用动量守恒定律求出 B
运动过程中的速度;
碰撞后 C 在 B 上滑行一段距离后与 B 保持相对静止,两者速度相同,此时 C 的速度最大,
由动量守恒定律可以求出 C 的最大速度;
应用能量守恒定律可以求出因摩擦产生的内能。
【解答】解:A 与 B 碰后瞬间,C 的运动状态未变,B 速度最大。
A、B 系统动量守恒,取向右为正方向,由动量守恒定律得:
mAv0=﹣mAvA+mBvB,代入数据得:vB=4m/s;
B 与 C 相互作用使 B 减速、C 加速,由于 B 板足够长,所以 B 和 C 能达到相同速度,
二者共速后,C 速度最大,B、C 系统动量守恒,以 B 的速度方向为正方向,
由动量守恒定律得:mBvB=(mB+mC)vC,代入数据得:vC=2m/s;
对 B、C 系统,由能量守恒定律得: ,
代入数据解得:Q=16J;
故答案为:4;2;16。
13.如图所示,位于光滑水平桌面上的质量均为 m 的小滑块 P 和 Q 都视作质点,Q 与轻质
弹簧相连。静止在水平面上,P 以某一初速度 v 向 Q 运动并与弹簧发生碰撞,在整个过
程中,弹簧具有的最大弹性势能等于 mv2 此时 P 物体的速度为 v
【分析】当 P、Q 速度相等时,弹簧的弹性势能最大,根据动量守恒定律求此时物体 P
的速度,根据系统的机械能守恒求出弹簧的最大弹性势能。
【解答】解:P、Q 相互作用过程系统动量守恒,当两者速度相同时弹簧的弹性势能最大,
以 P 的初速度方向为正方向,由动量守恒定律得:mv=(m+m)v1
解得
由能量守恒定律得
解得:
故答案为: mv2, v。
14.在光滑的水平面上有 A、B 两辆质量均为 m 的小车,保持静止状态,A 车上站着一个
质量为 的人,当人从 A 车跳到 B 车上,并与 B 车保持相对静止,则 A 车与 B 车速度
大小之比等于 3:2 ,A 车与 B 车动量大小之比等于 3:2 。
【分析】对人以及两车组成的系统研究,该系统在整个过程中动量守恒。根据动量守恒
定律求出 A 车与 B 车速度大小之比以及 A 车和 B 车的动量大小之比。
【解答】解:对人、A、B 两车组成的系统,取 A 车的速度方向为正方向,由动量守恒
定律得:0=mvA﹣(m+ )vB。
可知:vA:vB=3:2。
A 车的动量大小 pA=mvA,B 车的动量大小 pB=mvB,
则 pA:pB=3:2
故答案为:3:2;3:2。
15.如图所示,将一质量 m 的石头从 A 点由静止释放,石头陷入泥潭并静止于 C.小球在
空中下落的时间为 3t,在泥潭中运动的时间为 t,不计空气阻力,重力加速度为 g,石头
陷入泥潭中阻力的冲量大小为 4mgt ,石头在泥潭中受到平均阻力大小为 4mg 。
【分析】全过程根据动量定理求解阻力的冲量,根据冲量的计算公式求解阻力。
【解答】解:设阻力的冲量为 I,全过程根据动量定理可得:
mg?4t﹣I=0
解得:I=4mgt
根据冲量的计算公式可得:I=ft,
解得:f=4mg。
故答案为:4mgt,4mg。
三.计算题(共 2 小题)
16.质量为 M=40kg 的平板车置于光滑的水平地面上,车上有一质量为 m=50kg 的人,车
的上表面距离地面高为 h=0.8m,初始时人和车都静止。现在人以 v0=2m/s 的水平速度
从车的右边缘向右跳出,不计空气阻力,g=10m/s2.求:
(1)人跳离车后车的速度大小;
(2)人跳车过程人做了多少功;
(3)人刚落地时距离平板车右边缘多远。
【分析】(1)对人和车分析,根据动量守恒定律即可求出人跳离车后车的速度;
(2)根据功能关系即可确定人做的功;
(3)人跳离车后做平抛运动,根据平抛运动规律即可求出人离车的距离。
【解答】解:(1)人和车水平方向动量守恒,设人跳出的方向为正方向,则有:
mv0=Mv1
解得车获得的速度为:v1=2.5m/s;
(2)根据功能关系可知,人做的功等于人和车动能的增加量,则有:
W= Mv12+ mv02
解得 W=225J;
(3)人离开小车后做平抛运动,
竖直方向 h= gt2
解得:t=0.4s
人落地时距离车右端 s=(v0+v1)t=(2.5+0.4)×0.4m=1.8m。
答:(1)人跳离车后车的速度大小为 2.5m/s;
(2)人跳车过程人做了 225J 的功;
(3)人刚落地时距离平板车右边缘 1.8m。
17.如图所示,物块 B 静止在水平面上,物块 A 以大小为 v0 的速度水平向右正对 B 物块运
动并与之发生弹性碰撞,碰撞时间很短可不计,碰撞后 B 物块运动 2m 的位移停止。已
知 A、B 两物块质量分别为 mA=1kg,mB=4kg,两物块与水平面的滑动摩擦系数均为 μ
=0.4,两物块可视为质点,重力加速度 g=10m/s2.求:
(1)碰撞前瞬间 A 物块的速度大小 v0;
(2)最终 A、B 物块间的距离。
【分析】(1)由动能定理求出碰撞后 B 的速度;碰撞过程中 AB 系统动量守恒,机械能
也守恒,由此即可求出碰撞前瞬间 A 物块的速度大小 v0 以及碰撞后 A 的速度;
(2)根据动能定理求出 A 的位移,然后由空间关系求出最终 A、B 物块间的距离。
【解答】解:(1)设碰撞后 A 的速度为 v1,B 的速度为 v2,选择向右为正方向,A 与 B
发生弹性正碰过程中系统的动量守恒,得:mAv0=mAv1+mBv2
由机械能守恒得:
B 向右运动的过程中克服摩擦力做功,则有:
联立解得:v0=10m/s,v1=﹣6m/s,负号表示 A 向左运动;
(2)A 向左运动的过程中克服摩擦力做功,则有:
代入数据可得:xA=4.5m
则 AB 之间的距离为:L=xA+xB=4.5m+2m=6.5m
答:(1)碰撞前瞬间 A 物块的速度大小为 10m/s。
(2)最终 A、B 物块间的距离为 6.5m。
