1.2 直角三角形的性质和判定(Ⅱ)之勾股定理课件(共20张PPT)
文档属性
| 名称 | 1.2 直角三角形的性质和判定(Ⅱ)之勾股定理课件(共20张PPT) |  | |
| 格式 | zip | ||
| 文件大小 | 1.7MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 湘教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-02-13 19:55:45 | ||
图片预览



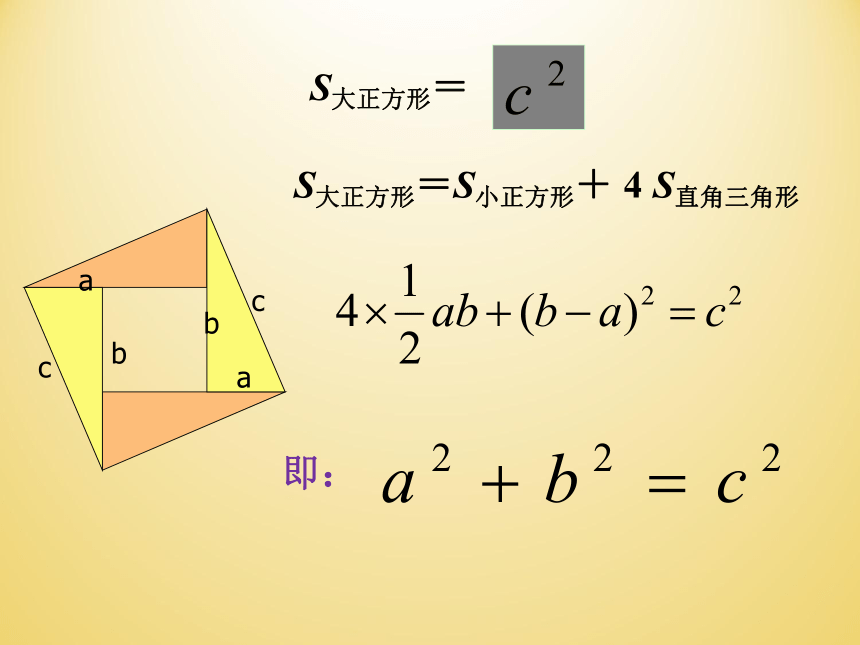
文档简介
(共20张PPT)
勾股定理 (第一课时)
毕达哥拉斯
(公元前572—前497年) 古希腊著名的哲学家、数学家、天文学家.
活动一: 观察猜想
活动二:推理论证
猜想:直角三角形中,两直角边的平方和
等于斜边的平方?
即:
已知:如图,在Rt△ABC中,∠C=90°;
求证:a2 +b2 =c2
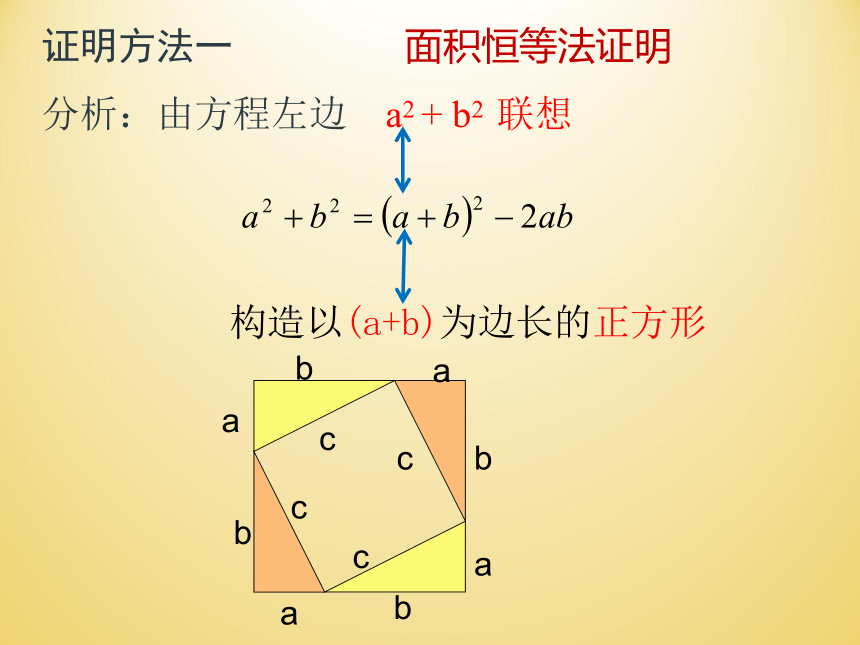
证明方法一 面积恒等法证明
构造以(a+b)为边长的正方形
分析:由方程左边 a2 + b2 联想
c
a
b
c
b
a
a
b
b
a
c
c
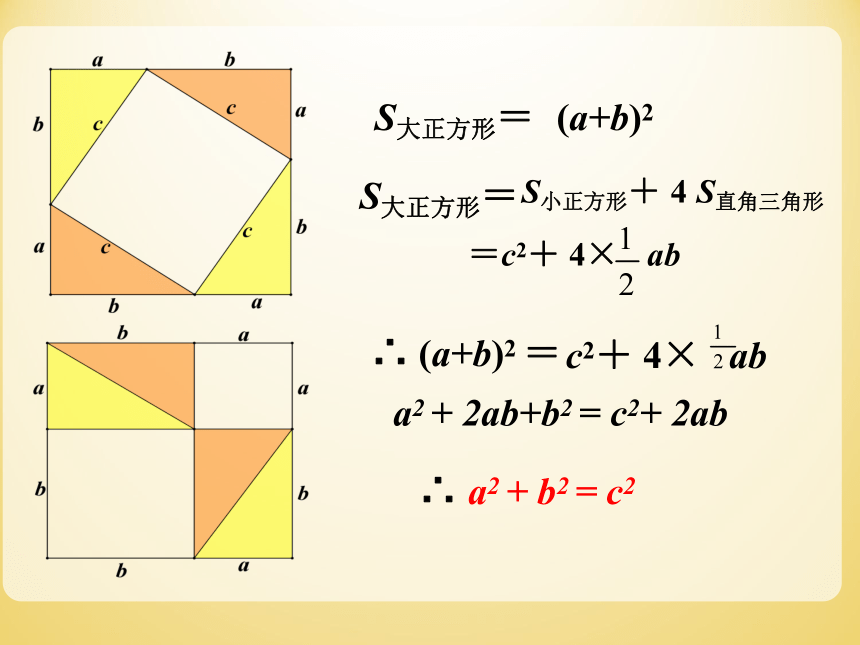
a2 + 2ab+b2 = c2+ 2ab
∴ a2 + b2 = c2
(a+b)2
S小正方形+ 4 S直角三角形
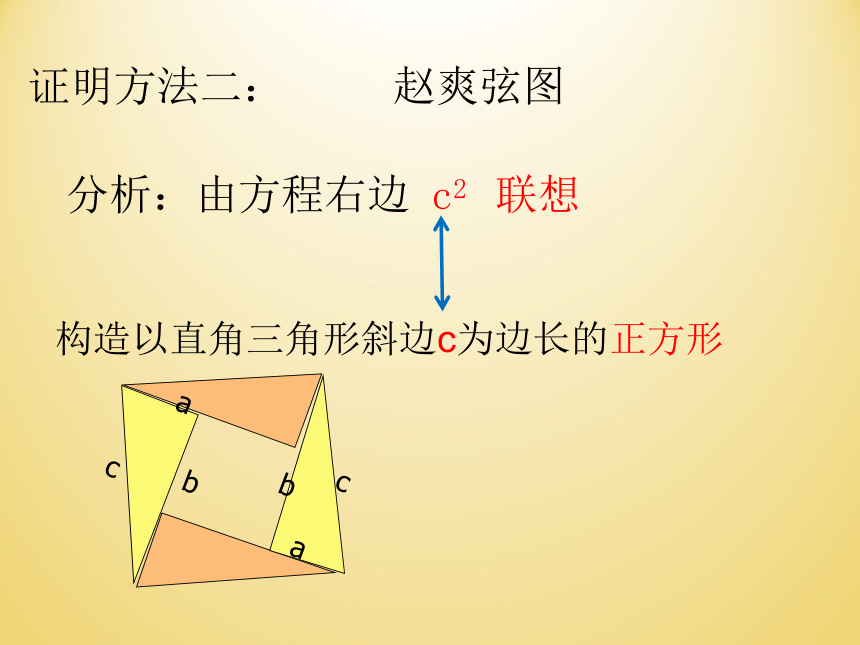
证明方法二: 赵爽弦图
分析:由方程右边 c2 联想
构造以直角三角形斜边c为边长的正方形
即:
S大正方形=
S大正方形=S小正方形+ 4 S直角三角形
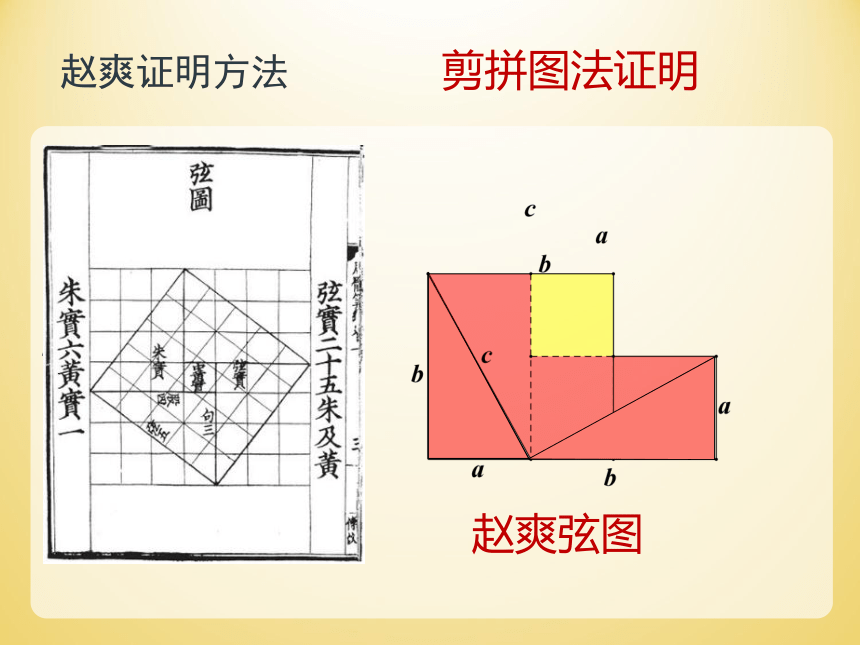
赵爽弦图
赵爽证明方法 剪拼图法证明
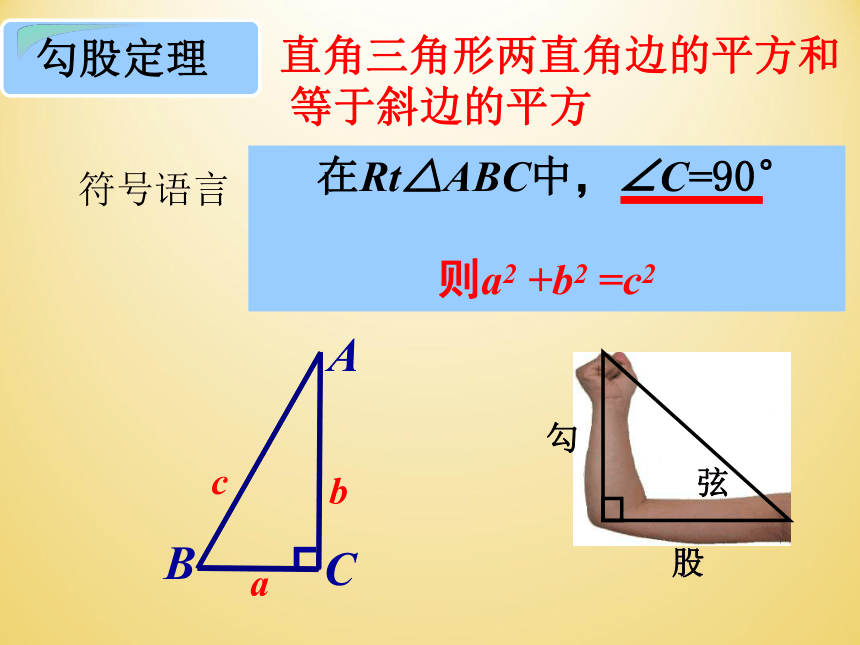
直角三角形两直角边的平方和等于斜边的平方
在Rt△ABC中,∠C=90°
则a2 +b2 =c2
符号语言
弦
学以致用
1. 在RtΔABC中, ∠C = 90?
① 已知a = 3, b = 4, 求c.
② 已知b = 2, c = 4, 求a .
2. 在RtΔABC中, ∠B = 90?, 已知a = 5, b = 13, 求c .
公元前约3000年,古巴比伦人就知道和应用勾股定理,他们还知道许多勾股数组,如3,4,5.
大约公元前2500年,古埃及人在建筑宏伟的金字塔和测量尼罗河泛滥后的土地时,也应用过勾股定理.
大约公元前2000年,大禹在治水的实践中总结出了勾股术,用来确定两处水位的高低差.可以说,禹是世界上有史记载的第一位与勾股定理有关的人.
大约在公元前1100年,周朝数学家商高就提出“勾三、股四、弦五”,记载在《周髀算经》中.
公元前3世纪,古希腊数学家欧几里德巨著《几何原本》中给出一个勾股定理的证明.
公元前5世纪,古希腊数学家毕达哥拉斯就公开发表了这一规律的证明.
公元2世纪的东汉时期,刘徽证明了勾股定理.
大约公元前250年,赵爽对《周髀算经》内的勾股定理作出了详细注释和证明.
2002年在北京召开的国际数学家大会,就以赵爽弦图作为大会会徽的图案.
在探索勾股定理的过程中,你有什么感悟和欣赏.
小结与作业
(1)整理课堂上所提到的勾股定理的证明方法;
(2)教材16页,习题A组第1题;
(3)通过上网等方式查找勾股定理的有关史料、趣事及其他证明方法.
3. 在RtΔABC中,两条边的长度分别是3和 4,
求另一边的长度.
分类讨论
① 斜边=
②直角边=
勾股定理:
如果直角三角形两条直角边长分别为a、b,斜边长为c,那么a2+b2=c2 .
在中国古代,把弯曲成直角的手臂的上半部分称为“勾”,下半部分称为“股”
我国古代学者把直角三角形较短的直角边称为“勾”,较长的直角边称为“股”,斜边称为“弦”
弦
毕达哥拉斯证法
证明方法三
4.如图,图中所有的三角形都是直角三角形,四边形都是正方形.已知正方形A,B,C,D的面积分别是3 ,4,1,3,求最大正方形E的面积.
勾股树
得到半圆A,B,C的面积关系
为SA+SB=SC.
数形结合
放眼未来,华罗庚曾设想:向太空发射一种图形,因为这种图形在几千年前就已经被人类所认识,如果外星人是“文明人”,也必定认识这种图形.
从直角三角形的各边向外作正方形能否推广到从
各边向外作等边三角形(正n边形)吗?
勾股定理 (第一课时)
毕达哥拉斯
(公元前572—前497年) 古希腊著名的哲学家、数学家、天文学家.
活动一: 观察猜想
活动二:推理论证
猜想:直角三角形中,两直角边的平方和
等于斜边的平方?
即:
已知:如图,在Rt△ABC中,∠C=90°;
求证:a2 +b2 =c2
证明方法一 面积恒等法证明
构造以(a+b)为边长的正方形
分析:由方程左边 a2 + b2 联想
c
a
b
c
b
a
a
b
b
a
c
c
a2 + 2ab+b2 = c2+ 2ab
∴ a2 + b2 = c2
(a+b)2
S小正方形+ 4 S直角三角形
证明方法二: 赵爽弦图
分析:由方程右边 c2 联想
构造以直角三角形斜边c为边长的正方形
即:
S大正方形=
S大正方形=S小正方形+ 4 S直角三角形
赵爽弦图
赵爽证明方法 剪拼图法证明
直角三角形两直角边的平方和等于斜边的平方
在Rt△ABC中,∠C=90°
则a2 +b2 =c2
符号语言
弦
学以致用
1. 在RtΔABC中, ∠C = 90?
① 已知a = 3, b = 4, 求c.
② 已知b = 2, c = 4, 求a .
2. 在RtΔABC中, ∠B = 90?, 已知a = 5, b = 13, 求c .
公元前约3000年,古巴比伦人就知道和应用勾股定理,他们还知道许多勾股数组,如3,4,5.
大约公元前2500年,古埃及人在建筑宏伟的金字塔和测量尼罗河泛滥后的土地时,也应用过勾股定理.
大约公元前2000年,大禹在治水的实践中总结出了勾股术,用来确定两处水位的高低差.可以说,禹是世界上有史记载的第一位与勾股定理有关的人.
大约在公元前1100年,周朝数学家商高就提出“勾三、股四、弦五”,记载在《周髀算经》中.
公元前3世纪,古希腊数学家欧几里德巨著《几何原本》中给出一个勾股定理的证明.
公元前5世纪,古希腊数学家毕达哥拉斯就公开发表了这一规律的证明.
公元2世纪的东汉时期,刘徽证明了勾股定理.
大约公元前250年,赵爽对《周髀算经》内的勾股定理作出了详细注释和证明.
2002年在北京召开的国际数学家大会,就以赵爽弦图作为大会会徽的图案.
在探索勾股定理的过程中,你有什么感悟和欣赏.
小结与作业
(1)整理课堂上所提到的勾股定理的证明方法;
(2)教材16页,习题A组第1题;
(3)通过上网等方式查找勾股定理的有关史料、趣事及其他证明方法.
3. 在RtΔABC中,两条边的长度分别是3和 4,
求另一边的长度.
分类讨论
① 斜边=
②直角边=
勾股定理:
如果直角三角形两条直角边长分别为a、b,斜边长为c,那么a2+b2=c2 .
在中国古代,把弯曲成直角的手臂的上半部分称为“勾”,下半部分称为“股”
我国古代学者把直角三角形较短的直角边称为“勾”,较长的直角边称为“股”,斜边称为“弦”
弦
毕达哥拉斯证法
证明方法三
4.如图,图中所有的三角形都是直角三角形,四边形都是正方形.已知正方形A,B,C,D的面积分别是3 ,4,1,3,求最大正方形E的面积.
勾股树
得到半圆A,B,C的面积关系
为SA+SB=SC.
数形结合
放眼未来,华罗庚曾设想:向太空发射一种图形,因为这种图形在几千年前就已经被人类所认识,如果外星人是“文明人”,也必定认识这种图形.
从直角三角形的各边向外作正方形能否推广到从
各边向外作等边三角形(正n边形)吗?
同课章节目录
- 第1章 直角三角形
- 1.1 直角三角形的性质与判定(Ⅰ)
- 1.2 直角三角形的性质与判定(Ⅱ)
- 1.3 直角三角形全等的判定
- 1.4 角平分线的性质
- 第2章 四边形
- 2.1 多边形
- 2.2 平行四边形
- 2.3 中心对称和中心对称图形
- 2.4 三角形的中位线
- 2.5 矩形
- 2.6 菱形
- 2.7 正方形
- 第3章 图形与坐标
- 3.1 平面直角坐标系
- 3.2 简单图形的坐标表示
- 3.3 轴对称和平移的坐标表示
- 第4章 一次函数
- 4.1 函数和它的表示法
- 4.2 一次函数
- 4.3 一次函数的图象
- 4.4 用待定系数法确定一次函数表达式
- 4.5 一次函数的应用
- 第5章 数据的频数分布
- 5.1 频数与频率
- 5.2 频数直方图
