湘教版数学八年级下册:1.2 直角三角形的性质和判定(Ⅱ)勾股定理 课件(共19张PPT)
文档属性
| 名称 | 湘教版数学八年级下册:1.2 直角三角形的性质和判定(Ⅱ)勾股定理 课件(共19张PPT) |
|
|
| 格式 | ppt | ||
| 文件大小 | 1.3MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 湘教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-02-13 00:00:00 | ||
图片预览



文档简介
(共19张PPT)
C
B
A
运动员
悬崖壁
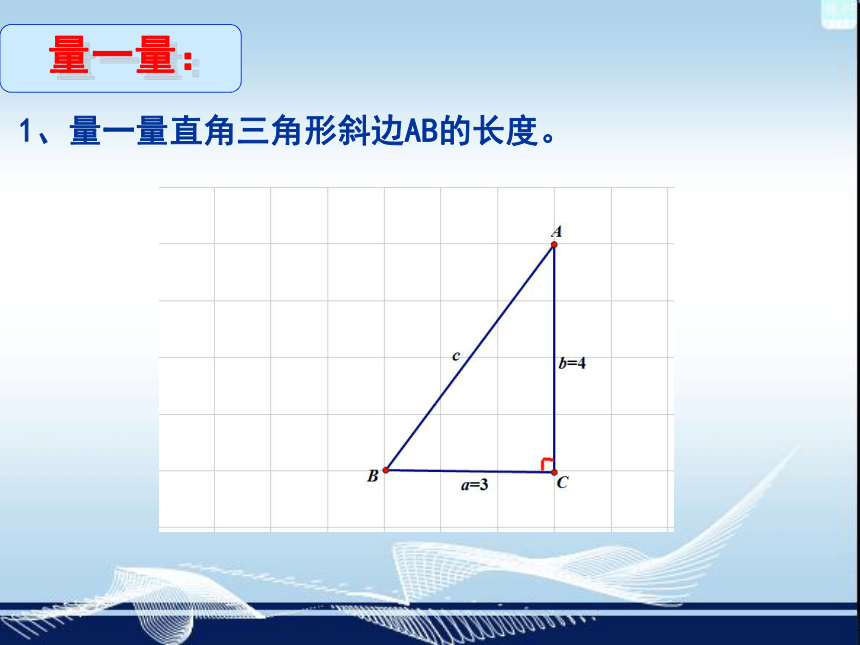
1400米
600米
直角三角形的性质和判定(Ⅱ)
---探索勾股定理
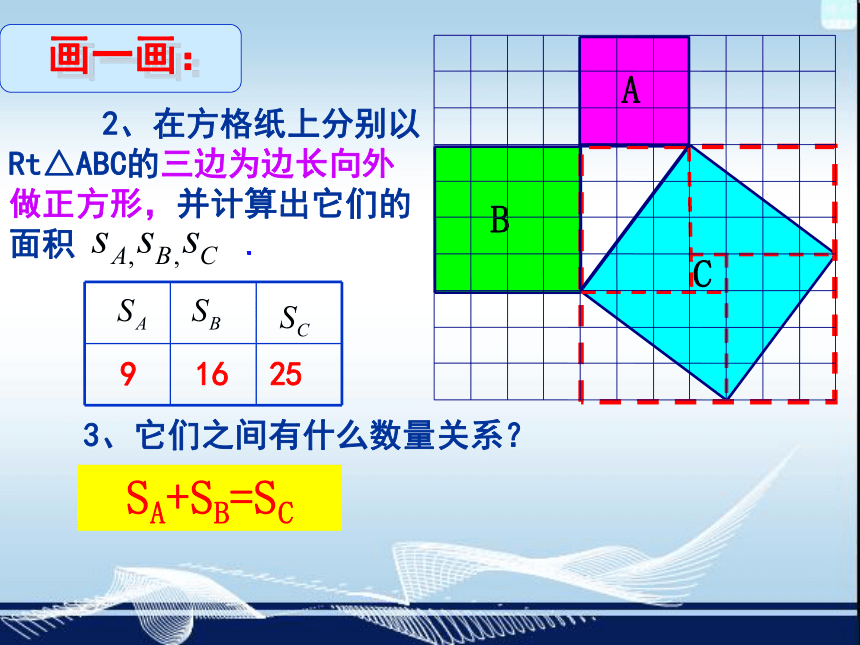
1、量一量直角三角形斜边AB的长度。
量一量:
A
B
C
C
画一画:
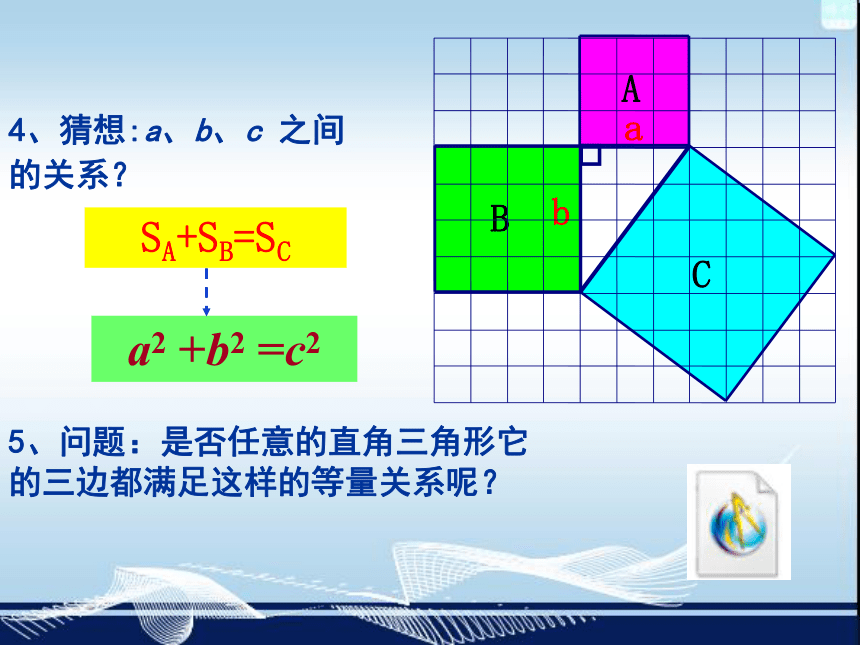
2、在方格纸上分别以Rt△ABC的三边为边长向外做正方形,并计算出它们的面积 .
9
16
25
3、它们之间有什么数量关系?
SA+SB=SC
A
B
SA+SB=SC
a
b
c
C
4、猜想:a、b、c 之间
的关系?
a2 +b2 =c2
5、问题:是否任意的直角三角形它的三边都满足这样的等量关系呢?
1、小组合作:利用你们手中的四个全等的直角三角形拼成一个大正方形。直角三角形的两条直角边分别为a,b(设b>a)斜边为c。
c
a
b
拼一拼:
c
a
b
a
b
c
c
a
b
c
a
b
c
a
b
c
a
b
a
b
c
c
a
b
拼图一
拼图二
c
a
b
c
a
b
c
a
b
a2+2ab+b2 = c2 +2ab
∴a2+b2=c2
大正方形的面积可以表示为________;
也可以表示为___________.
(a+b)2
a
b
c
∵
证一证:
c
a
b
=2ab+b2-2ab+a2
=a2+b2
∴a2+b2=c2
大正方形的面积可以表示为_______;
也可以表示为_______________.
c2
a
b
c
c
a
b
c
a
b
勾股定理
由此得到直角三角形的性质定理:
弦
勾
股
a
c
b
B
C
A
直角三角形两直角边a,b的平方和,等于斜边c的平方.
a2+ b2 = c2
赵爽弦图
早在公元3世纪,我国数学家赵爽就用此图形验证了“勾股定理”。
2002年在北京召开的国际数学家大会会徽
1、判断并说明理由:
1) 直角三角形三边分别为 a, b, c ,则一定满足下面的式子: a +b =c . ( )
2)某△ABC的三边分别是a,b,c,则a = c -b 。
( )
×
×
练一练:
:
C
B
A
运动员
悬崖壁
学以致用:
1400米
600米
在直角三角形中,若已知直角三角形任意两条边长, 我们可以根据勾股定理,求出第三边的长.
A
c2=a2 +b2
a
b
c
b2= c2 - a2
a2= c2 - b2
变式运用:
2、如图,在等腰三角形ABC中,已知AB=AC=13cm,BC=10cm,AD⊥BC于点D.你能算出BC边上的高AD的长吗?
A
C
B
D
3、已知:Rt△ABC中,AC=5,BC=12,则AB的长为________________.
13 或
5
C
A
B
12
5
A
C
B
12
谈谈本节课你的收获
谈一谈:
美国第二十任总统伽菲尔德的证法在数学史上被传为佳话人们为了纪念他对勾股定理直观、简捷、易懂、明了的证明,就把这一证法称为“总统”证法。
有趣的总统证法
C
B
A
运动员
悬崖壁
1400米
600米
直角三角形的性质和判定(Ⅱ)
---探索勾股定理
1、量一量直角三角形斜边AB的长度。
量一量:
A
B
C
C
画一画:
2、在方格纸上分别以Rt△ABC的三边为边长向外做正方形,并计算出它们的面积 .
9
16
25
3、它们之间有什么数量关系?
SA+SB=SC
A
B
SA+SB=SC
a
b
c
C
4、猜想:a、b、c 之间
的关系?
a2 +b2 =c2
5、问题:是否任意的直角三角形它的三边都满足这样的等量关系呢?
1、小组合作:利用你们手中的四个全等的直角三角形拼成一个大正方形。直角三角形的两条直角边分别为a,b(设b>a)斜边为c。
c
a
b
拼一拼:
c
a
b
a
b
c
c
a
b
c
a
b
c
a
b
c
a
b
a
b
c
c
a
b
拼图一
拼图二
c
a
b
c
a
b
c
a
b
a2+2ab+b2 = c2 +2ab
∴a2+b2=c2
大正方形的面积可以表示为________;
也可以表示为___________.
(a+b)2
a
b
c
∵
证一证:
c
a
b
=2ab+b2-2ab+a2
=a2+b2
∴a2+b2=c2
大正方形的面积可以表示为_______;
也可以表示为_______________.
c2
a
b
c
c
a
b
c
a
b
勾股定理
由此得到直角三角形的性质定理:
弦
勾
股
a
c
b
B
C
A
直角三角形两直角边a,b的平方和,等于斜边c的平方.
a2+ b2 = c2
赵爽弦图
早在公元3世纪,我国数学家赵爽就用此图形验证了“勾股定理”。
2002年在北京召开的国际数学家大会会徽
1、判断并说明理由:
1) 直角三角形三边分别为 a, b, c ,则一定满足下面的式子: a +b =c . ( )
2)某△ABC的三边分别是a,b,c,则a = c -b 。
( )
×
×
练一练:
:
C
B
A
运动员
悬崖壁
学以致用:
1400米
600米
在直角三角形中,若已知直角三角形任意两条边长, 我们可以根据勾股定理,求出第三边的长.
A
c2=a2 +b2
a
b
c
b2= c2 - a2
a2= c2 - b2
变式运用:
2、如图,在等腰三角形ABC中,已知AB=AC=13cm,BC=10cm,AD⊥BC于点D.你能算出BC边上的高AD的长吗?
A
C
B
D
3、已知:Rt△ABC中,AC=5,BC=12,则AB的长为________________.
13 或
5
C
A
B
12
5
A
C
B
12
谈谈本节课你的收获
谈一谈:
美国第二十任总统伽菲尔德的证法在数学史上被传为佳话人们为了纪念他对勾股定理直观、简捷、易懂、明了的证明,就把这一证法称为“总统”证法。
有趣的总统证法
同课章节目录
- 第1章 直角三角形
- 1.1 直角三角形的性质与判定(Ⅰ)
- 1.2 直角三角形的性质与判定(Ⅱ)
- 1.3 直角三角形全等的判定
- 1.4 角平分线的性质
- 第2章 四边形
- 2.1 多边形
- 2.2 平行四边形
- 2.3 中心对称和中心对称图形
- 2.4 三角形的中位线
- 2.5 矩形
- 2.6 菱形
- 2.7 正方形
- 第3章 图形与坐标
- 3.1 平面直角坐标系
- 3.2 简单图形的坐标表示
- 3.3 轴对称和平移的坐标表示
- 第4章 一次函数
- 4.1 函数和它的表示法
- 4.2 一次函数
- 4.3 一次函数的图象
- 4.4 用待定系数法确定一次函数表达式
- 4.5 一次函数的应用
- 第5章 数据的频数分布
- 5.1 频数与频率
- 5.2 频数直方图
