湘教版九年级数学上册第4章《锐角三角函数》单元测试(有答案)
文档属性
| 名称 | 湘教版九年级数学上册第4章《锐角三角函数》单元测试(有答案) |

|
|
| 格式 | zip | ||
| 文件大小 | 414.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 湘教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-02-13 00:00:00 | ||
图片预览


文档简介
第4章《锐角三角函数》
一.选择题(共10小题,每小题3分,共30分)
1.如图,在Rt△ABC中,∠C=90°,如果∠A=α,AB=5,那么AC等于( )
A.5 B.5 C.5 D.
A.5 B.5 C.5 D.
2.如图,△ABC中,∠C=90°,BC=2,AB=3,则下列结论正确的是( )
A.sinA= B.cosA= C.sinA= D.tanA=
3.在Rt△ABC中,各边都扩大5倍,则∠A的三角函数值( )
A.不变 B.扩大5倍 C.缩小5倍 D.不能确定
4.当锐角A的cosA>时,∠A的值为( )
A.小于45° B.小于30° C.大于45° D.大于30°
5.在Rt△ABC中,∠C=90°,若cosA=,则sinA的值为( )
A. B. C. D.
6.在Rt△ABC中,∠C=90°,cosA=,则sinB的值为( )
A. B. C. D.2
7.如果,那么锐角α的度数是( )
A.30° B.45° C.60° D.90°
8.△ABC中,∠A,∠B都是锐角,且sinA=,cosB=,则△ABC的形状是( )
A.直角三角形 B.钝角三角形 C.锐角三角形 D.锐角三角形或钝角三角形
9.下表是小丽填写的实践活动报告的部分内容:
题目 测量树顶端到地面的高度
测量目标示意图
相关数据 AB=10m,α=45°,β=56°
设树顶端到地面的高度DC为xm,根据以上条件,可以列出求树高的方程为( )
A.x=(x﹣10)cos56° B.x=(x﹣10)tan56°
C.x﹣10=xtan56° D.x=(x+10)sin56°
10.如图,一科珍贵的乌稔树被台风“山竹”吹歪了,处于对它的保护,需要测量它的高度.现采取以下措施:在地面选取一点C,测得∠BCA=45°,AC=20米,
∠BAC=60°,则这棵乌稔树的高AB约为( )(参考数据:1.4,≈1.7)
A.7米 B.14米 C.20米 D.40米
二.填空题(共8小题,每小题3分,共24分)
11.在△ABC中,∠C=90°,如果sinA>cosA,那么∠A的度数范围是 .
12.△ABC中,∠C=90°,tanA=,则sinA+cosA= .
13.在Rt△ABC中,∠C=90°,a,b分别是∠A、∠B的对边,如果sinA:sinB=2:3,那么a:b等于 .
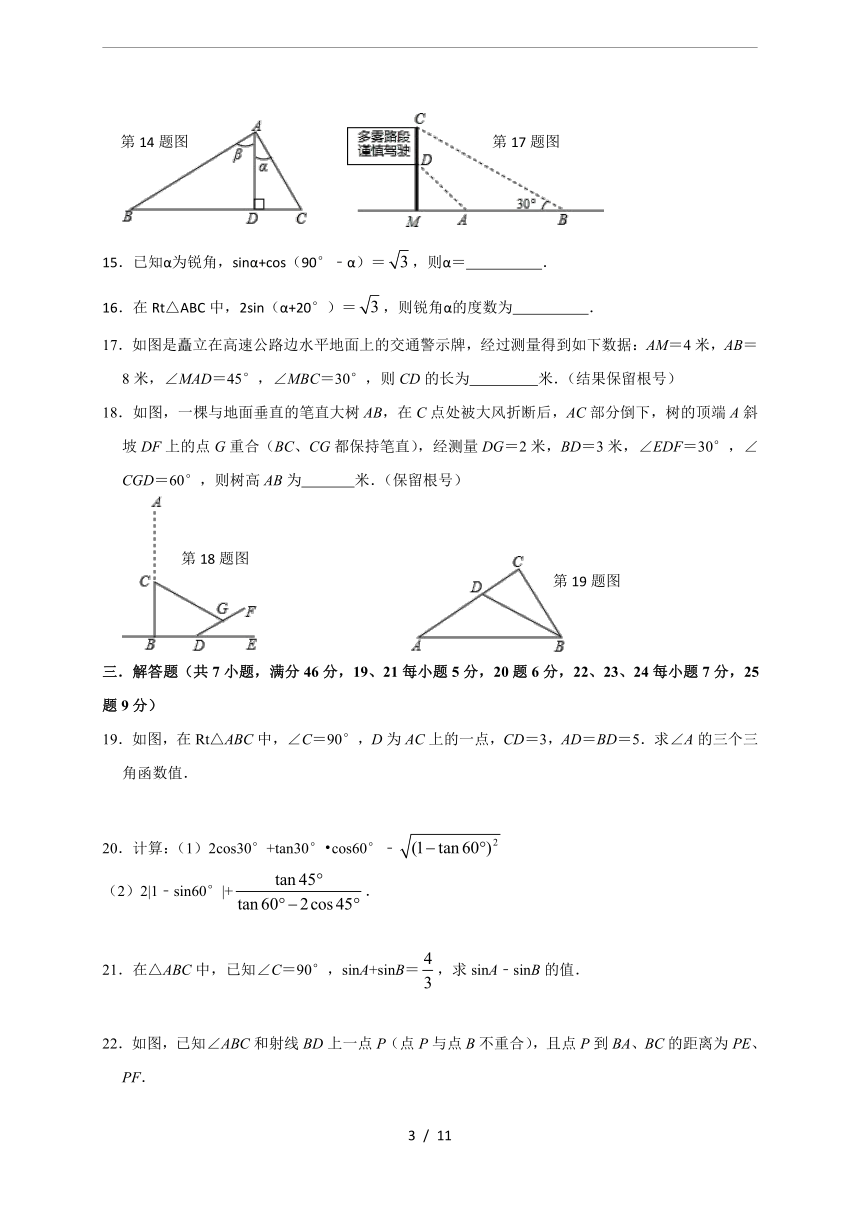
14.如图,在Rt△ABC中,∠A=90°,AD⊥BC,垂足为D.给出下列四个结论:
①sinα=sinB;②sinβ=sinC;③sinB=cosC;④sinα=cosβ.其中正确的结论有 .
15.已知α为锐角,sinα+cos(90°﹣α)=,则α= .
16.在Rt△ABC中,2sin(α+20°)=,则锐角α的度数为 .
17.如图是矗立在高速公路边水平地面上的交通警示牌,经过测量得到如下数据:AM=4米,AB=8米,∠MAD=45°,∠MBC=30°,则CD的长为 米.(结果保留根号)
18.如图,一棵与地面垂直的笔直大树AB,在C点处被大风折断后,AC部分倒下,树的顶端A斜坡DF上的点G重合(BC、CG都保持笔直),经测量DG=2米,BD=3米,∠EDF=30°,∠CGD=60°,则树高AB为 米.(保留根号)
三.解答题(共7小题,满分46分,19、21每小题5分,20题6分,22、23、24每小题7分,25题9分)
19.如图,在Rt△ABC中,∠C=90°,D为AC上的一点,CD=3,AD=BD=5.求∠A的三个三角函数值.
20.计算:(1)2cos30°+tan30°?cos60°﹣
(2)2|1﹣sin60°|+.
21.在△ABC中,已知∠C=90°,sinA+sinB=,求sinA﹣sinB的值.
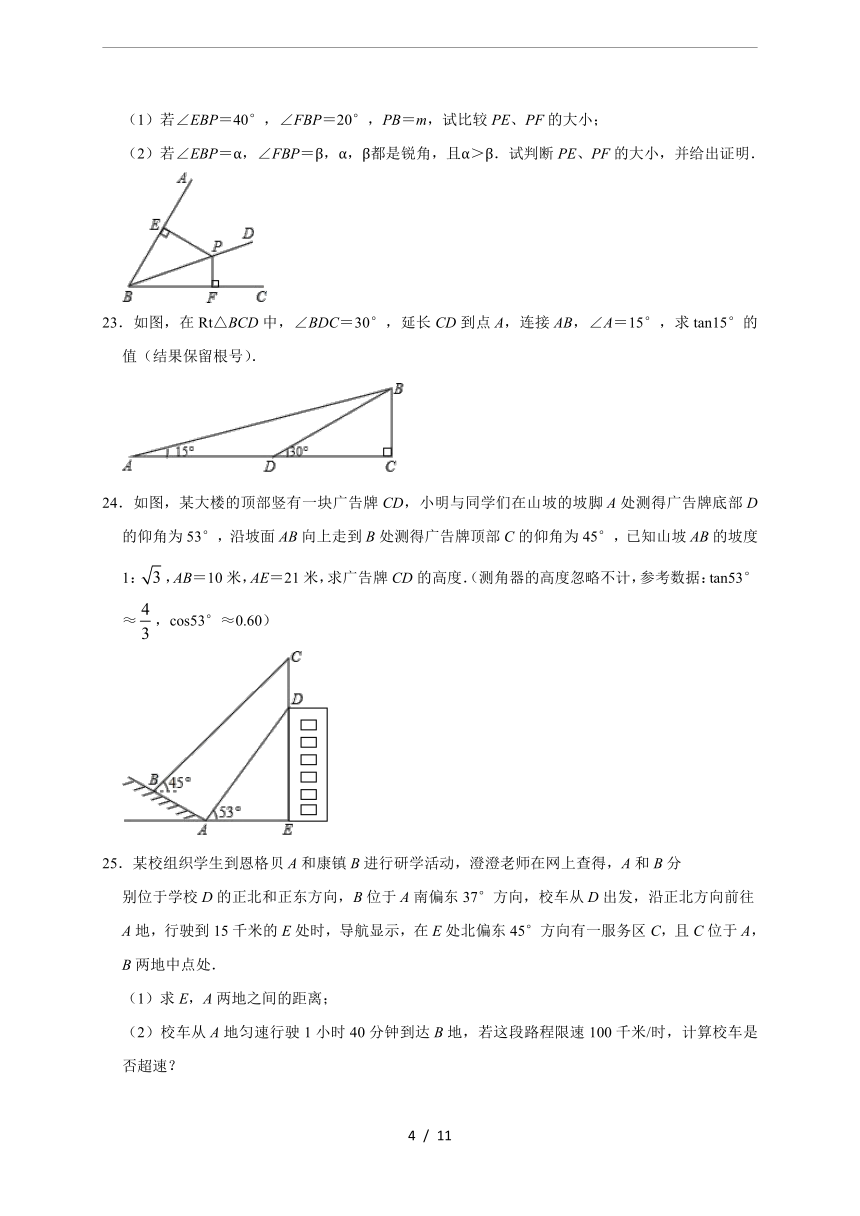
22.如图,已知∠ABC和射线BD上一点P(点P与点B不重合),且点P到BA、BC的距离为PE、PF.
(1)若∠EBP=40°,∠FBP=20°,PB=m,试比较PE、PF的大小;
(2)若∠EBP=α,∠FBP=β,α,β都是锐角,且α>β.试判断PE、PF的大小,并给出证明.
23.如图,在Rt△BCD中,∠BDC=30°,延长CD到点A,连接AB,∠A=15°,求tan15°的值(结果保留根号).
24.如图,某大楼的顶部竖有一块广告牌CD,小明与同学们在山坡的坡脚A处测得广告牌底部D的仰角为53°,沿坡面AB向上走到B处测得广告牌顶部C的仰角为45°,已知山坡AB的坡度1:,AB=10米,AE=21米,求广告牌CD的高度.(测角器的高度忽略不计,参考数据:tan53°≈,cos53°≈0.60)
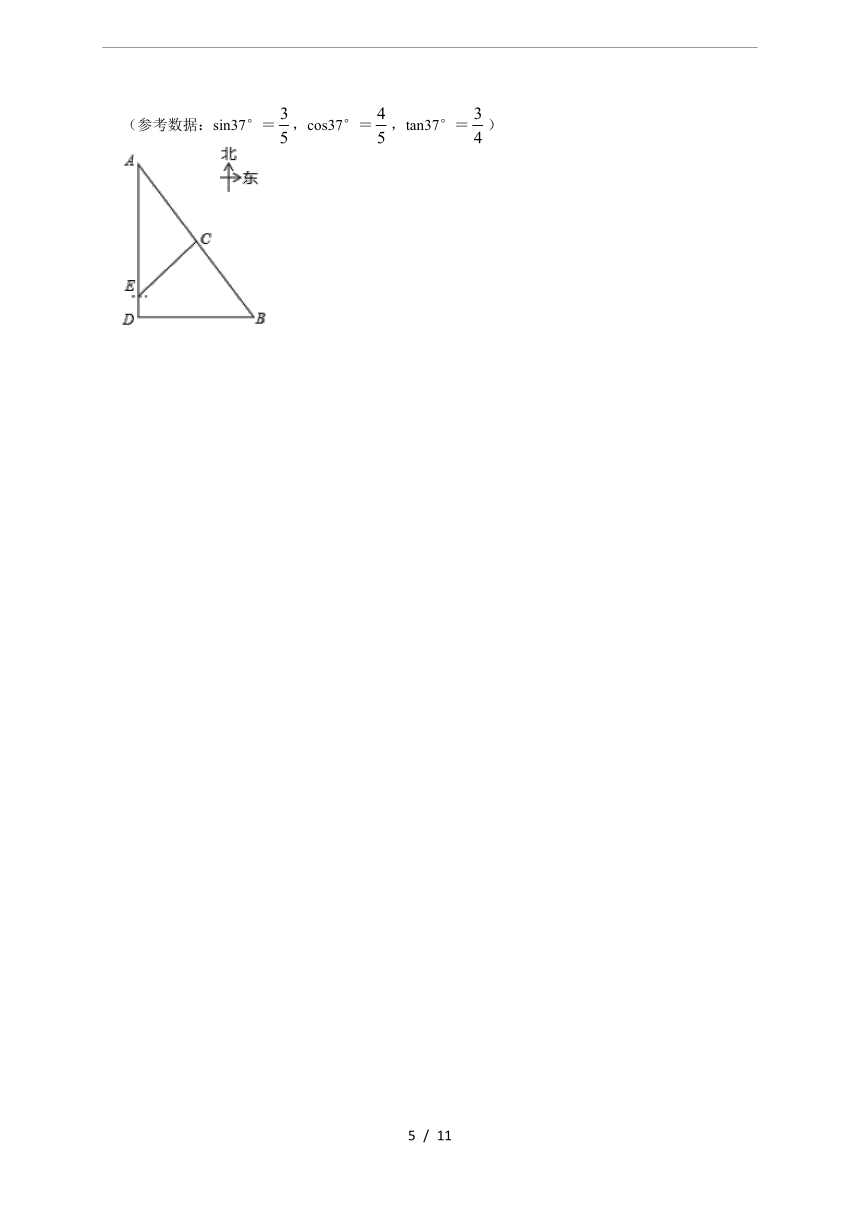
25.某校组织学生到恩格贝A和康镇B进行研学活动,澄澄老师在网上查得,A和B分
别位于学校D的正北和正东方向,B位于A南偏东37°方向,校车从D出发,沿正北方向前往A地,行驶到15千米的E处时,导航显示,在E处北偏东45°方向有一服务区C,且C位于A,B两地中点处.
(1)求E,A两地之间的距离;
(2)校车从A地匀速行驶1小时40分钟到达B地,若这段路程限速100千米/时,计算校车是否超速?
(参考数据:sin37°=,cos37°=,tan37°=)
参考简答
一.选择题(共10小题)
1. B. 2. D. 3. A. 4. A. 5. D. 6. A. 7. A. 8. C.
9. B. 10. B.
二.填空题(共8小题)
11. 45°<∠A<90° . 12. . 13. 2:3 . 14. ①②③④ .
15. 60° . 16. 40° . 17. 4﹣4 .(结果保留根号)
18. 米.(保留根号)
三.解答题(共7小题)
19.如图,在Rt△ABC中,∠C=90°,D为AC上的一点,CD=3,AD=BD=5.求∠A的三个三角函数值.
【解】:在Rt△BCD中,∵CD=3、BD=5,
∴BC===4,
又AC=AD+CD=8,
∴AB===4,
则sinA===,
cosA===,
tanA===.
20.计算:(1)2cos30°+tan30°?cos60°﹣
(2)2|1﹣sin60°|+.
【解】:(1)原式=2×+×﹣+1
=+1.
(2)原式=2(1﹣)+
=2﹣+
=2﹣++
=2+.
21.在△ABC中,已知∠C=90°,sinA+sinB=,求sinA﹣sinB的值.
【解】:∵sinA+sinB=,
∴(sinA+sinB)2=,
∴sin2A+sin2B+2sinA?sinB=,
∵sinB=cosA,
∴sin2A+cos2A+2sinA?sinB=,
∴2sinA?sinB=,
∴(sinA﹣sinB)2=1﹣=,
∴sinA﹣sinB=±.
22.如图,已知∠ABC和射线BD上一点P(点P与点B不重合),且点P到BA、BC的距离为PE、PF.
(1)若∠EBP=40°,∠FBP=20°,PB=m,试比较PE、PF的大小;
(2)若∠EBP=α,∠FBP=β,α,β都是锐角,且α>β.试判断PE、PF的大小,并给出证明.
【解】:(1)在Rt△BPE中,sin∠EBP==sin40°
在Rt△BPF中,sin∠FBP==sin20°
又sin40°>sin20°
∴PE>PF;
(2)根据(1)得
sin∠EBP==sinα,sin∠FBP==sinβ
又∵α>β
∴sinα>sinβ
∴PE>PF.
23.如图,在Rt△BCD中,∠BDC=30°,延长CD到点A,连接AB,∠A=15°,求tan15°的值(结果保留根号).
【解】:∵∠A=15°,∠BDC=30°,
∴∠ABD=15°,
∴AD=BD,
设BC=x,在Rt△BDC中,
∵∠BDC=30°,
∴BD=2x,
∴DC==x,
∴AD=BD=2x,AC=AD+DC=2x+x=(2+)x,
在Rt△ABC中,tan15°===2﹣.
24.如图,某大楼的顶部竖有一块广告牌CD,小明与同学们在山坡的坡脚A处测得广告牌底部D的仰角为53°,沿坡面AB向上走到B处测得广告牌顶部C的仰角为45°,已知山坡AB的坡度1:,AB=10米,AE=21米,求广告牌CD的高度.(测角器的高度忽略不计,参考数据:tan53°≈,cos53°≈0.60)
【解】:过B作BG⊥DE于G,BH⊥AE,
Rt△ABF中,i=tan∠BAH==,
∴∠BAH=30°,
∴BH=AB=5米;
∴AH=5米,
∴BG=AH+AE=(5+21)米,
Rt△BGC中,∠CBG=45°,
∴CG=BG=(5+21)米.
Rt△ADE中,∠DAE=53°,AE=21米,
∴DE=AE=28米.
∴CD=CG+GE﹣DE=26+5﹣28=(5﹣2)m.
答:宣传牌CD高为(5﹣2)米.
25.某校组织学生到恩格贝A和康镇B进行研学活动,澄澄老师在网上查得,A和B分
别位于学校D的正北和正东方向,B位于A南偏东37°方向,校车从D出发,沿正北方向前往A地,行驶到15千米的E处时,导航显示,在E处北偏东45°方向有一服务区C,且C位于A,B两地中点处.
(1)求E,A两地之间的距离;
(2)校车从A地匀速行驶1小时40分钟到达B地,若这段路程限速100千米/时,计算校车是否超速?
(参考数据:sin37°=,cos37°=,tan37°=)
【解】:(1)如图,作CH⊥AD于H.
由题意∠HEC=45°,可得CH=EH,设CH=HE=x千米,
∵点C是AB的中点,CH∥BD,
∴AH=HD=(x+15)千米,
在Rt△ACH中,tan37°=,
∴=,
∴x=45,
∴CH=45(千米),AH=60(千米),AD=120(千米),
∴EA=AD﹣DE=120﹣15=105(千米).
(2)在Rt△ACH中,AC==75(千米),
∴AB=2AC=150(千米),
∵150÷=90千米/小时,
∵90<100,
∴校车没有超速.
第2题图
第1题图
第17题图
第14题图
第19题图
第18题图
PAGE / NUMPAGES
同课章节目录
- 第1章 反比例函数
- 1.1 反比例函数
- 1.2 反比例函数的图像与性质
- 1.3 反比例函数的应用
- 第2章 一元二次方程
- 2.1 一元二次方程
- 2.2 一元二次方程的解法
- 2.3 一元二次方程根的判别式
- 2.4 一元二次方程根与系数的关系
- 2.5 一元二次方程的应用
- 第3章 图形的相似
- 3.1 比例线段
- 3.2 平行线分线段成比例
- 3.3 相似图形
- 3.4 相似三角形的判定与性质
- 3.5 相似三角形的应用
- 3.6 位似
- 第4章 锐角三角函数
- 4.1 正弦和余弦
- 4.2 正切
- 4.3 解直角三角形
- 4.4 解直接三角形的应用
- 第5章 用样本推断总体
- 5.1 总体平均数与方差的估计
- 5.2 统计的简单应用
