2020年北师大版数学九年级下册第3章《圆》单元检测题(含答案)
文档属性
| 名称 | 2020年北师大版数学九年级下册第3章《圆》单元检测题(含答案) |  | |
| 格式 | zip | ||
| 文件大小 | 243.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-02-13 18:19:48 | ||
图片预览


文档简介
北师大版九年级数学下册第3章《圆》单元检测题
(满分:120分 时间:120分钟)
班级 姓名 得分
一、选择题(本大题共12小题,每小题3分,共36分)
1.下列四个命题:①直径是弦;②经过三个点一定可以作圆;③三角形的外心到三角形各顶点的距离都相等;④半径相等的两个半圆是等弧.其中正确的有( )
A.4个 B.3个 C.2个 D.1个
2.如图24?1,已知△ABC是等边三角形,则∠BDC=( )
A.30° B.60° C.90° D.120°
图24?1 图24?2
3.⊙O的半径为8,圆心O到直线l的距离为4,则直线l与⊙O的位置关系是( )
A.相切 B.相交 C.相离 D.不能确定
4.已知:如图24?2,四边形ABCD是⊙O的内接正方形,点P是劣弧上不同于点C的任意一点,则∠BPC的度数是( )
A.45° B.60° C.75° D.90°
5.如图24?3,在平面直角坐标系中,⊙A经过原点O,并且分别与x轴、y轴交于B,C两点,已知B(8,0),C(0,6),则⊙A的半径为( )
A.3 B.4 C.5 D.8
图24?3 图24?4
6.如图24?4,EB为半圆O的直径,点A在EB的延长线上,AD切半圆O于点D,BC⊥AD于点C,AB=2,半圆O的半径为2,则BC的长为( )
A.2 B.1 C.1.5 D.0.5
7.圆内接四边形ABCD,∠A,∠B,∠C的度数之比为3∶4∶6,则∠D的度数为( )
A.60° B.80° C.100° D.120°
8.一个圆锥的冰淇淋纸筒,其底面直径为6 cm,母线长为5 cm,围成这样的冰淇淋纸筒所需纸片的面积为( )
A.15π cm2 B.30π cm2 C.18π cm2 D.12π cm2
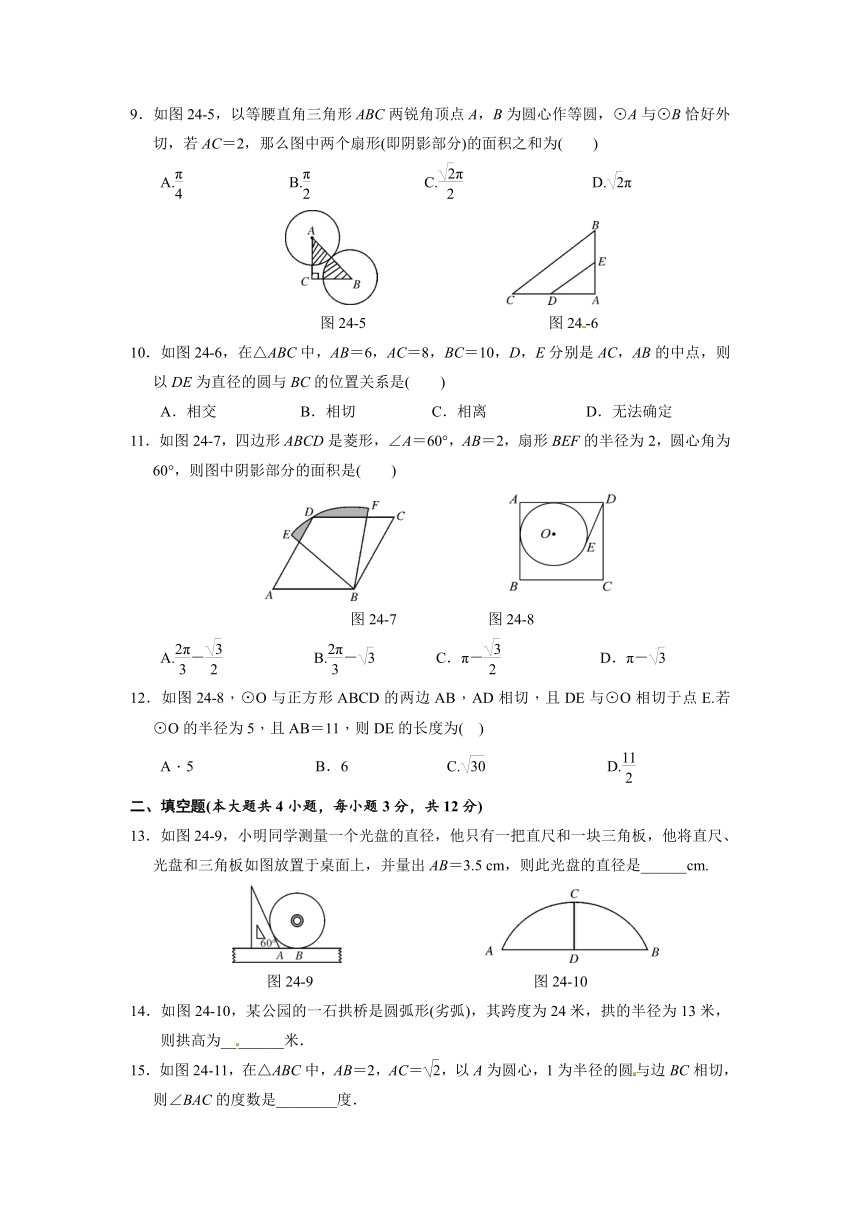
9.如图24?5,以等腰直角三角形ABC两锐角顶点A,B为圆心作等圆,⊙A与⊙B恰好外切,若AC=2,那么图中两个扇形(即阴影部分)的面积之和为( )
A. B. C. D.π
图24?5 图24?6
10.如图24?6,在△ABC中,AB=6,AC=8,BC=10,D,E分别是AC,AB的中点,则以DE为直径的圆与BC的位置关系是( )
A.相交 B.相切 C.相离 D.无法确定
11.如图24?7,四边形ABCD是菱形,∠A=60°,AB=2,扇形BEF的半径为2,圆心角为60°,则图中阴影部分的面积是( )
图24?7 图24-8
A.- B.- C.π- D.π-
12.如图24-8,⊙O与正方形ABCD的两边AB,AD相切,且DE与⊙O相切于点E.若⊙O的半径为5,且AB=11,则DE的长度为( )
A.5 B.6 C. D.
二、填空题(本大题共4小题,每小题3分,共12分)
13.如图24?9,小明同学测量一个光盘的直径,他只有一把直尺和一块三角板,他将直尺、光盘和三角板如图放置于桌面上,并量出AB=3.5 cm,则此光盘的直径是______cm.
图24?9 图24?10
14.如图24?10,某公园的一石拱桥是圆弧形(劣弧),其跨度为24米,拱的半径为13米,则拱高为________米.
15.如图24?11,在△ABC中,AB=2,AC=,以A为圆心,1为半径的圆与边BC相切, 则∠BAC的度数是________度.
图24?11 图24?12
16.如图24?12,一个圆心角为90°的扇形,半径OA=2,那么图中阴影部分的面积为(结果保留π)__________.
三、解答题(6+6+6+6+6+10+10+10+12=72分)
17.如图24?13,⊙O的半径OB=5 cm,AB是⊙O的弦,点C是AB延长线上一点,且∠OCA=30°,OC=8 cm,求AB的长.
图24?13
18.如图24?14,AB是⊙O的直径,=,∠COD=60°.
(1)△AOC是等边三角形吗?请说明理由;
(2)求证:OC∥BD.
图24?14
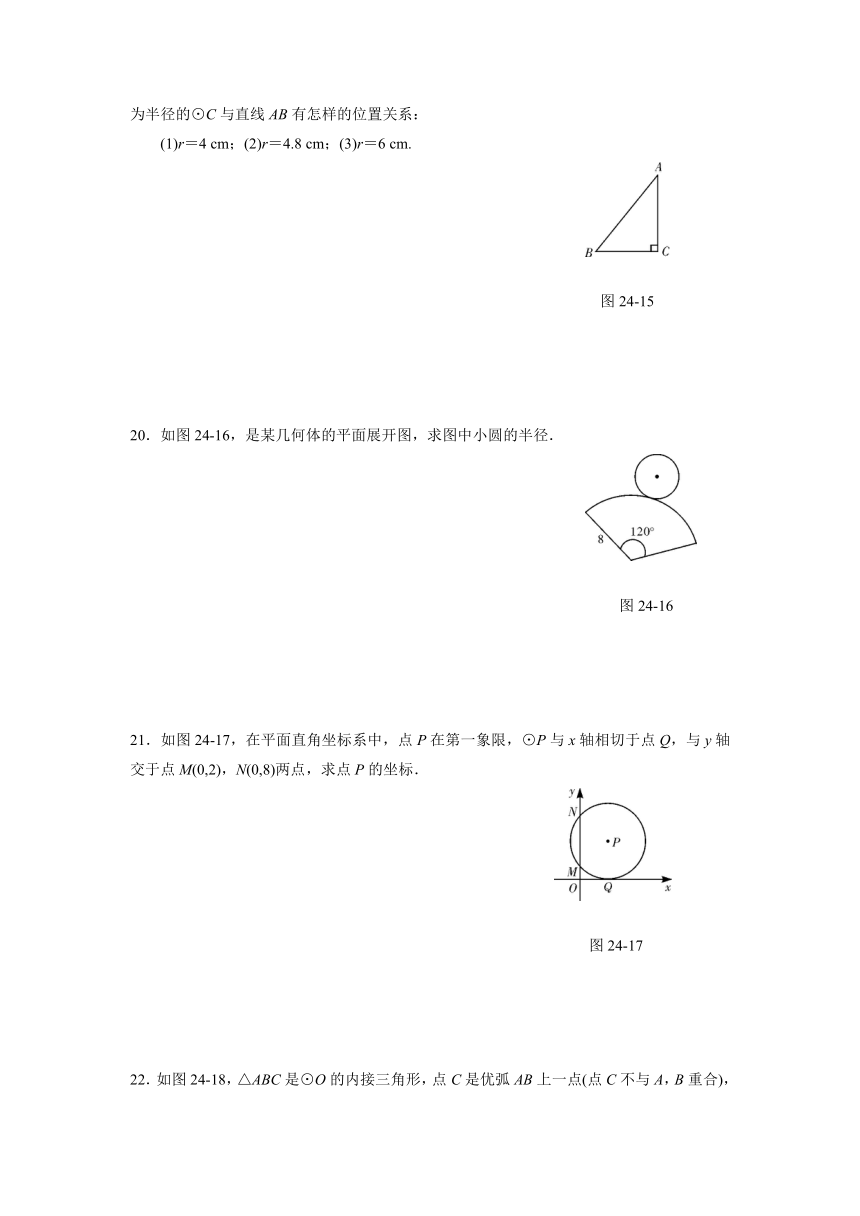
19.如图24?15,在Rt△ABC中,AB=10 cm,BC=6 cm,AC=8 cm,问以点C为圆心,r为半径的⊙C与直线AB有怎样的位置关系:
(1)r=4 cm;(2)r=4.8 cm;(3)r=6 cm.
图24?15
20.如图24?16,是某几何体的平面展开图,求图中小圆的半径.
图24?16
21.如图24?17,在平面直角坐标系中,点P在第一象限,⊙P与x轴相切于点Q,与y轴交于点M(0,2),N(0,8)两点,求点P的坐标.
图24?17
22.如图24?18,△ABC是⊙O的内接三角形,点C是优弧AB上一点(点C不与A,B重合),设∠OAB=α,∠C=β.
(1)当α=35°时,求β的度数;
(2)猜想α与β之间的关系,并给予证明.
图24?18
23.已知:如图24?19,AB是⊙O的直径,AC是弦,直线EF是过点C的⊙O的切线,AD⊥EF于点D.
(1)求证:∠BAC=∠CAD;
(2)若∠B=30°,AB=12,求的长.
图24?19
24.如图24?20,已知AB为⊙O的直径,BD为⊙O的切线,过点B的弦BC⊥OD交⊙O于点C,垂足为点M.
(1)求证:CD是⊙O的切线;
(2)当BC=BD,且BD=6 cm时,求图中阴影部分的面积(结果不取近似值).
图24?20
25.(12分)如图24-21,⊙O的弦AD∥BC,过点D的切线交BC的延长线于点E,AC∥DE交BD于点H,DO及延长线分别交AC,BC于点G,F.
(1)求证:DF垂直平分AC;
(2)求证:FC=CE;
(3)若弦AD=5 cm,AC=8 cm,求⊙O的半径.
图24-21
参考答案
1.B 2.B 3.B 4.A 5.C 6.B 7.C 8.A 9.B 10.A 11.B 12.B
13.7 14.8 15.105 16.π-2
17.解:过点O作OD⊥AB于点D,则AD=BD.
在Rt△DOC中,∠OCA=30°,OC=8 cm,
∴OD=OC=4(cm).
在Rt△OBD中,BD===3(cm),
∴AB=2BD=6(cm).
18.(1)解:△AOC是等边三角形.
证明如下:
∵=,∴∠AOC=∠COD=60°.
∵OA=OC(⊙O的半径),∴△AOC是等边三角形.
(2)证明:∵ =,∴OC⊥AD.
又∵AB是⊙O的直径,
∴∠ADB=90°,即BD⊥AD.
∴OC∥BD.
19.解:过点C作CD⊥AB于点D.
则CD==4.8(cm).
(1)当r=4 cm时,CD>r,∴⊙C与直线AB相离.
(2)当r=4.8 cm时,CD=r,∴⊙C与直线AB相切.
(3)当r=6 cm时,CD<r,∴⊙C与直线AB相交.
20.解:这个几何体是圆锥,假设图中小圆的半径为r,
∵扇形弧长等于小圆的周长,
∴l=·π·8=2·π·r.
∴r=.
21.解:作PA⊥MN,交MN于点A,则MA=NA.
又M(0,2),N(0,8),∴MN=6.∴MA=NA=3.
∴OA=5.
连接PQ,则PQ=OA=5.∴MP=5.
∴AP==4.∴点P坐标为(4,5).
22.解:(1)连接OB,则OA=OB.∴∠OBA=∠OAB=35°.
∴∠AOB=180°-∠OAB-∠OBA=110°.
∴β=∠C=∠AOB=55°.
(2)α与β的关系是α+β=90°.证明如下:
连接OB,则OA=OB.
∴∠OBA=∠OAB=α.∴∠AOB=180°-2α.
∴β=∠C=∠AOB=(180°-2α)=90°-α.
∴α+β=90°.
23.(1)证明:如图D93,连接OC,
图D93
∵EF是过点C的⊙O的切线,
∴OC⊥EF.
又∵AD⊥EF,
∴OC∥AD.∴∠OCA=∠CAD.
又∵OA=OC,
∴∠OCA=∠BAC.∴∠BAC=∠CAD.
(2)解:∵OB=OC,∴∠B=∠OCB=30°.
又∵∠AOC是△BOC的外角,
∴∠AOC=∠B+∠OCB=60°.
∵AB=12,∴半径OA=AB=6.
∴的长为l==2π.
24.(1)证明:连接OC.
∵OD⊥BC,O为圆心,
∴OD平分BC.∴DB=DC.
∴△OBD≌△OCD(SSS).
∴∠OCD=∠OBD.
又∵BD为⊙O的切线,∴∠OCD=∠OBD=90°.
∴CD是⊙O的切线.
(2)解:∵DB,DC为切线,B,C为切点,
∴DB=DC.
又∵DB=BC=6,∴△BCD为等边三角形.
∴∠BOC=360°-90°-90°-60°=120°,
∠OBM=90°-60°=30°,BM=3.
∴OM=,OB=2 .
∴S阴影部分=S扇形OBC-S△OBC
=-×6×=4π-3 (cm2).
25.解:(1)∵DF⊥DE,AC∥DE,∴DF⊥AC,∴DF垂直平分AC
(2)由(1)知AG=GC,又∵AD∥BC,∴∠DAG=∠FCG,
又∠AGD=∠CGF,∴△AGD≌△CGF,∴AD=FC.∵AD∥BC且AC∥DE,
∴四边形ACED是平行四边形,∴AD=CE,∴FC=CE
(3)连接AO,∵AG=GC,AC=8 cm,∴AG=4 cm,GD==3 (cm).
设圆半径为r,则AO=r,OG=r-3,
由勾股定理有AO2=OG2+AG2,∴r2=(r-3)2+42,∴r= cm
(满分:120分 时间:120分钟)
班级 姓名 得分
一、选择题(本大题共12小题,每小题3分,共36分)
1.下列四个命题:①直径是弦;②经过三个点一定可以作圆;③三角形的外心到三角形各顶点的距离都相等;④半径相等的两个半圆是等弧.其中正确的有( )
A.4个 B.3个 C.2个 D.1个
2.如图24?1,已知△ABC是等边三角形,则∠BDC=( )
A.30° B.60° C.90° D.120°
图24?1 图24?2
3.⊙O的半径为8,圆心O到直线l的距离为4,则直线l与⊙O的位置关系是( )
A.相切 B.相交 C.相离 D.不能确定
4.已知:如图24?2,四边形ABCD是⊙O的内接正方形,点P是劣弧上不同于点C的任意一点,则∠BPC的度数是( )
A.45° B.60° C.75° D.90°
5.如图24?3,在平面直角坐标系中,⊙A经过原点O,并且分别与x轴、y轴交于B,C两点,已知B(8,0),C(0,6),则⊙A的半径为( )
A.3 B.4 C.5 D.8
图24?3 图24?4
6.如图24?4,EB为半圆O的直径,点A在EB的延长线上,AD切半圆O于点D,BC⊥AD于点C,AB=2,半圆O的半径为2,则BC的长为( )
A.2 B.1 C.1.5 D.0.5
7.圆内接四边形ABCD,∠A,∠B,∠C的度数之比为3∶4∶6,则∠D的度数为( )
A.60° B.80° C.100° D.120°
8.一个圆锥的冰淇淋纸筒,其底面直径为6 cm,母线长为5 cm,围成这样的冰淇淋纸筒所需纸片的面积为( )
A.15π cm2 B.30π cm2 C.18π cm2 D.12π cm2
9.如图24?5,以等腰直角三角形ABC两锐角顶点A,B为圆心作等圆,⊙A与⊙B恰好外切,若AC=2,那么图中两个扇形(即阴影部分)的面积之和为( )
A. B. C. D.π
图24?5 图24?6
10.如图24?6,在△ABC中,AB=6,AC=8,BC=10,D,E分别是AC,AB的中点,则以DE为直径的圆与BC的位置关系是( )
A.相交 B.相切 C.相离 D.无法确定
11.如图24?7,四边形ABCD是菱形,∠A=60°,AB=2,扇形BEF的半径为2,圆心角为60°,则图中阴影部分的面积是( )
图24?7 图24-8
A.- B.- C.π- D.π-
12.如图24-8,⊙O与正方形ABCD的两边AB,AD相切,且DE与⊙O相切于点E.若⊙O的半径为5,且AB=11,则DE的长度为( )
A.5 B.6 C. D.
二、填空题(本大题共4小题,每小题3分,共12分)
13.如图24?9,小明同学测量一个光盘的直径,他只有一把直尺和一块三角板,他将直尺、光盘和三角板如图放置于桌面上,并量出AB=3.5 cm,则此光盘的直径是______cm.
图24?9 图24?10
14.如图24?10,某公园的一石拱桥是圆弧形(劣弧),其跨度为24米,拱的半径为13米,则拱高为________米.
15.如图24?11,在△ABC中,AB=2,AC=,以A为圆心,1为半径的圆与边BC相切, 则∠BAC的度数是________度.
图24?11 图24?12
16.如图24?12,一个圆心角为90°的扇形,半径OA=2,那么图中阴影部分的面积为(结果保留π)__________.
三、解答题(6+6+6+6+6+10+10+10+12=72分)
17.如图24?13,⊙O的半径OB=5 cm,AB是⊙O的弦,点C是AB延长线上一点,且∠OCA=30°,OC=8 cm,求AB的长.
图24?13
18.如图24?14,AB是⊙O的直径,=,∠COD=60°.
(1)△AOC是等边三角形吗?请说明理由;
(2)求证:OC∥BD.
图24?14
19.如图24?15,在Rt△ABC中,AB=10 cm,BC=6 cm,AC=8 cm,问以点C为圆心,r为半径的⊙C与直线AB有怎样的位置关系:
(1)r=4 cm;(2)r=4.8 cm;(3)r=6 cm.
图24?15
20.如图24?16,是某几何体的平面展开图,求图中小圆的半径.
图24?16
21.如图24?17,在平面直角坐标系中,点P在第一象限,⊙P与x轴相切于点Q,与y轴交于点M(0,2),N(0,8)两点,求点P的坐标.
图24?17
22.如图24?18,△ABC是⊙O的内接三角形,点C是优弧AB上一点(点C不与A,B重合),设∠OAB=α,∠C=β.
(1)当α=35°时,求β的度数;
(2)猜想α与β之间的关系,并给予证明.
图24?18
23.已知:如图24?19,AB是⊙O的直径,AC是弦,直线EF是过点C的⊙O的切线,AD⊥EF于点D.
(1)求证:∠BAC=∠CAD;
(2)若∠B=30°,AB=12,求的长.
图24?19
24.如图24?20,已知AB为⊙O的直径,BD为⊙O的切线,过点B的弦BC⊥OD交⊙O于点C,垂足为点M.
(1)求证:CD是⊙O的切线;
(2)当BC=BD,且BD=6 cm时,求图中阴影部分的面积(结果不取近似值).
图24?20
25.(12分)如图24-21,⊙O的弦AD∥BC,过点D的切线交BC的延长线于点E,AC∥DE交BD于点H,DO及延长线分别交AC,BC于点G,F.
(1)求证:DF垂直平分AC;
(2)求证:FC=CE;
(3)若弦AD=5 cm,AC=8 cm,求⊙O的半径.
图24-21
参考答案
1.B 2.B 3.B 4.A 5.C 6.B 7.C 8.A 9.B 10.A 11.B 12.B
13.7 14.8 15.105 16.π-2
17.解:过点O作OD⊥AB于点D,则AD=BD.
在Rt△DOC中,∠OCA=30°,OC=8 cm,
∴OD=OC=4(cm).
在Rt△OBD中,BD===3(cm),
∴AB=2BD=6(cm).
18.(1)解:△AOC是等边三角形.
证明如下:
∵=,∴∠AOC=∠COD=60°.
∵OA=OC(⊙O的半径),∴△AOC是等边三角形.
(2)证明:∵ =,∴OC⊥AD.
又∵AB是⊙O的直径,
∴∠ADB=90°,即BD⊥AD.
∴OC∥BD.
19.解:过点C作CD⊥AB于点D.
则CD==4.8(cm).
(1)当r=4 cm时,CD>r,∴⊙C与直线AB相离.
(2)当r=4.8 cm时,CD=r,∴⊙C与直线AB相切.
(3)当r=6 cm时,CD<r,∴⊙C与直线AB相交.
20.解:这个几何体是圆锥,假设图中小圆的半径为r,
∵扇形弧长等于小圆的周长,
∴l=·π·8=2·π·r.
∴r=.
21.解:作PA⊥MN,交MN于点A,则MA=NA.
又M(0,2),N(0,8),∴MN=6.∴MA=NA=3.
∴OA=5.
连接PQ,则PQ=OA=5.∴MP=5.
∴AP==4.∴点P坐标为(4,5).
22.解:(1)连接OB,则OA=OB.∴∠OBA=∠OAB=35°.
∴∠AOB=180°-∠OAB-∠OBA=110°.
∴β=∠C=∠AOB=55°.
(2)α与β的关系是α+β=90°.证明如下:
连接OB,则OA=OB.
∴∠OBA=∠OAB=α.∴∠AOB=180°-2α.
∴β=∠C=∠AOB=(180°-2α)=90°-α.
∴α+β=90°.
23.(1)证明:如图D93,连接OC,
图D93
∵EF是过点C的⊙O的切线,
∴OC⊥EF.
又∵AD⊥EF,
∴OC∥AD.∴∠OCA=∠CAD.
又∵OA=OC,
∴∠OCA=∠BAC.∴∠BAC=∠CAD.
(2)解:∵OB=OC,∴∠B=∠OCB=30°.
又∵∠AOC是△BOC的外角,
∴∠AOC=∠B+∠OCB=60°.
∵AB=12,∴半径OA=AB=6.
∴的长为l==2π.
24.(1)证明:连接OC.
∵OD⊥BC,O为圆心,
∴OD平分BC.∴DB=DC.
∴△OBD≌△OCD(SSS).
∴∠OCD=∠OBD.
又∵BD为⊙O的切线,∴∠OCD=∠OBD=90°.
∴CD是⊙O的切线.
(2)解:∵DB,DC为切线,B,C为切点,
∴DB=DC.
又∵DB=BC=6,∴△BCD为等边三角形.
∴∠BOC=360°-90°-90°-60°=120°,
∠OBM=90°-60°=30°,BM=3.
∴OM=,OB=2 .
∴S阴影部分=S扇形OBC-S△OBC
=-×6×=4π-3 (cm2).
25.解:(1)∵DF⊥DE,AC∥DE,∴DF⊥AC,∴DF垂直平分AC
(2)由(1)知AG=GC,又∵AD∥BC,∴∠DAG=∠FCG,
又∠AGD=∠CGF,∴△AGD≌△CGF,∴AD=FC.∵AD∥BC且AC∥DE,
∴四边形ACED是平行四边形,∴AD=CE,∴FC=CE
(3)连接AO,∵AG=GC,AC=8 cm,∴AG=4 cm,GD==3 (cm).
设圆半径为r,则AO=r,OG=r-3,
由勾股定理有AO2=OG2+AG2,∴r2=(r-3)2+42,∴r= cm
