苏科版八年级数学下册 7.3频数与频率课件(共33张PPT)
文档属性
| 名称 | 苏科版八年级数学下册 7.3频数与频率课件(共33张PPT) |  | |
| 格式 | zip | ||
| 文件大小 | 3.0MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-02-13 18:20:36 | ||
图片预览











文档简介
(共33张PPT)
7.3 频数与频率
1.我们曾经学过哪些收集数据的方法?
答:我们可以通过调查问卷、查阅资料等方式收集数据.
2.对于收集到的数据,我们可以如何来描述它们呢?
答:可以绘制统计图和统计表.
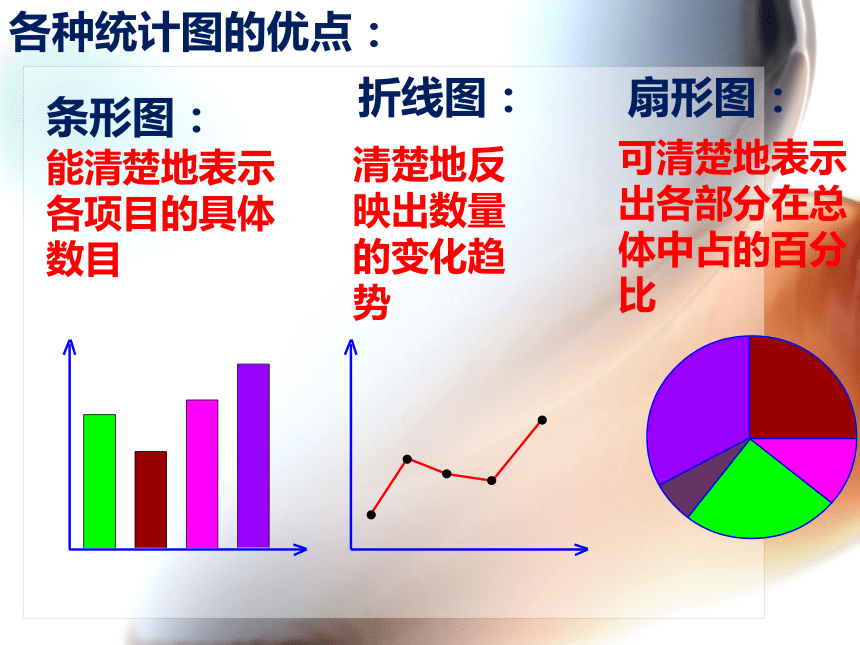
各种统计图的优点:
条形图:
扇形图:
折线图:
能清楚地表示各项目的具体数目
可清楚地表示出各部分在总体中占的百分比
清楚地反映出数量的变化趋势
4.这些方法是否能够处理所有关于数据的工作呢?
你喜欢看篮球比赛吗?你最喜欢的中国篮球明星是谁?
姚明
易建联
孙悦
王治郅
小明调查了八(1)班50位同学最喜欢的篮球明星,结果如下 :
A A B C D A B A A C
B A A C B C A A B C
A A B A C D A A C D
B A C D A A A C D A
C B A A C C D A A C
其中 A代表姚明, B代表孙悦,
C代表易建联, D代表王治郅
答:因为数据太多,很难较快的说出.
(1) 根据上面的结果,你能很快说出该班同学最喜欢的篮球明星吗?
(2) 你认为小明的数据表示方式好不好?你能设计出一个比较好的表示方式吗?
小丽根据小明的结果制成了下面的图表,你能从中迅速判断出该班同学最喜欢的篮球明星吗 ?
篮球
明星 学生数
A 正正正正 23
B 正 8
C 正正 13
D 正 6
从上表可以看出,A,B,C,D出现的次数有的多,有的少,或者说它们出现的频繁程度不同 。
篮球
明星 学生数
A 正正正正 23
B 正 8
C 正正 13
D 正 6
一般地,一组数据中,每个数据出现的次数称为此数据的频数,而每个数据出现的次数与总次数的比值称为此数据的频率。如,A的频数为23,A的频率为
填表:
0.46
0.16
0.26
0.12
50
1
23
8
13
6
由上表你有何发现?
篮球明星 学生数 频数 频率
A 正正正正
B 正
C 正正
D 正
合计 50
频率=
频数=
频数、频率和总次数之间的关系:
总次数=
总次数 × 频率
(1)各对象的频数之和等于数据总个数;
(2)各对象的频率之和等于1;
前15 次射击得分情况
后15 次射击得分情况
(1) 用表格表示小芳射击训练中前15次和后15次射击得分的频数和频率.
(2) 分别求出前15次和后15次射击得分的平均数(精确到 0.01),比较射击成绩的变化.
次 数 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15
环 数 7 8 7 7 8 9 8 8 9 7 8 7 7 9 9
次 数 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30
环 数 8 8 7 10 8 9 9 8 9 10 10 9 9 8 10
次 数 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15
环 数 7 8 7 7 8 9 8 8 9 7 8 7 7 9 9
前15 次射击得分情况
0.33
后15 次射击得分情况
从表中可以看出,小芳前15次的射击成绩中,7 环最多,8 环其次,9 环较少,10 环没有;后15 次射击成绩中,7 环最少,8 环和9 环最多,10 环有4次.
环数 7 8 9 10
频数 6 5 4 0
频率 0.40 0.33 0.27 0
环数 7 8 9 10
频数 1 5 5 4
频率 0.07 0.33 0.27
后15 次平均数大,说明经过调整射击方法后,
小芳得高分的次数增加,平均成绩得到了提高.
同理可求得后15次射击成绩的平均数是8.80.
1.一组数据中共有40个数,其中53出现的频率为0.3,则这40个数中,53出现的频数为 。
2.把50个数据分成六组,其中有一组的频数是14,有两组的频数是10,有两组的频率是 0.14,
则另一组的频数是 ,频率是 。
12
2
0.04
3.为了了解某种小麦麦穗的长度,科技人员抽测实验田麦穗的长度,列表如下:
(1)表中未完成部分:
a=__ , b=__ , c=__, d=__,
e=__ , f=__ , g=____.
(2)长度在5.95—6.45cm的麦穗
占总数的百分之几? ______.
(3)众数在_____组,中位数在___组.
1
0.1
5
a
1
e
0.10
c
5
20
d
20
6
b
6
0.3
f
0.30
1
g
1
30%
3,4
4
组数 分组 频数 频率
1 4.45—4.95 0.05
2 4.95—5.45 2
3 5.45—5.95 6 0.30
4 5.95—6.45
5 6.45—6.95 0.25
合计
频数 :
频率:
每个数据出现的次数。
每个数据的次数与总次数的比值。
频率=
频数之和等于总次数,频率之和等于1。
一枚硬币有两面,我们称有国徽的一面为“正面”,
另一面为“反面”;掷一枚硬币,当硬币落下时,可能
出现“正面朝上”,也可能出现“反面朝上”.
每次掷币,两种情形必然出现一种,也只能出现一种. 究竟出现哪种情形,在掷币之前无法预计,只有掷币之后才能知道.
与同桌同学合作,掷10次硬币,并把10次试验结果记录下来:
(1) 计算“正面朝上” 和“反面朝上” 的频数各是多少,它们之间有什么关系?
(2) 计算“正面朝上” 和“反面朝上” 的频率各是多少,它们之间有什么关系?
次数 1 2 3 4 5 6 7 8 9 10
结果(正或反)
假设某同学掷10次硬币的结果如下:
次数 1 2 3 4 5 6 7 8 9 10
结果 反 正 正 正 反 反 反 正 反 反
正
正
正
正
可以发现,“正面朝上” 和“反面朝上” 的频数之和为试验总次数;而这两种情况的频率之和为1.
次数 1 2 3 4 5 6 7 8 9 10
结果 反 反 反 反 反 反
一次掷两枚硬币,用A,B,C分别代表可能发生的三种情形:
A. 两枚硬币都是正面朝上;
B. 两枚硬币都是反面朝上;
C. 一枚硬币正面朝上,另一枚硬币反面朝上.
每次掷币都发生A,B,C三种情形中的一种,并且只发生一种.
A,B,C发生的频数与频率
现在全班同学每人各掷两枚硬币5 次,记录所得结果, 将全班的结果汇总填入下表中,并计算频率.
说一说,出现哪一种情形的频率高?
频数 频率
A
B
C
合计
全班每组同学抛掷一枚硬币40 次,记录出现“正面朝上”的结果,将各组试验结果汇总,完成下表:
累计掷币次数 40 80 120 160 200 240
“正面朝上” 的频数m
“正面朝上” 的频率
根据上表, 在下图中绘制“正面朝上” 的频率变化折线统计图.
例
某校为了了解九年级学生的体能情况,随机抽查了其中的30名学生,测试了1分钟仰卧起坐的次数,并绘制成如下图所示的频数分布直方图,请根据图示计算,仰卧起坐次数在15~20次之间的频率是( ).
A.0.1 B.0.17 C.0.33 D.0.4
A
一般地,一组数据中,每个数据出现的次数称为此数据的频数,而每个数据出现的次数与总次数的比值称为此数据的频率。
频数 :
频率:
每个数据出现的次数。
每个数据的次数与总次数的比值。
频率=
频数之和等于总次数,频率之和等于1。
7.3 频数与频率
1.我们曾经学过哪些收集数据的方法?
答:我们可以通过调查问卷、查阅资料等方式收集数据.
2.对于收集到的数据,我们可以如何来描述它们呢?
答:可以绘制统计图和统计表.
各种统计图的优点:
条形图:
扇形图:
折线图:
能清楚地表示各项目的具体数目
可清楚地表示出各部分在总体中占的百分比
清楚地反映出数量的变化趋势
4.这些方法是否能够处理所有关于数据的工作呢?
你喜欢看篮球比赛吗?你最喜欢的中国篮球明星是谁?
姚明
易建联
孙悦
王治郅
小明调查了八(1)班50位同学最喜欢的篮球明星,结果如下 :
A A B C D A B A A C
B A A C B C A A B C
A A B A C D A A C D
B A C D A A A C D A
C B A A C C D A A C
其中 A代表姚明, B代表孙悦,
C代表易建联, D代表王治郅
答:因为数据太多,很难较快的说出.
(1) 根据上面的结果,你能很快说出该班同学最喜欢的篮球明星吗?
(2) 你认为小明的数据表示方式好不好?你能设计出一个比较好的表示方式吗?
小丽根据小明的结果制成了下面的图表,你能从中迅速判断出该班同学最喜欢的篮球明星吗 ?
篮球
明星 学生数
A 正正正正 23
B 正 8
C 正正 13
D 正 6
从上表可以看出,A,B,C,D出现的次数有的多,有的少,或者说它们出现的频繁程度不同 。
篮球
明星 学生数
A 正正正正 23
B 正 8
C 正正 13
D 正 6
一般地,一组数据中,每个数据出现的次数称为此数据的频数,而每个数据出现的次数与总次数的比值称为此数据的频率。如,A的频数为23,A的频率为
填表:
0.46
0.16
0.26
0.12
50
1
23
8
13
6
由上表你有何发现?
篮球明星 学生数 频数 频率
A 正正正正
B 正
C 正正
D 正
合计 50
频率=
频数=
频数、频率和总次数之间的关系:
总次数=
总次数 × 频率
(1)各对象的频数之和等于数据总个数;
(2)各对象的频率之和等于1;
前15 次射击得分情况
后15 次射击得分情况
(1) 用表格表示小芳射击训练中前15次和后15次射击得分的频数和频率.
(2) 分别求出前15次和后15次射击得分的平均数(精确到 0.01),比较射击成绩的变化.
次 数 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15
环 数 7 8 7 7 8 9 8 8 9 7 8 7 7 9 9
次 数 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30
环 数 8 8 7 10 8 9 9 8 9 10 10 9 9 8 10
次 数 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15
环 数 7 8 7 7 8 9 8 8 9 7 8 7 7 9 9
前15 次射击得分情况
0.33
后15 次射击得分情况
从表中可以看出,小芳前15次的射击成绩中,7 环最多,8 环其次,9 环较少,10 环没有;后15 次射击成绩中,7 环最少,8 环和9 环最多,10 环有4次.
环数 7 8 9 10
频数 6 5 4 0
频率 0.40 0.33 0.27 0
环数 7 8 9 10
频数 1 5 5 4
频率 0.07 0.33 0.27
后15 次平均数大,说明经过调整射击方法后,
小芳得高分的次数增加,平均成绩得到了提高.
同理可求得后15次射击成绩的平均数是8.80.
1.一组数据中共有40个数,其中53出现的频率为0.3,则这40个数中,53出现的频数为 。
2.把50个数据分成六组,其中有一组的频数是14,有两组的频数是10,有两组的频率是 0.14,
则另一组的频数是 ,频率是 。
12
2
0.04
3.为了了解某种小麦麦穗的长度,科技人员抽测实验田麦穗的长度,列表如下:
(1)表中未完成部分:
a=__ , b=__ , c=__, d=__,
e=__ , f=__ , g=____.
(2)长度在5.95—6.45cm的麦穗
占总数的百分之几? ______.
(3)众数在_____组,中位数在___组.
1
0.1
5
a
1
e
0.10
c
5
20
d
20
6
b
6
0.3
f
0.30
1
g
1
30%
3,4
4
组数 分组 频数 频率
1 4.45—4.95 0.05
2 4.95—5.45 2
3 5.45—5.95 6 0.30
4 5.95—6.45
5 6.45—6.95 0.25
合计
频数 :
频率:
每个数据出现的次数。
每个数据的次数与总次数的比值。
频率=
频数之和等于总次数,频率之和等于1。
一枚硬币有两面,我们称有国徽的一面为“正面”,
另一面为“反面”;掷一枚硬币,当硬币落下时,可能
出现“正面朝上”,也可能出现“反面朝上”.
每次掷币,两种情形必然出现一种,也只能出现一种. 究竟出现哪种情形,在掷币之前无法预计,只有掷币之后才能知道.
与同桌同学合作,掷10次硬币,并把10次试验结果记录下来:
(1) 计算“正面朝上” 和“反面朝上” 的频数各是多少,它们之间有什么关系?
(2) 计算“正面朝上” 和“反面朝上” 的频率各是多少,它们之间有什么关系?
次数 1 2 3 4 5 6 7 8 9 10
结果(正或反)
假设某同学掷10次硬币的结果如下:
次数 1 2 3 4 5 6 7 8 9 10
结果 反 正 正 正 反 反 反 正 反 反
正
正
正
正
可以发现,“正面朝上” 和“反面朝上” 的频数之和为试验总次数;而这两种情况的频率之和为1.
次数 1 2 3 4 5 6 7 8 9 10
结果 反 反 反 反 反 反
一次掷两枚硬币,用A,B,C分别代表可能发生的三种情形:
A. 两枚硬币都是正面朝上;
B. 两枚硬币都是反面朝上;
C. 一枚硬币正面朝上,另一枚硬币反面朝上.
每次掷币都发生A,B,C三种情形中的一种,并且只发生一种.
A,B,C发生的频数与频率
现在全班同学每人各掷两枚硬币5 次,记录所得结果, 将全班的结果汇总填入下表中,并计算频率.
说一说,出现哪一种情形的频率高?
频数 频率
A
B
C
合计
全班每组同学抛掷一枚硬币40 次,记录出现“正面朝上”的结果,将各组试验结果汇总,完成下表:
累计掷币次数 40 80 120 160 200 240
“正面朝上” 的频数m
“正面朝上” 的频率
根据上表, 在下图中绘制“正面朝上” 的频率变化折线统计图.
例
某校为了了解九年级学生的体能情况,随机抽查了其中的30名学生,测试了1分钟仰卧起坐的次数,并绘制成如下图所示的频数分布直方图,请根据图示计算,仰卧起坐次数在15~20次之间的频率是( ).
A.0.1 B.0.17 C.0.33 D.0.4
A
一般地,一组数据中,每个数据出现的次数称为此数据的频数,而每个数据出现的次数与总次数的比值称为此数据的频率。
频数 :
频率:
每个数据出现的次数。
每个数据的次数与总次数的比值。
频率=
频数之和等于总次数,频率之和等于1。
同课章节目录
- 第7章 数据的收集、整理、描述
- 7.1 普查与抽样调查
- 7.2 统计图的选用
- 7.3 频数和频率
- 7.4 频数分布表和频数分布直方图
- 第8章 认识概率
- 8.1 确定事件与随机事件
- 8.2 可能性的大小
- 8.3 频率与概率
- 第9章 中心对称图形——平行四边形
- 9.1 图形的旋转
- 9.2 中心对称与中心对称图形
- 9.3 平行四边形
- 9.4 矩形、菱形、正方形
- 9.5 三角形的中位线
- 第10章 分式
- 10.1 分式
- 10.2 分式的基本性质
- 10.3 分式的加减
- 10.4 分式的乘除
- 10.5 分式方程
- 第11章 反比例函数
- 11.1 反比例函数
- 11.2 反比例函数的图象与性质
- 11.3 用反比例函数解决问题
- 第12章 二次根式
- 12.1 二次根式
- 12.2 二次根式的乘除
- 12.3 二次根式的加减
