人教版八年级数学下册 17.2勾股定理的逆定理课件(共24张PPT)
文档属性
| 名称 | 人教版八年级数学下册 17.2勾股定理的逆定理课件(共24张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 1.3MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-02-14 00:00:00 | ||
图片预览


文档简介
(共24张PPT)
如果三角形的三边长a、b、c满足
a2 + b2 = c2
那么这个三角形是直角三角形。
回顾与思考
勾股定理的逆定理的内容和作用是什么?
判定直角三角形
作用:
逆定理:
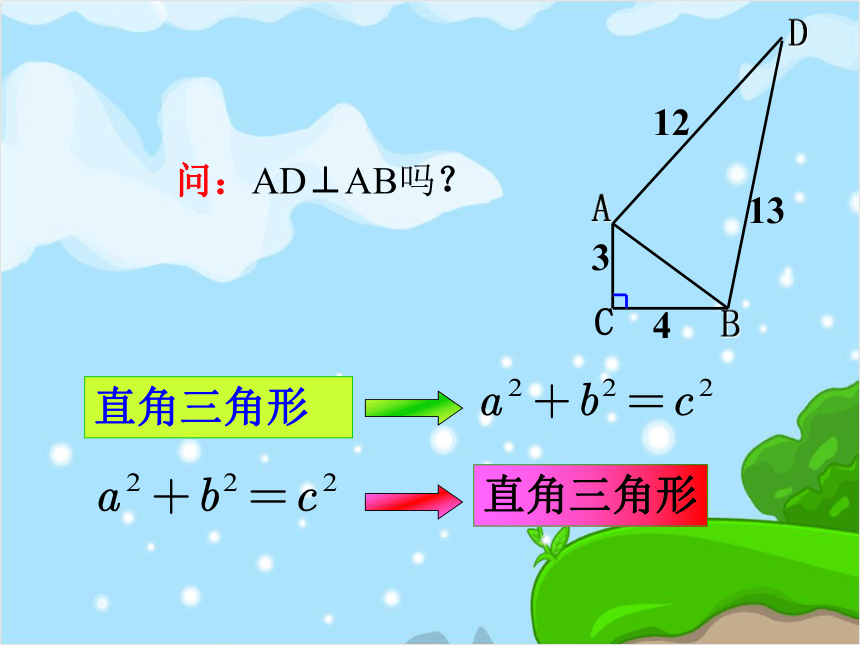
问:AD⊥AB吗?
直角三角形
直角三角形
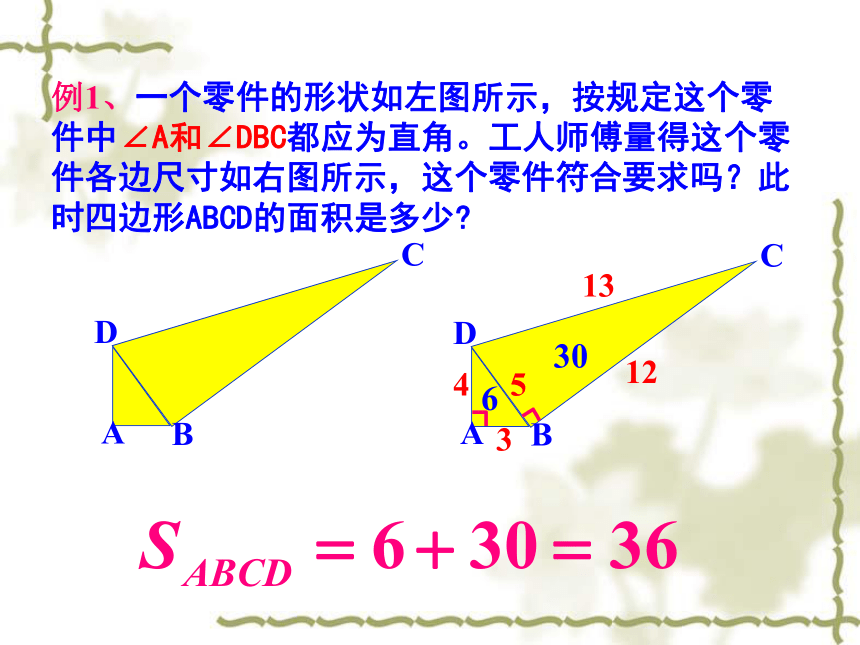
例1、一个零件的形状如左图所示,按规定这个零件中∠A和∠DBC都应为直角。工人师傅量得这个零件各边尺寸如右图所示,这个零件符合要求吗?此时四边形ABCD的面积是多少?
B
C
D
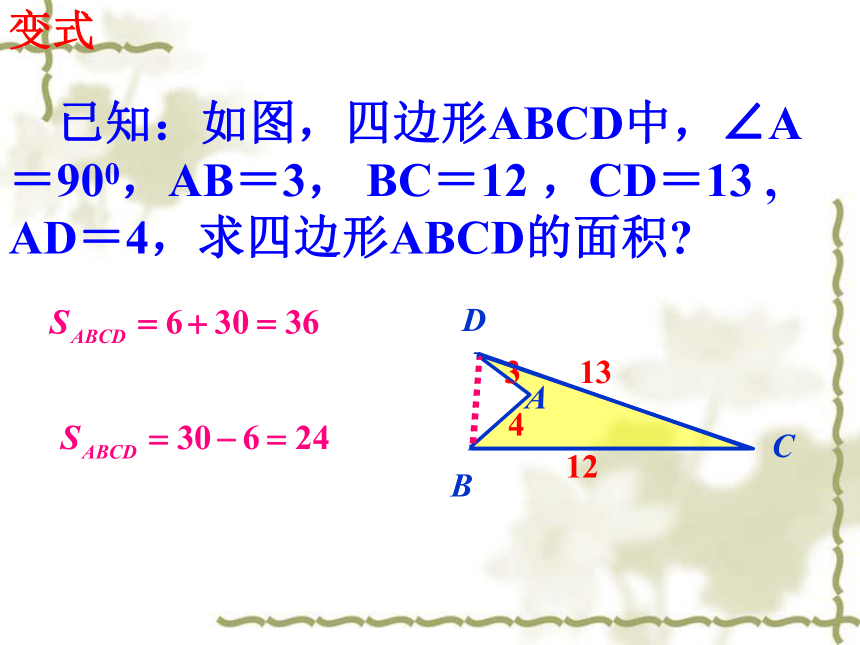
已知:如图,四边形ABCD中,∠A=900,AB=3, BC=12 ,CD=13 , AD=4,求四边形ABCD的面积?
变式
3
12
13
4
A
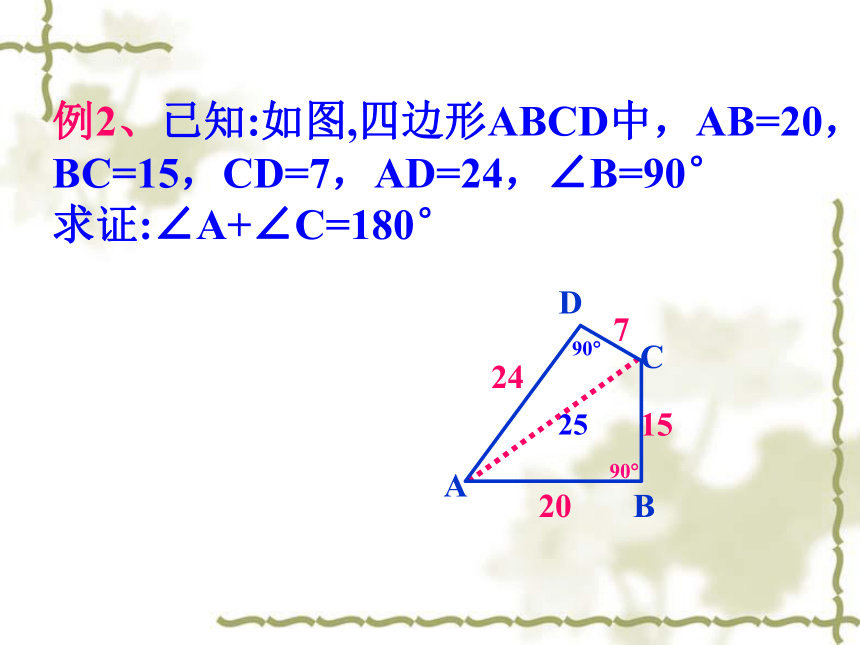
例2、已知:如图,四边形ABCD中,AB=20,BC=15,CD=7,AD=24,∠B=90°
求证:∠A+∠C=180°
A
B
C
D
20
15
7
24
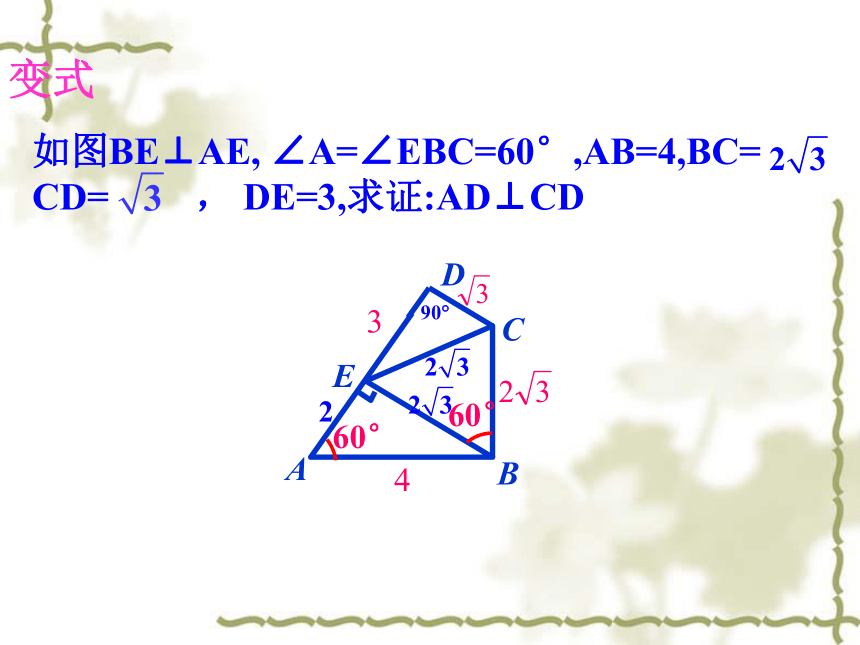
如图BE⊥AE, ∠A=∠EBC=60°,AB=4,BC=
CD= , DE=3,求证:AD⊥CD
变式
A
B
D
C
F
E
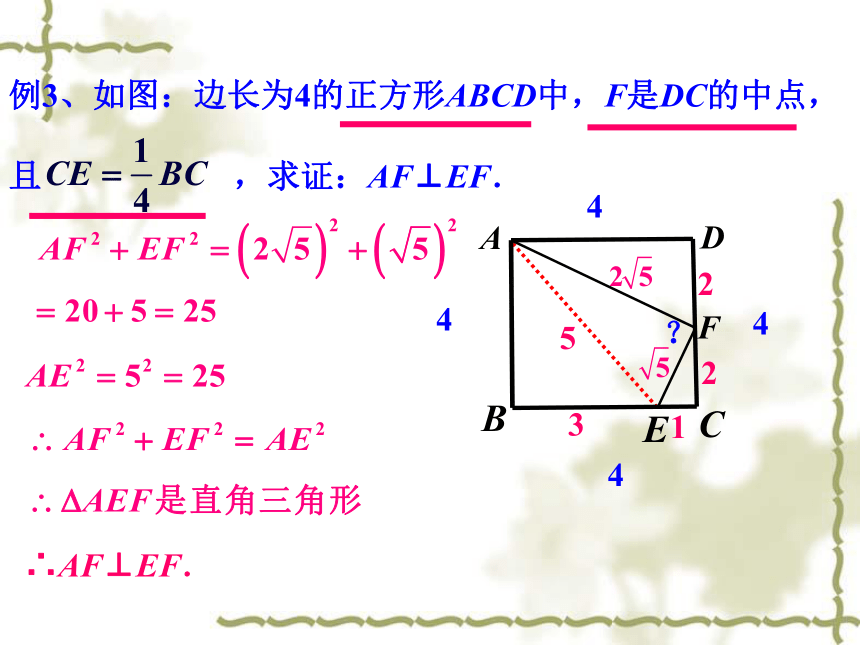
例3、如图:边长为4的正方形ABCD中,F是DC的中点,
且
,求证:AF⊥EF.
4
2
2
4
4
4
1
?
3
5
∴AF⊥EF.
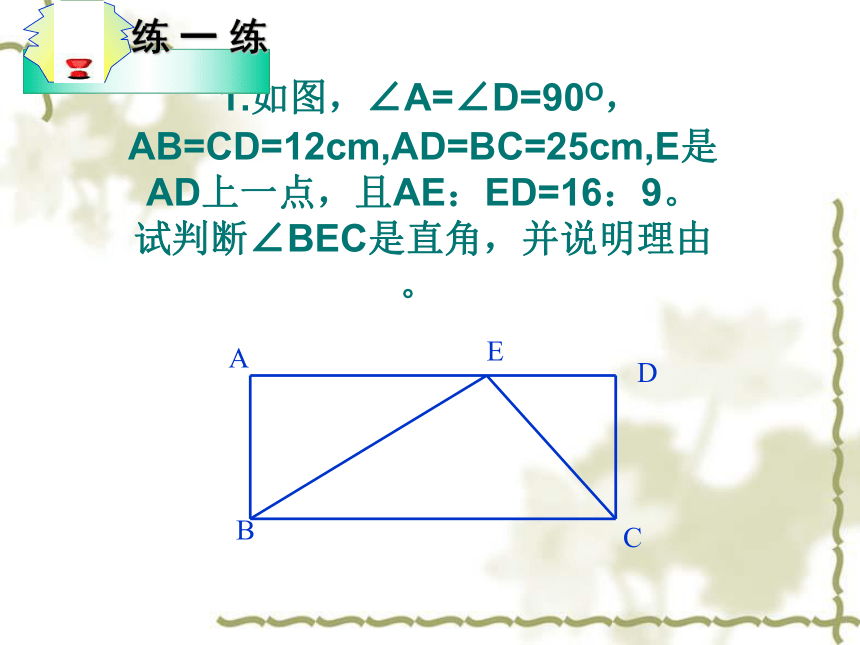
1.如图,∠A=∠D=90O,AB=CD=12cm,AD=BC=25cm,E是AD上一点,且AE:ED=16:9。试判断∠BEC是直角,并说明理由。?
港口
例1、某港口位于东西方向的海岸线上. “远航”号、“海天”号轮船同时离开港口,各自沿一固定方向航行,“远航”号每小时航行16海里,“海天”号每小时航行12海里。它们离开港口一个半小时后相距30海里。如果知道“远航”号沿东北方向航行,能知道“海天”号沿哪个方向航行吗?
P
16×1.5=24
12×1.5=18
30
45°
解:根据题意画图,如图所示:
PQ=16×1.5=24
PR=12×1.5=18
QR=30
∵242+182=302,
即 PQ2+PR2=QR2
∴∠QPR=900
由”远航“号沿东北方向航行可知,∠QPS=450.所以∠RPS=450,
45°
45°
即“海天”号沿西北方向航行.
练、在O处的某海防哨所发现在它的北偏东60°方向相距1000米的A处有一艘快艇正在向正南方向航行,经过若干小时后快艇到达哨所东南方向的B处,
求:(1)此时快艇航行了多少米(即AB 的长)?
(2)距离哨所多少米(即OB的长) ?
1000
A
B
60°
45°
C
500
例 4. 如图,点A是一个半径为 400 m的圆形森林公园的中心,在森林公园附近有 B .C 两个村庄,现要在 B.C 两村庄之间修一条长为 1000 m 的笔直公路将两村连通,经测得 ∠B=60°,∠C=30°,问此公路是否会穿过该森林公园?请通过计算说明.
A
B
C
400
1000
60°
30°
D
如图,点A是一个半径为 400 m的圆形森林公园的中心,在森林公园附近有 B .C 两个村庄,现要在 B.C 两村庄之间修一条长为 1000 m 的笔直公路将两村连通,经测得 AB=600m,AC=800m,问此公路是否会穿过该森林公园?请通过计算说明.
A
B
C
400
1000
D
600
800
变式
(1)城市A是否受到台风影响?
请说明理由。
(2)若城市A受到台风影响,
则持续时间有多长?
(3)城市A受到台风影响的最
大风力为几级?
A
B
30°
C
240
例5:台风是一种自然灾害,它以台风中心为圆心在周围数十千米范围内形成气旋风暴,有极强的破坏力.如图,据气象观测,距沿海城市A的正南方向240千米B处有一台风中心,其中心风力为12级,每远离台风中心25km,风力就会减弱一级。该台风中心现正以20km/h的速度沿北偏东30°方向往C移动,且台风中心风力不变,若城市所受风力达到或超过四级,则称为受台风影响。
A
B
30°
C
240
120
(1)城市A是否受到台风影响?
请说明理由。
A
B
30°
C
240
120
200
200
160
160
(2)若城市A受到台风影响,
则持续时间有多长?
A
B
30°
C
240
120
200
200
160
160
(3)城市A受到台风影响的最
大风力为几级?
例 6 、求证:m2-n2,m2+n2,2mn
(m>n,m,n是正整数)是直角三角形的三条边长。
分析:先来判断m2-n2,m2+n2,2mn三边哪条最长,可以代m,n为满足条件的特殊值来试,如m=5,n=4.则分别为9,40,41, 则m2+n2 最大。
1.已知:在△ABC中,AB=13cm,BC=10cm,BC边上的中线AD=12cm.求证:AB=AC.
A
B
C
D
2. 已知在Rt△ABC中,AC=BC,P为△ABC内一点,且PA=1,PB=3,PC=2,求∠APC的度数.
3.如果△ABC的三边分别为a、b、c且满足
a2+b2+c2+50=6a+8b+10c,
判定△ABC的形状.
(二)解答题:
练 习
这个三角形是直角三角形.
归纳小结
a
c
b
A
B
C
如果三角形两边的平方和等于第三边平方,
那么这个三角形是直角三角形.
直角三角形的判定方法:
60°
45°
75°
B
15°
30°
30°
C
30
30
30°
60
乙船
甲船
甲船
如果三角形的三边长a、b、c满足
a2 + b2 = c2
那么这个三角形是直角三角形。
回顾与思考
勾股定理的逆定理的内容和作用是什么?
判定直角三角形
作用:
逆定理:
问:AD⊥AB吗?
直角三角形
直角三角形
例1、一个零件的形状如左图所示,按规定这个零件中∠A和∠DBC都应为直角。工人师傅量得这个零件各边尺寸如右图所示,这个零件符合要求吗?此时四边形ABCD的面积是多少?
B
C
D
已知:如图,四边形ABCD中,∠A=900,AB=3, BC=12 ,CD=13 , AD=4,求四边形ABCD的面积?
变式
3
12
13
4
A
例2、已知:如图,四边形ABCD中,AB=20,BC=15,CD=7,AD=24,∠B=90°
求证:∠A+∠C=180°
A
B
C
D
20
15
7
24
如图BE⊥AE, ∠A=∠EBC=60°,AB=4,BC=
CD= , DE=3,求证:AD⊥CD
变式
A
B
D
C
F
E
例3、如图:边长为4的正方形ABCD中,F是DC的中点,
且
,求证:AF⊥EF.
4
2
2
4
4
4
1
?
3
5
∴AF⊥EF.
1.如图,∠A=∠D=90O,AB=CD=12cm,AD=BC=25cm,E是AD上一点,且AE:ED=16:9。试判断∠BEC是直角,并说明理由。?
港口
例1、某港口位于东西方向的海岸线上. “远航”号、“海天”号轮船同时离开港口,各自沿一固定方向航行,“远航”号每小时航行16海里,“海天”号每小时航行12海里。它们离开港口一个半小时后相距30海里。如果知道“远航”号沿东北方向航行,能知道“海天”号沿哪个方向航行吗?
P
16×1.5=24
12×1.5=18
30
45°
解:根据题意画图,如图所示:
PQ=16×1.5=24
PR=12×1.5=18
QR=30
∵242+182=302,
即 PQ2+PR2=QR2
∴∠QPR=900
由”远航“号沿东北方向航行可知,∠QPS=450.所以∠RPS=450,
45°
45°
即“海天”号沿西北方向航行.
练、在O处的某海防哨所发现在它的北偏东60°方向相距1000米的A处有一艘快艇正在向正南方向航行,经过若干小时后快艇到达哨所东南方向的B处,
求:(1)此时快艇航行了多少米(即AB 的长)?
(2)距离哨所多少米(即OB的长) ?
1000
A
B
60°
45°
C
500
例 4. 如图,点A是一个半径为 400 m的圆形森林公园的中心,在森林公园附近有 B .C 两个村庄,现要在 B.C 两村庄之间修一条长为 1000 m 的笔直公路将两村连通,经测得 ∠B=60°,∠C=30°,问此公路是否会穿过该森林公园?请通过计算说明.
A
B
C
400
1000
60°
30°
D
如图,点A是一个半径为 400 m的圆形森林公园的中心,在森林公园附近有 B .C 两个村庄,现要在 B.C 两村庄之间修一条长为 1000 m 的笔直公路将两村连通,经测得 AB=600m,AC=800m,问此公路是否会穿过该森林公园?请通过计算说明.
A
B
C
400
1000
D
600
800
变式
(1)城市A是否受到台风影响?
请说明理由。
(2)若城市A受到台风影响,
则持续时间有多长?
(3)城市A受到台风影响的最
大风力为几级?
A
B
30°
C
240
例5:台风是一种自然灾害,它以台风中心为圆心在周围数十千米范围内形成气旋风暴,有极强的破坏力.如图,据气象观测,距沿海城市A的正南方向240千米B处有一台风中心,其中心风力为12级,每远离台风中心25km,风力就会减弱一级。该台风中心现正以20km/h的速度沿北偏东30°方向往C移动,且台风中心风力不变,若城市所受风力达到或超过四级,则称为受台风影响。
A
B
30°
C
240
120
(1)城市A是否受到台风影响?
请说明理由。
A
B
30°
C
240
120
200
200
160
160
(2)若城市A受到台风影响,
则持续时间有多长?
A
B
30°
C
240
120
200
200
160
160
(3)城市A受到台风影响的最
大风力为几级?
例 6 、求证:m2-n2,m2+n2,2mn
(m>n,m,n是正整数)是直角三角形的三条边长。
分析:先来判断m2-n2,m2+n2,2mn三边哪条最长,可以代m,n为满足条件的特殊值来试,如m=5,n=4.则分别为9,40,41, 则m2+n2 最大。
1.已知:在△ABC中,AB=13cm,BC=10cm,BC边上的中线AD=12cm.求证:AB=AC.
A
B
C
D
2. 已知在Rt△ABC中,AC=BC,P为△ABC内一点,且PA=1,PB=3,PC=2,求∠APC的度数.
3.如果△ABC的三边分别为a、b、c且满足
a2+b2+c2+50=6a+8b+10c,
判定△ABC的形状.
(二)解答题:
练 习
这个三角形是直角三角形.
归纳小结
a
c
b
A
B
C
如果三角形两边的平方和等于第三边平方,
那么这个三角形是直角三角形.
直角三角形的判定方法:
60°
45°
75°
B
15°
30°
30°
C
30
30
30°
60
乙船
甲船
甲船
