湘教版八年级数学下册 1.1 直角三角形的性质和判定1课件( 第1课时)
文档属性
| 名称 | 湘教版八年级数学下册 1.1 直角三角形的性质和判定1课件( 第1课时) |

|
|
| 格式 | zip | ||
| 文件大小 | 650.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 湘教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-02-14 00:00:00 | ||
图片预览




文档简介
(共19张PPT)
直角三角形的性质和判定(I)
八年级数学下册(湘教版)
(第一课时)
问题2:直角三角形作为一种特殊的三角形,除了具有一般三角形的性质外,它还会具有哪些特殊的性质?
问题1:小学我们对直角三角形有哪些认识?
01
思考
新知探究
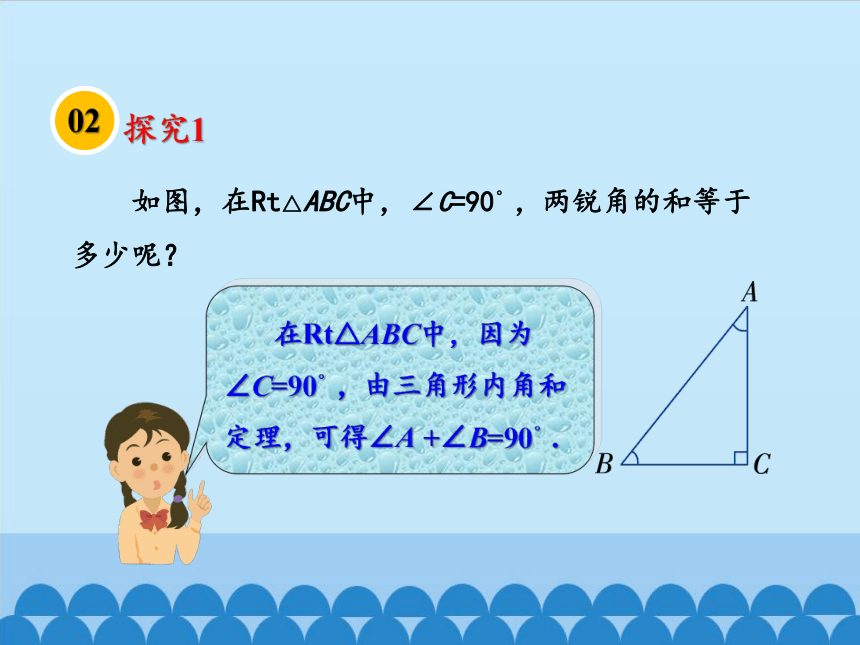
如图,在Rt△ABC中,∠C=90°,两锐角的和等于多少呢?
在Rt△ABC中,因为 ∠C=90°,由三角形内角和定理,可得∠A +∠B=90°.
02
探究1
结论
直角三角形的两个锐角互余.
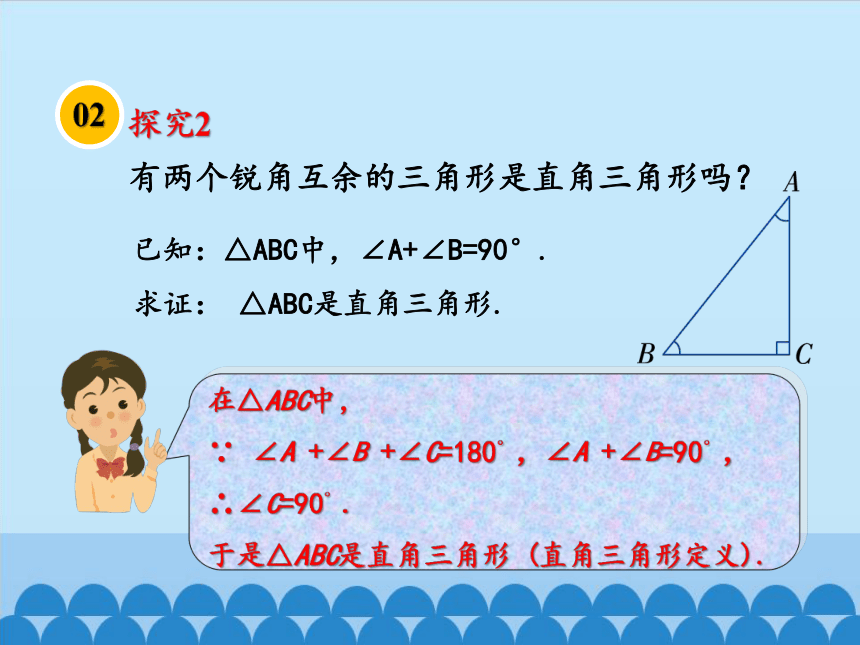
有两个锐角互余的三角形是直角三角形吗?
已知:△ABC中,∠A+∠B=90°.
求证: △ABC是直角三角形.
在△ABC中,
∵ ∠A +∠B +∠C=180°,∠A +∠B=90°,∴∠C=90°.
于是△ABC是直角三角形 (直角三角形定义).
02
探究2
有两个角互余的三角形是直角三角形.
结论
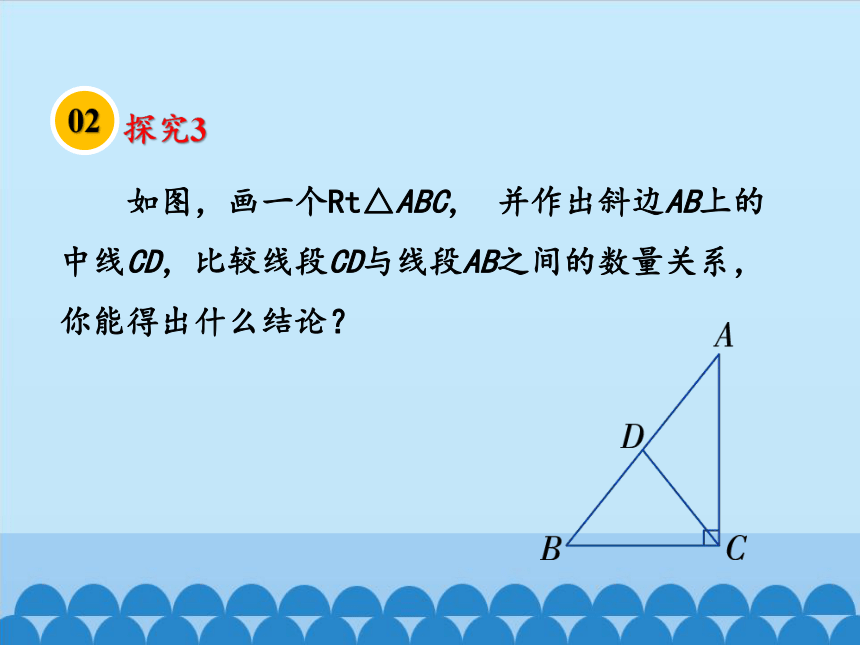
如图,画一个Rt△ABC, 并作出斜边AB上的中线CD,比较线段CD与线段AB之间的数量关系,你能得出什么结论?
02
探究3
线段CD 比线段AB 短.
对于任意一个Rt△ABC,是否都有CD = 成立呢?
我测量后发现CD = AB.
如图,Rt△ABC中,如果中线CD = AB,则CD=BD=AD,于是有∠DCA =∠A .
故作 时,可证得
∠A +∠B=90° ,
又∵
,
∴
∴
故得
∴ 点 是斜边上的中点,即 是斜边 的中线.
从而
CD与 重合,且
Rt△ABC中,过直角顶点C作射线 交AB于 ,使
直角三角形斜边上的中线等于斜边的一半.
这个定理还可以怎么证明?
结论
已知:如图,Rt△ABC中,CD是斜边的中线.
求证:CD= AB.
证明:延长CD到E,使DE=CD,连接BE.
易证△BED≌△ACD.
∴∠BED=∠ACD,BE=AC.
∵Rt△ABC中,∠ACB=∠ACD+∠ECB =90°.
∴∠BED+∠ECB =90°.
∴△BCE是直角三角形.
从而可证△BEC≌△CAB.
∴EC=AB.
∴CD= EC= AB.
例1 如图,已知CD是△ABC的AB边上的中线,且 .
求证:△ABC是直角三角形.
例题精讲
证明:∵ , ∴∠1=∠A,∠2=∠B (等边对等角)
根据三角形内角和性质,有
∠A+∠B+∠ACB =180°,
即得∠A+∠B+∠1+∠2=180°,
∴2(∠A+∠B)=180°.
所以 ∠A+∠B =90°.
∴△ABC是直角三角形
(有一个角是直角的三角形的直角三角形).
分析
先根据两直线平行,同位角相等求出∠3,再根据直角三角形两锐角互余即可求出∠2.
A
1.如图,l1//l2, l3⊥l4 , ∠1=42°,那么∠2的度数( )
A 48° B 42° C 38° D 21°
1
2
l1
l2
l3
l4
3
随堂练习
2.如图所示,在锐角三角形ABC中,CD,BE分别是AB,AC边上的高,且CD,BE交于一点P,若∠A=50°,则∠BPC的度数是( ).
A.150° B.130°
C.120° D.100°
因为BE,CD是ABC的高,
所以∠BDP=90°,∠BEA=90°.
又∠A=50° ,
所以∠ABE=90°-∠A=90°-50°= 40°.
所以∠BPC =∠ABE +∠BDP = 90° + 40°= 130°.
故应选择B.
解
B
练习
1.在Rt△ABC中,斜边上的中线CD=2.5cm ,则斜边 AB的长是多少?
解
AB=2CD=2×2.5=5(cm).
2.如图,AB∥CD,∠BAC和∠ACD的平分线相交于H点,E为AC的中点,EH=2. 那么△AHC是直角三角形吗?为什么?若是,求出AC的长.
解
因为 AB∥CD,所以 ∠BAC+∠DCA=180°.
又 , ,
所以
所以△AHC是直角三角形.
在Rt△AHC中,EH为斜边上的中线,
所以有 ,
由EH=2易知AC=4.
通过本节课,你有什么收获?
你还存在哪些疑问,和同伴交流.
我思 我进步
直角三角形的性质和判定(I)
八年级数学下册(湘教版)
(第一课时)
问题2:直角三角形作为一种特殊的三角形,除了具有一般三角形的性质外,它还会具有哪些特殊的性质?
问题1:小学我们对直角三角形有哪些认识?
01
思考
新知探究
如图,在Rt△ABC中,∠C=90°,两锐角的和等于多少呢?
在Rt△ABC中,因为 ∠C=90°,由三角形内角和定理,可得∠A +∠B=90°.
02
探究1
结论
直角三角形的两个锐角互余.
有两个锐角互余的三角形是直角三角形吗?
已知:△ABC中,∠A+∠B=90°.
求证: △ABC是直角三角形.
在△ABC中,
∵ ∠A +∠B +∠C=180°,∠A +∠B=90°,∴∠C=90°.
于是△ABC是直角三角形 (直角三角形定义).
02
探究2
有两个角互余的三角形是直角三角形.
结论
如图,画一个Rt△ABC, 并作出斜边AB上的中线CD,比较线段CD与线段AB之间的数量关系,你能得出什么结论?
02
探究3
线段CD 比线段AB 短.
对于任意一个Rt△ABC,是否都有CD = 成立呢?
我测量后发现CD = AB.
如图,Rt△ABC中,如果中线CD = AB,则CD=BD=AD,于是有∠DCA =∠A .
故作 时,可证得
∠A +∠B=90° ,
又∵
,
∴
∴
故得
∴ 点 是斜边上的中点,即 是斜边 的中线.
从而
CD与 重合,且
Rt△ABC中,过直角顶点C作射线 交AB于 ,使
直角三角形斜边上的中线等于斜边的一半.
这个定理还可以怎么证明?
结论
已知:如图,Rt△ABC中,CD是斜边的中线.
求证:CD= AB.
证明:延长CD到E,使DE=CD,连接BE.
易证△BED≌△ACD.
∴∠BED=∠ACD,BE=AC.
∵Rt△ABC中,∠ACB=∠ACD+∠ECB =90°.
∴∠BED+∠ECB =90°.
∴△BCE是直角三角形.
从而可证△BEC≌△CAB.
∴EC=AB.
∴CD= EC= AB.
例1 如图,已知CD是△ABC的AB边上的中线,且 .
求证:△ABC是直角三角形.
例题精讲
证明:∵ , ∴∠1=∠A,∠2=∠B (等边对等角)
根据三角形内角和性质,有
∠A+∠B+∠ACB =180°,
即得∠A+∠B+∠1+∠2=180°,
∴2(∠A+∠B)=180°.
所以 ∠A+∠B =90°.
∴△ABC是直角三角形
(有一个角是直角的三角形的直角三角形).
分析
先根据两直线平行,同位角相等求出∠3,再根据直角三角形两锐角互余即可求出∠2.
A
1.如图,l1//l2, l3⊥l4 , ∠1=42°,那么∠2的度数( )
A 48° B 42° C 38° D 21°
1
2
l1
l2
l3
l4
3
随堂练习
2.如图所示,在锐角三角形ABC中,CD,BE分别是AB,AC边上的高,且CD,BE交于一点P,若∠A=50°,则∠BPC的度数是( ).
A.150° B.130°
C.120° D.100°
因为BE,CD是ABC的高,
所以∠BDP=90°,∠BEA=90°.
又∠A=50° ,
所以∠ABE=90°-∠A=90°-50°= 40°.
所以∠BPC =∠ABE +∠BDP = 90° + 40°= 130°.
故应选择B.
解
B
练习
1.在Rt△ABC中,斜边上的中线CD=2.5cm ,则斜边 AB的长是多少?
解
AB=2CD=2×2.5=5(cm).
2.如图,AB∥CD,∠BAC和∠ACD的平分线相交于H点,E为AC的中点,EH=2. 那么△AHC是直角三角形吗?为什么?若是,求出AC的长.
解
因为 AB∥CD,所以 ∠BAC+∠DCA=180°.
又 , ,
所以
所以△AHC是直角三角形.
在Rt△AHC中,EH为斜边上的中线,
所以有 ,
由EH=2易知AC=4.
通过本节课,你有什么收获?
你还存在哪些疑问,和同伴交流.
我思 我进步
同课章节目录
- 第1章 直角三角形
- 1.1 直角三角形的性质与判定(Ⅰ)
- 1.2 直角三角形的性质与判定(Ⅱ)
- 1.3 直角三角形全等的判定
- 1.4 角平分线的性质
- 第2章 四边形
- 2.1 多边形
- 2.2 平行四边形
- 2.3 中心对称和中心对称图形
- 2.4 三角形的中位线
- 2.5 矩形
- 2.6 菱形
- 2.7 正方形
- 第3章 图形与坐标
- 3.1 平面直角坐标系
- 3.2 简单图形的坐标表示
- 3.3 轴对称和平移的坐标表示
- 第4章 一次函数
- 4.1 函数和它的表示法
- 4.2 一次函数
- 4.3 一次函数的图象
- 4.4 用待定系数法确定一次函数表达式
- 4.5 一次函数的应用
- 第5章 数据的频数分布
- 5.1 频数与频率
- 5.2 频数直方图
