湘教版八年级数学下册 1.1直角三角形的性质和判定1课件(第2课时)
文档属性
| 名称 | 湘教版八年级数学下册 1.1直角三角形的性质和判定1课件(第2课时) |

|
|
| 格式 | zip | ||
| 文件大小 | 2.0MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 湘教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-02-14 00:00:00 | ||
图片预览





文档简介
(共17张PPT)
直角三角形的性质和判定(I)
八年级数学下册(湘教版)
(第二课时)
创设情境
在教室布置中,我们需要一些等腰三角形,为了不浪费材料,我们想把上次寝室布置留下的直角三角形余料充分利用起来。
你有一个任意直角三角形纸片,
如何只剪一刀,将它分割成两个等腰三角形?
你能发现含30°锐角的特殊直角三角形有什么性质呢?
合作交流
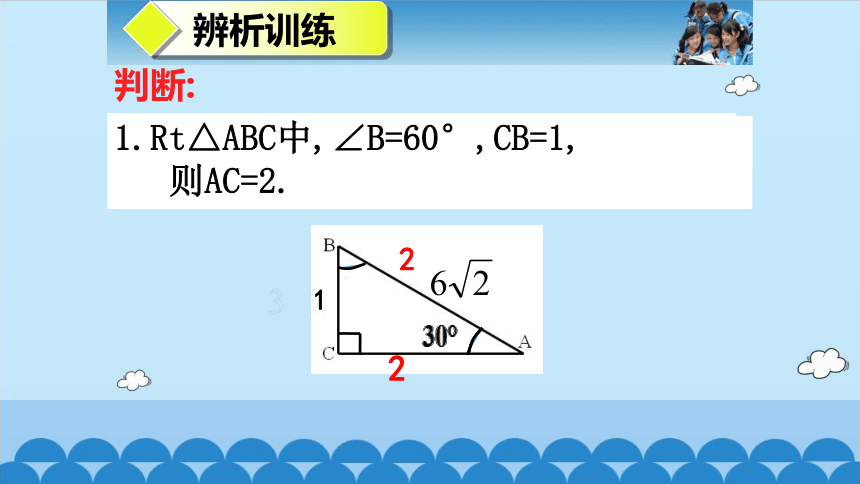
2. △ABC中,∠A=30°,CB=1,则AB=2.
3. Rt△ABC中,∠C=90°,AB= , ∠A=30°,则CB= .
判断:
辨析训练
1
60°
1.Rt△ABC中,∠B=60°,CB=1,
则AC=2.
2
2
Rt△ABC中,∠C=90°,AB= ,
CB= 则∠A=_________.
填空:
思考:
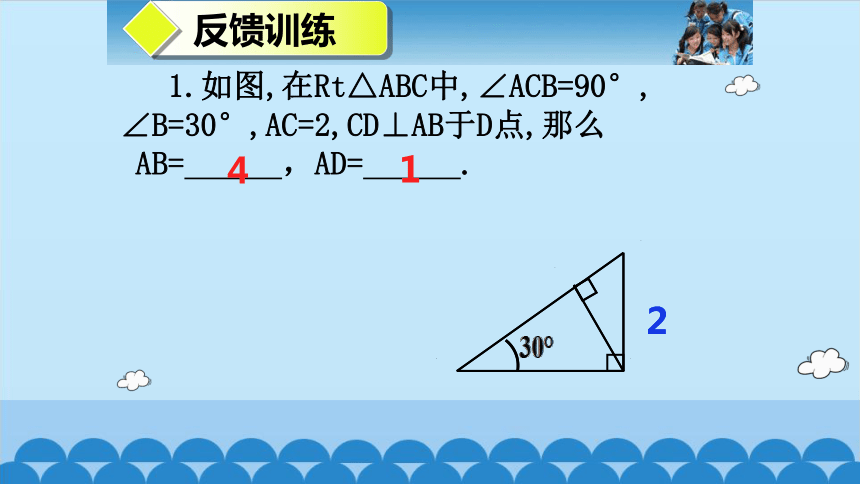
1.如图,在Rt△ABC中,∠ACB=90°,
∠B=30°,AC=2,CD⊥AB于D点,那么
AB= ,AD= .
反馈训练
4
1
2
A
B
C
D
2
A
B
C
D
反馈训练
2、如图, 在Rt△ABC中, ∠ACB=90°, CD⊥AB于点D, BD=2,BC=4
则∠BCD= _______,AD=_______.
2
4
如图,在A岛周围20海里水域内有暗礁, 一轮船由西向东航行到O处时, 测得A岛在北偏东60°的方向, 且与轮船相距 海里. 若该船继续保持航向不变,
那么有触礁的危险吗?
典例精析
B
O
C
D
A
该轮船由西向东航行到A岛的正南方向D点,无触礁危险,继续航行15海里到E点时,测得A岛与E点相距30海里,那么此时海岛A位于E点的( )
E
A
变式训练
30
15
D
B
O
A.北偏西60°
B.北偏西30°
C.南偏东60°
D.南偏东30°
(教材第8页第8题)
如图,小芳在山下发现正前方山上有个电视塔,测得塔尖的仰角为15°,小芳朝正前方笔直行走400m,此时测得塔尖的仰角为30°.若小芳的眼睛离地面1.6m,你能算出这个电视塔塔尖离地面的高度吗?
针对训练
O
(1)这节课我们对直角三角形有哪些
新的认识?
(2)从研究方法上你有哪些收获?
小结反思
小结反思
在前面的讨论中,如果把直角三角形,30度角所对的边,这条边等于最长边的一半,分别看成三个要素,能不能任选其中两个要素,证明另一个要素的成立呢?
1.如图,在Rt△ABC中,∠C=90°, ∠B=30°, ∠AFC=45°,AB=12cm,
则△ACF的面积= cm2.
巩固练习
2、已知,如图AB=6, AC=4,
△ABC的面积为6,
则∠A = .
巩固练习
D
巩固练习
E
2、已知,如图AB=6, AC=4,
△ABC的面积为6,
则∠A = .
3
巩固练习
3、如图, 在Rt△ABC中, ∠ACB=90°, ∠B=30°,AB=2,CD是斜边上的中线,
CE是高,F是CD的中点.
(1)求CD的长
(2)证明:
△EDF为等边三角形
2
直角三角形的性质和判定(I)
八年级数学下册(湘教版)
(第二课时)
创设情境
在教室布置中,我们需要一些等腰三角形,为了不浪费材料,我们想把上次寝室布置留下的直角三角形余料充分利用起来。
你有一个任意直角三角形纸片,
如何只剪一刀,将它分割成两个等腰三角形?
你能发现含30°锐角的特殊直角三角形有什么性质呢?
合作交流
2. △ABC中,∠A=30°,CB=1,则AB=2.
3. Rt△ABC中,∠C=90°,AB= , ∠A=30°,则CB= .
判断:
辨析训练
1
60°
1.Rt△ABC中,∠B=60°,CB=1,
则AC=2.
2
2
Rt△ABC中,∠C=90°,AB= ,
CB= 则∠A=_________.
填空:
思考:
1.如图,在Rt△ABC中,∠ACB=90°,
∠B=30°,AC=2,CD⊥AB于D点,那么
AB= ,AD= .
反馈训练
4
1
2
A
B
C
D
2
A
B
C
D
反馈训练
2、如图, 在Rt△ABC中, ∠ACB=90°, CD⊥AB于点D, BD=2,BC=4
则∠BCD= _______,AD=_______.
2
4
如图,在A岛周围20海里水域内有暗礁, 一轮船由西向东航行到O处时, 测得A岛在北偏东60°的方向, 且与轮船相距 海里. 若该船继续保持航向不变,
那么有触礁的危险吗?
典例精析
B
O
C
D
A
该轮船由西向东航行到A岛的正南方向D点,无触礁危险,继续航行15海里到E点时,测得A岛与E点相距30海里,那么此时海岛A位于E点的( )
E
A
变式训练
30
15
D
B
O
A.北偏西60°
B.北偏西30°
C.南偏东60°
D.南偏东30°
(教材第8页第8题)
如图,小芳在山下发现正前方山上有个电视塔,测得塔尖的仰角为15°,小芳朝正前方笔直行走400m,此时测得塔尖的仰角为30°.若小芳的眼睛离地面1.6m,你能算出这个电视塔塔尖离地面的高度吗?
针对训练
O
(1)这节课我们对直角三角形有哪些
新的认识?
(2)从研究方法上你有哪些收获?
小结反思
小结反思
在前面的讨论中,如果把直角三角形,30度角所对的边,这条边等于最长边的一半,分别看成三个要素,能不能任选其中两个要素,证明另一个要素的成立呢?
1.如图,在Rt△ABC中,∠C=90°, ∠B=30°, ∠AFC=45°,AB=12cm,
则△ACF的面积= cm2.
巩固练习
2、已知,如图AB=6, AC=4,
△ABC的面积为6,
则∠A = .
巩固练习
D
巩固练习
E
2、已知,如图AB=6, AC=4,
△ABC的面积为6,
则∠A = .
3
巩固练习
3、如图, 在Rt△ABC中, ∠ACB=90°, ∠B=30°,AB=2,CD是斜边上的中线,
CE是高,F是CD的中点.
(1)求CD的长
(2)证明:
△EDF为等边三角形
2
同课章节目录
- 第1章 直角三角形
- 1.1 直角三角形的性质与判定(Ⅰ)
- 1.2 直角三角形的性质与判定(Ⅱ)
- 1.3 直角三角形全等的判定
- 1.4 角平分线的性质
- 第2章 四边形
- 2.1 多边形
- 2.2 平行四边形
- 2.3 中心对称和中心对称图形
- 2.4 三角形的中位线
- 2.5 矩形
- 2.6 菱形
- 2.7 正方形
- 第3章 图形与坐标
- 3.1 平面直角坐标系
- 3.2 简单图形的坐标表示
- 3.3 轴对称和平移的坐标表示
- 第4章 一次函数
- 4.1 函数和它的表示法
- 4.2 一次函数
- 4.3 一次函数的图象
- 4.4 用待定系数法确定一次函数表达式
- 4.5 一次函数的应用
- 第5章 数据的频数分布
- 5.1 频数与频率
- 5.2 频数直方图
