【北师大版七年级数学下册同步训练】4.4 用尺规作三角形同步训练(含解析)
文档属性
| 名称 | 【北师大版七年级数学下册同步训练】4.4 用尺规作三角形同步训练(含解析) |  | |
| 格式 | zip | ||
| 文件大小 | 524.3KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-02-14 11:12:58 | ||
图片预览




文档简介
4.4用尺规作三角形同步训练
学校:___________姓名:___________班级:___________考号:___________
一、单选题
1.如图是作的作图痕迹,则此作图的已知条件是( )
A.已知两边及夹角 B.已知三边 C.已知两角及夹边 D.已知两边及一边对角
2.如图,小王做试题时,不小心把题目中的三角形用墨水弄污了一部分,他想在一张白纸上作一个完全一样的三角形,然后粘贴在上面,他作图的依据是( )
A. B. C. D.
3.尺规作图作的平分线方法如下:以为圆心,任意长为半径画弧交、于、,再分别以点、为圆心,以大于长为半径画弧,两弧交于点,作射线由作法得的根据是( )
A.SAS B.ASA C.AAS D.SSS
4.用直尺和圆规作两个全等三角形,如图,能得到△COD≌△C'O'D'的依据是( )
A.SAA B.SSS C.ASA D.AAS
5.如图是5×5的正方形网络,以点D,E为两个顶点作位置不同的格点三角形,使所作的格点三角形与△ABC全等,这样的格点三角形最多可以画出( )
A.2个 B.4个 C.6个 D.8个
6.根据下列已知条件,能画出唯一△ABC的是( )
A.AB=3,BC=4,AC=8 B.∠A=100°,∠B=45°,AB=5
C.AB=3,BC=5,∠A=75° D.∠C=90°,∠A=30°,∠B=60°
7.根据下列已知条件,能够画出唯一△ABC 的是( )
A.AB=6,BC=5,∠A=50° B.AB=5,BC=6,AC=13
C.∠A=50°,∠B=80°,AB=8 D.∠A=40°,∠B=50°,∠C=90°
8.用直尺和圆规作一个角的平分线的示意图如图所示,则能说明的依据是( )
A.SSS B.ASA C.AAS D.以上都不对
二、填空题
9.阅读下面材料:
数学课上,老师提出如下问题:
小明解答如右图所示,其中他所画的弧MN是以E为圆心,以CD长为半径的弧
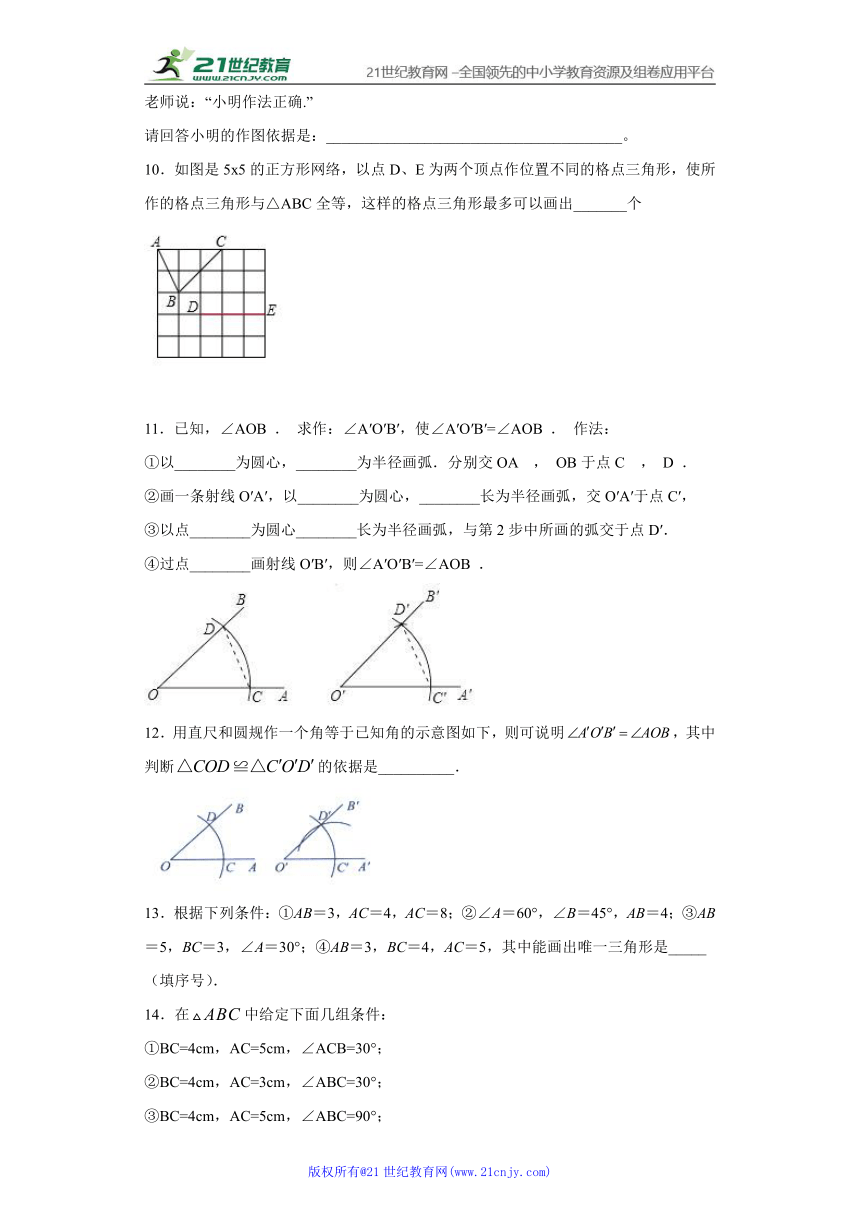
老师说:“小明作法正确.”
请回答小明的作图依据是:_______________________________________。
10.如图是5x5的正方形网络,以点D、E为两个顶点作位置不同的格点三角形,使所作的格点三角形与△ABC全等,这样的格点三角形最多可以画出_______个
11.已知,∠AOB . 求作:∠A′O′B′,使∠A′O′B′=∠AOB . 作法:
①以________为圆心,________为半径画弧.分别交OA , OB于点C , D .
②画一条射线O′A′,以________为圆心,________长为半径画弧,交O′A′于点C′,
③以点________为圆心________长为半径画弧,与第2步中所画的弧交于点D′.
④过点________画射线O′B′,则∠A′O′B′=∠AOB .
12.用直尺和圆规作一个角等于已知角的示意图如下,则可说明,其中判断的依据是__________.
13.根据下列条件:①AB=3,AC=4,AC=8;②∠A=60°,∠B=45°,AB=4;③AB=5,BC=3,∠A=30°;④AB=3,BC=4,AC=5,其中能画出唯一三角形是_____(填序号).
14.在中给定下面几组条件:
①BC=4cm,AC=5cm,∠ACB=30°;
②BC=4cm,AC=3cm,∠ABC=30°;
③BC=4cm,AC=5cm,∠ABC=90°;
④BC=4cm,AC=5cm,∠ABC=120°.
若根据每组条件画图,则能够唯一确定的是___________(填序号).
三、解答题
15.尺规作图:
已知:.求作:,使与全等.
要求:(1)不写作法,保留作图痕迹;
(2)写出作图时选取的相等的边或角.
16.已知:如图,,点是延长线上的一点,且.
求作:,使,且点与点在同侧.(要求:尺规作图,保留作图痕迹)
17.如图,已知∠α和∠β,线段c,用直尺和圆规作出△ABC,使∠A=∠α,∠B=∠β,AB=c(要求画出图形,并保留作图痕迹,不必写出作法)
18.下面是小明设计的“已知两线段及一角作三角形”的尺规作图过程.
已知:线段,及∠O .
求作:△ABC,使得线段,及∠O分别是它的两边和一角.
作法:如图,
①以点O为圆心,长为半径画弧,分别交∠O的两边于点M ,N;
②画一条射线AP,以点A为圆心,长为半径画弧,交AP于点B;
③以点B为圆心,MN长为半径画弧,与第②步中所画的弧相交于点D;
④画射线AD;
⑤以点A为圆心,长为半径画弧,交AD于点C;
⑥连接BC ,则△ABC即为所求作的三角形.
请回答:
(1)步骤③得到两条线段相等,即 = ;
(2)∠A=∠O的作图依据是 ;
(3)小红说小明的作图不全面,原因是 .
参考答案
1.C
【解析】
【分析】
观察的作图痕迹,可得此作图的条件.
【详解】
解:观察的作图痕迹,可得此作图的已知条件为:∠α,∠β,及线段AB,
故已知条件为:两角及夹边,
故选C.
【点睛】
本题主要考查三角形作图及三角形全等的相关知识.
2.C
【解析】
试题解析:图中的三角形已知一条边以及两个角,则他作图的依据是ASA.
故选C.
3.D
【解析】
解:以O为圆心,任意长为半径画弧交OA,OB于C,D,即OC=OD;
以点C,D为圆心,以大于CD长为半径画弧,两弧交于点P,即CP=DP;
再有公共边OP,根据“SSS”即得△OCP≌△ODP.
故选D.
4.B
【解析】
【分析】
利用作法可以得到OD=OD′=OC=OC′,CD=C′D′,然后根据全等三角形的判定方法可判断△COD≌△C'O'D'.
【详解】
解:由作法得OD=OD′=OC=OC′,CD=C′D′,
所以可根据“SSS”证明△COD≌△C'O'D'.
故选:B.
【点睛】
本题考查作图-复杂作图:复杂作图是在五种基本作图的基础上进行作图,一般是结合了几何图形的性质和基本作图方法.也考查了全等三角形的判定.
5.B
【解析】
试题分析:观察图形可知:DE与AC是对应边,B点的对应点在DE上方两个,在DE下方两个共有4个满足要求的点,也就有四个全等三角形.
根据题意,运用SSS可得与△ABC全等的三角形有4个,线段DE的上方有两个点,下方也有两个点.
故选B.
考点:本题考查三角形全等的判定方法
点评:解答本题的关键是按照顺序分析,要做到不重不漏.
6.B
【解析】
【分析】
利用全等三角形的判定方法以及三角形三边关系分别判断得出即可.
【详解】
解:A、3+4<8,不符合三角形三边关系定理,不能画出三角形,故本选项错误;
B、根据∠A=100°,∠B=45°,AB=5能画出唯一△ABC,故此选项正确;
C、AB=3,BC=5,∠A=75°,不能画出唯一三角形,故本选项错误
D、∠C=90°,∠A=30°,∠B=60°,不能画出唯一三角形,故本选项错误;
故选:B.
【点睛】
此题主要考查了全等三角形的判定以及三角形三边关系,正确把握全等三角形的判定方法是解题关键.
7.C
【解析】
【分析】
根据全等三角形的判定方法依次判断各项后即可解答.
【详解】
选项A,已知 AB、BC 和 BC 的对角,不能画出唯一三角形;
选项B,∵AB+BC=5+6=11<AC,∴不能画出△ABC;
选项C,已知两角和夹边,能画出唯一△ABC;
选项D,根据∠A=40°,∠B=50°,∠C=90°不能画出唯一三角形.
故选C.
【点睛】
本题考查了全等三角形的判定方法,一般三角形全等的判定方法有 SSS、SAS、ASA、AAS,熟练掌握全等三角形的判定方法是解题的关键.
8.A
【解析】
【分析】
连接NC,MC,根据SSS证△ONC≌△OMC,即可推出答案.
【详解】
解:连接NC,MC, 在△ONC和△OMC中
∴△ONC≌△OMC(SSS), ∴∠AOC=∠BOC, 故选:A.
【点睛】
本题考查了全等三角形的性质和判定的应用,培养学生运用性质进行推理的能力,题型较好,难度适中.
9.边边边定理证明两个三角形全等,则它们的对应角相等
【解析】
【分析】
由作图过程可知,根据边边边定理证明OCD≌BME,可得.
【详解】
解:以B点为圆心,OC为半径画弧EM交BO于E,以E点为圆心,DC为半径画弧交弧EM于N, 由此过程可知
OCD≌BME(SSS)
故答案为:边边边定理证明两个三角形全等,则它们的对应角相等
【点睛】
本题考查了作一个角等于已知角的作图依据,正确理解作图过程是解题的关键.
10.4
【解析】
【分析】
由图可知,DE与AC是对应边,则B点的对应点在DE上方两个,在DE下方两个共有4个满足要求的点,也就有四个全等三角形.
【详解】
解:根据题意,DE与AC是对应边,则B点的对应点在DE的上方有两个点,下方也有两个点.如图:
故答案为4.
【点睛】
本题考查三角形全等的判定方法关键在于作图寻找全等三角形,做图时要做到不重不漏.
11.O 任意长 O′ OC C CD D′
【解析】
【分析】
根据作一个角等于已知角的作图方法解答即可.
【详解】
①以O为圆心,任意长为半径画弧.分别交OA , OB于点C、D .
②画一条射线O′A′,以O′为圆心,OC长为半径画弧,交O′A′于点C′,
③以点C为圆心CD长为半径画弧,与第2步中所画的弧交于点D′.
④过点D′画射线O′B′,则∠A′O′B′=∠AOB.
故答案为:(1). O; (2). 任意长;(3). O′; (4). OC; (5). C ; (6). CD ;(7). D′
【点睛】
本题主要考查了作一个角等于已知角,是基本作图,需熟练掌握.
12.
【解析】
【分析】
利用作法得到△C'O'D'和△COD的三边对应相等,从而根据SSS可证明△C'O'D'≌△COD,然后根据全等三角形的性质得到∠A'0'B'=∠A0B.
【详解】
解:由作法得0D=0C=0D'=OC',CD=C'D',则根据“SSS”可判断△C'O'D≌△COD,所以∠A'0'B'=∠A0B.
故答案:SSS.
【点睛】
本题考查了作图-基本作图:熟练掌握基本作图(作一条线段等于已知线段;作一个角等于已知角;作已知线段的垂直平分线;作已知角的角平分线;过一点作已知直线的垂线).也考查了角平分线的性质定理的逆定理.
13.②④
【解析】
【分析】
根据三角形的三边关系定理,先看看能否组成三角形,再根据全等三角形的判定定理判断即可.
【详解】
解:①∵3+4<8,∴根据AB=3,BC=4,AB=8不能画出三角形,故本选项错误;
②根据∠A=60°,∠B=30°,AB=4,符合全等三角形的判定定理ASA,即能画出唯一三角形,故本选项正确;
③根据AB=5,BC=3,∠A=30°不能画出唯一三角形,故本选项错误;
④根据AB=3,BC=4,AC=5,符合全等三角形的判定定理SSS,即能画出唯一三角形,故本选项正确;
故答案为:②④.
【点睛】
本题考查了三角形的三边关系定理和全等三角形的判定定理,注意:全等三角形的判定定理有SAS,ASA,AAS,SSS.
14.①③④
【解析】
【分析】
根据全等三角形的判定方法进行分析,从而得到答案.
【详解】
解:①符合全等三角形的判定定理SAS,即能画出唯一三角形,正确; ②根据BC=4cm,AC=3cm,∠ABC=30°不能画出唯一三角形,如图所示△ABC和△BCD, 错误;
③符合全等三角形的判定定理HL,即能画出唯一三角形,正确; ④∵∠ABC为钝角,结合②可知,只能画出唯一三角形,正确. 故答案为:①③④.
【点睛】
本题考查的是全等三角形的判定方法;解答此题的关键是要掌握三角形全等判定的几种方法即可,结合已知逐个验证,要找准对应关系.
15.见解析
【解析】
【分析】
利用全等三角形的判定定理SSS、AAS、ASA、SAS之一来作,作线段B′C′=BC,分别以B′、C′为圆心,BA,CA为半径画弧,两弧交于点A′,连接A′B′,A′C′.(答案不唯一)
【详解】
解:选取AB、BC、AC作图,使其分别等于A′B′、B′C′、A′C′,
如图,即为所作三角形:
【点睛】
本题考查作图-复杂作图,全等三角形的判定等知识,解题的关键是熟练掌握基本知识,属于中考常考题型.
16.见解析
【解析】
【分析】
利用SSS定理,分别以C,D为圆心,以AB,CA长为半径作弧交于点E,连接CE,DE即可得到.
【详解】
解:如图,即为所求作的三角形.
(作法不唯一)
【点睛】
本题考查了全等三角形和作图,关键是掌握全等三角形的判定定理.
17.详见解析.
【解析】
试题分析:先作∠MAN=α,再在AM上取AB=c,再以B为顶点作∠ABC=β,两角的一边交于点C,△ABC就是所求三角形.
试题解析:如图,△ABC就是所求三角形.
考点:尺规作图
18.(1)BD,MN; (2)三边对应相等的两个三角形全等;全等三角形的对应角相等;(3)小明没有对已知中的边和角的位置关系分类讨论.
【解析】
【分析】
根据题意,按步骤解答即可.
【详解】
(1)BD,MN;
(2)三边对应相等的两个三角形全等;全等三角形的对应角相等;
(3)小明没有对已知中的边和角的位置关系分类讨论.
【点睛】
本题考查了作图-复杂作图:复杂作图是在五种基本作图的基础上进行作图,一般是结合了几何图形的性质和基本作图方法.解决此类题目的关键是熟悉基本几何图形的性质,结合几何图形的基本性质把复杂作图拆解成基本作图,逐步操作.
学校:___________姓名:___________班级:___________考号:___________
一、单选题
1.如图是作的作图痕迹,则此作图的已知条件是( )
A.已知两边及夹角 B.已知三边 C.已知两角及夹边 D.已知两边及一边对角
2.如图,小王做试题时,不小心把题目中的三角形用墨水弄污了一部分,他想在一张白纸上作一个完全一样的三角形,然后粘贴在上面,他作图的依据是( )
A. B. C. D.
3.尺规作图作的平分线方法如下:以为圆心,任意长为半径画弧交、于、,再分别以点、为圆心,以大于长为半径画弧,两弧交于点,作射线由作法得的根据是( )
A.SAS B.ASA C.AAS D.SSS
4.用直尺和圆规作两个全等三角形,如图,能得到△COD≌△C'O'D'的依据是( )
A.SAA B.SSS C.ASA D.AAS
5.如图是5×5的正方形网络,以点D,E为两个顶点作位置不同的格点三角形,使所作的格点三角形与△ABC全等,这样的格点三角形最多可以画出( )
A.2个 B.4个 C.6个 D.8个
6.根据下列已知条件,能画出唯一△ABC的是( )
A.AB=3,BC=4,AC=8 B.∠A=100°,∠B=45°,AB=5
C.AB=3,BC=5,∠A=75° D.∠C=90°,∠A=30°,∠B=60°
7.根据下列已知条件,能够画出唯一△ABC 的是( )
A.AB=6,BC=5,∠A=50° B.AB=5,BC=6,AC=13
C.∠A=50°,∠B=80°,AB=8 D.∠A=40°,∠B=50°,∠C=90°
8.用直尺和圆规作一个角的平分线的示意图如图所示,则能说明的依据是( )
A.SSS B.ASA C.AAS D.以上都不对
二、填空题
9.阅读下面材料:
数学课上,老师提出如下问题:
小明解答如右图所示,其中他所画的弧MN是以E为圆心,以CD长为半径的弧
老师说:“小明作法正确.”
请回答小明的作图依据是:_______________________________________。
10.如图是5x5的正方形网络,以点D、E为两个顶点作位置不同的格点三角形,使所作的格点三角形与△ABC全等,这样的格点三角形最多可以画出_______个
11.已知,∠AOB . 求作:∠A′O′B′,使∠A′O′B′=∠AOB . 作法:
①以________为圆心,________为半径画弧.分别交OA , OB于点C , D .
②画一条射线O′A′,以________为圆心,________长为半径画弧,交O′A′于点C′,
③以点________为圆心________长为半径画弧,与第2步中所画的弧交于点D′.
④过点________画射线O′B′,则∠A′O′B′=∠AOB .
12.用直尺和圆规作一个角等于已知角的示意图如下,则可说明,其中判断的依据是__________.
13.根据下列条件:①AB=3,AC=4,AC=8;②∠A=60°,∠B=45°,AB=4;③AB=5,BC=3,∠A=30°;④AB=3,BC=4,AC=5,其中能画出唯一三角形是_____(填序号).
14.在中给定下面几组条件:
①BC=4cm,AC=5cm,∠ACB=30°;
②BC=4cm,AC=3cm,∠ABC=30°;
③BC=4cm,AC=5cm,∠ABC=90°;
④BC=4cm,AC=5cm,∠ABC=120°.
若根据每组条件画图,则能够唯一确定的是___________(填序号).
三、解答题
15.尺规作图:
已知:.求作:,使与全等.
要求:(1)不写作法,保留作图痕迹;
(2)写出作图时选取的相等的边或角.
16.已知:如图,,点是延长线上的一点,且.
求作:,使,且点与点在同侧.(要求:尺规作图,保留作图痕迹)
17.如图,已知∠α和∠β,线段c,用直尺和圆规作出△ABC,使∠A=∠α,∠B=∠β,AB=c(要求画出图形,并保留作图痕迹,不必写出作法)
18.下面是小明设计的“已知两线段及一角作三角形”的尺规作图过程.
已知:线段,及∠O .
求作:△ABC,使得线段,及∠O分别是它的两边和一角.
作法:如图,
①以点O为圆心,长为半径画弧,分别交∠O的两边于点M ,N;
②画一条射线AP,以点A为圆心,长为半径画弧,交AP于点B;
③以点B为圆心,MN长为半径画弧,与第②步中所画的弧相交于点D;
④画射线AD;
⑤以点A为圆心,长为半径画弧,交AD于点C;
⑥连接BC ,则△ABC即为所求作的三角形.
请回答:
(1)步骤③得到两条线段相等,即 = ;
(2)∠A=∠O的作图依据是 ;
(3)小红说小明的作图不全面,原因是 .
参考答案
1.C
【解析】
【分析】
观察的作图痕迹,可得此作图的条件.
【详解】
解:观察的作图痕迹,可得此作图的已知条件为:∠α,∠β,及线段AB,
故已知条件为:两角及夹边,
故选C.
【点睛】
本题主要考查三角形作图及三角形全等的相关知识.
2.C
【解析】
试题解析:图中的三角形已知一条边以及两个角,则他作图的依据是ASA.
故选C.
3.D
【解析】
解:以O为圆心,任意长为半径画弧交OA,OB于C,D,即OC=OD;
以点C,D为圆心,以大于CD长为半径画弧,两弧交于点P,即CP=DP;
再有公共边OP,根据“SSS”即得△OCP≌△ODP.
故选D.
4.B
【解析】
【分析】
利用作法可以得到OD=OD′=OC=OC′,CD=C′D′,然后根据全等三角形的判定方法可判断△COD≌△C'O'D'.
【详解】
解:由作法得OD=OD′=OC=OC′,CD=C′D′,
所以可根据“SSS”证明△COD≌△C'O'D'.
故选:B.
【点睛】
本题考查作图-复杂作图:复杂作图是在五种基本作图的基础上进行作图,一般是结合了几何图形的性质和基本作图方法.也考查了全等三角形的判定.
5.B
【解析】
试题分析:观察图形可知:DE与AC是对应边,B点的对应点在DE上方两个,在DE下方两个共有4个满足要求的点,也就有四个全等三角形.
根据题意,运用SSS可得与△ABC全等的三角形有4个,线段DE的上方有两个点,下方也有两个点.
故选B.
考点:本题考查三角形全等的判定方法
点评:解答本题的关键是按照顺序分析,要做到不重不漏.
6.B
【解析】
【分析】
利用全等三角形的判定方法以及三角形三边关系分别判断得出即可.
【详解】
解:A、3+4<8,不符合三角形三边关系定理,不能画出三角形,故本选项错误;
B、根据∠A=100°,∠B=45°,AB=5能画出唯一△ABC,故此选项正确;
C、AB=3,BC=5,∠A=75°,不能画出唯一三角形,故本选项错误
D、∠C=90°,∠A=30°,∠B=60°,不能画出唯一三角形,故本选项错误;
故选:B.
【点睛】
此题主要考查了全等三角形的判定以及三角形三边关系,正确把握全等三角形的判定方法是解题关键.
7.C
【解析】
【分析】
根据全等三角形的判定方法依次判断各项后即可解答.
【详解】
选项A,已知 AB、BC 和 BC 的对角,不能画出唯一三角形;
选项B,∵AB+BC=5+6=11<AC,∴不能画出△ABC;
选项C,已知两角和夹边,能画出唯一△ABC;
选项D,根据∠A=40°,∠B=50°,∠C=90°不能画出唯一三角形.
故选C.
【点睛】
本题考查了全等三角形的判定方法,一般三角形全等的判定方法有 SSS、SAS、ASA、AAS,熟练掌握全等三角形的判定方法是解题的关键.
8.A
【解析】
【分析】
连接NC,MC,根据SSS证△ONC≌△OMC,即可推出答案.
【详解】
解:连接NC,MC, 在△ONC和△OMC中
∴△ONC≌△OMC(SSS), ∴∠AOC=∠BOC, 故选:A.
【点睛】
本题考查了全等三角形的性质和判定的应用,培养学生运用性质进行推理的能力,题型较好,难度适中.
9.边边边定理证明两个三角形全等,则它们的对应角相等
【解析】
【分析】
由作图过程可知,根据边边边定理证明OCD≌BME,可得.
【详解】
解:以B点为圆心,OC为半径画弧EM交BO于E,以E点为圆心,DC为半径画弧交弧EM于N, 由此过程可知
OCD≌BME(SSS)
故答案为:边边边定理证明两个三角形全等,则它们的对应角相等
【点睛】
本题考查了作一个角等于已知角的作图依据,正确理解作图过程是解题的关键.
10.4
【解析】
【分析】
由图可知,DE与AC是对应边,则B点的对应点在DE上方两个,在DE下方两个共有4个满足要求的点,也就有四个全等三角形.
【详解】
解:根据题意,DE与AC是对应边,则B点的对应点在DE的上方有两个点,下方也有两个点.如图:
故答案为4.
【点睛】
本题考查三角形全等的判定方法关键在于作图寻找全等三角形,做图时要做到不重不漏.
11.O 任意长 O′ OC C CD D′
【解析】
【分析】
根据作一个角等于已知角的作图方法解答即可.
【详解】
①以O为圆心,任意长为半径画弧.分别交OA , OB于点C、D .
②画一条射线O′A′,以O′为圆心,OC长为半径画弧,交O′A′于点C′,
③以点C为圆心CD长为半径画弧,与第2步中所画的弧交于点D′.
④过点D′画射线O′B′,则∠A′O′B′=∠AOB.
故答案为:(1). O; (2). 任意长;(3). O′; (4). OC; (5). C ; (6). CD ;(7). D′
【点睛】
本题主要考查了作一个角等于已知角,是基本作图,需熟练掌握.
12.
【解析】
【分析】
利用作法得到△C'O'D'和△COD的三边对应相等,从而根据SSS可证明△C'O'D'≌△COD,然后根据全等三角形的性质得到∠A'0'B'=∠A0B.
【详解】
解:由作法得0D=0C=0D'=OC',CD=C'D',则根据“SSS”可判断△C'O'D≌△COD,所以∠A'0'B'=∠A0B.
故答案:SSS.
【点睛】
本题考查了作图-基本作图:熟练掌握基本作图(作一条线段等于已知线段;作一个角等于已知角;作已知线段的垂直平分线;作已知角的角平分线;过一点作已知直线的垂线).也考查了角平分线的性质定理的逆定理.
13.②④
【解析】
【分析】
根据三角形的三边关系定理,先看看能否组成三角形,再根据全等三角形的判定定理判断即可.
【详解】
解:①∵3+4<8,∴根据AB=3,BC=4,AB=8不能画出三角形,故本选项错误;
②根据∠A=60°,∠B=30°,AB=4,符合全等三角形的判定定理ASA,即能画出唯一三角形,故本选项正确;
③根据AB=5,BC=3,∠A=30°不能画出唯一三角形,故本选项错误;
④根据AB=3,BC=4,AC=5,符合全等三角形的判定定理SSS,即能画出唯一三角形,故本选项正确;
故答案为:②④.
【点睛】
本题考查了三角形的三边关系定理和全等三角形的判定定理,注意:全等三角形的判定定理有SAS,ASA,AAS,SSS.
14.①③④
【解析】
【分析】
根据全等三角形的判定方法进行分析,从而得到答案.
【详解】
解:①符合全等三角形的判定定理SAS,即能画出唯一三角形,正确; ②根据BC=4cm,AC=3cm,∠ABC=30°不能画出唯一三角形,如图所示△ABC和△BCD, 错误;
③符合全等三角形的判定定理HL,即能画出唯一三角形,正确; ④∵∠ABC为钝角,结合②可知,只能画出唯一三角形,正确. 故答案为:①③④.
【点睛】
本题考查的是全等三角形的判定方法;解答此题的关键是要掌握三角形全等判定的几种方法即可,结合已知逐个验证,要找准对应关系.
15.见解析
【解析】
【分析】
利用全等三角形的判定定理SSS、AAS、ASA、SAS之一来作,作线段B′C′=BC,分别以B′、C′为圆心,BA,CA为半径画弧,两弧交于点A′,连接A′B′,A′C′.(答案不唯一)
【详解】
解:选取AB、BC、AC作图,使其分别等于A′B′、B′C′、A′C′,
如图,即为所作三角形:
【点睛】
本题考查作图-复杂作图,全等三角形的判定等知识,解题的关键是熟练掌握基本知识,属于中考常考题型.
16.见解析
【解析】
【分析】
利用SSS定理,分别以C,D为圆心,以AB,CA长为半径作弧交于点E,连接CE,DE即可得到.
【详解】
解:如图,即为所求作的三角形.
(作法不唯一)
【点睛】
本题考查了全等三角形和作图,关键是掌握全等三角形的判定定理.
17.详见解析.
【解析】
试题分析:先作∠MAN=α,再在AM上取AB=c,再以B为顶点作∠ABC=β,两角的一边交于点C,△ABC就是所求三角形.
试题解析:如图,△ABC就是所求三角形.
考点:尺规作图
18.(1)BD,MN; (2)三边对应相等的两个三角形全等;全等三角形的对应角相等;(3)小明没有对已知中的边和角的位置关系分类讨论.
【解析】
【分析】
根据题意,按步骤解答即可.
【详解】
(1)BD,MN;
(2)三边对应相等的两个三角形全等;全等三角形的对应角相等;
(3)小明没有对已知中的边和角的位置关系分类讨论.
【点睛】
本题考查了作图-复杂作图:复杂作图是在五种基本作图的基础上进行作图,一般是结合了几何图形的性质和基本作图方法.解决此类题目的关键是熟悉基本几何图形的性质,结合几何图形的基本性质把复杂作图拆解成基本作图,逐步操作.
同课章节目录
- 第一章 整式的乘除
- 1 同底数幂的乘法
- 2 幂的乘方与积的乘方
- 3 同底数幂的除法
- 4 整式的乘法
- 5 平方差公式
- 6 完全平方公式
- 7 整式的除法
- 第二章 相交线与平行线
- 1 两条直线的位置关系
- 2 探索直线平行的条件
- 3 平行线的性质
- 4 用尺规作角
- 第三章 变量之间的关系
- 1 用表格表示的变量间关系
- 2 用关系式表示的变量间关系
- 3 用图象表示的变量间关系
- 第四章 三角形
- 1 认识三角形
- 2 图形的全等
- 3 探索三角形全等的条件
- 4 用尺规作三角形
- 5 利用三角形全等测距离
- 第五章 生活中的轴对称
- 1 轴对称现象
- 2 探索轴对称的性质
- 3 简单的轴对称图形
- 4 利用轴对称进行设计
- 第六章 概率初步
- 1 感受可能性
- 2 频率的稳定性
- 3 等可能事件的概率
