第五章 抛体运动第1节曲线运动(共47张PPT)
文档属性
| 名称 | 第五章 抛体运动第1节曲线运动(共47张PPT) |  | |
| 格式 | zip | ||
| 文件大小 | 1.0MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(2019) | ||
| 科目 | 物理 | ||
| 更新时间 | 2020-02-14 13:36:03 | ||
图片预览










文档简介
(共47张PPT)
第五章 曲线运动
第1节 曲线运动
复习提问:
1、什么是直线运动?
2、物体做直线运动的条件是什么?
轨迹是直线的运动
物体所受的合力与速度在同一直线上
一、曲线运动及其位移
1.曲线运动
定义:运动轨迹是曲线的运动(相对于某一参考系)
2.曲线运动的位移
(1)定义:
曲线运动的位移是由初位置指向末位置的有向线段
矢量
大小:
方向:
该有向线段的长度
初位置→末位置
(2)位移的表示:
物体做二维平面曲线运动时,为了便于研究,可建立平面直角坐标系,其位移可用它在坐标轴上的分量表示
X
y
O
A
α
L
XA
yA
说明:y轴正方向向下,这时处于
x轴下方点的纵坐标为正值
物体从O点沿曲线运动到A点:
位移大小为L,方向与x轴的夹角为α
说明:
物体做曲线运动时,物体相对起始点的位移方向不断变化,在表示物体的位移时,尽量用它的位移在坐标轴上的分量来表示,而位移分量可用该点的坐标表示
想一想:
物体做曲线运动时,路程有可能等于位移的大小吗?
曲线运动和直线运动相比,除了运动轨迹不同,还有什么不同的地方?
曲线运动的速度方向在不断变化
怎样确定曲线运动中任意时刻(或任意位置)的速度方向呢?
想一想:
火星由于惯性,以脱离砂轮时的速度沿切线方向飞出,切线方向即为火星飞出时的速度方向
水滴沿伞边缘的切线方向飞出
结论:
物体做曲线运动的速度方向是时刻改变的,质点在某一点(或某一时刻)速度方向沿着曲线这一点的切线方向。
A
B
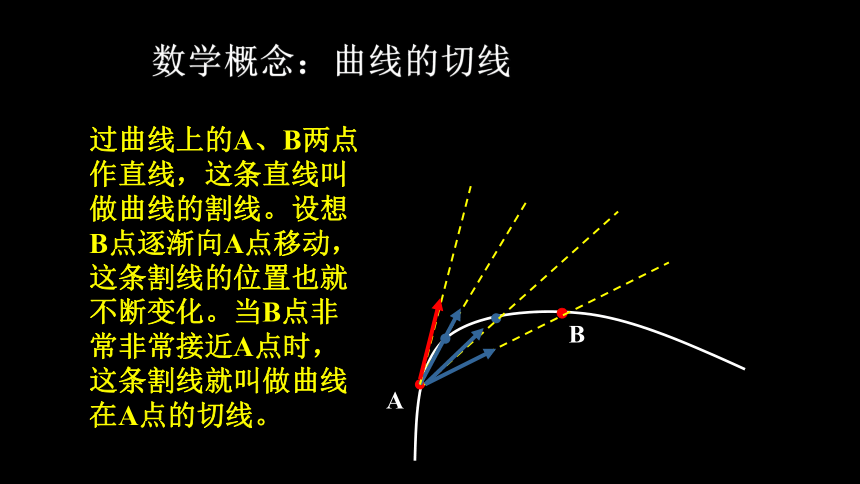
数学概念:曲线的切线
过曲线上的A、B两点作直线,这条直线叫做曲线的割线。设想B点逐渐向A点移动,这条割线的位置也就不断变化。当B点非常非常接近A点时,这条割线就叫做曲线在A点的切线。
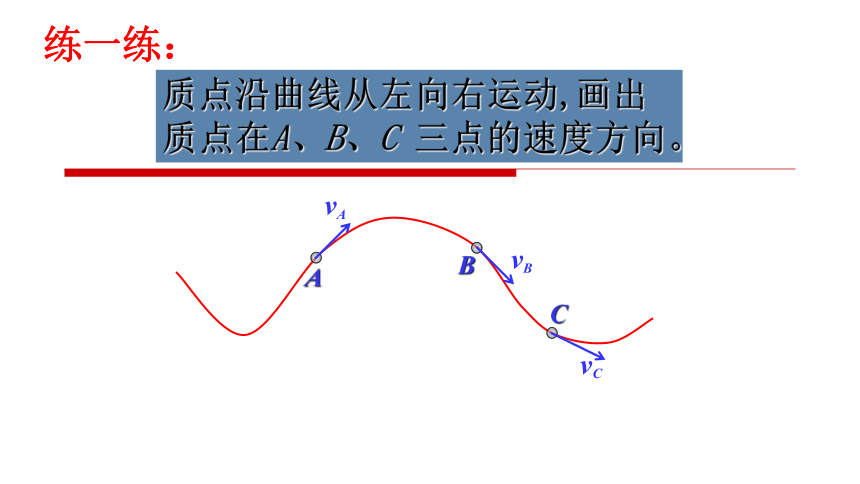
质点沿曲线从左向右运动,画出质点在A、B、C 三点的速度方向。
A
B
C
vA
vB
vC
练一练:
二、曲线运动的速度
1.曲线运动的速度方向及大小
(1)方向:
质点在某一点的速度方向,沿曲线在这一点的切线方向
(2)大小:
X
y
O
VX
Vy
v
θ
见鬼,被甩了一身泥……
生活实例:
请为自行车设计安装挡泥板
生活实例:
2.曲线运动的性质及分类
(1)性质:
变速运动
说明曲线运动一定有加速度,但不能确定加速度是否发生变化
(2)分类:
①匀变速曲线运动:
②非匀变速曲线运动:
加速度恒定
加速度变化
说明:
物体做曲线运动
速度方向一定发生变化
速度大小不一定发生变化
速度变化量不为0
一定有加速度
加速度可能恒定
合外力一定不为0
外力可能是恒力,也可能不是
外力一定不与速度共线
加速度一定不与速度共线
三、运动的合成与分解
1.蜡烛运动的研究
(1)蜡块的位置:
蜡块沿玻璃管匀速上升的速度设为Vy,玻璃管向右匀速移动的速度设为Vx,从蜡块开始运动的时刻计时:
在某时刻t,蜡块的位置R可以用它的x、y两个坐标表示:
x=vxt
y=vyt
(2)蜡块运动的轨迹:
x
y
y
O
θ
x
l
Vy
Vx
R
( x,y)
x=vxt
y=vyt
得:
蜡块的运动轨迹是一条过原点的直线
(3)蜡块的位移大小:
(4)蜡块的速度:
物体沿某一方向的速度
叫这一方向的分速度,
物体沿某一方向的位移
叫这一方向的分位移。
O
x
y
P
( x,y)
Vx
Vy
V
θ
S
x
y
物体的实际运动速度又叫合速度,
物体的实际运动位移又叫合位移。
2.运动的合成与分解
合运动与分运动
在物理学上,如果一个物体实际发生的运动产生的效果跟另外两个运动共同产生的效果相同,我们就把这一物体实际发生的运动叫做这两个运动的合运动,这两个运动叫做这一实际运动的分运动。
观察
用小锤打击弹性金属片C,观察到了什么?
现象:1.球A沿曲线飞行;球B沿直线运动。
2.不论初速度如何,二球总同时落地。
分析:
1.同一时间内,二球在竖直方向的距离总是相等(等时性) ;
2.球A 除竖直方向运动外,还有水平方向的运动,但水平方向运动对竖直方向运动无影响,反之亦然(独立性);
3.球A 运动正是水平方向和竖直方向运动的合运动,而水平方向和竖直方向运动分别是这一合运动的分运动(等效性) 。
结论:一个复杂的运动可看作几个独立分运动的合运动。
合运动与分运动的特点
(1)等时性
(2)等效性
O
x
y
P
( x,y)
Vx
Vy
V
θ
S
x
y
(5)矢量性:
合速度与分速度,合位移与分位移都遵循平行四边形定则。
(3)独立性
说一说
(4)同体性
注意:
运动合成与分解的原则
1.等效性原则
2.符合实际的原则
3.解题方便原则
注:运动的合成与分解互为逆运算
1、枪管与水平方向的夹角为600,子弹射出枪口时的速度为500m/s,则子弹沿水平方向的分速度的大小为 m/s,沿竖直方向的分速度的大小为 m/s。
Vx
Vy
V
600
Vx=Vcos600=250m/s
Vy=Vsin600=433m/s
例 题
2、飞机起飞时以V=100m/s的速度斜向上飞,飞行方向与水平面的夹角为370。求飞机在2s内飞行的高度。
Vy=Vsin370=60m/s
y=Vyt=120m
Vx
Vy
V
370
训 练
x
y
S
370
方法二:分解速度
方法一:分解位移
S=Vt=200m
y=Ssin370=120m
3、在高处拉低处小船时,通常在河岸上通过滑轮用钢绳拴船,若拉绳的速度为V1=4m/s,当拴船的绳与水平方向成60°时,船的速度是多大?
速度V1与 V哪一个是合速度?
V
V1
V2
V=V1/cos600=8m/s
提示:两个物体用绳或杆相连,则两物体沿绳或杆方向的分速度大小相等。
练 习
绳及杆的速度分解
θ
v1
v2
v
沿绳方向使绳伸长
垂直于绳方向使绳转动
绳(杆)模型绳(杆)端速度分解原则:
沿着绳(杆)和垂直绳(杆)
则V与V1的关系为 ?
注:绳(杆)两端速度大小一般不相等,但两端沿绳(杆)方向速度一定相等※
V1=VCOSθ
【例题】如图所示,以速度v沿竖直杆匀速下滑的物体A,用细绳通过定滑轮拉动物体B在水平桌面上运动,当绳与水平面夹角为θ时,物体B的速率为 。
【答案】 vB=vsinθ
寻找分运动效果
“绳+物”问题
【例题】如图所示,A、B两物体用细绳相连,在水平面上运动,当α=450,β=300时,物体A的速度为2 m/s,这时B的速度为 。
寻找分运动效果
【答案】
“绳+物”问题
【例题】如图所示,杆AB它的两端在地板和竖直墙壁上,现拉A端由图示位置以速率v匀速向右运动,B端滑动的速度是 。
寻找分运动效果
“杆+物”问题
α
Vcosθ
VBcosα
【例题】如图所示,滑块B以速度vB向左运动时,触点P的沿杆移动的速度如何?
【答案】
寻找分运动效果
“杆+物”问题
四、物体做曲线运动的条件
1.物体做曲线运动条件
(1)运动学条件:
物体加速度的方向与物体的速度方向不在同一条直线上
(2)动力学条件:
物体所受合力的方向与物体的速度方向不在同一条直线上
2.运动性质与速度和合力的夹角的关系
分类 速度和合力的夹角θ 运动性质 力的作用效果
直线运动 θ=00 加速直线运动 只改变速度的大小,不改变速度的方向
θ=1800 减速直线运动
曲线运动 00<θ<900 加速曲线运动 既改变速度的大小,又改变速度的方向
900<θ<1800 减速曲线运动
θ=900 速度大小不变的曲线运动 只改变速度的方向,不改变速度的大小
G
G
G
G
G
V1
V2
V3
V4
V
F
(1)合外力方向指向轨迹曲线的内侧(凹侧)!
(2)物体的轨迹位于速度和合外力之间。
3.曲线运动的特点
(3)X位(4)切向分力改变速度大小,法向分力改变速度方向
A
B
C
vA
vB
vC
说明:
F1
F2
F3
切向:
法向:
切线的方向
与切线垂直的方向
课堂练习
小球在水平桌面上做匀速直线运动,当它受到如图所示方向的力的作用时,小球可能运动的方向是( )
A、 Oa
B、 Ob
C、 Oc
D、 Od
D
如图所示,物体在恒力的作用下沿从A曲线运动到B,此时突然使力反向,物体 的运动情况是 ( )
A 物体可能沿曲线Ba运动
B 物体可能沿直线Bb运动
C 物体可能沿曲线Bc运动
D 物体可能沿曲线B返回A
C
课堂练习
F合(a)与v共线
直线运动
a恒定
a变化
匀变速直线运动
变加速直线运动
F合(a)与v不共线
曲线运动
a恒定
a变化
匀变速曲线运动
变加速曲线运动
a=0
匀速直线运动
a≠0
能力提升1:
1.合运动性质的判断
2.两个互成角度的直线运动的合运动性质的判断
合运动的性质取决于两个分运动的合初速度和合加速度(合外力)的关系
匀速
v1
匀速
v2
v
a1=0
a2=0
a=0
匀速
v1
匀加速
v2
v
a1=0
a2
(a)
v1=0匀加速
a
a1
a2
v=0
v2=0匀加速
匀速
v=0匀加速
v1
v2
v
a2
a1
a
匀加速
匀加速
匀加速
a2
a1
a
曲线
曲线
(1)讨论α=?时渡河时间最短。
d
V船
河宽d,静水中船速为V船,水流速度为V水,V船与河岸的夹角为α,如图所示。求:
(2)讨论α=?时,船的位移最短?
α
能力提升2:小船渡河问题
d
v水
v
v船
(一)渡河时间最短:
说明:当船头垂直对岸行驶时,渡河时间最短,且最短时间为:
渡河时间取决于V船与河水的速度无关。
位移:
时间:
合速度:
θ
分析:船在动水中渡河时的位移大小和方向,取决于船速和水速的合速度方向。
d
v船
渡河位移最短
v合
方向:
时间:
位移:
v水
⑴ v船>v水时:
当v合垂直河岸,合位移最短等于河宽d。
d
v水
smin
D
O
A
v船
θ
E
C
θ
θ
v
v船
B
上游
下游
渡河位移最短
(2)v船<v水时,当v船垂直于v合时,合位移最短,即:
结论:
船头垂直对岸行驶时,渡河时间最短
V船>V水,船能垂直过河,位移最短
V船练习:
1、 一船在静水中的速度为3m/s,要渡过宽为30m,流速为4m/s的河流,下列说法中不正确的是( )
A:此船能垂直到达河对岸
B:此船不可能垂直到达河对岸
C:此船对河岸速度一定为5m/s
D:过河时间可能为15s
A C
总结:
曲线运动
匀变速曲线运动
变加速曲线运动
①物体所受合外力方向与初速度的方向不在同一直线上
②合外力是恒力
①物体所受合外力方向与初速度的方向不在同一直线上
②合外力是变力(可以是力的大小改变,也可是力的方向改变或者二者同时改变)
例:平抛运动
例:人造地球卫星的运动
第五章 曲线运动
第1节 曲线运动
复习提问:
1、什么是直线运动?
2、物体做直线运动的条件是什么?
轨迹是直线的运动
物体所受的合力与速度在同一直线上
一、曲线运动及其位移
1.曲线运动
定义:运动轨迹是曲线的运动(相对于某一参考系)
2.曲线运动的位移
(1)定义:
曲线运动的位移是由初位置指向末位置的有向线段
矢量
大小:
方向:
该有向线段的长度
初位置→末位置
(2)位移的表示:
物体做二维平面曲线运动时,为了便于研究,可建立平面直角坐标系,其位移可用它在坐标轴上的分量表示
X
y
O
A
α
L
XA
yA
说明:y轴正方向向下,这时处于
x轴下方点的纵坐标为正值
物体从O点沿曲线运动到A点:
位移大小为L,方向与x轴的夹角为α
说明:
物体做曲线运动时,物体相对起始点的位移方向不断变化,在表示物体的位移时,尽量用它的位移在坐标轴上的分量来表示,而位移分量可用该点的坐标表示
想一想:
物体做曲线运动时,路程有可能等于位移的大小吗?
曲线运动和直线运动相比,除了运动轨迹不同,还有什么不同的地方?
曲线运动的速度方向在不断变化
怎样确定曲线运动中任意时刻(或任意位置)的速度方向呢?
想一想:
火星由于惯性,以脱离砂轮时的速度沿切线方向飞出,切线方向即为火星飞出时的速度方向
水滴沿伞边缘的切线方向飞出
结论:
物体做曲线运动的速度方向是时刻改变的,质点在某一点(或某一时刻)速度方向沿着曲线这一点的切线方向。
A
B
数学概念:曲线的切线
过曲线上的A、B两点作直线,这条直线叫做曲线的割线。设想B点逐渐向A点移动,这条割线的位置也就不断变化。当B点非常非常接近A点时,这条割线就叫做曲线在A点的切线。
质点沿曲线从左向右运动,画出质点在A、B、C 三点的速度方向。
A
B
C
vA
vB
vC
练一练:
二、曲线运动的速度
1.曲线运动的速度方向及大小
(1)方向:
质点在某一点的速度方向,沿曲线在这一点的切线方向
(2)大小:
X
y
O
VX
Vy
v
θ
见鬼,被甩了一身泥……
生活实例:
请为自行车设计安装挡泥板
生活实例:
2.曲线运动的性质及分类
(1)性质:
变速运动
说明曲线运动一定有加速度,但不能确定加速度是否发生变化
(2)分类:
①匀变速曲线运动:
②非匀变速曲线运动:
加速度恒定
加速度变化
说明:
物体做曲线运动
速度方向一定发生变化
速度大小不一定发生变化
速度变化量不为0
一定有加速度
加速度可能恒定
合外力一定不为0
外力可能是恒力,也可能不是
外力一定不与速度共线
加速度一定不与速度共线
三、运动的合成与分解
1.蜡烛运动的研究
(1)蜡块的位置:
蜡块沿玻璃管匀速上升的速度设为Vy,玻璃管向右匀速移动的速度设为Vx,从蜡块开始运动的时刻计时:
在某时刻t,蜡块的位置R可以用它的x、y两个坐标表示:
x=vxt
y=vyt
(2)蜡块运动的轨迹:
x
y
y
O
θ
x
l
Vy
Vx
R
( x,y)
x=vxt
y=vyt
得:
蜡块的运动轨迹是一条过原点的直线
(3)蜡块的位移大小:
(4)蜡块的速度:
物体沿某一方向的速度
叫这一方向的分速度,
物体沿某一方向的位移
叫这一方向的分位移。
O
x
y
P
( x,y)
Vx
Vy
V
θ
S
x
y
物体的实际运动速度又叫合速度,
物体的实际运动位移又叫合位移。
2.运动的合成与分解
合运动与分运动
在物理学上,如果一个物体实际发生的运动产生的效果跟另外两个运动共同产生的效果相同,我们就把这一物体实际发生的运动叫做这两个运动的合运动,这两个运动叫做这一实际运动的分运动。
观察
用小锤打击弹性金属片C,观察到了什么?
现象:1.球A沿曲线飞行;球B沿直线运动。
2.不论初速度如何,二球总同时落地。
分析:
1.同一时间内,二球在竖直方向的距离总是相等(等时性) ;
2.球A 除竖直方向运动外,还有水平方向的运动,但水平方向运动对竖直方向运动无影响,反之亦然(独立性);
3.球A 运动正是水平方向和竖直方向运动的合运动,而水平方向和竖直方向运动分别是这一合运动的分运动(等效性) 。
结论:一个复杂的运动可看作几个独立分运动的合运动。
合运动与分运动的特点
(1)等时性
(2)等效性
O
x
y
P
( x,y)
Vx
Vy
V
θ
S
x
y
(5)矢量性:
合速度与分速度,合位移与分位移都遵循平行四边形定则。
(3)独立性
说一说
(4)同体性
注意:
运动合成与分解的原则
1.等效性原则
2.符合实际的原则
3.解题方便原则
注:运动的合成与分解互为逆运算
1、枪管与水平方向的夹角为600,子弹射出枪口时的速度为500m/s,则子弹沿水平方向的分速度的大小为 m/s,沿竖直方向的分速度的大小为 m/s。
Vx
Vy
V
600
Vx=Vcos600=250m/s
Vy=Vsin600=433m/s
例 题
2、飞机起飞时以V=100m/s的速度斜向上飞,飞行方向与水平面的夹角为370。求飞机在2s内飞行的高度。
Vy=Vsin370=60m/s
y=Vyt=120m
Vx
Vy
V
370
训 练
x
y
S
370
方法二:分解速度
方法一:分解位移
S=Vt=200m
y=Ssin370=120m
3、在高处拉低处小船时,通常在河岸上通过滑轮用钢绳拴船,若拉绳的速度为V1=4m/s,当拴船的绳与水平方向成60°时,船的速度是多大?
速度V1与 V哪一个是合速度?
V
V1
V2
V=V1/cos600=8m/s
提示:两个物体用绳或杆相连,则两物体沿绳或杆方向的分速度大小相等。
练 习
绳及杆的速度分解
θ
v1
v2
v
沿绳方向使绳伸长
垂直于绳方向使绳转动
绳(杆)模型绳(杆)端速度分解原则:
沿着绳(杆)和垂直绳(杆)
则V与V1的关系为 ?
注:绳(杆)两端速度大小一般不相等,但两端沿绳(杆)方向速度一定相等※
V1=VCOSθ
【例题】如图所示,以速度v沿竖直杆匀速下滑的物体A,用细绳通过定滑轮拉动物体B在水平桌面上运动,当绳与水平面夹角为θ时,物体B的速率为 。
【答案】 vB=vsinθ
寻找分运动效果
“绳+物”问题
【例题】如图所示,A、B两物体用细绳相连,在水平面上运动,当α=450,β=300时,物体A的速度为2 m/s,这时B的速度为 。
寻找分运动效果
【答案】
“绳+物”问题
【例题】如图所示,杆AB它的两端在地板和竖直墙壁上,现拉A端由图示位置以速率v匀速向右运动,B端滑动的速度是 。
寻找分运动效果
“杆+物”问题
α
Vcosθ
VBcosα
【例题】如图所示,滑块B以速度vB向左运动时,触点P的沿杆移动的速度如何?
【答案】
寻找分运动效果
“杆+物”问题
四、物体做曲线运动的条件
1.物体做曲线运动条件
(1)运动学条件:
物体加速度的方向与物体的速度方向不在同一条直线上
(2)动力学条件:
物体所受合力的方向与物体的速度方向不在同一条直线上
2.运动性质与速度和合力的夹角的关系
分类 速度和合力的夹角θ 运动性质 力的作用效果
直线运动 θ=00 加速直线运动 只改变速度的大小,不改变速度的方向
θ=1800 减速直线运动
曲线运动 00<θ<900 加速曲线运动 既改变速度的大小,又改变速度的方向
900<θ<1800 减速曲线运动
θ=900 速度大小不变的曲线运动 只改变速度的方向,不改变速度的大小
G
G
G
G
G
V1
V2
V3
V4
V
F
(1)合外力方向指向轨迹曲线的内侧(凹侧)!
(2)物体的轨迹位于速度和合外力之间。
3.曲线运动的特点
(3)X位
A
B
C
vA
vB
vC
说明:
F1
F2
F3
切向:
法向:
切线的方向
与切线垂直的方向
课堂练习
小球在水平桌面上做匀速直线运动,当它受到如图所示方向的力的作用时,小球可能运动的方向是( )
A、 Oa
B、 Ob
C、 Oc
D、 Od
D
如图所示,物体在恒力的作用下沿从A曲线运动到B,此时突然使力反向,物体 的运动情况是 ( )
A 物体可能沿曲线Ba运动
B 物体可能沿直线Bb运动
C 物体可能沿曲线Bc运动
D 物体可能沿曲线B返回A
C
课堂练习
F合(a)与v共线
直线运动
a恒定
a变化
匀变速直线运动
变加速直线运动
F合(a)与v不共线
曲线运动
a恒定
a变化
匀变速曲线运动
变加速曲线运动
a=0
匀速直线运动
a≠0
能力提升1:
1.合运动性质的判断
2.两个互成角度的直线运动的合运动性质的判断
合运动的性质取决于两个分运动的合初速度和合加速度(合外力)的关系
匀速
v1
匀速
v2
v
a1=0
a2=0
a=0
匀速
v1
匀加速
v2
v
a1=0
a2
(a)
v1=0匀加速
a
a1
a2
v=0
v2=0匀加速
匀速
v=0匀加速
v1
v2
v
a2
a1
a
匀加速
匀加速
匀加速
a2
a1
a
曲线
曲线
(1)讨论α=?时渡河时间最短。
d
V船
河宽d,静水中船速为V船,水流速度为V水,V船与河岸的夹角为α,如图所示。求:
(2)讨论α=?时,船的位移最短?
α
能力提升2:小船渡河问题
d
v水
v
v船
(一)渡河时间最短:
说明:当船头垂直对岸行驶时,渡河时间最短,且最短时间为:
渡河时间取决于V船与河水的速度无关。
位移:
时间:
合速度:
θ
分析:船在动水中渡河时的位移大小和方向,取决于船速和水速的合速度方向。
d
v船
渡河位移最短
v合
方向:
时间:
位移:
v水
⑴ v船>v水时:
当v合垂直河岸,合位移最短等于河宽d。
d
v水
smin
D
O
A
v船
θ
E
C
θ
θ
v
v船
B
上游
下游
渡河位移最短
(2)v船<v水时,当v船垂直于v合时,合位移最短,即:
结论:
船头垂直对岸行驶时,渡河时间最短
V船>V水,船能垂直过河,位移最短
V船
1、 一船在静水中的速度为3m/s,要渡过宽为30m,流速为4m/s的河流,下列说法中不正确的是( )
A:此船能垂直到达河对岸
B:此船不可能垂直到达河对岸
C:此船对河岸速度一定为5m/s
D:过河时间可能为15s
A C
总结:
曲线运动
匀变速曲线运动
变加速曲线运动
①物体所受合外力方向与初速度的方向不在同一直线上
②合外力是恒力
①物体所受合外力方向与初速度的方向不在同一直线上
②合外力是变力(可以是力的大小改变,也可是力的方向改变或者二者同时改变)
例:平抛运动
例:人造地球卫星的运动
