鲁教版六年级下册数学5.4角的比较学案(习题不含答案)
文档属性
| 名称 | 鲁教版六年级下册数学5.4角的比较学案(习题不含答案) |
|
|
| 格式 | zip | ||
| 文件大小 | 118.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 鲁教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-02-14 00:00:00 | ||
图片预览

文档简介
5.4角的比较
学习目标
1、经历比较角的大小的研究过程,体会角的比较和线段的比较方法的一致性;
2、会比较角的大小,能估计一个角的大小;
3、在操作活动中认识角的平分线,能画出一个角的平分线.
学习重难点
重点:会比较角的大小,并会利用角的平分线解决问题
难题:理解角的比较和角平分线
学习过程
回顾旧知,目标定向
思考我们是如何比较线段的长短的?比较线段AB、CD的长度。
比较线段长短的方法_______________、__________________
迁移运用,探究新知
类比线段的比较方法,猜想如何比较角的大小:_______________、_______________
度量法:用_______________测量角的度数,并比较大小。
叠合法:(1)将两个角的________及_________重合
两个角的________落在重合一边的__________
由两个角的另一边的位置确定两个角的大小
比较下列∠ABC和∠DEF的大小:
______________ ______________ ______________
角的和差:
和:∠_______+∠_______=∠AOC 差:∠________—∠________=∠AOC
5、针对练习:
合作学习,交流展示
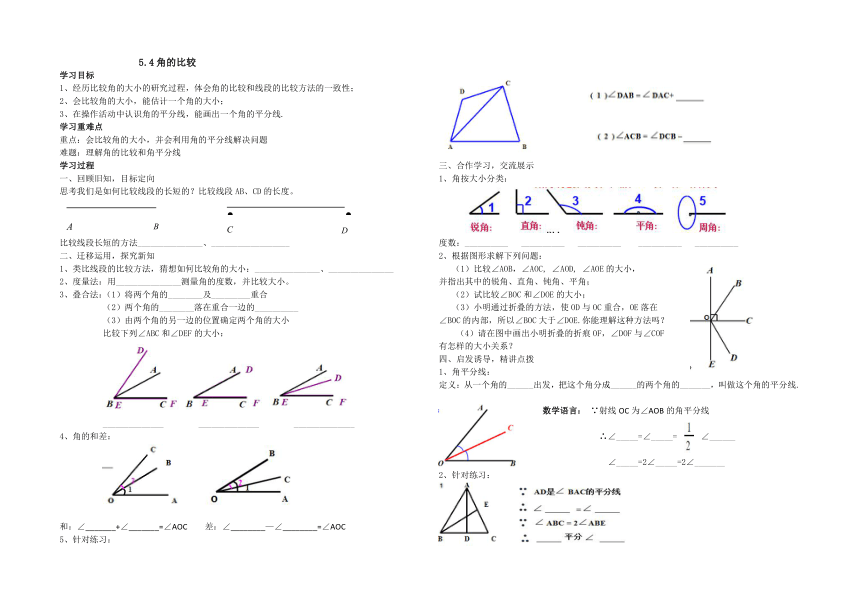
1、角按大小分类:
度数:__________ __________ __________ __________ __________
2、根据图形求解下列问题:
(1)比较∠AOB,∠AOC, ∠AOD, ∠AOE的大小,
并指出其中的锐角、直角、钝角、平角;
(2)试比较∠BOC和∠DOE的大小;
(3)小明通过折叠的方法,使OD与OC重合,OE落在
∠BOC的内部,所以∠BOC大于∠DOE.你能理解这种方法吗?
(4)请在图中画出小明折叠的折痕OF,∠DOF与∠COF
有怎样的大小关系?
启发诱导,精讲点拨
1、角平分线:
定义:从一个角的______出发,把这个角分成______的两个角的_______,叫做这个角的平分线.
数学语言: ∵射线OC为∠AOB的角平分线
∴∠_____=∠_____= ∠______
∠_____=2∠_____=2∠_______
针对练习:
系列训练,当堂达标
1、根据图形填空:
①∠DBA=∠DBC+ ;[来源:学_科_网]
②∠DBC=∠DBP- =∠DBA- ;
2、变式训练 (同图一)
(1)如图若∠ABC=90?,∠CBD=30?,你能求出哪些角的度数?
(2)若在(1)的条件下再添上条件BP平分∠ABD,你还能求出哪些角的度数?
3、射线OC在∠AOB内部,下列给出的条件中不能得到OC为∠AOB的平分线的是( )
A、2∠AOC=∠BOA B、∠AOB=2∠BOC
C、∠AOC+∠BOC=∠AOB D、∠AOC=∠BOC
4、如图1-33,若∠AOB=∠COB=∠DOC,进行下列填空。
(1)∠AOD=(? )+(? )+(? );
(2)∠AOB=(? )∠AOD;
(3)∠AOD=(? )∠COB;
(4)∠DOB=(? )=(? )+(? )。
拓展:
已知∠AOB=145°和∠AOC=25°, 则∠BOC=?
提示:先画图,图形就一种情况吗?
实践活动:
用一副三角板能画出那些度数的角?
回扣目标,总结反思
角的比较方法
角的和差
角平分线
思想方法
.
.
A
B
C
D
?
?
P
A
C
B
D
学习目标
1、经历比较角的大小的研究过程,体会角的比较和线段的比较方法的一致性;
2、会比较角的大小,能估计一个角的大小;
3、在操作活动中认识角的平分线,能画出一个角的平分线.
学习重难点
重点:会比较角的大小,并会利用角的平分线解决问题
难题:理解角的比较和角平分线
学习过程
回顾旧知,目标定向
思考我们是如何比较线段的长短的?比较线段AB、CD的长度。
比较线段长短的方法_______________、__________________
迁移运用,探究新知
类比线段的比较方法,猜想如何比较角的大小:_______________、_______________
度量法:用_______________测量角的度数,并比较大小。
叠合法:(1)将两个角的________及_________重合
两个角的________落在重合一边的__________
由两个角的另一边的位置确定两个角的大小
比较下列∠ABC和∠DEF的大小:
______________ ______________ ______________
角的和差:
和:∠_______+∠_______=∠AOC 差:∠________—∠________=∠AOC
5、针对练习:
合作学习,交流展示
1、角按大小分类:
度数:__________ __________ __________ __________ __________
2、根据图形求解下列问题:
(1)比较∠AOB,∠AOC, ∠AOD, ∠AOE的大小,
并指出其中的锐角、直角、钝角、平角;
(2)试比较∠BOC和∠DOE的大小;
(3)小明通过折叠的方法,使OD与OC重合,OE落在
∠BOC的内部,所以∠BOC大于∠DOE.你能理解这种方法吗?
(4)请在图中画出小明折叠的折痕OF,∠DOF与∠COF
有怎样的大小关系?
启发诱导,精讲点拨
1、角平分线:
定义:从一个角的______出发,把这个角分成______的两个角的_______,叫做这个角的平分线.
数学语言: ∵射线OC为∠AOB的角平分线
∴∠_____=∠_____= ∠______
∠_____=2∠_____=2∠_______
针对练习:
系列训练,当堂达标
1、根据图形填空:
①∠DBA=∠DBC+ ;[来源:学_科_网]
②∠DBC=∠DBP- =∠DBA- ;
2、变式训练 (同图一)
(1)如图若∠ABC=90?,∠CBD=30?,你能求出哪些角的度数?
(2)若在(1)的条件下再添上条件BP平分∠ABD,你还能求出哪些角的度数?
3、射线OC在∠AOB内部,下列给出的条件中不能得到OC为∠AOB的平分线的是( )
A、2∠AOC=∠BOA B、∠AOB=2∠BOC
C、∠AOC+∠BOC=∠AOB D、∠AOC=∠BOC
4、如图1-33,若∠AOB=∠COB=∠DOC,进行下列填空。
(1)∠AOD=(? )+(? )+(? );
(2)∠AOB=(? )∠AOD;
(3)∠AOD=(? )∠COB;
(4)∠DOB=(? )=(? )+(? )。
拓展:
已知∠AOB=145°和∠AOC=25°, 则∠BOC=?
提示:先画图,图形就一种情况吗?
实践活动:
用一副三角板能画出那些度数的角?
回扣目标,总结反思
角的比较方法
角的和差
角平分线
思想方法
.
.
A
B
C
D
?
?
P
A
C
B
D
同课章节目录
- 第五章 基本平面图形
- 1 线段、射线、 直线
- 2 比较线段的长短
- 3 角
- 4 角的比较
- 5 多边形和圆的初步认识
- 第六章 整式的乘除
- 1 同底数幂的乘法
- 2 幂的乘方与积的乘方
- 3 同底数幂的除法
- 4 零指数幂与负整数指数幂
- 5 整式的乘法
- 6 平方差公式
- 7 完全平方公式
- 8 整式的除法
- 第七章 相交线与平行线
- 1 两条直线的位置关系
- 2 探索直线平行的条件
- 3 平行线的性质
- 4 用尺规作角
- 第八章 数据的收集与整理
- 1 数据的收集
- 2 普查和抽样调查
- 3 数据的表示
- 4 统计图的选择
- 第九章 变量之间的关系
- 1 用表格表示变量之间的关系
- 2 用表达式表示变量之间的关系
- 3 用图象表示变量之间的关系
