湘教版九年级数学下册 1.4二次函数与一元二次方程的联系同步练习题(含答案)
文档属性
| 名称 | 湘教版九年级数学下册 1.4二次函数与一元二次方程的联系同步练习题(含答案) |  | |
| 格式 | zip | ||
| 文件大小 | 248.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 湘教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-02-14 11:41:30 | ||
图片预览

文档简介
1.4二次函数与一元二次方程的联系同步练习题
姓名:__________ 班级:__________考号:__________
一、单选题(共10题;共30分)
1.抛物线y=x2+2x+3与y轴的交点为(??? )
A.?(0,2)?????????????????????????????????B.?(2,0)?????????????????????????????????C.?(0,3)?????????????????????????????????D.?(3,0)
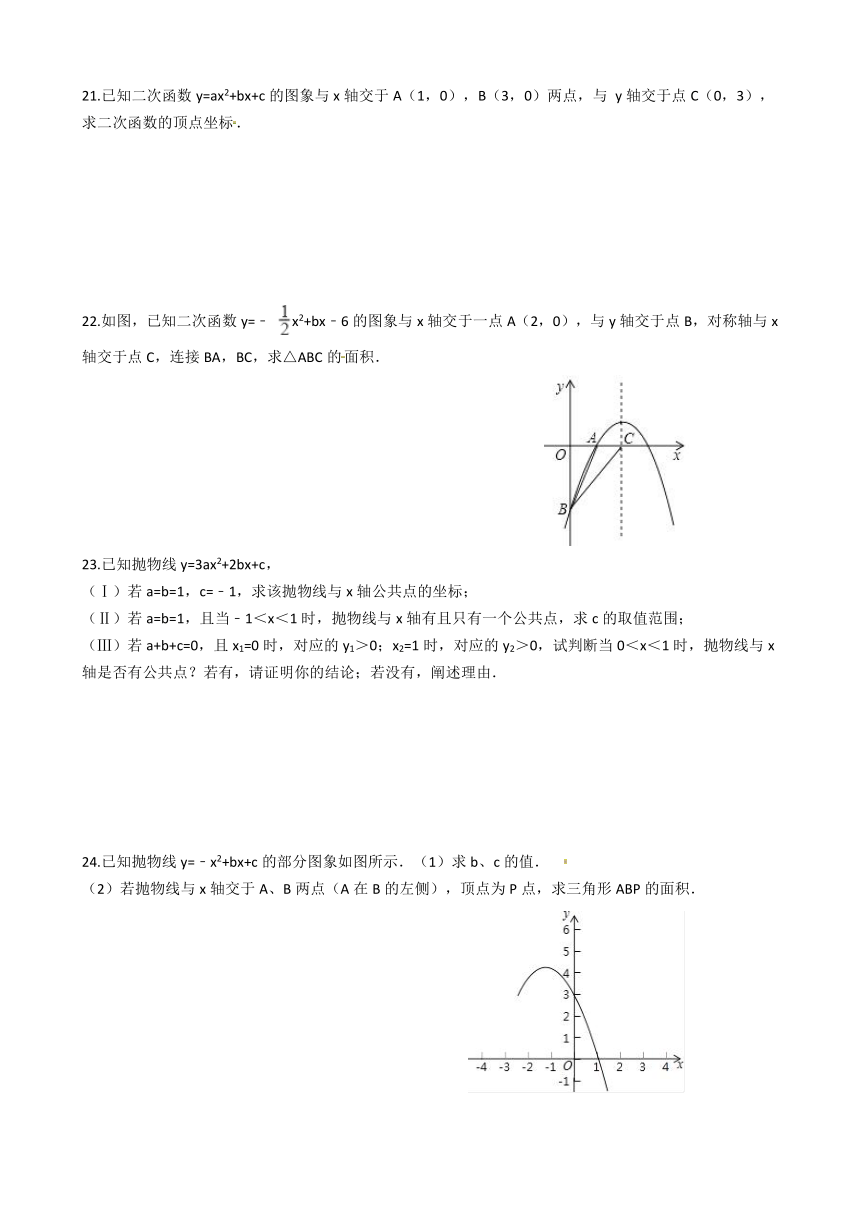
2.若关于x的方程x2﹣mx+n=0没有实数解,则抛物线y=x2﹣mx+n与x轴的交点有(?? )
A.?2个????????????????????????????????????B.?1个????????????????????????????????????C.?0个????????????????????????????????????D.?不能确定
3.不论x为何值,函数y=ax2+bx+c(a≠0)的值恒大于0的条件是(?? )
A.?a>0,△>0??????????????????????????B.?a>0, △<0??????????????????????????C.?a<0, △<0??????????????????????????D.?a<0, △<0
4.下列表格是二次函数y=ax2+bx+c(d≠0)的自变量x与函数y的一些对应值,由此可以判断方程ax2+bx+c=0(a≠0)的一个根在(?? )
x 6.17 6.18 6.19 6.20
y=ax2+bx+c ﹣0.03 ﹣0.01 0.02 0.06
A.?﹣0.01﹣0.02之间????????????B.?0.02﹣0.06之间????????????C.?6.17﹣6.18之间????????????D.?6.18﹣6.19之间
5.根据下表中的二次函数y=ax2+bx+c的自变量x与函数y的对应值,可判断该二次函数的图象与x轴( )
A.?只有一个交点 B.?有两个交点,且它们分别在y轴两侧
C.?有两个交点,且它们均在y轴同侧 D.?无交点
6.表是用计算器探索函数y=2x2﹣2x﹣10所得的数值,则方程2x2﹣2x﹣10=0的一个近似解为( )
????? x ??? ﹣2.1 ??? ﹣2.2 ?? ﹣2.3 ??? ﹣2.4
????? y ?? ﹣1.39 ??? ﹣0.76 ?? ﹣0.11 ???? 0.56
A.?x=﹣2.1??????????????????????????????B.?x=﹣2.2?????????????????????????????C.?x=﹣2.3?????????????????????????????D.?x=﹣2.4
7.若二次函数 y=ax2+bx+c(a<0) 的图象经过点(2,0),且其对称轴为直线 x=?1 ,则使函数值 y>0 成立的 x 的取值范围是(?? )
A.?x2??????????????B.??4 ≤ x ?≤ 2 C.?x ≤ ?4 或 x ≥ 2???????????D.??4
A.?-1<x<4?????????????????????B.?-1<x<3???????????????????
C.?x<-1或x>4??????????????????D.?x<-1或x>3
9.已知二次函数y=ax2﹣bx+0.5b﹣a与x轴交于A、B两点,则线段AB的最小值为(?? )
A.?0.5?????????????????????????????????????B.?2?????????????????????????????????????C.??????????????????????????????????????D.?无法确定
10.二次函数y=x2+x+c的图象与x轴的两个交点A(x1,0),B(x2,0),且x1<x2,点P(m,n)是图象上一点,那么下列判断正确的是( )
A.?当n<0时,m<0??????B.?当n>0时,m>x2??????C.?当n<0时,x1<m<x2??????D.?当n>0时,m<x1
二、填空题(共8题;共24分)
11.若函数 的图象与x轴只有一个公共点,则m=________.
12.抛物线y=ax2+bx+c的对称轴是x=2,其函数图象与x轴有两个交点,其中一个交点的坐标为(5,0),则另一个交点坐标为________.
13.在实验中我们常常采用利用计算机在平面直角坐标系中画出抛物线y=x2和直线y=﹣x+3,利用两图象交点的横坐标来求一元二次方程x2+x﹣3=0的解,也可以在平面直角坐标系中画出抛物线y=x2﹣3和直线y=﹣x,用它们交点的横坐标来求该方程的解.所以求方程的近似解也可以利用熟悉的函数________和________的图象交点的横坐标来求得.
14.若函数y=x2﹣3|x﹣1|﹣4x﹣3﹣b(b为常数)的图象与x轴恰好有三个交点,则常数b的值为________.
15.不等式x2+ax+b≥0(a≠0)的解集为全体实数,假设f(x)=x2+ax+b,若关于x的不等式f(x)<c的解集为(m,m+6),则实数c的值为________
16.如图,是二次函数y=ax2+bx﹣c的部分图象,由图象可知关于x的一元二次方程ax2+bx=c的两个根可能是________.(精确到0.1)
17.如图,抛物线y=ax2+bx+c(a>0)的对称轴是过点(1,0)且平行于y轴的直线,若点P(4,0)在该抛物线上,则4a﹣2b+c的值为________
18.如图,点A,B的坐标分别为(1,4)和(4,4),抛物线y=a(x+m)2+n的顶点在线段AB上,与x轴交于C,D两点(C在D的左侧),点C的横坐标最小值为﹣3,则点D的横坐标的最大值为________.
三、解答题(共8题;共66分)
19.结合二次函数的学习,求不等式x2+5x﹣6>0的解集.
20.二次函数y=x2﹣2x﹣3的图象与x轴交于A、B两点,与y轴交于点C,求S△ABC的面积.
21.已知二次函数y=ax2+bx+c的图象与x轴交于A(1,0),B(3,0)两点,与 y轴交于点C(0,3),求二次函数的顶点坐标.
22.如图,已知二次函数y=﹣ x2+bx﹣6的图象与x轴交于一点A(2,0),与y轴交于点B,对称轴与x轴交于点C,连接BA,BC,求△ABC的面积.
23.已知抛物线y=3ax2+2bx+c,
(Ⅰ)若a=b=1,c=﹣1,求该抛物线与x轴公共点的坐标;
(Ⅱ)若a=b=1,且当﹣1<x<1时,抛物线与x轴有且只有一个公共点,求c的取值范围;
(Ⅲ)若a+b+c=0,且x1=0时,对应的y1>0;x2=1时,对应的y2>0,试判断当0<x<1时,抛物线与x轴是否有公共点?若有,请证明你的结论;若没有,阐述理由.
24.已知抛物线y=﹣x2+bx+c的部分图象如图所示.(1)求b、c的值.
(2)若抛物线与x轴交于A、B两点(A在B的左侧),顶点为P点,求三角形ABP的面积.
25.如图,抛物线y=ax2+bx+c与x轴交于A(﹣1,0)和B(3,0)两点,交y轴于点E(0,﹣3).
(1)求此抛物线的解析式.
(2)若直线y=x+b与抛物线交于A、D两点,与y轴交于点F,连接DE,求△DEF的面积.
26.已知函数y=mx2+(2m+1)x+2(m为实数).
(1)请探究该函数图象与x轴的公共点个数的情况(要求说明理由);
(2)在图中给出的平面直角坐标系中分别画出m=﹣1和m=1的函数图象,并根据图象直接写出它们的交点坐标;(3)探究:对任意实数m,函数的图象是否一定过(2)中的点,并说明理由.
答案
一、单选题
1. C 2. C 3. B 4. D 5. B 6. C 7. D 8. B 9. C 10.C
二、填空题
11. 或0 12.(﹣1,0) 13. y=;y=x2﹣3 14. -6 15. 9 16. x1=0.8,x2=3.2合理即可
17. 0 18. 8
三、解答题
19.解:设y=x2+5x﹣6,函数图象如图所示:
由函数图象可知不等式x2+5x﹣6>0的解集为x>1或x<﹣6。
20.解:当y=0时,x2﹣2x﹣3=0, ∴(x+1)(x﹣3)=0,
解得:x1=﹣1,x2=3,∴AB=3﹣(﹣1)=4,
当x=0时,y=﹣3,∴CO=3,∴S△ABC= ×3×4=6.
21.解:把A(1,0),B(3,0),C(0,3)代入y=ax2+bx+c中得:
, 解得: ,
∴二次函数的解析式为:y=x2﹣4x+3,
y=x2﹣4x+3=(x﹣2)2﹣1,顶点坐标为(2,﹣1)
22.解:将A(2,0)代入函数y=﹣ x2+bx﹣6,
得:0=﹣2+2b﹣6,解得:b=4,
∴二次函数解析式为y=﹣ x2+4x﹣6.
当x=0时,y=﹣6,∴B(0,﹣6),
抛物线对称轴为x=﹣ =4,∴C(4,0),∴S△ABC= AC?OB= ×(4﹣2)×6=6
23.解:(Ⅰ)当a=b=1,c=﹣1时,抛物线为y=3x2+2x﹣1,
方程3x2+2x﹣1=0的两个根为x1=﹣1, .
∴该抛物线与x轴公共点的坐标是(﹣1,0)和( ,0);
(Ⅱ)当a=b=1时,抛物线为y=3x2+2x+c,且与x轴有公共点.
对于方程3x2+2x+c=0,判别式△=4﹣12c≥0,有c≤ .
①当 时,由方程3x2+2x+ =0,解得x1=x2=﹣ .
此时抛物线为y=3x2+2x+ 与x轴只有一个公共点(﹣ ,0);
②当 时,x1=﹣1时,y1=3﹣2+c=1+c;x2=1时,y2=3+2+c=5+c.
由已知﹣1<x<1时,该抛物线与x轴有且只有一个公共点,考虑其对称轴为 ,
应有 即 ,解得﹣5<c≤﹣1.综上, 或﹣5<c≤﹣1.(6分)
(Ⅲ)对于二次函数y=3ax2+2bx+c,
由已知x1=0时,y1=c>0;x2=1时,y2=3a+2b+c>0,
又∵a+b+c=0,∴3a+2b+c=(a+b+c)+2a+b=2a+b.∴2a+b>0.
∵b=﹣a﹣c,∴2a﹣a﹣c>0,即a﹣c>0.∴a>c>0.(7分)
∵关于x的一元二次方程3ax2+2bx+c=0的判别式△=4b2﹣12ac=4(a+c)2﹣12ac=4[(a﹣c)2+ac]>0,
∴抛物线y=3ax2+2bx+c与x轴有两个公共点,顶点在x轴下方.
又该抛物线的对称轴 ,由a+b+c=0,c>0,2a+b>0,得﹣2a<b<﹣a,
∴ .
又由已知x1=0时,y1>0;x2=1时,y2>0,观察图象,
可知在0<x<1范围内,该抛物线与x轴有两个公共点.
24.(1)解:观察函数图象可知:点(0,3)、(1,0)在抛物线上,
将点(0,3)、(1,0)代入y=﹣x2+bx+c中,
得: ,解得: ,∴b的值为﹣2,c的值为3.
(2)解:由(1)可知,抛物线的解析式为y=﹣x2﹣2x+3=﹣(x+1)2+4,
∴抛物线的顶点P的坐标为(﹣1,4).
令y=0,则有﹣x2﹣2x+3=0,解得:x1=﹣3,x2=1,
∵A在B的左侧,∴A(﹣3,0),B(1,0).
∴S△ABP= ?(x2﹣x1)?yp= ×[1﹣(﹣3)]×4=8.
25.(1)解:设抛物线解析式为y=a(x+1)(x﹣3),
把E(0,﹣3)代入得a?1?(﹣3)=﹣3,解得a=1,
所以抛物线解析式为y=(x+1)(x﹣3),即y=x2﹣2x﹣3
(2)解:把A(﹣1,0)代入y=x+b得﹣1+b=0,解得b=1,
∴直线AD的解析式为y=x+1,
当x=0时,y=x+1=1,则F(0,1),
解方程组 得 或 ,则D(4,5),
∴△DEF的面积= ×4×4=8
26.(1)解:当m=0时,y=x+2,此直线与x轴交于(﹣2,0);
当m≠0时,△=(2m+1)2﹣8m=(2m﹣1)2≥0,
∴此抛物线在m= 时,与x轴只有一个公共点;在m≠ 时,与x轴有2个交点
(2)解:当m=﹣1时,抛物线解析式为y=﹣x2﹣x+2,
当m=1时,抛物线解析式为y=x2+3x+2,
函数图象如下:
由函数图象知,两抛物线的交点为(﹣2,0)和(0,2)
(3)解:对任意实数m,函数的图象一定过(﹣2,0)和(0,2,理由如下:
在函数y=mx2+(2m+1)x+2中,
无论m为何值,当x=0时,y的值均为2,即横过点(0,2),
∵y=mx2+(2m+1)x+2=(x+2)(mx+1),
∴当x=﹣2时,y的值均为0,即函数图象横过(﹣2,0),
故无论m为何值,函数的图象(﹣2,0)和(0,2)两点
