青岛版七年级下册数学8.5垂直课件(22张PPT)
文档属性
| 名称 | 青岛版七年级下册数学8.5垂直课件(22张PPT) |
|
|
| 格式 | zip | ||
| 文件大小 | 697.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 青岛版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-02-14 00:00:00 | ||
图片预览







文档简介
(共22张PPT)
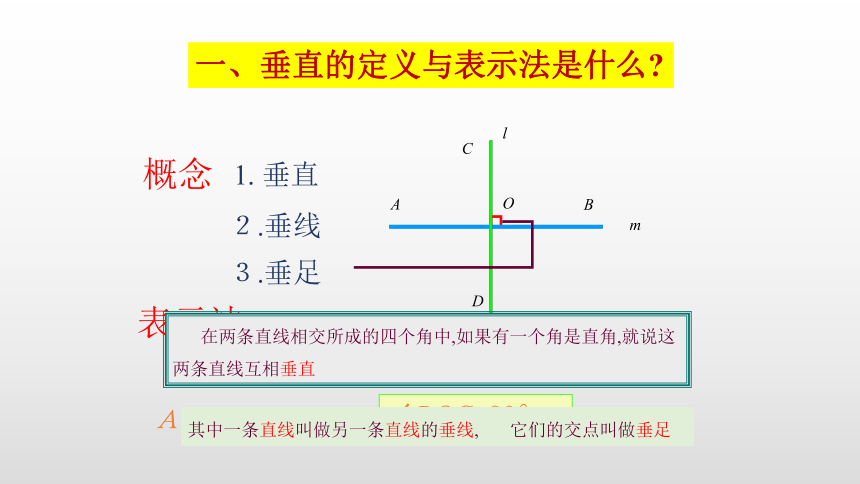
观察图形中的相交直线有何特点?
【学习目标】
1.能说出垂线的定义,会用符号表示两条直线互相垂直。
2.会画垂线,并在操作活动中探索、掌握垂线的性质。
3.从生活实际中感知“垂线段最短”,并能运用解决实际问题。
自主学习+小组交流
阅读课本P19--P21,思考下列问题
垂直的定义与表示法是什么?
怎样画垂线?
垂线的性质是什么?
什么是点到直线的距离?
A
D
C
l
m
O
B
概念
1. 垂直
2.垂线
3.垂足
表示法
AB⊥CD
m⊥l
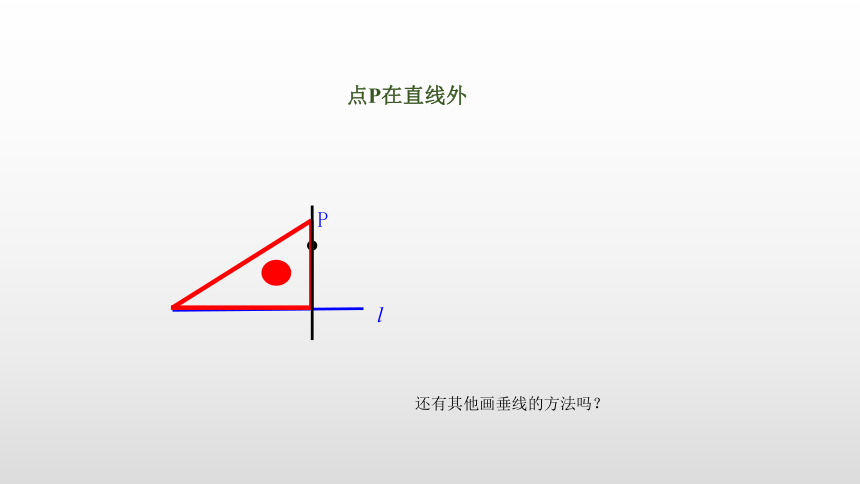
一、垂直的定义与表示法是什么?
∠BOC=90°
在两条直线相交所成的四个角中,如果有一个角是直角,就说这两条直线互相垂直
其中一条直线叫做另一条直线的垂线, 它们的交点叫做垂足
例:如图直线AB与直线CD相交于点O,OE⊥AB.
已知∠BOD=45°,求∠COE的度数.
解:
∵直线AB与直线CD相交于点O
∴∠AOC=∠BOD=45°(对顶角相等)
∵OE⊥AB
∴∠AOE=90°
∴∠COE=∠AOC+∠AOE
=45°+90°
=135°
(济南中考)已知:如图,AB⊥CD,垂足为O,EF为过点O的一条直线,则∠1与∠2的关系一定成立的是( )
A.相等 B.互余
C.互补 D.互为对顶角
B
解析:∵AB⊥CD,垂足为O
∴∠COB=90°
即∠COE+∠1=90°
∵EF为过点O的一条直线
∴∠COE=∠2 (对顶角相等)
∴∠2+∠1=90°(等量代换)
∴∠2与∠1互余
二、画垂线的方法
画垂线的方法可归纳为“一落、二过、三画”
3.三画:沿着直角边经过已知点画直线。
1.一落:把三角尺的一条直角边落在已知直线上;
2.二过:让三角尺的另一条直角边经过已知的点
若点P在直线外?
l
P
点P在直线外
还有其他画垂线的方法吗?
如何画一条线段或一条射线的垂线?
画已知线段、射线的垂线其实就是经过已知点作已知线段、射线所在的直线的垂线.
1、过点 向线段 所在直线引垂线,正确的是( ).
C
三、垂线的性质
1、下列说法中,不正确的是( )
A.一条直线的垂线有无数条;
B.过一点画直线的垂线,垂足必在直线上;
C.过射线外一点可以画这条射线的一条垂线
D.如果两条直线不相交,那么这两条直线有可能互相垂直
D
过直线外一点向已知直线作垂线时,这一点与垂足之间的线段叫做已知直线的垂线段.
P
O
线段PO是点P到直线m的垂线段
m
垂线段AD的长度叫做点A到直线l的距离
如图,在线段AB、AC、AD、AE中,哪条线段最短?得到什么结论?
1.点到直线的距离是指( )
A.直线外一点到这条直线的垂线段
B.直线外一点到这条直线的垂线段的长度
C.直线外一点到这条直线的垂线的长度
D.直线外一点到这条线上任意一点的距离
B
2、如图,在灌溉时需要把河AB中的水引到C处,如何挖渠能使渠道最短?
A
B
C
D
垂直的定义与表示法
垂线的画法
垂线的性质
点到直线的距离
垂直
1.(西安·中考)如图,点O在直线AB
上,且OC⊥OD,若∠COA=36°,则
∠DOB的大小为( )
A.36° B.54° C.64° D.72°
【解析】选B.因为OC⊥OD,所以∠COD=90°,又因为∠AOB=180°,所以∠DOB=∠AOB-∠COD-∠COA=180°-90°-36°=54°.
2.如图,OD⊥BC,D是垂足,连接OB,有下列说法:
①线段OB是O,B两点的距离
②线段OB的长度是O,B两点的距离
③线段OD是O点到直线BC的距离
④线段OD的长度是O点到直线BC的距离
其中正确的说法有( )个
A.1 B.2 C.3 D.4
O
B
D
C
B
3.如图所示,AC=4,BC=3,AB=5,则点C到
直线AB的距离是 .
【解析】作CD⊥AB,垂足为点D,则CD的长度就是点C到直线AB的距离,三角形ABC的面积为
,即 ,
所以CD=2.4.
【答案】2.4
Best Wish For You
信心源自于努力
观察图形中的相交直线有何特点?
【学习目标】
1.能说出垂线的定义,会用符号表示两条直线互相垂直。
2.会画垂线,并在操作活动中探索、掌握垂线的性质。
3.从生活实际中感知“垂线段最短”,并能运用解决实际问题。
自主学习+小组交流
阅读课本P19--P21,思考下列问题
垂直的定义与表示法是什么?
怎样画垂线?
垂线的性质是什么?
什么是点到直线的距离?
A
D
C
l
m
O
B
概念
1. 垂直
2.垂线
3.垂足
表示法
AB⊥CD
m⊥l
一、垂直的定义与表示法是什么?
∠BOC=90°
在两条直线相交所成的四个角中,如果有一个角是直角,就说这两条直线互相垂直
其中一条直线叫做另一条直线的垂线, 它们的交点叫做垂足
例:如图直线AB与直线CD相交于点O,OE⊥AB.
已知∠BOD=45°,求∠COE的度数.
解:
∵直线AB与直线CD相交于点O
∴∠AOC=∠BOD=45°(对顶角相等)
∵OE⊥AB
∴∠AOE=90°
∴∠COE=∠AOC+∠AOE
=45°+90°
=135°
(济南中考)已知:如图,AB⊥CD,垂足为O,EF为过点O的一条直线,则∠1与∠2的关系一定成立的是( )
A.相等 B.互余
C.互补 D.互为对顶角
B
解析:∵AB⊥CD,垂足为O
∴∠COB=90°
即∠COE+∠1=90°
∵EF为过点O的一条直线
∴∠COE=∠2 (对顶角相等)
∴∠2+∠1=90°(等量代换)
∴∠2与∠1互余
二、画垂线的方法
画垂线的方法可归纳为“一落、二过、三画”
3.三画:沿着直角边经过已知点画直线。
1.一落:把三角尺的一条直角边落在已知直线上;
2.二过:让三角尺的另一条直角边经过已知的点
若点P在直线外?
l
P
点P在直线外
还有其他画垂线的方法吗?
如何画一条线段或一条射线的垂线?
画已知线段、射线的垂线其实就是经过已知点作已知线段、射线所在的直线的垂线.
1、过点 向线段 所在直线引垂线,正确的是( ).
C
三、垂线的性质
1、下列说法中,不正确的是( )
A.一条直线的垂线有无数条;
B.过一点画直线的垂线,垂足必在直线上;
C.过射线外一点可以画这条射线的一条垂线
D.如果两条直线不相交,那么这两条直线有可能互相垂直
D
过直线外一点向已知直线作垂线时,这一点与垂足之间的线段叫做已知直线的垂线段.
P
O
线段PO是点P到直线m的垂线段
m
垂线段AD的长度叫做点A到直线l的距离
如图,在线段AB、AC、AD、AE中,哪条线段最短?得到什么结论?
1.点到直线的距离是指( )
A.直线外一点到这条直线的垂线段
B.直线外一点到这条直线的垂线段的长度
C.直线外一点到这条直线的垂线的长度
D.直线外一点到这条线上任意一点的距离
B
2、如图,在灌溉时需要把河AB中的水引到C处,如何挖渠能使渠道最短?
A
B
C
D
垂直的定义与表示法
垂线的画法
垂线的性质
点到直线的距离
垂直
1.(西安·中考)如图,点O在直线AB
上,且OC⊥OD,若∠COA=36°,则
∠DOB的大小为( )
A.36° B.54° C.64° D.72°
【解析】选B.因为OC⊥OD,所以∠COD=90°,又因为∠AOB=180°,所以∠DOB=∠AOB-∠COD-∠COA=180°-90°-36°=54°.
2.如图,OD⊥BC,D是垂足,连接OB,有下列说法:
①线段OB是O,B两点的距离
②线段OB的长度是O,B两点的距离
③线段OD是O点到直线BC的距离
④线段OD的长度是O点到直线BC的距离
其中正确的说法有( )个
A.1 B.2 C.3 D.4
O
B
D
C
B
3.如图所示,AC=4,BC=3,AB=5,则点C到
直线AB的距离是 .
【解析】作CD⊥AB,垂足为点D,则CD的长度就是点C到直线AB的距离,三角形ABC的面积为
,即 ,
所以CD=2.4.
【答案】2.4
Best Wish For You
信心源自于努力
同课章节目录
- 第8章 角
- 8.1 角的表示
- 8.2 角的比较
- 8.3 角的度量
- 8.4 对顶角
- 8.5 垂直
- 第9章 平行线
- 9.1 同位角、内错角、同旁内角
- 9.2 平行线和它的画法
- 9.3 平行线的性质
- 9.4 平行线的判定
- 第10章 一次方程组
- 10.1 认识二元一次方程组
- 10.2 二元一次方程组的解法
- 10.3 三元一次方程组
- 10.4 列方程组解应用题
- 第11章 整式的乘除
- 11.1 同底数幂的乘法
- 11.2 积的乘方与幂的乘方
- 11.3 单项式的乘法
- 11.4 多项式乘多项式
- 11.5 同底数幂的除法
- 11.6 零指数幂与负整数指数幂
- 第12章 乘法公式与因式分解
- 12.1 平方差公式
- 12.2 完全平方公式
- 12.3 用提公因式法进行因式分解
- 12.4 用公式法进行因式分解
- 第13章 平面图形的认识
- 13.1 三角形
- 13.2 多边形
- 13.3 圆
- 第14章 位置与坐标
- 14.1 用有序数对表示位置
- 14.2 平面直角坐标系
- 14.3 直角坐标系中的图形
- 14.4 用方向和距离描述两个物体的相对位置
