人教B版(2019)高中数学必修第二册教学课件:第五章 5.4 统计与概率的应用(共16张PPT)
文档属性
| 名称 | 人教B版(2019)高中数学必修第二册教学课件:第五章 5.4 统计与概率的应用(共16张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 1.6MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教B版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-02-14 00:00:00 | ||
图片预览






文档简介
课件16张PPT。 5.4 统计与概率的应用 第五章 统计与概率学习目标1. 了解统计与概率在实际生活中应用的广泛性.
2.会用统计和概率的有关知识解决实际问题.
3.能用统计和概率的方法与思想分析问题.重点:统计与概率知识的应用.
难点:利用统计和概率知识解决实际问题.. 一.本章所学主要内容???????8.事件的独立性P(AB)=P(A)P(B).三.估计盒子中玻璃球的个数 题型一 随机抽样与概率的综合问题
【例1】2019·天津卷]2019年,我国施行个人所得税专项附加扣除办法,涉及子女教育、继续教育、大病医疗、住房贷款利息或者住房租金、赡养老人等六项专项附加扣除.某单位老、中、青员工分别有72,108,120人,现采用分层抽样的方法,从该单位上述员工中抽取25人调查专项附加扣除的享受情况.
(1)应从老、中、青员工中分别抽取多少人?
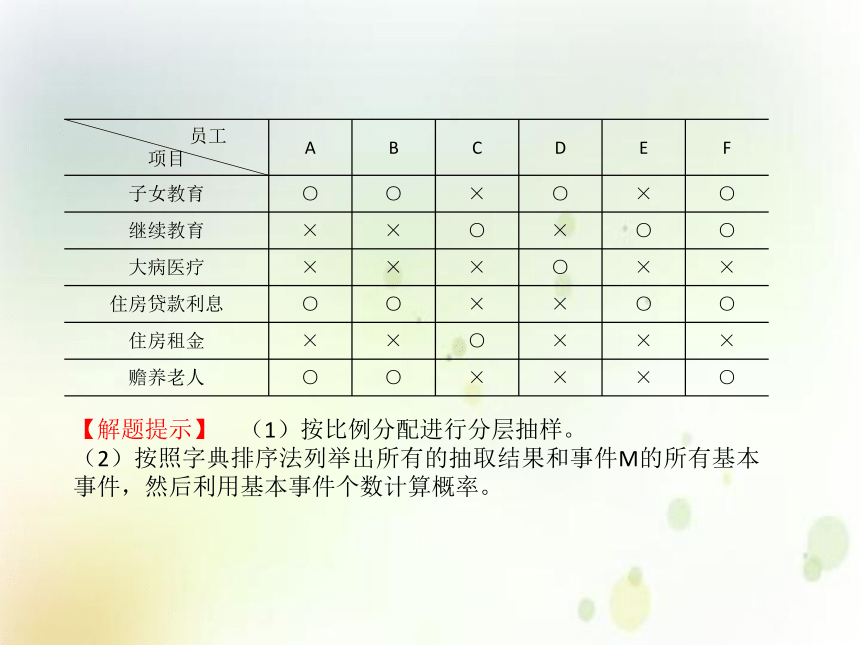
(2)抽取的25人中,享受至少两项专项附加扣除的员工有6人,分别记为A,B,C,D,E,F.享受情况如下表,其中“○”表示享受,“×”表示不享受.现从这6人中随机抽取2人接受采访.
①试用所给字母列举出所有可能的抽取结果;
②设M为事件“抽取的2人享受的专项附加扣除至少有一项相同”,求事件M发生的概率.常考题型【解题提示】 (1)按比例分配进行分层抽样。
(2)按照字典排序法列举出所有的抽取结果和事件M的所有基本事件,然后利用基本事件个数计算概率。【归纳总结】在高考中所考查的概率解答题,一般都是确定好基本事件空间之后,
对基本事件个数用列举法列举,列举时无论使用什么形式,都要注意应用字典排序法
才能不重不漏,因为只要正确列举出来,概率的计算就很简单了。【归纳总结】概率问题常常与频率分布综合考查,求解的方法是利用频率分布求出样本空间中基本事件个数,和所求事件含有多少个基本事件,最后利用古典概型的概率公式求出概率。解题关键是读图识图能力。解:(1)由频率分布直方图可知,月均用水量在[0,0.5)的频率为0.08×0.5=0.04,
同理,在[0.5,1),[1.5,2),[2,2.5),[3,3.5),[3.5,4),[4,4.5]组的频率分别为0.08,0.21,0.25,0.06,0.04,0.02.
由1-(0.04+0.08+0.21+0.25+0.06+0.04+0.02)=0.5×a+0.5×a,解得a=0.30.
(2)由(1)知,该市100位居民中月均用水量不低于3吨的频率为0.06+0.04+0.02=0.12.
由以上样本的频率分布,可以估计30万居民中月均用水量不低于3吨的人数为
300 000×0.12=36 000.
(3)设中位数为x吨.因为前5组的频率之和为0.04+0.08+0.15+0.21+0.25=0.73>0.5,而前4组的频率之和为0.04+0.08+0.15+0.21=0.48<0.5,所以2≤x<2.5.
由0.50×(x-2)=0.5-0.48,解得x=2.04.
故可估计居民月均用水量的中位数为2.04吨. 题型三 比赛中的概率问题1.概率的应用问题是与统计紧密相联系的,因此要熟悉统计中的各种图表的应用,才能正确的解答概率应用问题。
2.概率的实际应用问题,经常把互斥事件的概率与相互独立事件的概率综合起来使用,所以要熟悉概率的加法公式和乘法公式的适用条件。
3.比赛中的概率问题,要注意首先找出事件的和与事件的积,才能正确使用互斥事件的概率加法公式,与独立事件的概率乘法公式。
2.会用统计和概率的有关知识解决实际问题.
3.能用统计和概率的方法与思想分析问题.重点:统计与概率知识的应用.
难点:利用统计和概率知识解决实际问题.. 一.本章所学主要内容???????8.事件的独立性P(AB)=P(A)P(B).三.估计盒子中玻璃球的个数 题型一 随机抽样与概率的综合问题
【例1】2019·天津卷]2019年,我国施行个人所得税专项附加扣除办法,涉及子女教育、继续教育、大病医疗、住房贷款利息或者住房租金、赡养老人等六项专项附加扣除.某单位老、中、青员工分别有72,108,120人,现采用分层抽样的方法,从该单位上述员工中抽取25人调查专项附加扣除的享受情况.
(1)应从老、中、青员工中分别抽取多少人?
(2)抽取的25人中,享受至少两项专项附加扣除的员工有6人,分别记为A,B,C,D,E,F.享受情况如下表,其中“○”表示享受,“×”表示不享受.现从这6人中随机抽取2人接受采访.
①试用所给字母列举出所有可能的抽取结果;
②设M为事件“抽取的2人享受的专项附加扣除至少有一项相同”,求事件M发生的概率.常考题型【解题提示】 (1)按比例分配进行分层抽样。
(2)按照字典排序法列举出所有的抽取结果和事件M的所有基本事件,然后利用基本事件个数计算概率。【归纳总结】在高考中所考查的概率解答题,一般都是确定好基本事件空间之后,
对基本事件个数用列举法列举,列举时无论使用什么形式,都要注意应用字典排序法
才能不重不漏,因为只要正确列举出来,概率的计算就很简单了。【归纳总结】概率问题常常与频率分布综合考查,求解的方法是利用频率分布求出样本空间中基本事件个数,和所求事件含有多少个基本事件,最后利用古典概型的概率公式求出概率。解题关键是读图识图能力。解:(1)由频率分布直方图可知,月均用水量在[0,0.5)的频率为0.08×0.5=0.04,
同理,在[0.5,1),[1.5,2),[2,2.5),[3,3.5),[3.5,4),[4,4.5]组的频率分别为0.08,0.21,0.25,0.06,0.04,0.02.
由1-(0.04+0.08+0.21+0.25+0.06+0.04+0.02)=0.5×a+0.5×a,解得a=0.30.
(2)由(1)知,该市100位居民中月均用水量不低于3吨的频率为0.06+0.04+0.02=0.12.
由以上样本的频率分布,可以估计30万居民中月均用水量不低于3吨的人数为
300 000×0.12=36 000.
(3)设中位数为x吨.因为前5组的频率之和为0.04+0.08+0.15+0.21+0.25=0.73>0.5,而前4组的频率之和为0.04+0.08+0.15+0.21=0.48<0.5,所以2≤x<2.5.
由0.50×(x-2)=0.5-0.48,解得x=2.04.
故可估计居民月均用水量的中位数为2.04吨. 题型三 比赛中的概率问题1.概率的应用问题是与统计紧密相联系的,因此要熟悉统计中的各种图表的应用,才能正确的解答概率应用问题。
2.概率的实际应用问题,经常把互斥事件的概率与相互独立事件的概率综合起来使用,所以要熟悉概率的加法公式和乘法公式的适用条件。
3.比赛中的概率问题,要注意首先找出事件的和与事件的积,才能正确使用互斥事件的概率加法公式,与独立事件的概率乘法公式。
