17.1 勾股定理(第2课时)勾股定理在实际生活中的应用教学课件
文档属性
| 名称 | 17.1 勾股定理(第2课时)勾股定理在实际生活中的应用教学课件 |

|
|
| 格式 | zip | ||
| 文件大小 | 1.6MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-02-14 00:00:00 | ||
图片预览






文档简介
课件22张PPT。2020年春人教版八年级下数学教学课件 17.1 勾股定理(第2课时)
勾股定理在实际生活中的应用12会运用勾股定理求线段长及解决简单的实际问题. (重点) 能从实际问题中抽象出勾股定理的数学模型,并能利用勾股定理建立已知边与未知边长度之间的联系,进一步求出未知边长. (难点)知识回顾勾股定理:直角三角形两直角边的平方和等于斜边的平方.几何语言:
∵在Rt△ABC中 ,∠C=90°,
∴a2+b2=c2(勾股定理).勾股定理揭示了直角三角形三边之间的关系.★ 勾股定理的简单实际应用问题1: 一个门框的尺寸如图所示,一块长3m,宽2.2m的长方形薄木板能否从门框内通过?为什么?分析:可以看出木板无论横着,还是竖着都不能通过,所以只能考虑斜着.观察可以发现 AC的长度是斜着能通过的最大长度,所以只要AC的长大于木板的宽就能通过.解:连接AC,在Rt△ABC中,根据勾股定理,得AC2=AB2+BC2=12+22=5, 因为AC的长大于木板的宽2.2m,
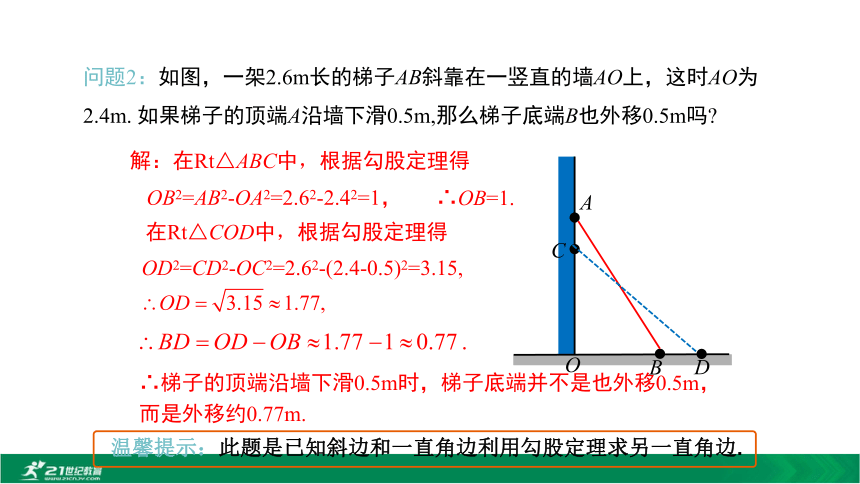
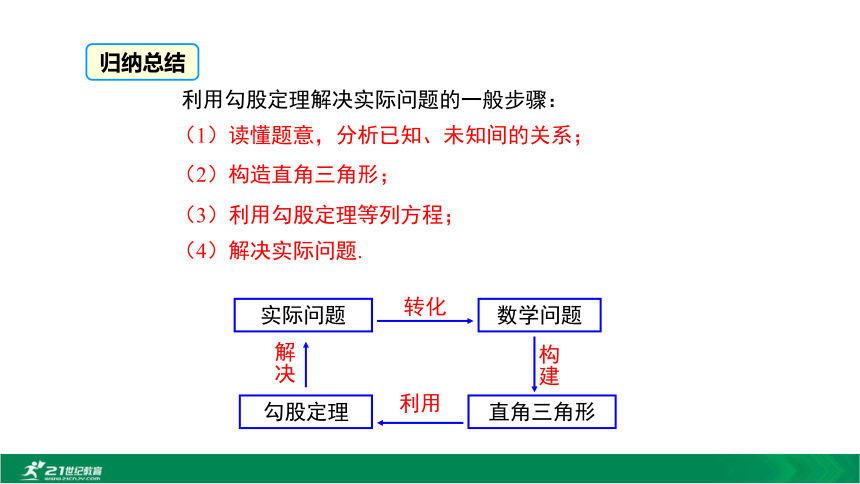
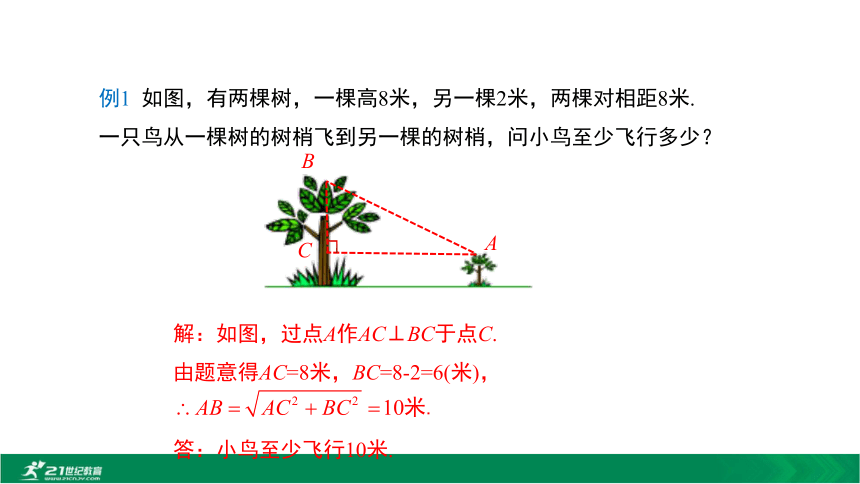
所以木板能从门框内通过. 问题2:如图,一架2.6m长的梯子AB斜靠在一竖直的墙AO上,这时AO为2.4m. 如果梯子的顶端A沿墙下滑0.5m,那么梯子底端B也外移0.5m吗?解:在Rt△ABC中,根据勾股定理得OB2=AB2-OA2=2.62-2.42=1,∴OB=1.在Rt△COD中,根据勾股定理得OD2=CD2-OC2=2.62-(2.4-0.5)2=3.15,∴梯子的顶端沿墙下滑0.5m时,梯子底端并不是也外移0.5m,而是外移约0.77m.利用勾股定理解决实际问题的一般步骤:(1)读懂题意,分析已知、未知间的关系;(2)构造直角三角形;(3)利用勾股定理等列方程;(4)解决实际问题.归纳总结数学问题直角三角形勾股定理实际问题例1 如图,有两棵树,一棵高8米,另一棵2米,两棵对相距8米.一只鸟从一棵树的树梢飞到另一棵的树梢,问小鸟至少飞行多少? ABC解:如图,过点A作AC⊥BC于点C.
由题意得AC=8米,BC=8-2=6(米),
答:小鸟至少飞行10米.★ 利用勾股定理求两点间距离A21-4-3-2-1-123145例2 如图,在平面直角坐标系中有两点A(-3,5),B(1,2)求A,B两点间的距离.yOx3BC解:如图,过点A作x轴的垂线,过点B作x,y轴的垂线.相交于点C,连接AB.
∴AC=5-2=3,BC=3+1=4,
在Rt△ABC中,由勾股定理得
∴A,B两点间的距离为5.方法总结:两点之间的距离公式:一般地,设平面上任意两点
★ 利用勾股定理求最短距离CBAAC+CB >AB(两点之间线段最短)思考: 在立体图形中,应该怎么寻找最短线路呢?想一想:蚂蚁走哪一条路线最近?A' 蚂蚁从A爬到B的路线问题:在一个圆柱石凳上,若小明在吃东西时留下了一点食物在B处,恰好一只在A处的蚂蚁捕捉到这一信息,于是它想从A处爬向B处,蚂蚁怎么走最近?根据两点之间线段最短易知第一个路线最近. 若已知圆柱体高为12 cm,底面半径为3 cm,π取3.侧面展开图A'A' 解:在Rt△ABA′中,由勾股定理得 归纳:立体图形中求两点间的最短距离,一般把立体图形展开成平面图形,连接两点,根据两点之间线段最短确定最短路线.数学思想:立体图形平面图形转化展开例3 如图,长方体的长为10cm,宽为6cm,高为8cm,一只蚂蚁沿着长方体的表面由A爬到B需要爬行的最短路程是多少?BA6cm8cm10cmBB18AB2610B3AB12 =102 +(6+8)2 =296,AB22= 82 +(10+6)2 =320,AB32= 62 +(10+8)2 =360,解:由题意知有三种展开方法,如图.由勾股定理得∴AB1<AB2<AB3.∴小蚂蚁完成任务的最短路程为AB1,长为 .CD1.如图,一棵大树被台风刮断,若树在离地面3m 处折断,树顶端落在离树底部4m处,则树折断之前高( )
A.5m B.7m C.8m D.10m 2.如图,一支铅笔放在圆柱体笔筒中,笔筒的内部底面直径是9cm,内壁高12cm,则这只铅笔的长度可能是( )
A.9cm B.12cm C.15cm D.18cm 1053.甲、乙两人同时从同一地点出发,已知甲往东走了4km,乙往南走了3km,此时甲、乙两人相距______km.4.已知点(3,4),(-5,-4),则这两点的距离为_______.5.如图,是一个三级台阶,它的每一级的长、宽和高分别等于55cm,10cm和6cm,A和B是这个台阶的两个相对的端点,A点上有一只蚂蚁,想到B点去吃可口的食物.这只蚂蚁从A点出发,沿着台阶面爬到B点,最短线路是多少?BA解:台阶的展开图如图,连接AB.在Rt△ABC中,根据勾股定理得AB2=BC2+AC2=552+482=5329,∴AB=73cm.6.如图,一个牧童在小河的南4km的A处牧马,而他正位于他的小屋B的西8km北7km处,他想把他的马牵到小河边去饮水,然后回家.他要完成这件事情所走的最短路程是多少?牧童A小屋BA′C东北解:如图,作出点A关于河岸的对称点A′,连接A′B则A′B就是最短路线.
由题意得A′C=4+4+7=15(km),BC=8km.
在Rt△A′DB中,由勾股定理得勾股定理的应用利用勾股定理解决实际问题利用勾股定理求两点间的距离利用勾股定理求最短距离谢谢21世纪教育网(www.21cnjy.com) 中小学教育资源网站 有大把高质量资料?一线教师?一线教研员?
欢迎加入21世纪教育网教师合作团队!!月薪过万不是梦!!
详情请看:
https://www.21cnjy.com/help/help_extract.php
勾股定理在实际生活中的应用12会运用勾股定理求线段长及解决简单的实际问题. (重点) 能从实际问题中抽象出勾股定理的数学模型,并能利用勾股定理建立已知边与未知边长度之间的联系,进一步求出未知边长. (难点)知识回顾勾股定理:直角三角形两直角边的平方和等于斜边的平方.几何语言:
∵在Rt△ABC中 ,∠C=90°,
∴a2+b2=c2(勾股定理).勾股定理揭示了直角三角形三边之间的关系.★ 勾股定理的简单实际应用问题1: 一个门框的尺寸如图所示,一块长3m,宽2.2m的长方形薄木板能否从门框内通过?为什么?分析:可以看出木板无论横着,还是竖着都不能通过,所以只能考虑斜着.观察可以发现 AC的长度是斜着能通过的最大长度,所以只要AC的长大于木板的宽就能通过.解:连接AC,在Rt△ABC中,根据勾股定理,得AC2=AB2+BC2=12+22=5, 因为AC的长大于木板的宽2.2m,
所以木板能从门框内通过. 问题2:如图,一架2.6m长的梯子AB斜靠在一竖直的墙AO上,这时AO为2.4m. 如果梯子的顶端A沿墙下滑0.5m,那么梯子底端B也外移0.5m吗?解:在Rt△ABC中,根据勾股定理得OB2=AB2-OA2=2.62-2.42=1,∴OB=1.在Rt△COD中,根据勾股定理得OD2=CD2-OC2=2.62-(2.4-0.5)2=3.15,∴梯子的顶端沿墙下滑0.5m时,梯子底端并不是也外移0.5m,而是外移约0.77m.利用勾股定理解决实际问题的一般步骤:(1)读懂题意,分析已知、未知间的关系;(2)构造直角三角形;(3)利用勾股定理等列方程;(4)解决实际问题.归纳总结数学问题直角三角形勾股定理实际问题例1 如图,有两棵树,一棵高8米,另一棵2米,两棵对相距8米.一只鸟从一棵树的树梢飞到另一棵的树梢,问小鸟至少飞行多少? ABC解:如图,过点A作AC⊥BC于点C.
由题意得AC=8米,BC=8-2=6(米),
答:小鸟至少飞行10米.★ 利用勾股定理求两点间距离A21-4-3-2-1-123145例2 如图,在平面直角坐标系中有两点A(-3,5),B(1,2)求A,B两点间的距离.yOx3BC解:如图,过点A作x轴的垂线,过点B作x,y轴的垂线.相交于点C,连接AB.
∴AC=5-2=3,BC=3+1=4,
在Rt△ABC中,由勾股定理得
∴A,B两点间的距离为5.方法总结:两点之间的距离公式:一般地,设平面上任意两点
★ 利用勾股定理求最短距离CBAAC+CB >AB(两点之间线段最短)思考: 在立体图形中,应该怎么寻找最短线路呢?想一想:蚂蚁走哪一条路线最近?A' 蚂蚁从A爬到B的路线问题:在一个圆柱石凳上,若小明在吃东西时留下了一点食物在B处,恰好一只在A处的蚂蚁捕捉到这一信息,于是它想从A处爬向B处,蚂蚁怎么走最近?根据两点之间线段最短易知第一个路线最近. 若已知圆柱体高为12 cm,底面半径为3 cm,π取3.侧面展开图A'A' 解:在Rt△ABA′中,由勾股定理得 归纳:立体图形中求两点间的最短距离,一般把立体图形展开成平面图形,连接两点,根据两点之间线段最短确定最短路线.数学思想:立体图形平面图形转化展开例3 如图,长方体的长为10cm,宽为6cm,高为8cm,一只蚂蚁沿着长方体的表面由A爬到B需要爬行的最短路程是多少?BA6cm8cm10cmBB18AB2610B3AB12 =102 +(6+8)2 =296,AB22= 82 +(10+6)2 =320,AB32= 62 +(10+8)2 =360,解:由题意知有三种展开方法,如图.由勾股定理得∴AB1<AB2<AB3.∴小蚂蚁完成任务的最短路程为AB1,长为 .CD1.如图,一棵大树被台风刮断,若树在离地面3m 处折断,树顶端落在离树底部4m处,则树折断之前高( )
A.5m B.7m C.8m D.10m 2.如图,一支铅笔放在圆柱体笔筒中,笔筒的内部底面直径是9cm,内壁高12cm,则这只铅笔的长度可能是( )
A.9cm B.12cm C.15cm D.18cm 1053.甲、乙两人同时从同一地点出发,已知甲往东走了4km,乙往南走了3km,此时甲、乙两人相距______km.4.已知点(3,4),(-5,-4),则这两点的距离为_______.5.如图,是一个三级台阶,它的每一级的长、宽和高分别等于55cm,10cm和6cm,A和B是这个台阶的两个相对的端点,A点上有一只蚂蚁,想到B点去吃可口的食物.这只蚂蚁从A点出发,沿着台阶面爬到B点,最短线路是多少?BA解:台阶的展开图如图,连接AB.在Rt△ABC中,根据勾股定理得AB2=BC2+AC2=552+482=5329,∴AB=73cm.6.如图,一个牧童在小河的南4km的A处牧马,而他正位于他的小屋B的西8km北7km处,他想把他的马牵到小河边去饮水,然后回家.他要完成这件事情所走的最短路程是多少?牧童A小屋BA′C东北解:如图,作出点A关于河岸的对称点A′,连接A′B则A′B就是最短路线.
由题意得A′C=4+4+7=15(km),BC=8km.
在Rt△A′DB中,由勾股定理得勾股定理的应用利用勾股定理解决实际问题利用勾股定理求两点间的距离利用勾股定理求最短距离谢谢21世纪教育网(www.21cnjy.com) 中小学教育资源网站 有大把高质量资料?一线教师?一线教研员?
欢迎加入21世纪教育网教师合作团队!!月薪过万不是梦!!
详情请看:
https://www.21cnjy.com/help/help_extract.php
