17.2 勾股定理的逆定理(第1课时)勾股定理的逆定理教学课件
文档属性
| 名称 | 17.2 勾股定理的逆定理(第1课时)勾股定理的逆定理教学课件 |  | |
| 格式 | zip | ||
| 文件大小 | 1.6MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-02-14 18:02:39 | ||
图片预览





文档简介
课件26张PPT。2020年春人教版八年级下数学教学课件 17.2 勾股定理的逆定理(第1课时)
勾股定理的逆定理12能掌握勾股定理的逆定理的,并了解互逆命题、定理的概念、关系及勾股数. (重点)能利用勾股定理的逆定理判断一个三角形是直角三角形. (难点) 复习引入 问题1:勾股定理的内容是什么? 如果直角三角形的两条直角边长分别为a,b,斜边为c,那么a2+b2=c2.bca问题2:求以线段a、b为直角边的直角三角形的斜边c的长:① a=3,b=4;
② a=2.5,b=6;
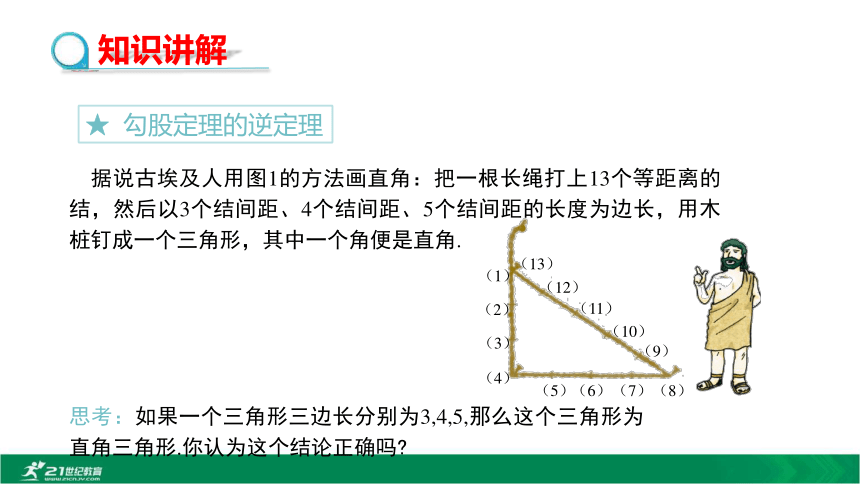
③ a=4,b=7.5.c=5c=6.5c=8.5思考 :以前我们已经学过了通过角的关系来确定直角三角形,可不可以通过边来确定直角三角形呢?★ 勾股定理的逆定理 据说古埃及人用图1的方法画直角:把一根长绳打上13个等距离的结,然后以3个结间距、4个结间距、5个结间距的长度为边长,用木桩钉成一个三角形,其中一个角便是直角. 思考:如果一个三角形三边长分别为3,4,5,那么这个三角形为直角三角形.你认为这个结论正确吗?下面有三组数分别是一个三角形的三边长a, b, c:
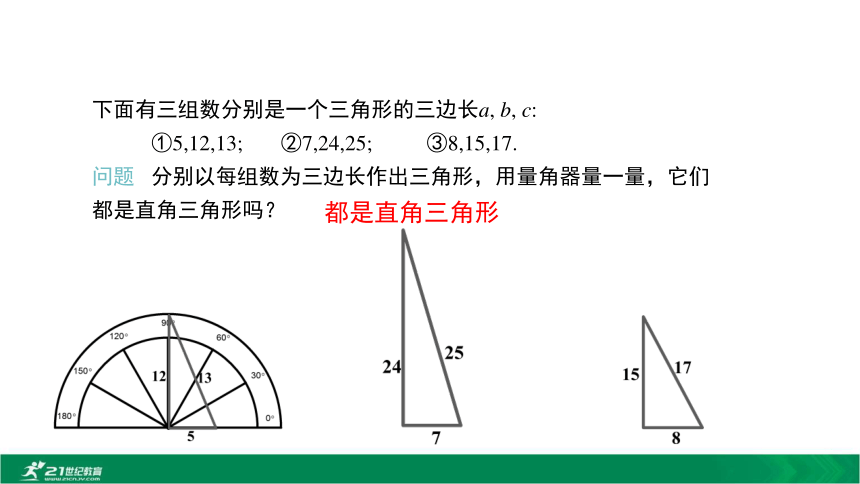
①5,12,13; ②7,24,25; ③8,15,17.
问题 分别以每组数为三边长作出三角形,用量角器量一量,它们都是直角三角形吗?都是直角三角形下面有三组数分别是一个三角形的三边长a, b, c.
①5,12,13; ②7,24,25; ③8,15,17.
问题:这三组数在数量关系上有什么相同点?① 5,12,13满足52+122=132,
② 7,24,25满足72+242=252,
③ 8,15,17满足82+152=172.a2+b2=c2猜想:
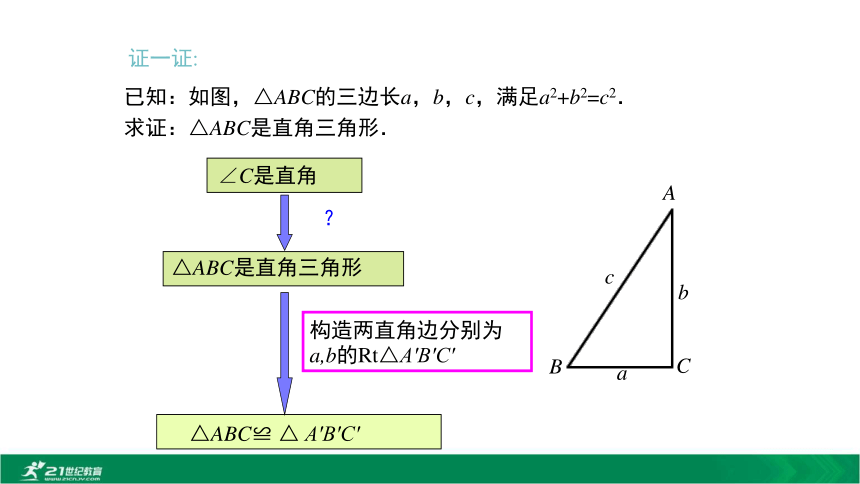
命题2 如果三角形的三边长a,b,c满足a2+b2=c2,那么这个三角形是直角三角形.? 已知:如图,△ABC的三边长a,b,c,满足a2+b2=c2.
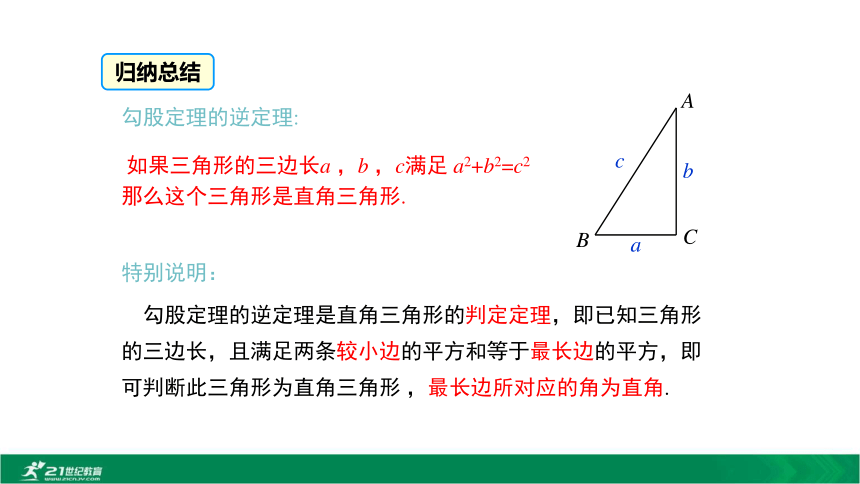
求证:△ABC是直角三角形.构造两直角边分别为a,b的Rt△A′B′C′证一证:证明:作Rt△A′B′C′,使∠C′=90°,A′C′=b,B′C′=a,∴△ABC≌ △A′B′C′(SSS),∴∠C= ∠C′=90° , 即△ABC是直角三角形.勾股定理的逆定理: 如果三角形的三边长a ,b ,c满足 a2+b2=c2
那么这个三角形是直角三角形. 勾股定理的逆定理是直角三角形的判定定理,即已知三角形的三边长,且满足两条较小边的平方和等于最长边的平方,即可判断此三角形为直角三角形 ,最长边所对应的角为直角.特别说明:归纳总结 例1 下面以a,b,c为边长的三角形是不是直角三角形?如果是,那么哪一个角是直角?(1) a=15 , b=8 ,c=17; 解:(1)∵152+82=289,172=289,∴152+82=172,
根据勾股定理的逆定理,这个三角形是直角三角形,
且∠C是直角.(2) a=13 ,b=14 ,c=15. (2)∵132+142=365,152=225,
∴132+142≠152,不符合勾股定理的逆定理,
∴这个三角形不是直角三角形.运用勾股定理的逆定理判断直角三角形的一般步骤:
(1)找:确定三角形的最长边;
(2)算:分别计算出最长边的平方与另两边的平方和;
(3)比:通过比较来判断最长边的平方与另两边的平方和是否相等;
(4)判:作出结论,若相等,则说明这个三角形是直角三角形,否则不是直角三角形. 方法技巧:例2 判断满足下列条件的三角形是否为直角三角形.
(1)在△ABC 中,∠A = 20°,∠B = 70°;
(2)在△ABC 中,AC=7,AB=24,BC=25 ;
(3)一个三角形的三边长a,b,c 满足(a+b)(a-b)= c2. ?判定三角形为直角三角形的方法
(1)用角判断:
①两个锐角互余的三角形是直角三角形;
②有一个角是90°的三角形是直角三角形;
(2)用边判断:如果已知条件与边有关,则可通过勾股定理的逆定理进行判断. 方法技巧:★ 勾股数 如果三角形的三边长a,b,c满足a2+b2=c2,那么这个三角形是直角三角形.满足a2+b2=c2的三个正整数,称为勾股数.常见勾股数:3,4,5;5,12,13;6,8,10;7,24,25;8,15,17;9,40,41;10,24,26等等.勾股数拓展性质: 一组勾股数,都扩大相同倍数k(k为正整数),得到一组新数,这组数同样是勾股数.例3 下列几组数为勾股数的是( )
A.4,5,6 B.12,16,20
C.-10,24,26 D.2.4,4.5,5.1 解析:B★ 互逆命题与互逆定理命题1 如果直角三角形的两条直角边长分别为a,b,斜边为c,那么a2+b2=c2. 命题2 如果三角形的三边长a 、b 、c满足a2+b2=c2,那么这个三角形是直角三角形.前面我们学习了两个命题,分别为:命题1:直角三角形a2+b2=c2命题2:直角三角形a2+b2=c2题设结论它们是题设和结论正好相反的两个命题.问题1:两个命题的条件和结论分别是什么?问题2:两个命题的条件和结论有何联系? 一般地,原命题成立时,它的逆命题既可能成立,也可能不成立.如果一个定理的逆命题经过证明是正确的,那么它也是一个定理,我们称这两个定理互为逆定理.勾股定理与勾股定理的逆定理为互逆定理. 题设和结论正好相反的两个命题,叫做互逆命题,其中一个叫做原命题,另一个叫做原命题的逆命题.归纳总结例4 说出下列命题的逆命题,这些逆命题成立吗?
(1)两条直线平行,内错角相等;
(2)如果两个实数的绝对值相等,那么这两个实数的平方相等;
(3) 对顶角相等;
(4)在角的内部,到角的两边距离相等的点在角的平分线上.内错角相等,两条直线平行.如果两个实数的平方相等,那么这两个实数的绝对值相等.如果两个角相等,那么这两个角是对顶角. 在角平分线上的点到角的两边距离相等. 成立成立不成立成立 1.下列各组数是勾股数的是 ( )
A.6,8,10 B.7,8,9
C.0.3,0.4,0.5 D.52,122,132A ?C 3.下列定理中,有逆定理的个数是( )
①有两边相等的三角形是等腰三角形;②若三角形的三边长a,b,c满足a2+b2=c2,则该三角形是直角三角形;③全等三角形的对应角相等;④若a=b, a2 =b2.
A. 1个 B. 2个 C. 3个 D. 4个B 4.△ABC的两边a,b分别为5,12,另一边c为奇数,且a+b+c是3的倍数,则c应为______,此三角形为 .13直角三角形5.已知△ABC,AB=n2-1,BC=2n,AC=n2+1(n为大
于1的正整数).试问△ABC是直角三角形吗?若是,
哪一条边所对的角是直角?请说明理由.解:∵AB2+BC2=(n2-1)2+(2n)2
=n4 -2n2+1+4n2
=n4 +2n2+1
=(n2+1)2
=AC2,
∴△ABC直角三角形,边AC所对的角是直角. 6.如图,在四边形ABCD中,AB=8,BC=6,AC=10,AD=CD= , 求四边形ABCD 的面积.∴ △ ABC是直角三角形且∠B是直角.∴ △ ADC是直角三角形且∠ D是直角,∴S 四边形 ABCD=勾股定理的逆定理内容如果三角形的三边长a ,b ,c满足 a2+b2=c2,那么这个三角形是直角三角形.注意最长边不一定是c, ∠C也不一定是直角作用:从三边数量关系判定一个三角形是否是直角形三角形勾股数满足a2+b2=c2的三个正整数,称为勾股数.谢谢21世纪教育网(www.21cnjy.com) 中小学教育资源网站 有大把高质量资料?一线教师?一线教研员?
欢迎加入21世纪教育网教师合作团队!!月薪过万不是梦!!
详情请看:
https://www.21cnjy.com/help/help_extract.php
勾股定理的逆定理12能掌握勾股定理的逆定理的,并了解互逆命题、定理的概念、关系及勾股数. (重点)能利用勾股定理的逆定理判断一个三角形是直角三角形. (难点) 复习引入 问题1:勾股定理的内容是什么? 如果直角三角形的两条直角边长分别为a,b,斜边为c,那么a2+b2=c2.bca问题2:求以线段a、b为直角边的直角三角形的斜边c的长:① a=3,b=4;
② a=2.5,b=6;
③ a=4,b=7.5.c=5c=6.5c=8.5思考 :以前我们已经学过了通过角的关系来确定直角三角形,可不可以通过边来确定直角三角形呢?★ 勾股定理的逆定理 据说古埃及人用图1的方法画直角:把一根长绳打上13个等距离的结,然后以3个结间距、4个结间距、5个结间距的长度为边长,用木桩钉成一个三角形,其中一个角便是直角. 思考:如果一个三角形三边长分别为3,4,5,那么这个三角形为直角三角形.你认为这个结论正确吗?下面有三组数分别是一个三角形的三边长a, b, c:
①5,12,13; ②7,24,25; ③8,15,17.
问题 分别以每组数为三边长作出三角形,用量角器量一量,它们都是直角三角形吗?都是直角三角形下面有三组数分别是一个三角形的三边长a, b, c.
①5,12,13; ②7,24,25; ③8,15,17.
问题:这三组数在数量关系上有什么相同点?① 5,12,13满足52+122=132,
② 7,24,25满足72+242=252,
③ 8,15,17满足82+152=172.a2+b2=c2猜想:
命题2 如果三角形的三边长a,b,c满足a2+b2=c2,那么这个三角形是直角三角形.? 已知:如图,△ABC的三边长a,b,c,满足a2+b2=c2.
求证:△ABC是直角三角形.构造两直角边分别为a,b的Rt△A′B′C′证一证:证明:作Rt△A′B′C′,使∠C′=90°,A′C′=b,B′C′=a,∴△ABC≌ △A′B′C′(SSS),∴∠C= ∠C′=90° , 即△ABC是直角三角形.勾股定理的逆定理: 如果三角形的三边长a ,b ,c满足 a2+b2=c2
那么这个三角形是直角三角形. 勾股定理的逆定理是直角三角形的判定定理,即已知三角形的三边长,且满足两条较小边的平方和等于最长边的平方,即可判断此三角形为直角三角形 ,最长边所对应的角为直角.特别说明:归纳总结 例1 下面以a,b,c为边长的三角形是不是直角三角形?如果是,那么哪一个角是直角?(1) a=15 , b=8 ,c=17; 解:(1)∵152+82=289,172=289,∴152+82=172,
根据勾股定理的逆定理,这个三角形是直角三角形,
且∠C是直角.(2) a=13 ,b=14 ,c=15. (2)∵132+142=365,152=225,
∴132+142≠152,不符合勾股定理的逆定理,
∴这个三角形不是直角三角形.运用勾股定理的逆定理判断直角三角形的一般步骤:
(1)找:确定三角形的最长边;
(2)算:分别计算出最长边的平方与另两边的平方和;
(3)比:通过比较来判断最长边的平方与另两边的平方和是否相等;
(4)判:作出结论,若相等,则说明这个三角形是直角三角形,否则不是直角三角形. 方法技巧:例2 判断满足下列条件的三角形是否为直角三角形.
(1)在△ABC 中,∠A = 20°,∠B = 70°;
(2)在△ABC 中,AC=7,AB=24,BC=25 ;
(3)一个三角形的三边长a,b,c 满足(a+b)(a-b)= c2. ?判定三角形为直角三角形的方法
(1)用角判断:
①两个锐角互余的三角形是直角三角形;
②有一个角是90°的三角形是直角三角形;
(2)用边判断:如果已知条件与边有关,则可通过勾股定理的逆定理进行判断. 方法技巧:★ 勾股数 如果三角形的三边长a,b,c满足a2+b2=c2,那么这个三角形是直角三角形.满足a2+b2=c2的三个正整数,称为勾股数.常见勾股数:3,4,5;5,12,13;6,8,10;7,24,25;8,15,17;9,40,41;10,24,26等等.勾股数拓展性质: 一组勾股数,都扩大相同倍数k(k为正整数),得到一组新数,这组数同样是勾股数.例3 下列几组数为勾股数的是( )
A.4,5,6 B.12,16,20
C.-10,24,26 D.2.4,4.5,5.1 解析:B★ 互逆命题与互逆定理命题1 如果直角三角形的两条直角边长分别为a,b,斜边为c,那么a2+b2=c2. 命题2 如果三角形的三边长a 、b 、c满足a2+b2=c2,那么这个三角形是直角三角形.前面我们学习了两个命题,分别为:命题1:直角三角形a2+b2=c2命题2:直角三角形a2+b2=c2题设结论它们是题设和结论正好相反的两个命题.问题1:两个命题的条件和结论分别是什么?问题2:两个命题的条件和结论有何联系? 一般地,原命题成立时,它的逆命题既可能成立,也可能不成立.如果一个定理的逆命题经过证明是正确的,那么它也是一个定理,我们称这两个定理互为逆定理.勾股定理与勾股定理的逆定理为互逆定理. 题设和结论正好相反的两个命题,叫做互逆命题,其中一个叫做原命题,另一个叫做原命题的逆命题.归纳总结例4 说出下列命题的逆命题,这些逆命题成立吗?
(1)两条直线平行,内错角相等;
(2)如果两个实数的绝对值相等,那么这两个实数的平方相等;
(3) 对顶角相等;
(4)在角的内部,到角的两边距离相等的点在角的平分线上.内错角相等,两条直线平行.如果两个实数的平方相等,那么这两个实数的绝对值相等.如果两个角相等,那么这两个角是对顶角. 在角平分线上的点到角的两边距离相等. 成立成立不成立成立 1.下列各组数是勾股数的是 ( )
A.6,8,10 B.7,8,9
C.0.3,0.4,0.5 D.52,122,132A ?C 3.下列定理中,有逆定理的个数是( )
①有两边相等的三角形是等腰三角形;②若三角形的三边长a,b,c满足a2+b2=c2,则该三角形是直角三角形;③全等三角形的对应角相等;④若a=b, a2 =b2.
A. 1个 B. 2个 C. 3个 D. 4个B 4.△ABC的两边a,b分别为5,12,另一边c为奇数,且a+b+c是3的倍数,则c应为______,此三角形为 .13直角三角形5.已知△ABC,AB=n2-1,BC=2n,AC=n2+1(n为大
于1的正整数).试问△ABC是直角三角形吗?若是,
哪一条边所对的角是直角?请说明理由.解:∵AB2+BC2=(n2-1)2+(2n)2
=n4 -2n2+1+4n2
=n4 +2n2+1
=(n2+1)2
=AC2,
∴△ABC直角三角形,边AC所对的角是直角. 6.如图,在四边形ABCD中,AB=8,BC=6,AC=10,AD=CD= , 求四边形ABCD 的面积.∴ △ ABC是直角三角形且∠B是直角.∴ △ ADC是直角三角形且∠ D是直角,∴S 四边形 ABCD=勾股定理的逆定理内容如果三角形的三边长a ,b ,c满足 a2+b2=c2,那么这个三角形是直角三角形.注意最长边不一定是c, ∠C也不一定是直角作用:从三边数量关系判定一个三角形是否是直角形三角形勾股数满足a2+b2=c2的三个正整数,称为勾股数.谢谢21世纪教育网(www.21cnjy.com) 中小学教育资源网站 有大把高质量资料?一线教师?一线教研员?
欢迎加入21世纪教育网教师合作团队!!月薪过万不是梦!!
详情请看:
https://www.21cnjy.com/help/help_extract.php
