17.2 勾股定理的逆定理(第2课时)勾股定理的逆定理的应用教学课件
文档属性
| 名称 | 17.2 勾股定理的逆定理(第2课时)勾股定理的逆定理的应用教学课件 |  | |
| 格式 | zip | ||
| 文件大小 | 1.5MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-02-14 18:02:56 | ||
图片预览



文档简介
课件17张PPT。2020年春人教版八年级下数学教学课件 17.2 勾股定理的逆定理(第1课时)
勾股定理的逆定理12灵活应用勾股定理及其逆定理解决实际问题. (重点)能将实际问题转化成用勾股定理的逆定理解决的数学问题.(难点) 知识回顾前面的学习让我们对勾股定理及其逆定理的知识有了一定的认识,你能说出它们的内容吗? a2+b2=c2
(a,b为直角边,c斜边)Rt△ABC,∠C是直角勾股定理勾股定理的逆定理a2+b2=c2
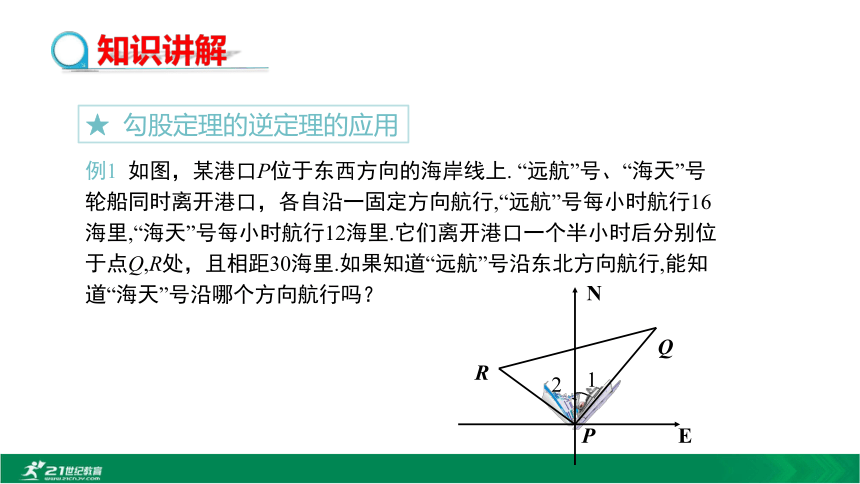
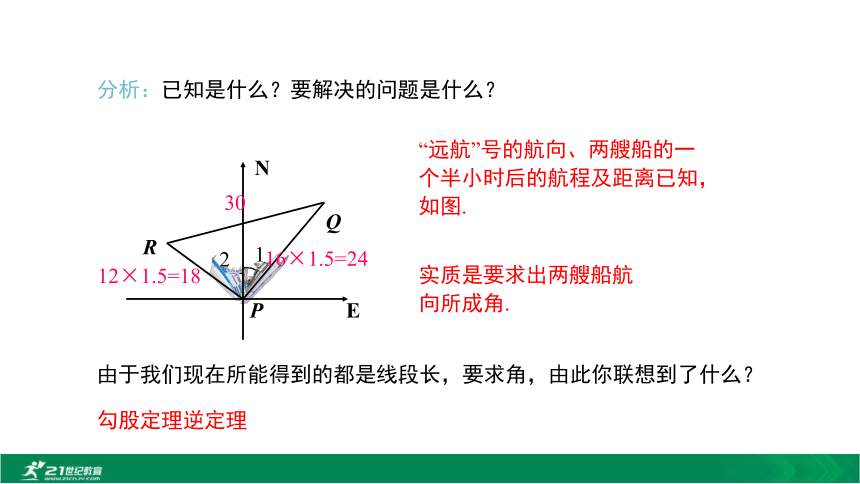
(a,b为较短边,c为最长边)Rt△ABC,且∠C是直角.★ 勾股定理的逆定理的应用例1 如图,某港口P位于东西方向的海岸线上. “远航”号、“海天”号轮船同时离开港口,各自沿一固定方向航行,“远航”号每小时航行16海里,“海天”号每小时航行12海里.它们离开港口一个半小时后分别位于点Q,R处,且相距30海里.如果知道“远航”号沿东北方向航行,能知道“海天”号沿哪个方向航行吗?12NEP QR分析:已知是什么?要解决的问题是什么?12NEP QR16×1.5=2412×1.5=1830“远航”号的航向、两艘船的一个半小时后的航程及距离已知,如图.由于我们现在所能得到的都是线段长,要求角,由此你联想到了什么?实质是要求出两艘船航
向所成角.勾股定理逆定理解:根据题意得PQ=16×1.5=24(海里),PR=12×1.5=18(海里),QR=30海里.∵242+182=302,即PQ2+PR2=QR2,∴∠QPR=90°. 由“远航”号沿东北方向航行可知∠1=45°.
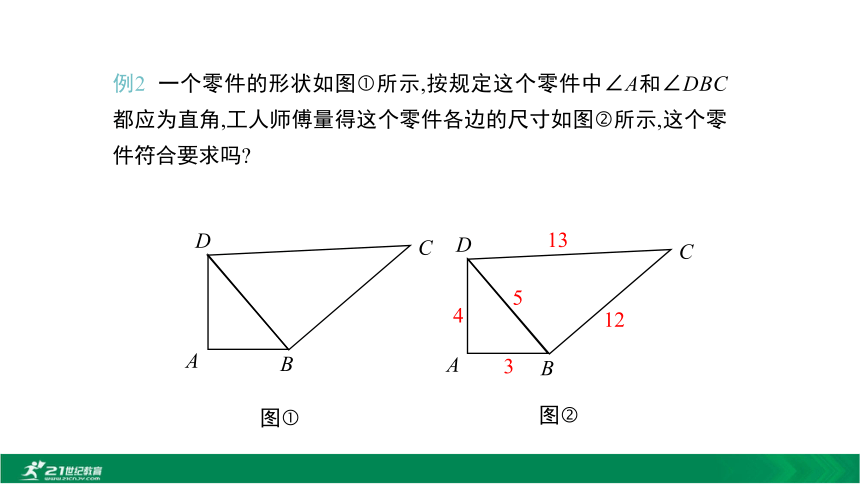
∴∠2=45°,即“海天”号沿西北方向航行. 总结:解决实际问题的步骤:?构建几何模型(从整体到局部);?标注有用信息,明确已知和所求;?应用数学知识求解.例2 一个零件的形状如图?所示,按规定这个零件中∠A和∠DBC都应为直角,工人师傅量得这个零件各边的尺寸如图?所示,这个零件符合要求吗?DABC4351312DABC图?图?在△BCD中,
∴△BCD 是直角三角形,∠DBC是直角.
因此,这个零件符合要求.解:在△ABD中,
∴△ABD 是直角三角形,∠A是直角.DABC4351312★ 勾股定理及其逆定理的综合应用x例3 如图,四边形ABCD中,∠B=90°,AB=3,BC=4,CD=12,AD=13,求四边形ABCD的面积.解:连接AC.在Rt△ABC中,
在△ACD中,
AC2+CD2=52+122=169=AD2,
∴△ACD是直角三角形,
且∠ACD=90°.
∴S四边形ABCD=SRt△ABC+SRt△ACD=6+30=36.例4 如图,四边形ABCD中,AB⊥AD,已知AD=3cm,AB=4cm,CD=12cm,BC=13cm,求四边形ABCD 的面积.CBAD? 1.A、B、C三地的两两距离如图所示,A地在B地的正东方向,C在B地的什么方向?解:∵ BC2+AB2=52+122=169,
AC2 =132=169,
∴BC2+AB2=AC2,
即△ABC是直角三角形,
∠B=90°.
答:C在B地的正北方向.2.如图,在四边形ABCD中,AC⊥DC,△ADC的面积为30 cm2,DC=12 cm,AB=3cm,BC=4cm,求△ABC的面积. 解: ∵ S△ACD=30 cm2,DC=12 cm.
∴ AC=5 cm.
又∵
∴△ABC是直角三角形, ∠B是直角.
∴3.如图,在一次夏令营中,小明从营地A出发,沿北偏东53°方向走了400m到达点B,然后再沿北偏西37°方向走了300m到达目的地C.求A、C两点之间的距离.解:如图,过点B作BE∥AD.
∴∠DAB=∠ABE=53°.
∵37°+∠CBA+∠ABE=180°,
∴∠CBA=90°,
∴AC2=BC2+AB2=3002+4002=5002,
∴AC=500m,
即A、C两点间的距离为500m.解:设AB为3xcm,BC为4xcm,AC为5xcm,
∵周长为36cm,即AB+BC+AC=36cm,
∴3x+4x+5x=36,解得x=3.
∴AB=9cm,BC=12cm,AC=15cm.
∵AB2+BC2=AC2,
∴△ABC是直角三角形,
过3秒时,BP=9-3×2=3(cm),BQ=12-1×3=9(cm),
在Rt△PBQ中,由勾股定理得4.如图,在△ABC中,AB:BC:CA=3:4:5且周长为36cm,点P从点A开始沿AB边向B点以每秒2cm的速度移动,点Q从点C沿CB边向点B以每秒1cm的速度移动,如果同时出发,则过3s时,求PQ的长.勾股定理的逆定理的应用应用航海问题方法认真审题,画出符合题意的图形,熟练运用勾股定理及其逆定理来解决问题与勾股定理结合解决不规则图形等问题谢谢21世纪教育网(www.21cnjy.com) 中小学教育资源网站 有大把高质量资料?一线教师?一线教研员?
欢迎加入21世纪教育网教师合作团队!!月薪过万不是梦!!
详情请看:
https://www.21cnjy.com/help/help_extract.php
勾股定理的逆定理12灵活应用勾股定理及其逆定理解决实际问题. (重点)能将实际问题转化成用勾股定理的逆定理解决的数学问题.(难点) 知识回顾前面的学习让我们对勾股定理及其逆定理的知识有了一定的认识,你能说出它们的内容吗? a2+b2=c2
(a,b为直角边,c斜边)Rt△ABC,∠C是直角勾股定理勾股定理的逆定理a2+b2=c2
(a,b为较短边,c为最长边)Rt△ABC,且∠C是直角.★ 勾股定理的逆定理的应用例1 如图,某港口P位于东西方向的海岸线上. “远航”号、“海天”号轮船同时离开港口,各自沿一固定方向航行,“远航”号每小时航行16海里,“海天”号每小时航行12海里.它们离开港口一个半小时后分别位于点Q,R处,且相距30海里.如果知道“远航”号沿东北方向航行,能知道“海天”号沿哪个方向航行吗?12NEP QR分析:已知是什么?要解决的问题是什么?12NEP QR16×1.5=2412×1.5=1830“远航”号的航向、两艘船的一个半小时后的航程及距离已知,如图.由于我们现在所能得到的都是线段长,要求角,由此你联想到了什么?实质是要求出两艘船航
向所成角.勾股定理逆定理解:根据题意得PQ=16×1.5=24(海里),PR=12×1.5=18(海里),QR=30海里.∵242+182=302,即PQ2+PR2=QR2,∴∠QPR=90°. 由“远航”号沿东北方向航行可知∠1=45°.
∴∠2=45°,即“海天”号沿西北方向航行. 总结:解决实际问题的步骤:?构建几何模型(从整体到局部);?标注有用信息,明确已知和所求;?应用数学知识求解.例2 一个零件的形状如图?所示,按规定这个零件中∠A和∠DBC都应为直角,工人师傅量得这个零件各边的尺寸如图?所示,这个零件符合要求吗?DABC4351312DABC图?图?在△BCD中,
∴△BCD 是直角三角形,∠DBC是直角.
因此,这个零件符合要求.解:在△ABD中,
∴△ABD 是直角三角形,∠A是直角.DABC4351312★ 勾股定理及其逆定理的综合应用x例3 如图,四边形ABCD中,∠B=90°,AB=3,BC=4,CD=12,AD=13,求四边形ABCD的面积.解:连接AC.在Rt△ABC中,
在△ACD中,
AC2+CD2=52+122=169=AD2,
∴△ACD是直角三角形,
且∠ACD=90°.
∴S四边形ABCD=SRt△ABC+SRt△ACD=6+30=36.例4 如图,四边形ABCD中,AB⊥AD,已知AD=3cm,AB=4cm,CD=12cm,BC=13cm,求四边形ABCD 的面积.CBAD? 1.A、B、C三地的两两距离如图所示,A地在B地的正东方向,C在B地的什么方向?解:∵ BC2+AB2=52+122=169,
AC2 =132=169,
∴BC2+AB2=AC2,
即△ABC是直角三角形,
∠B=90°.
答:C在B地的正北方向.2.如图,在四边形ABCD中,AC⊥DC,△ADC的面积为30 cm2,DC=12 cm,AB=3cm,BC=4cm,求△ABC的面积. 解: ∵ S△ACD=30 cm2,DC=12 cm.
∴ AC=5 cm.
又∵
∴△ABC是直角三角形, ∠B是直角.
∴3.如图,在一次夏令营中,小明从营地A出发,沿北偏东53°方向走了400m到达点B,然后再沿北偏西37°方向走了300m到达目的地C.求A、C两点之间的距离.解:如图,过点B作BE∥AD.
∴∠DAB=∠ABE=53°.
∵37°+∠CBA+∠ABE=180°,
∴∠CBA=90°,
∴AC2=BC2+AB2=3002+4002=5002,
∴AC=500m,
即A、C两点间的距离为500m.解:设AB为3xcm,BC为4xcm,AC为5xcm,
∵周长为36cm,即AB+BC+AC=36cm,
∴3x+4x+5x=36,解得x=3.
∴AB=9cm,BC=12cm,AC=15cm.
∵AB2+BC2=AC2,
∴△ABC是直角三角形,
过3秒时,BP=9-3×2=3(cm),BQ=12-1×3=9(cm),
在Rt△PBQ中,由勾股定理得4.如图,在△ABC中,AB:BC:CA=3:4:5且周长为36cm,点P从点A开始沿AB边向B点以每秒2cm的速度移动,点Q从点C沿CB边向点B以每秒1cm的速度移动,如果同时出发,则过3s时,求PQ的长.勾股定理的逆定理的应用应用航海问题方法认真审题,画出符合题意的图形,熟练运用勾股定理及其逆定理来解决问题与勾股定理结合解决不规则图形等问题谢谢21世纪教育网(www.21cnjy.com) 中小学教育资源网站 有大把高质量资料?一线教师?一线教研员?
欢迎加入21世纪教育网教师合作团队!!月薪过万不是梦!!
详情请看:
https://www.21cnjy.com/help/help_extract.php
