3.1.1空间向量及其加减运算(共37张PPT)
文档属性
| 名称 | 3.1.1空间向量及其加减运算(共37张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 1.6MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-02-14 15:29:36 | ||
图片预览









文档简介
(共37张PPT)
复习平面向量
(1)什么是平面向量的定义?
(2)平面向量如何表示?
(3)什么是相等的向量?
(1)既有大小又有方向的量叫向量;
(2)向量有两种表示方法:
①几何表示法:用有向线段表示;
②字母表示法:用字母 等或者用有向线段的起点与终点字母AB表示.
(3)长度相等且方向相同的向量.
解答
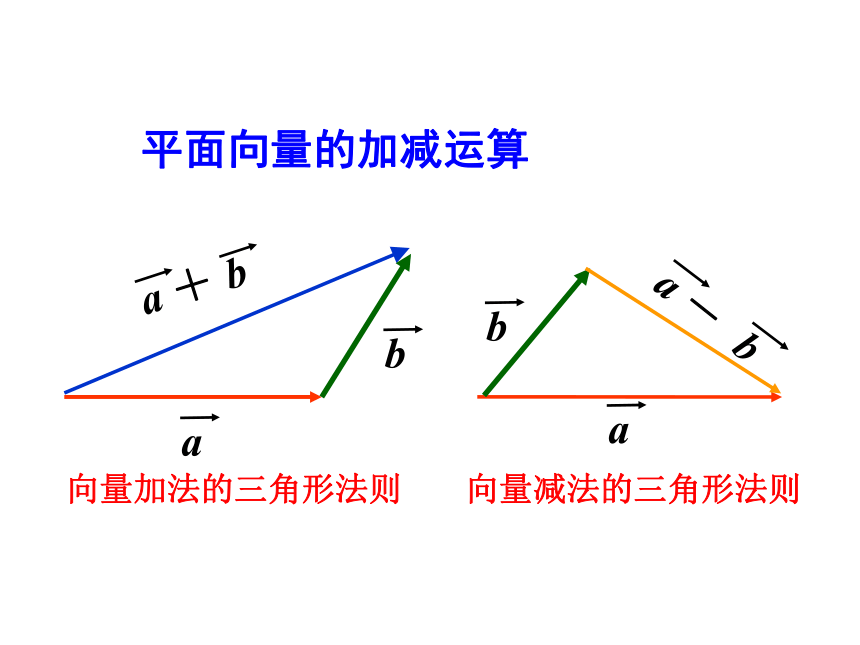
平面向量的加减运算
看下面建筑
这个建筑钢架中有很多向量,但他们有些并不在同一平面内——这就是我们今天要学习的空间向量.
1. 空间向量
在空间,我们把具有大小和方向的量叫做空间向量(space vetor ).
向量的大小叫做向量的长度或模 (modulus).
2. 空间向量的表示
(1)我们规定,长度为0的向量叫做零向量(zero vector),记为0.当有向线段的起点A与终点B重合时,AB=0;
(2)模为1的向量称为单位向量(unit vector);
(3)两个向量不能比较大小,因为决定向量的两个因素是大小和方向,其中方向不能比较大小.
3. 相反向量
与向量 a 长度相等而方向相反的向量,称为 a 的相反向量,记为 – a .
4. 相等向量(equal vetor)
方向相同且模相等的向量称为相等向量.
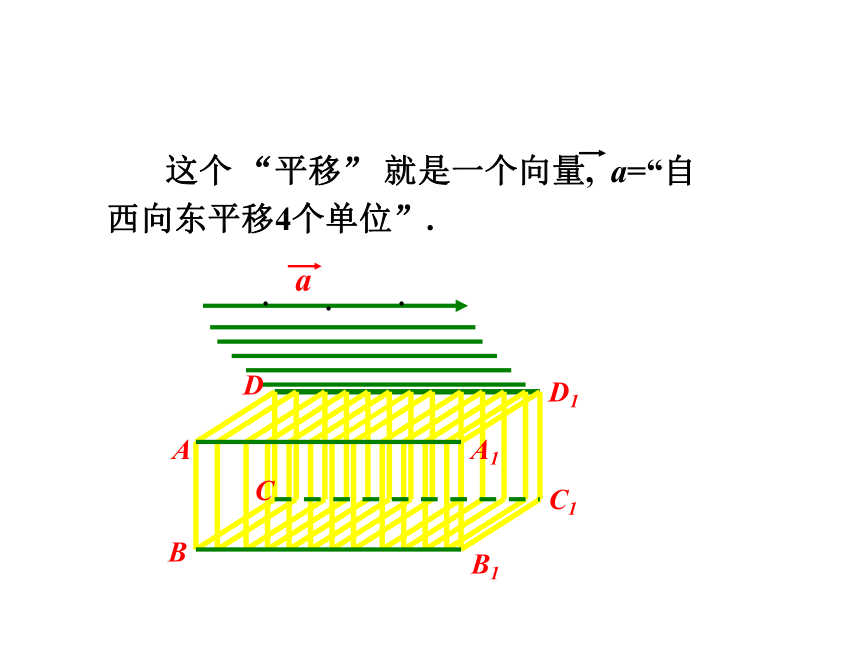
(1)空间的一个平移就是一个向量;
(2)向量一般用有向线段表示,同向等长的有向线段表示同一或相等的向量 ;
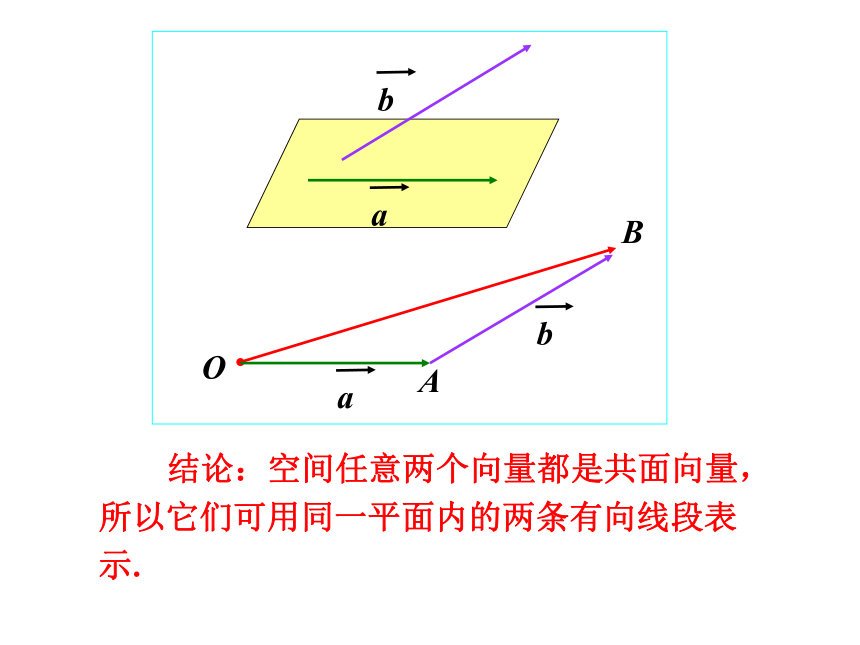
(3)空间的两个向量可用同一平面内的两条有向线段来表示.
结论:空间任意两个向量都是共面向量,所以它们可用同一平面内的两条有向线段表示.
1. 空间向量的加减运算
由于任意两个空间向量都能平移到同一空间,所以空间向量的加减运算与平面向量的加减运算相同.
加法: OB=OA+AB=a+b,
减法:CA=OA-OC=a-b.
2. 空间向量的加法运算律
(1)加法交换律
a + b = b + a
(2)加法结合律
(a + b) + c = a + (b + c)
你能证明下列性质吗?
证明加法交换律:
因为 OA = CB = a
AB = OC = b
所以 a + b = b + a
证明加法结合律:
因为 OC=OB+BC=(OA+AB)+BC=(a+b)+c
OC=OA+AC=OA+(AB+BC)=a+(b+c)
所以 (a + b) + c = a + (b + c)
1. 空间向量的运算就是平面向量运算的推广;
2. 两个向量相加的平行四边形法则在空间仍然成立;
3. 空间向量的加法运算可以推广至若干个向量相加.
3.对空间向量的加减法的说明
4.扩展
(1)首尾相接的若干向量之和,等于由起始向量的起点指向末尾向量的终点的向量.即:
(2)首尾相接的若干向量构成一个封闭图形,则它们的和为零向量.即:
已知平行六面体ABCD-A’B’C’D’,化简下列向量表达式,并标出化简结果的向量:
解答
(2)设M是线段CC’的中点,则
(4)设G是线段AC’靠近点A的三等分点,则
G
1.空间向量的概念.
在空间,具有大小和方向的量.
2.空间向量的加减运算.
空间向量的加减运算应用三角形法则和平行四边形法则.
3.空间向量的加法符合交换律,结合律.
4.平面向量与空间向量.
空间任意两个向量都可平移到同一个平面内,成为同一平面内的向量.
因此凡是涉及空间任意两个向量的问题,平面向量中有关结论仍适用于它们.
解析:
3.(2018年广东卷),D是△ABC的边AB上的中点,则向量CD=_____.
A
1.选择
平行六面体ABCD—A1B1C1D1中,M为AC和BD的交点,若 =a, =b, =c,则下列式子中与 相等的是( )
解答
故该题选 A
2.解答题
(1)在空间四边形ABCD中,点M、G分别是BC、CD边的中点,化简
解答
(2)已知平行六面体ABCD-A1B1C1D1,求满足下列各式的x的值.
复习平面向量
(1)什么是平面向量的定义?
(2)平面向量如何表示?
(3)什么是相等的向量?
(1)既有大小又有方向的量叫向量;
(2)向量有两种表示方法:
①几何表示法:用有向线段表示;
②字母表示法:用字母 等或者用有向线段的起点与终点字母AB表示.
(3)长度相等且方向相同的向量.
解答
平面向量的加减运算
看下面建筑
这个建筑钢架中有很多向量,但他们有些并不在同一平面内——这就是我们今天要学习的空间向量.
1. 空间向量
在空间,我们把具有大小和方向的量叫做空间向量(space vetor ).
向量的大小叫做向量的长度或模 (modulus).
2. 空间向量的表示
(1)我们规定,长度为0的向量叫做零向量(zero vector),记为0.当有向线段的起点A与终点B重合时,AB=0;
(2)模为1的向量称为单位向量(unit vector);
(3)两个向量不能比较大小,因为决定向量的两个因素是大小和方向,其中方向不能比较大小.
3. 相反向量
与向量 a 长度相等而方向相反的向量,称为 a 的相反向量,记为 – a .
4. 相等向量(equal vetor)
方向相同且模相等的向量称为相等向量.
(1)空间的一个平移就是一个向量;
(2)向量一般用有向线段表示,同向等长的有向线段表示同一或相等的向量 ;
(3)空间的两个向量可用同一平面内的两条有向线段来表示.
结论:空间任意两个向量都是共面向量,所以它们可用同一平面内的两条有向线段表示.
1. 空间向量的加减运算
由于任意两个空间向量都能平移到同一空间,所以空间向量的加减运算与平面向量的加减运算相同.
加法: OB=OA+AB=a+b,
减法:CA=OA-OC=a-b.
2. 空间向量的加法运算律
(1)加法交换律
a + b = b + a
(2)加法结合律
(a + b) + c = a + (b + c)
你能证明下列性质吗?
证明加法交换律:
因为 OA = CB = a
AB = OC = b
所以 a + b = b + a
证明加法结合律:
因为 OC=OB+BC=(OA+AB)+BC=(a+b)+c
OC=OA+AC=OA+(AB+BC)=a+(b+c)
所以 (a + b) + c = a + (b + c)
1. 空间向量的运算就是平面向量运算的推广;
2. 两个向量相加的平行四边形法则在空间仍然成立;
3. 空间向量的加法运算可以推广至若干个向量相加.
3.对空间向量的加减法的说明
4.扩展
(1)首尾相接的若干向量之和,等于由起始向量的起点指向末尾向量的终点的向量.即:
(2)首尾相接的若干向量构成一个封闭图形,则它们的和为零向量.即:
已知平行六面体ABCD-A’B’C’D’,化简下列向量表达式,并标出化简结果的向量:
解答
(2)设M是线段CC’的中点,则
(4)设G是线段AC’靠近点A的三等分点,则
G
1.空间向量的概念.
在空间,具有大小和方向的量.
2.空间向量的加减运算.
空间向量的加减运算应用三角形法则和平行四边形法则.
3.空间向量的加法符合交换律,结合律.
4.平面向量与空间向量.
空间任意两个向量都可平移到同一个平面内,成为同一平面内的向量.
因此凡是涉及空间任意两个向量的问题,平面向量中有关结论仍适用于它们.
解析:
3.(2018年广东卷),D是△ABC的边AB上的中点,则向量CD=_____.
A
1.选择
平行六面体ABCD—A1B1C1D1中,M为AC和BD的交点,若 =a, =b, =c,则下列式子中与 相等的是( )
解答
故该题选 A
2.解答题
(1)在空间四边形ABCD中,点M、G分别是BC、CD边的中点,化简
解答
(2)已知平行六面体ABCD-A1B1C1D1,求满足下列各式的x的值.
