人教版八年级数学下册第十八章 平行四边形 18.1 平行四边形 一课一练(含答案)
文档属性
| 名称 | 人教版八年级数学下册第十八章 平行四边形 18.1 平行四边形 一课一练(含答案) |  | |
| 格式 | zip | ||
| 文件大小 | 112.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-02-14 15:28:39 | ||
图片预览


文档简介
2020年人教版八年级数学下册
第十八章平行四边形一课一练
选择题
1、在四边形ABCD中,AD∥BC,若要使四边形ABCD是平行四边形,则应添加条件(??? )
A.∠A+∠C=180°????? B.∠B+∠D=180°????? C.∠A+∠B=180°?????? D.∠A+∠D=180°
2、如图,在四边形ABCD中,对角线AC、BD相交于点O,下列条件不能判定四边形ABCD为平行四边形的是(??? )
A.AB∥CD,AD∥BC????????????? B.OA=OC,OB=OD
C.AD=BC,AB∥CD?????????????? D.AB=CD,AD=BC
3、关于四边形:①两组对边分别平行;②两组对边分别相等;③两组对角相等;④对角线AC和BD相等.以上条件中,可以判定四边形是平行四边形的有: ?(? )
A.1个?????? B.2个??????? C.3个??????? D.4个
4、以长为3cm、4cm、6cm的三条线段中的两条为边,另一条为对角线画平行四边形,可以画出不同形状的平行四边形(? ).
A.1个??? ? B.2个????? C.3个? ???D.4个
5、下列性质中,平行四边形不一定具备的是()
A.对角互补 B.邻角互补 C.对角相等 D.内角和是360°
6、下面给出了四边形ABCD中∠A、∠B、∠C、∠D的度数之比,其中能判定四边形ABCD是平行四边形的是(??? )
A.1∶2∶2∶1????? B.2∶2∶1∶1?????? C.1∶2∶1∶2???? D.1∶1∶2∶2
7、如图,在平行四边形ABCD中,已知AD=5cm,AB=3cm,AE平分∠BAD交BC边于点E,则EC等于( ????)
A.1cm???? B.2cm???? ??? C.3cm???????? D.4cm
8、如图,平行四边形ABCD的周长是38cm,△ABC的周长是29cm,则AC的长为(??? )?
A.19cm B.13cm C.10cm D.9cm
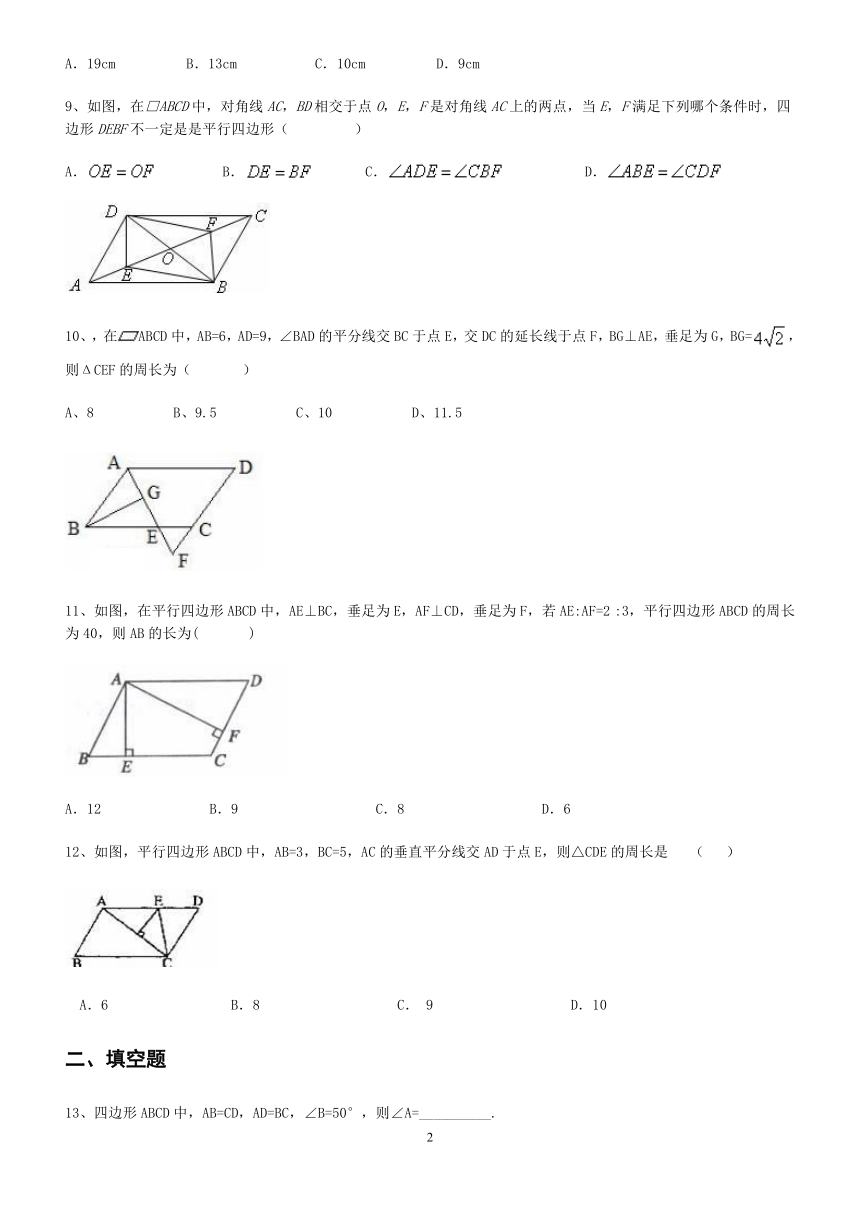
9、如图,在□ABCD中,对角线AC,BD相交于点O,E,F是对角线AC上的两点,当E,F满足下列哪个条件时,四边形DEBF不一定是是平行四边形(???? )
A.???? B. C.????? D.
10、,在ABCD中,AB=6,AD=9,∠BAD的平分线交BC于点E,交DC的延长线于点F,BG⊥AE,垂足为G,BG=,则ΔCEF的周长为(? ??)
A、8????? B、9.5????? C、10????? D、11.5
11、如图,在平行四边形ABCD中,AE⊥BC,垂足为E,AF⊥CD,垂足为F,若AE:AF=2 :3,平行四边形ABCD的周长为40,则AB的长为(??? )?
A.12??? ????B.9? ????????C.8??? ??????D.6
12、如图,平行四边形ABCD中,AB=3,BC=5,AC的垂直平分线交AD于点E,则△CDE的周长是? (? )
?A.6??? ?????B.8??? ??????C. 9??? ??????D.10
二、填空题
13、四边形ABCD中,AB=CD,AD=BC,∠B=50°,则∠A=__________.
14、?在四边形ABCD中,对角线AC,BD相交于点O,若要证明ABCD是平行四边形,则要证明OA=__________,OB=__________.
15、一个平行四边形的一条边长为3,两条对角线的长分别为4和2,则它的面积为__________.
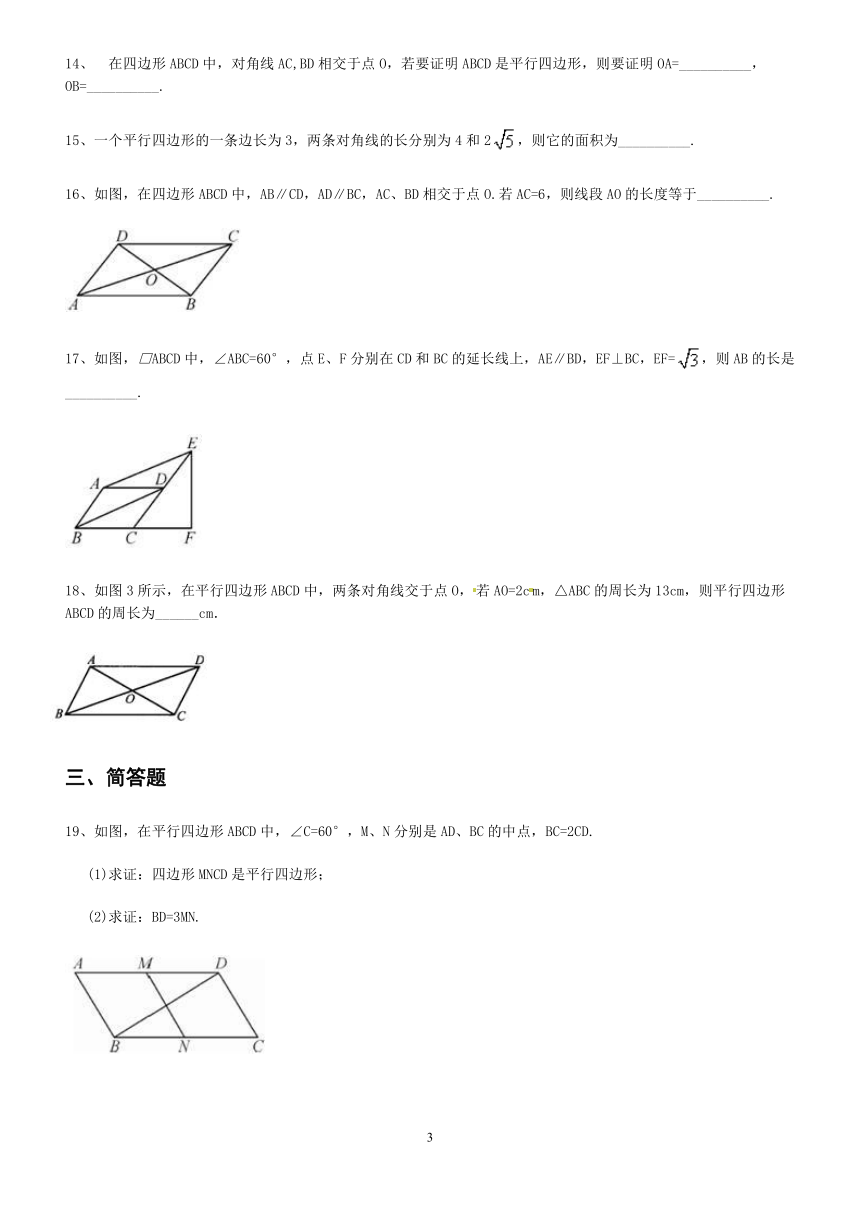
16、如图,在四边形ABCD中,AB∥CD,AD∥BC,AC、BD相交于点O.若AC=6,则线段AO的长度等于__________.
17、如图,□ABCD中,∠ABC=60°,点E、F分别在CD和BC的延长线上,AE∥BD,EF⊥BC,EF=,则AB的长是__________.
如图3所示,在平行四边形ABCD中,两条对角线交于点O,若AO=2cm,△ABC的周长为13cm,则平行四边形ABCD的周长为______cm.
三、简答题
19、如图,在平行四边形ABCD中,∠C=60°,M、N分别是AD、BC的中点,BC=2CD.
? (1)求证:四边形MNCD是平行四边形;
? (2)求证:BD=3MN.
20、如图,已知BE∥DF,∠ADF=∠CBE,AF=CE.求证:四边形DEBF是平行四边形.
??????????????????????????????????????????????????
21、已知:如图,在四边形ABCD中,AB∥CD,对角线AC、BD相交于点O,BO=DO.求证:四边形ABCD是平行四边形.
22、如图,在△ABC中,点D是BC边的中点,点F,E分别是AD及其延长线上的点,CF∥BE.
? (1)求证:△BDE≌△CDF.
? (2)请连接BF,CE,试证明四边形BECF是平行四边形.
23、如图,已知点O是□ABCD对角线AC的中点,过点O的直线EF分别交AB,CD于E,F两点.
(1)求证:四边形AECF是平行四边形;
(2)不添加辅助线,请写出图中所有全等的三角形(不需要证明).
参考答案
一、选择题
1、D;2、C;3、C;4、C;5、A;6、C;7、B;8、C;9、B;10、A;11、C;12、B;
二、填空题
13、130°?
14、OC? OD
15、4
16、3
17、1
18、18
三、简答题
19、证明:(1)∵ABCD是平行四边形,
∴AD=BC,AD∥BC.
∵M、N分别是AD、BC的中点,
∴MD=NC,MD∥NC.
∴MNCD是平行四边形;
? (2)连接ND,
∵MNCD是平行四边形,
∴MN=DC.
∵N是BC的中点,
∴BN=CN.
∵BC=2CD,∠C=60°,
∴△NCD是等边三角形.
∴ND=NC,∠DNC=60°.
∵∠DNC是△BND的外角,
∴∠NBD+∠NDB=∠DNC.
∵DN=NC=NB,
∴∠DBN=∠BDN=∠DNC=30°.
∴∠BDC=90°.
∴BC=2DC,BD===DC.
又DC=MN,∴BD=MN.
20、证明:∵BE∥DF,
∴∠AFD=∠CEB.
又∵∠ADF=∠CBE,AF=CE,
∴△ADF≌△CBE(AAS).
∴DF=BE.
又∵BE∥DF,
∴四边形DEBF是平行四边形.
21、证明:∵AB∥CD,
∴∠ABO=∠CDO,∠BAO=∠DCO.
又∵BO=DO,
∴△AOB≌△COD(AAS).
∴AB=CD.
∴四边形ABCD是平行四边形.
22、证明:(1)∵CF∥BE,
∴∠EBD=∠FCD.
又∵BD=CD,∠BDE=∠CDF,
∴△BDE≌△CDF(ASA).
? (2)证法1:由△BDE≌△CDF,得ED=FD.
又∵BD=CD,
∴四边形BECF是平行四边形(对角线互相平分的四边形是平行四边形).
? 证法2:由△BDE≌△CDF,得BE=CF,
又BE∥CF,
∴四边形BECF是平行四边形(一组对边平行且相等的四边形是平行四边形).
23、(1)证明:∵在□ABCD中,AB∥CD,
∴∠EAO=∠FCO.
又OA=OC,∠EOA=∠FOC,
∴△AOE≌△COF(ASA).
∴OE=OF,
又OA=OC.
∴四边形AECF为平行四边形.
? (2)△AOE≌△COF,△AOF≌△COE,△AFC≌△CEA,△AFE≌△CEF,△ADC≌△CBA,△ADF≌△CBE.
?
第十八章平行四边形一课一练
选择题
1、在四边形ABCD中,AD∥BC,若要使四边形ABCD是平行四边形,则应添加条件(??? )
A.∠A+∠C=180°????? B.∠B+∠D=180°????? C.∠A+∠B=180°?????? D.∠A+∠D=180°
2、如图,在四边形ABCD中,对角线AC、BD相交于点O,下列条件不能判定四边形ABCD为平行四边形的是(??? )
A.AB∥CD,AD∥BC????????????? B.OA=OC,OB=OD
C.AD=BC,AB∥CD?????????????? D.AB=CD,AD=BC
3、关于四边形:①两组对边分别平行;②两组对边分别相等;③两组对角相等;④对角线AC和BD相等.以上条件中,可以判定四边形是平行四边形的有: ?(? )
A.1个?????? B.2个??????? C.3个??????? D.4个
4、以长为3cm、4cm、6cm的三条线段中的两条为边,另一条为对角线画平行四边形,可以画出不同形状的平行四边形(? ).
A.1个??? ? B.2个????? C.3个? ???D.4个
5、下列性质中,平行四边形不一定具备的是()
A.对角互补 B.邻角互补 C.对角相等 D.内角和是360°
6、下面给出了四边形ABCD中∠A、∠B、∠C、∠D的度数之比,其中能判定四边形ABCD是平行四边形的是(??? )
A.1∶2∶2∶1????? B.2∶2∶1∶1?????? C.1∶2∶1∶2???? D.1∶1∶2∶2
7、如图,在平行四边形ABCD中,已知AD=5cm,AB=3cm,AE平分∠BAD交BC边于点E,则EC等于( ????)
A.1cm???? B.2cm???? ??? C.3cm???????? D.4cm
8、如图,平行四边形ABCD的周长是38cm,△ABC的周长是29cm,则AC的长为(??? )?
A.19cm B.13cm C.10cm D.9cm
9、如图,在□ABCD中,对角线AC,BD相交于点O,E,F是对角线AC上的两点,当E,F满足下列哪个条件时,四边形DEBF不一定是是平行四边形(???? )
A.???? B. C.????? D.
10、,在ABCD中,AB=6,AD=9,∠BAD的平分线交BC于点E,交DC的延长线于点F,BG⊥AE,垂足为G,BG=,则ΔCEF的周长为(? ??)
A、8????? B、9.5????? C、10????? D、11.5
11、如图,在平行四边形ABCD中,AE⊥BC,垂足为E,AF⊥CD,垂足为F,若AE:AF=2 :3,平行四边形ABCD的周长为40,则AB的长为(??? )?
A.12??? ????B.9? ????????C.8??? ??????D.6
12、如图,平行四边形ABCD中,AB=3,BC=5,AC的垂直平分线交AD于点E,则△CDE的周长是? (? )
?A.6??? ?????B.8??? ??????C. 9??? ??????D.10
二、填空题
13、四边形ABCD中,AB=CD,AD=BC,∠B=50°,则∠A=__________.
14、?在四边形ABCD中,对角线AC,BD相交于点O,若要证明ABCD是平行四边形,则要证明OA=__________,OB=__________.
15、一个平行四边形的一条边长为3,两条对角线的长分别为4和2,则它的面积为__________.
16、如图,在四边形ABCD中,AB∥CD,AD∥BC,AC、BD相交于点O.若AC=6,则线段AO的长度等于__________.
17、如图,□ABCD中,∠ABC=60°,点E、F分别在CD和BC的延长线上,AE∥BD,EF⊥BC,EF=,则AB的长是__________.
如图3所示,在平行四边形ABCD中,两条对角线交于点O,若AO=2cm,△ABC的周长为13cm,则平行四边形ABCD的周长为______cm.
三、简答题
19、如图,在平行四边形ABCD中,∠C=60°,M、N分别是AD、BC的中点,BC=2CD.
? (1)求证:四边形MNCD是平行四边形;
? (2)求证:BD=3MN.
20、如图,已知BE∥DF,∠ADF=∠CBE,AF=CE.求证:四边形DEBF是平行四边形.
??????????????????????????????????????????????????
21、已知:如图,在四边形ABCD中,AB∥CD,对角线AC、BD相交于点O,BO=DO.求证:四边形ABCD是平行四边形.
22、如图,在△ABC中,点D是BC边的中点,点F,E分别是AD及其延长线上的点,CF∥BE.
? (1)求证:△BDE≌△CDF.
? (2)请连接BF,CE,试证明四边形BECF是平行四边形.
23、如图,已知点O是□ABCD对角线AC的中点,过点O的直线EF分别交AB,CD于E,F两点.
(1)求证:四边形AECF是平行四边形;
(2)不添加辅助线,请写出图中所有全等的三角形(不需要证明).
参考答案
一、选择题
1、D;2、C;3、C;4、C;5、A;6、C;7、B;8、C;9、B;10、A;11、C;12、B;
二、填空题
13、130°?
14、OC? OD
15、4
16、3
17、1
18、18
三、简答题
19、证明:(1)∵ABCD是平行四边形,
∴AD=BC,AD∥BC.
∵M、N分别是AD、BC的中点,
∴MD=NC,MD∥NC.
∴MNCD是平行四边形;
? (2)连接ND,
∵MNCD是平行四边形,
∴MN=DC.
∵N是BC的中点,
∴BN=CN.
∵BC=2CD,∠C=60°,
∴△NCD是等边三角形.
∴ND=NC,∠DNC=60°.
∵∠DNC是△BND的外角,
∴∠NBD+∠NDB=∠DNC.
∵DN=NC=NB,
∴∠DBN=∠BDN=∠DNC=30°.
∴∠BDC=90°.
∴BC=2DC,BD===DC.
又DC=MN,∴BD=MN.
20、证明:∵BE∥DF,
∴∠AFD=∠CEB.
又∵∠ADF=∠CBE,AF=CE,
∴△ADF≌△CBE(AAS).
∴DF=BE.
又∵BE∥DF,
∴四边形DEBF是平行四边形.
21、证明:∵AB∥CD,
∴∠ABO=∠CDO,∠BAO=∠DCO.
又∵BO=DO,
∴△AOB≌△COD(AAS).
∴AB=CD.
∴四边形ABCD是平行四边形.
22、证明:(1)∵CF∥BE,
∴∠EBD=∠FCD.
又∵BD=CD,∠BDE=∠CDF,
∴△BDE≌△CDF(ASA).
? (2)证法1:由△BDE≌△CDF,得ED=FD.
又∵BD=CD,
∴四边形BECF是平行四边形(对角线互相平分的四边形是平行四边形).
? 证法2:由△BDE≌△CDF,得BE=CF,
又BE∥CF,
∴四边形BECF是平行四边形(一组对边平行且相等的四边形是平行四边形).
23、(1)证明:∵在□ABCD中,AB∥CD,
∴∠EAO=∠FCO.
又OA=OC,∠EOA=∠FOC,
∴△AOE≌△COF(ASA).
∴OE=OF,
又OA=OC.
∴四边形AECF为平行四边形.
? (2)△AOE≌△COF,△AOF≌△COE,△AFC≌△CEA,△AFE≌△CEF,△ADC≌△CBA,△ADF≌△CBE.
?
