华东师大版八年级数学上册第13章《全等三角形》单元综合测试(含答案)
文档属性
| 名称 | 华东师大版八年级数学上册第13章《全等三角形》单元综合测试(含答案) |

|
|
| 格式 | zip | ||
| 文件大小 | 237.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-02-14 00:00:00 | ||
图片预览


文档简介
第13章 全等三角形
一、填空题(每题2分,共20分)
1,所谓尺规作图中的尺规是指:___.
2,命题“垂直于同一条直线的两直线平行”的题设是_______,命题“平行于同一条直线的两直线平行”的结论是_________.
3,定理“如果直角三角形两直角边分别是a、b,斜边是c,那么a2+b2=c2.即直角三角形的两直角平方和等于斜边的平方”的逆定理是___.
4,如图1,根据SAS,如果AB=AC, = ,即可判定ΔABD≌ΔACE.
5,如图2,BD垂直平分线段AC,AE⊥BC,垂足为E,交BD于P点,PE=3cm,则P点到直线AB的距离是___.
6,如图3,在等腰Rt△ABC中,∠C=90°,AC=BC,AD平分∠BAC交BC于D,DE⊥AB于D,若AB=10,则△BDE的周长等于____.
7,如图4,△ABC≌△DEB,AB=DE,∠E=∠ABC,则∠C的对应角为 ,BD的对应边为 .
8,如图5,AD=AE,∠1=∠2,BD=CE,则有△ABD≌ ,理由是 ,△ABE≌△ ,理由是 .
9,若△ABC≌△DEF,其中A、B分别与D、E分别是对应的顶点,AB<AC<BC,则在△DEF中,________<_______<________.
10,如图6,AD⊥BC,DE⊥AB,DF⊥AC,D、E、F是垂足,BD=CD,那么图中的全等三角形有_______.
二、选择题(每题2分,共20分)
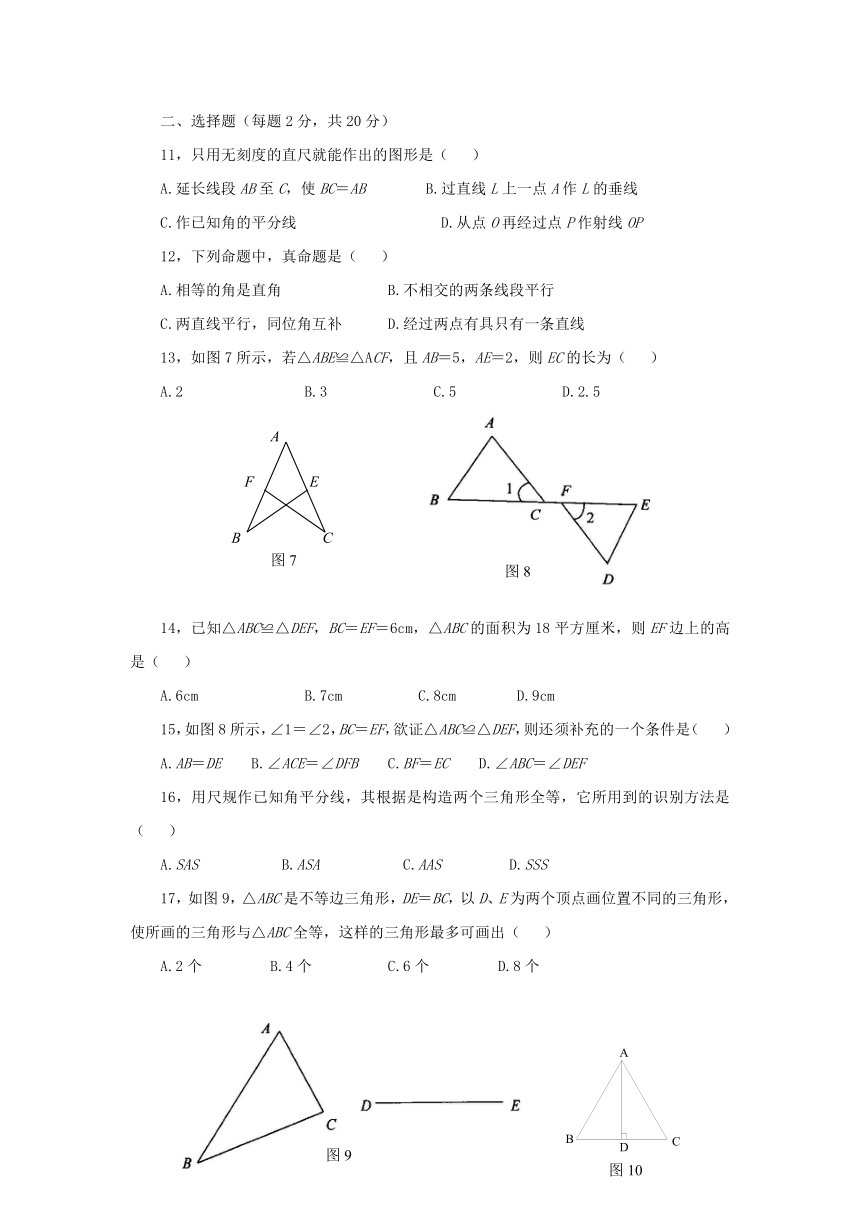
11,只用无刻度的直尺就能作出的图形是( )
A.延长线段AB至C,使BC=AB B.过直线L上一点A作L的垂线
C.作已知角的平分线 D.从点O再经过点P作射线OP
12,下列命题中,真命题是( )
A.相等的角是直角 B.不相交的两条线段平行
C.两直线平行,同位角互补 D.经过两点有具只有一条直线
13,如图7所示,若△ABE≌△ACF,且AB=5,AE=2,则EC的长为( )
A.2 B.3 C.5 D.2.5
14,已知△ABC≌△DEF,BC=EF=6cm,△ABC的面积为18平方厘米,则EF边上的高是( )
A.6cm B.7cm C.8cm D.9cm
15,如图8所示,∠1=∠2,BC=EF,欲证△ABC≌△DEF,则还须补充的一个条件是( )
A.AB=DE B.∠ACE=∠DFB C.BF=EC D.∠ABC=∠DEF
16,用尺规作已知角平分线,其根据是构造两个三角形全等,它所用到的识别方法是( )
A.SAS B.ASA C.AAS D.SSS
17,如图9,△ABC是不等边三角形,DE=BC,以D、E为两个顶点画位置不同的三角形,使所画的三角形与△ABC全等,这样的三角形最多可画出( )
A.2个 B.4个 C.6个 D.8个
18,如图10,△ABC中,AD⊥BC,D为BC中点,则以下结论不正确的是( )
A.△ABD≌△ACD B.∠B=∠C
C.AD是BAC的平分线 D.△ABC是等边三角形
19,如图11,∠1=∠2,∠C=∠D,AC、BD交于E点,下列结论中不正确的是( )
A.∠DAE=∠CBE B.CE=DE
C.△DEA不全等于△CBE D.△EAB是等腰三角形
20,如图12,在△ABC中,AB>AC,AC的垂直平分线交AB于点D,交AC于点E,AB=10,△BCD的周长为18,则BC的长为( )
A.8 B.6 C.4 D.2
三、解答题(共40分)
21,如图13,已知线段a、b,求作:Rt△ABC,使∠ACB=90?,BC=a,AC=b(不写作法,保留作图痕迹).
22,判断下列命题是真命题还是假命题,若是假命题,请举出一个反例说明.
(1)有一个角是60°的等腰三角形是等边三角形.
(2)有两个角是锐角的三角形是锐角三角形.
23,如图14,BP、CP是△ABC的外角平分线,则点P必在∠BAC的平分线上,你能说出其中的道理吗?
24,如图15,已知∠1=∠2,∠3=∠4,EC=AD,求证:AB=BE.
25,如图16,工人师傅制作了一个正方形窗架,把窗架立在墙上之前,在上面钉了两块等长的木条GF与GE,E、F分别是AD、BC的中点.
(1)G点一定是AB的中点吗?说明理由;
(2)钉这两块木条的作用是什么?
26,如图17,已知点A、E、F、D在同一条直线上,AE=DF,BF⊥AD,CE⊥AD,垂足分别为F、E,BF=CE,试说明AB与CD的位置关系.
四、综合题(共20分)
27,如图18,已知当物体AB距凸透镜为2倍焦距,即AO=2f时,成倒立的等大的像A′B′.求像距OA′与f的关系.
28,阅读下题及其证明过程:
已知:如图19,D是△ABC中BC边上一点,EB=EC,∠ABE=∠ACE,试说明∠BAE与∠CAE相等的理由.
理由:在△AEB和△AEC中,
所以△AEB≌△AEC(第一步)
所以∠BAE=∠CAE(第二步)
问:上面证明过程是否正确?若正确,请写出每一步推理根据;若不正确,请指出错在哪一步?并写出你认为正确的推理过程.
29,如图20,在四边形ABCD中,AD∥BC,∠ABC=∠DCB,AB=DC,AE=DF.
(1)试说明BF=CE的理由.
(2)当E、F相向运动,形成如图21时,BF和CE还相等吗?请说明你的结论和理由.
五、拓展题(共20分)
30,已知:如图22,AB=AC,DB=DC,
(1)若E、F、G、H分别是各边的中点,求证:EF=FG.
(2)若连结AD、BC交于点P,问AD、BC有何关系?证明你的结论.
31,如图23,在△AFD和△BEC中,点A、E、F、C在同一条直线上,有下面四个论断:(A)AD=CB,(B)AE=CF,(C)∠B=∠D,(D)AD∥BC.请用其中三个作为条件,余下一个作为结论,遍一道数学题,并写出解答过程.
32,我们知道,两边及其中一边的对角分别对应相等的两个三角形不一定全等.那么在什么情况下,它们会全等?
(1)阅读与说理:
对于这两个三角形均为直角三角形,显然它们全等.
对于这两个三角形均为钝角三角形,可证它们全等(证明略).
对于这两个三角形均为锐角三角形,它们也全等,可证明如下:
已知:如图24,△ABC、△A1B1C1均为锐角三角形,AB=A1B1,BC=B1Cl,∠C=∠Cl.试说明△ABC≌△A1B1C1的理由.
(请你将下列说理过程补充完整).
理由:分别过点B,B1作BD⊥CA于D,B1 D1⊥C1 A1于D1.则∠BDC=∠B1D1C1=90°,
因为BC=B1C1,∠C=∠C1,△BCD≌△B1C1D1,BD=B1D1.
(2)归纳与叙述:由(1)可得到一个正确结论,请你写出这个结论.
参考答案
一、1,没有刻度的直尺和圆规;2,两条直线垂直于同一条直线、两直线平行;3,如果三角形的三边长a、b、c满足a2+b2=c2,那么这个三角形就是直角三角形;4,AD=AE;5,3cm;6,10;7,∠DBE、CA;8,△ACE、SAS、△ACD、ASA(或SAS);9,DE、DF、EF;10,△ABD≌△ACD,△ADE≌△ADF,△BDE≌△CDF.
二、11,D;12,D;13,B;14,A;15,D;16,D;17,B;18,D;19,C;20,A.
三、21,略;22,(1)真命题,(2)假命题.例如:若在△ABC中,∠A=20°,∠B=30°,∠C=130°,则△ABC是钝角三角形;23,可过点P向三角形的三边引垂线,利用角平分线的性质即得;24,用AAS说明△ABD≌△EBC;25,(1)是.由HL知,AG=GB;(2)利用三角形的稳定性,使窗架稳定;26,AB∥CD.因为∠DBC=∠ACB,∠ABO=∠DCO,所以∠DBC+∠ABO=∠ACB+∠DCO,即∠ABC=∠DCB,又∠ACB=∠DBC,BC=CB,所以△ACB≌△DBC,所以AB=DC.因为∠ABO=∠DCO,∠AOB=∠DOC,所以△ABO≌△DCO,所以OA=OD.
四、27,在△AOB和△A′OB′中,因为AB=A′B′,∠BAO=∠B′A′O,∠BOA=∠B′OA′,所以△AOB≌△A′OB′,所以 OA′=OA,因为OA=2f,所以OA′=2f;
28,不正确,第一步就错.正确应该由EB=EC得到∠EBC=∠ECB,再由∠ABE=∠ACE,得∠ABC=∠ACB,即AB=AC,最后在△ABE和△ACE中,利用SAS得到△ABE≌△ACE即可说明∠BAE与∠CAE相等;29,(1)利用SAS说明△ABF≌△DCE,(2)相等.说明方法同(1).
五、30,(1)在△ABD和△ACD中,AB=AC,BD=CD,AD是公共边,所以△ABD≌△ACD(SSS),所以∠ABD=∠ACD,又BE=AB,CF=AC,所以BE=CF,同理 BH=CG ,所以△BEH≌△CFG (SAS),所以EH=FG ,(2)因为△ABD≌△ACD,所以∠BAD=∠CAD,因为AB=AC,所以AB垂直平分BC,即AD垂直平分BC;31,答案不惟一.如:已知:AE=CF,∠B=∠D,AD∥BC.求证:AD=BC.等等;32,(1)又因为AB=A1B1,∠ADB=∠A1D1B1=90°.所以△ADB≌△A1D1B1,所以∠A=∠A1,又∠C=∠C1,BC=B1C1,所以△ABC≌△A1B1C1.(2)由题设和(1)我们可以得到下列结论:若△ABC、△A1B1C1均为锐角三角形或均为直角三角形或均为钝角三角形,AB=A1B?1,BC=B1C1,∠C=∠C1,则△ABC≌△A1B1C1.
图3
E
D
C
B
A
图2
E
C
D
P
A
B
图1
E
D
C
B
A
E
D
A
B
C
1
2
图5
B
A
E
D
C
图4
图6
图8
图7
F
E
C
B
A
图10
图9
B
图11
A
图12
图14
A
P
B
C
图15
图13
b
a
图19
图17
图16
图18
图22
图23
A
B
C
D
E
F
图21
图20
图24
PAGE
