四年级上册数学单元测试-2.线和角 青岛版 (含答案)
文档属性
| 名称 | 四年级上册数学单元测试-2.线和角 青岛版 (含答案) |  | |
| 格式 | zip | ||
| 文件大小 | 101.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 青岛版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-02-14 20:42:23 | ||
图片预览

文档简介
四年级上册数学单元测试-2.线和角
一、单选题
1.两条直线相交,如果其中一个角是80°,那么和它相邻的角是(? )
A.?80°??????????????????????????????????????????B.?10°??????????????????????????????????????????C.?100°
2.如图线段AB、AC、AD、AE中最短的一条是(? )
A.?AB????????????????????????????????????????B.?AC????????????????????????????????????????C.?AD????????????????????????????????????????D.?AE
3.在图中,以下选项里最短的一条线段是(? )
A.?PA?????????????????????????????????????B.?PB?????????????????????????????????????C.?PC?????????????????????????????????????D.?PD?????????????????????????????????????E.?PE
二、判断题
4.连接两点的所有线中,线段最短。
5.两点之间线段最短.
6.两条平行直线间的距离线段最短.
三、填空题
7.两点之间的所有连线中,________最短。
8.在两山之间修隧道,是利用了________。
9.连接两点的线中,________最短.
四、解答题
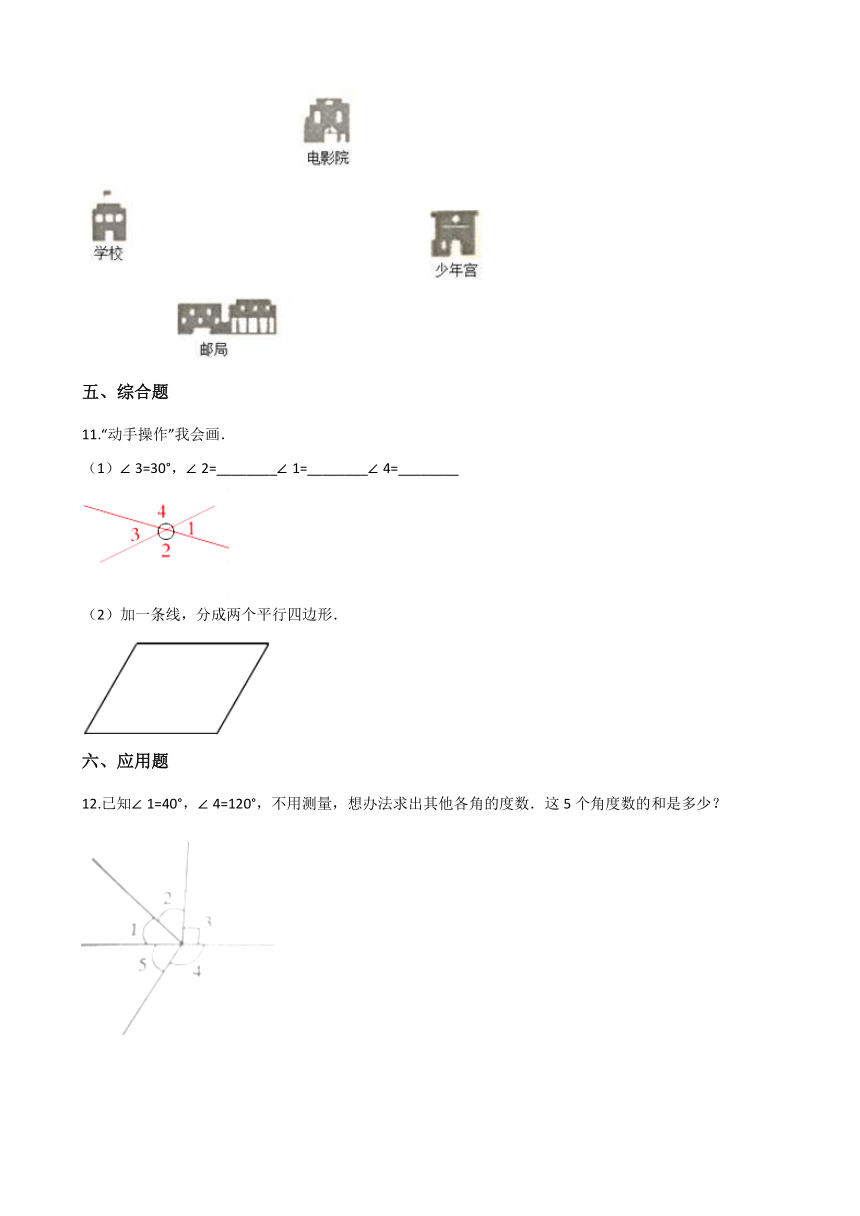
10.从学校到少年宫有几种走法,用“——”把路线画出来,并用“①、②、③”标出。哪条路线最近,请说明理由。
五、综合题
11.“动手操作”我会画.
(1)∠3=30°,∠2=________∠1=________∠4=________
(2)加一条线,分成两个平行四边形.
六、应用题
12.已知∠1=40°,∠4=120°,不用测量,想办法求出其他各角的度数.这5个角度数的和是多少?
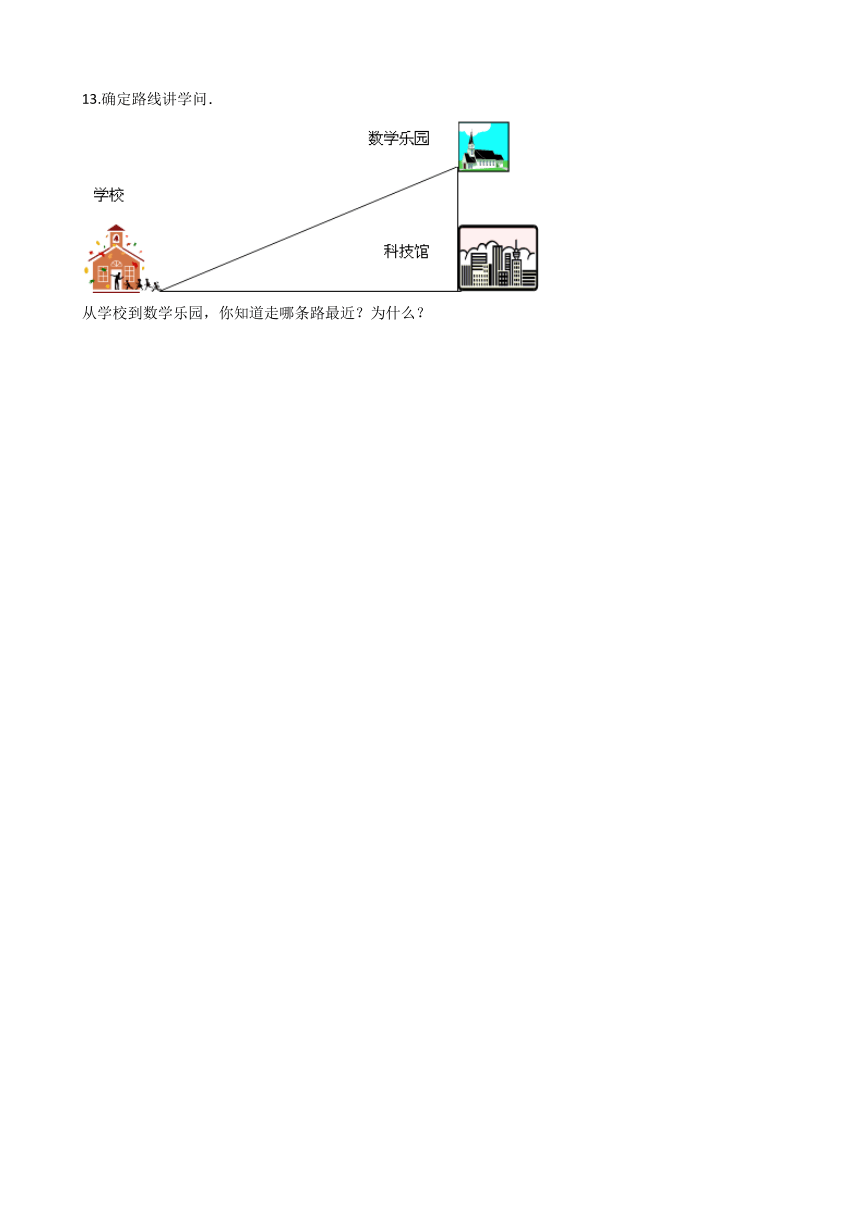
13.确定路线讲学问. 从学校到数学乐园,你知道走哪条路最近?为什么?
参考答案
一、单选题
1.【答案】 C
【解析】【解答】解:两条直线相交,如果其中一个角是80°,
那么和它相邻的角是:180°﹣80°=100°;
故选:C.
【分析】因为这个已知的角和它相邻的角组成一个平角,所以用180°减去80°即得.本题主要是利用平角的意义解决问题,关键是明确这个已知的角和它相邻的角组成一个平角.
2.【答案】 D
【解析】【解答】解:因为从A点向已知直线所作的垂线段最短,所以AE最短;
故选:D.
【分析】根据从直线外一点向直线所作的所有线段中,垂线段最短解答即可.此题主要考查垂线段的性质的灵活运用.
3.【答案】 C
【解析】【解答】解:因为从O点向已知直线所作的垂线段最短,所以PC最短.
故选:C.
【分析】根据从直线外一点向直线所作的所有线段中,垂线段最短解答即可.此题主要考查垂线段的性质的灵活运用.
二、判断题
4.【答案】正确
【解析】【解答】连接两点的所有线中,线段最短,此题说法正确. 故答案为:正确.
【分析】两点之间,线段最短,据此判断.
5.【答案】正确
【解析】【解答】解:由垂线段的性质可知:两点之间线段最短, 故答案为:正确. 【分析】根据垂线段的性质:两点之间线段最短,判断即可.本题考查了对垂线段的性质的掌握,熟练地记住垂线段的性质是解此题的关键.
6.【答案】错误
【解析】【解答】解:由分析可知,两条平行直线之间,只有垂线段最短, 所以题干说法错误, 故答案为:错误. 【分析】两条平行直线间可以画无数条线段,其中只有垂线段最短,据此即可判断.解答此题应明确:点到直线的距离,垂线段最短.
三、填空题
7.【答案】线段
【解析】【解答】解:两点之间的所有连线中,线段最短。 故答案为:线段【分析】两点之间有多种连线方法,其中线段是最短的。
8.【答案】两点之间线段最短。
【解析】【解答】解:在两山之间修隧道,是利用了两点之间线段最短。 故答案为:两点之间线段最短 【分析】两山可以看作是两个端点,两个端点之间线段是最短的,要想连接两点,挖出一条直的隧道是最短的。
9.【答案】线段
【解析】【解答】解:在连接两点的所有线中,最短的是线段; 故答案为:线段. 【分析】根据线段的性质:两点之间线段最短;即可得出答案.本题考查了线段的性质,属于基础题,注意对基本性质和概念的理解.
四、解答题
10.【答案】 解:从学校到少年宫有3种走法。 作图:
从学校直接到少年宫最近,因为两点之间线段最短。
【解析】【分析】①经过电影院到少年宫;②直接到少年宫;③经过邮局到少年宫。两点之间线段最短。
五、综合题
11.【答案】 (1)150°;30°;150° (2)解:由分析作图如下:
【解析】【解答】解:(1)根据平角是180°,得∠2=180°﹣30°=150°,依次可得:∠1=30°,∠4=150°.
故答案为:150°,30°,150°.
【分析】(1)根据平角是180°,则∠2=180°﹣30°,依次求出∠1、∠4即可.(2)根据平行四边形的对边平行且相等,只要在平行四边形的一条边上,从一个顶点量出一条线段,再在它的对边从它同侧的顶点量出同长的线段,然后边接这两个点即可.(1)考查平角是180°应用.(2)加的线段不只一条,有无数条,符合题意即可.
六、应用题
12.【答案】解:∠2=90°﹣40°=50° ∠3=90° ∠5=180°﹣120°=60° ∠1+∠2+∠3+∠4+∠5=40°+50°+90°+120°+60°=360° 答:∠2是50°,∠3是90°,∠5是60°,这5个角度数的和是360°
【解析】【分析】由题意可知:∠3是一个直角,则∠1和∠2构成了一个直角,所以可以求出∠2的度数;∠4和∠构成了一个平角,所以可以求出∠5的度数,据此即可求解.此题主要依据直角和平角的定义解决问题.
13.【答案】解:因为两点之间线段最短,所以从学校到数学乐园,选择直角三角形的斜边所在的路线最近
【解析】【分析】依据“两点之间线段最短”,即可选出正确的路线.此题考查了两点之间线段最短的知识.此题比较简单,解题的关键是注意数形结合思想的应用.
一、单选题
1.两条直线相交,如果其中一个角是80°,那么和它相邻的角是(? )
A.?80°??????????????????????????????????????????B.?10°??????????????????????????????????????????C.?100°
2.如图线段AB、AC、AD、AE中最短的一条是(? )
A.?AB????????????????????????????????????????B.?AC????????????????????????????????????????C.?AD????????????????????????????????????????D.?AE
3.在图中,以下选项里最短的一条线段是(? )
A.?PA?????????????????????????????????????B.?PB?????????????????????????????????????C.?PC?????????????????????????????????????D.?PD?????????????????????????????????????E.?PE
二、判断题
4.连接两点的所有线中,线段最短。
5.两点之间线段最短.
6.两条平行直线间的距离线段最短.
三、填空题
7.两点之间的所有连线中,________最短。
8.在两山之间修隧道,是利用了________。
9.连接两点的线中,________最短.
四、解答题
10.从学校到少年宫有几种走法,用“——”把路线画出来,并用“①、②、③”标出。哪条路线最近,请说明理由。
五、综合题
11.“动手操作”我会画.
(1)∠3=30°,∠2=________∠1=________∠4=________
(2)加一条线,分成两个平行四边形.
六、应用题
12.已知∠1=40°,∠4=120°,不用测量,想办法求出其他各角的度数.这5个角度数的和是多少?
13.确定路线讲学问. 从学校到数学乐园,你知道走哪条路最近?为什么?
参考答案
一、单选题
1.【答案】 C
【解析】【解答】解:两条直线相交,如果其中一个角是80°,
那么和它相邻的角是:180°﹣80°=100°;
故选:C.
【分析】因为这个已知的角和它相邻的角组成一个平角,所以用180°减去80°即得.本题主要是利用平角的意义解决问题,关键是明确这个已知的角和它相邻的角组成一个平角.
2.【答案】 D
【解析】【解答】解:因为从A点向已知直线所作的垂线段最短,所以AE最短;
故选:D.
【分析】根据从直线外一点向直线所作的所有线段中,垂线段最短解答即可.此题主要考查垂线段的性质的灵活运用.
3.【答案】 C
【解析】【解答】解:因为从O点向已知直线所作的垂线段最短,所以PC最短.
故选:C.
【分析】根据从直线外一点向直线所作的所有线段中,垂线段最短解答即可.此题主要考查垂线段的性质的灵活运用.
二、判断题
4.【答案】正确
【解析】【解答】连接两点的所有线中,线段最短,此题说法正确. 故答案为:正确.
【分析】两点之间,线段最短,据此判断.
5.【答案】正确
【解析】【解答】解:由垂线段的性质可知:两点之间线段最短, 故答案为:正确. 【分析】根据垂线段的性质:两点之间线段最短,判断即可.本题考查了对垂线段的性质的掌握,熟练地记住垂线段的性质是解此题的关键.
6.【答案】错误
【解析】【解答】解:由分析可知,两条平行直线之间,只有垂线段最短, 所以题干说法错误, 故答案为:错误. 【分析】两条平行直线间可以画无数条线段,其中只有垂线段最短,据此即可判断.解答此题应明确:点到直线的距离,垂线段最短.
三、填空题
7.【答案】线段
【解析】【解答】解:两点之间的所有连线中,线段最短。 故答案为:线段【分析】两点之间有多种连线方法,其中线段是最短的。
8.【答案】两点之间线段最短。
【解析】【解答】解:在两山之间修隧道,是利用了两点之间线段最短。 故答案为:两点之间线段最短 【分析】两山可以看作是两个端点,两个端点之间线段是最短的,要想连接两点,挖出一条直的隧道是最短的。
9.【答案】线段
【解析】【解答】解:在连接两点的所有线中,最短的是线段; 故答案为:线段. 【分析】根据线段的性质:两点之间线段最短;即可得出答案.本题考查了线段的性质,属于基础题,注意对基本性质和概念的理解.
四、解答题
10.【答案】 解:从学校到少年宫有3种走法。 作图:
从学校直接到少年宫最近,因为两点之间线段最短。
【解析】【分析】①经过电影院到少年宫;②直接到少年宫;③经过邮局到少年宫。两点之间线段最短。
五、综合题
11.【答案】 (1)150°;30°;150° (2)解:由分析作图如下:
【解析】【解答】解:(1)根据平角是180°,得∠2=180°﹣30°=150°,依次可得:∠1=30°,∠4=150°.
故答案为:150°,30°,150°.
【分析】(1)根据平角是180°,则∠2=180°﹣30°,依次求出∠1、∠4即可.(2)根据平行四边形的对边平行且相等,只要在平行四边形的一条边上,从一个顶点量出一条线段,再在它的对边从它同侧的顶点量出同长的线段,然后边接这两个点即可.(1)考查平角是180°应用.(2)加的线段不只一条,有无数条,符合题意即可.
六、应用题
12.【答案】解:∠2=90°﹣40°=50° ∠3=90° ∠5=180°﹣120°=60° ∠1+∠2+∠3+∠4+∠5=40°+50°+90°+120°+60°=360° 答:∠2是50°,∠3是90°,∠5是60°,这5个角度数的和是360°
【解析】【分析】由题意可知:∠3是一个直角,则∠1和∠2构成了一个直角,所以可以求出∠2的度数;∠4和∠构成了一个平角,所以可以求出∠5的度数,据此即可求解.此题主要依据直角和平角的定义解决问题.
13.【答案】解:因为两点之间线段最短,所以从学校到数学乐园,选择直角三角形的斜边所在的路线最近
【解析】【分析】依据“两点之间线段最短”,即可选出正确的路线.此题考查了两点之间线段最短的知识.此题比较简单,解题的关键是注意数形结合思想的应用.
