2020年湘教版数学九年级下册第一章《二次函数》综合卷(含答案)
文档属性
| 名称 | 2020年湘教版数学九年级下册第一章《二次函数》综合卷(含答案) |

|
|
| 格式 | zip | ||
| 文件大小 | 157.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 湘教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-02-14 00:00:00 | ||
图片预览


文档简介
2020年湘教版数学九年级下册
第一章《二次函数》综合卷
一、选择题
1.下列函数中,是二次函数的为(?? )
A.?????????????????B.?????????????????C.?????????????????D.?
2.二次函数y=2x2﹣3的二次项系数、一次项系数和常数项分別是(?? )
A.?2、0、﹣3??????????????????????????B.?2、﹣3、0??????????????????????????C.?2、3、0??????????????????????????D.?2、0、3
3.函数 的图象与坐标轴的交点个数是(???? )
A.?0?????????????????????????????????????????B.?? 1?????????????????????????????????????????C.?? 2?????????????????????????????????????????D.?? 3
4.抛物线 经变换后得到抛物线 ,则这个变换可以是(???? )
A.?向左平移2个单位???????????B.?向右平移2个单位???????????C.?向左平移5个单位???????????D.?向右平移5个单位
5.将抛物线 向左平移2个单位长度,再向下平移3个单位长度,得到的抛物线的解析式为:(?? )
A.???????????????B.???????????????C.???????????????D.?
6.二次函数的部分图象如图所示,对称轴是x=﹣1,则这个二次函数的表达式为(?? )
A.?y=﹣x2+2x+3?????????????????B.?y=x2+2x+3???????????????? C.?y=﹣x2﹣2x+3?????????????????D.?y=﹣x2+2x﹣3
7.若二次函数y=ax2的图象经过点p(-2 , 4),则该图象必经过点(?? )
A.?(2, 4)??????????????????????????B.?(-2,? - 4)??????????????????????????C.?(- 4, 2)??????????????????????????D.?(4, -2)
8.已知二次函数y=ax2+4x+c , 当x等于﹣2时,函数值是﹣1;当x=1时,函数值是5.则此二次函数的表达式为( ??)
A.?y=2x2+4x﹣1????????????????B.?y=x2+4x﹣2????????????????C.?y=﹣2x2+4x+1????????????????D.?y=2x2+4x+1
9.当﹣2≤x≤1时,二次函数y=﹣(x﹣m)2+m2+1有最大值4,则实数m的值为(?? )
A.???????????????????????B.?或 ??????????????????????C.?2或 ??????????????????????D.?2或 或
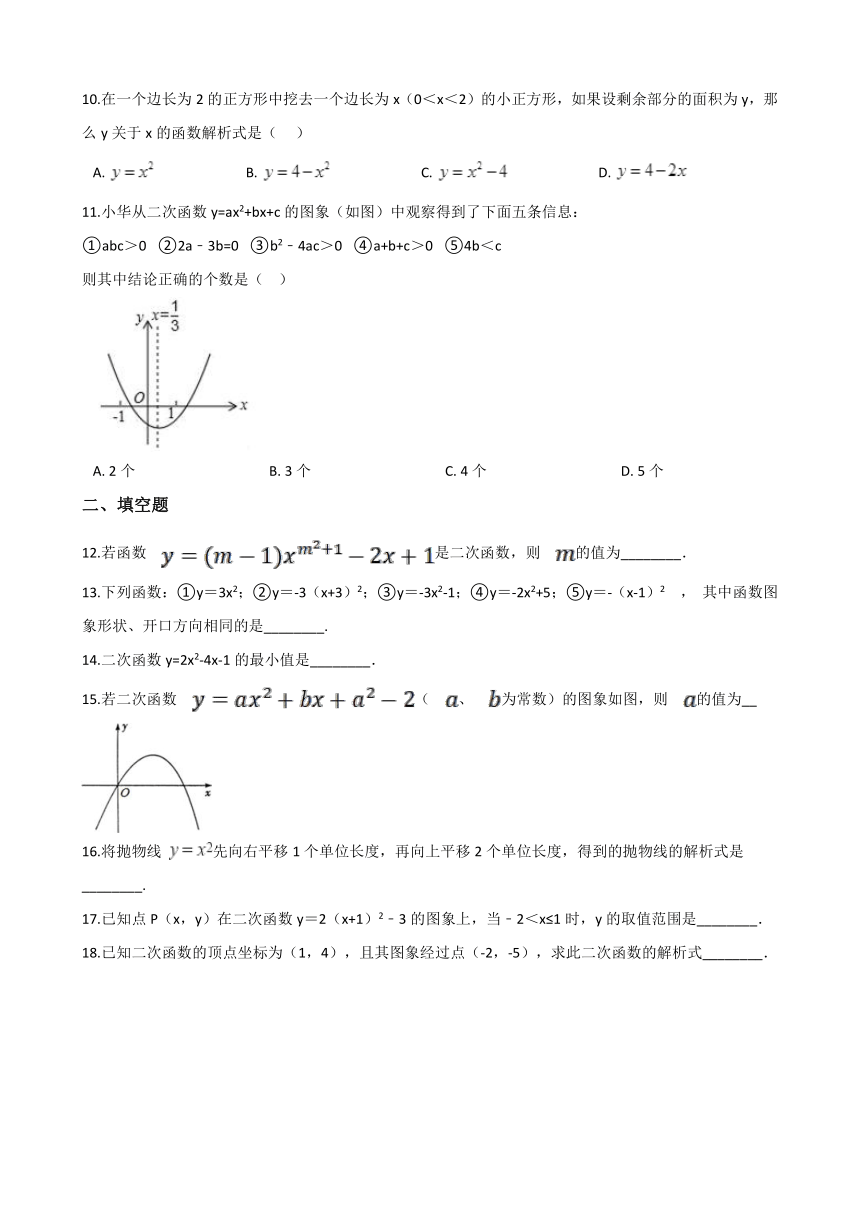
10.在一个边长为2的正方形中挖去一个边长为x(0<x<2)的小正方形,如果设剩余部分的面积为y,那么y关于x的函数解析式是(??? )
A.???????????????????????????B.???????????????????????????C.???????????????????????????D.?
11.小华从二次函数y=ax2+bx+c的图象(如图)中观察得到了下面五条信息:
①abc>0? ②2a﹣3b=0? ③b2﹣4ac>0? ④a+b+c>0? ⑤4b<c
则其中结论正确的个数是(?? )
A.?2个???????????????????????????????????????B.?3个???????????????????????????????????????C.?4个???????????????????????????????????????D.?5个
二、填空题
12.若函数 是二次函数,则 的值为________.
13.下列函数:①y=3x2;②y=-3(x+3)2;③y=-3x2-1;④y=-2x2+5;⑤y=-(x-1)2 , 其中函数图象形状、开口方向相同的是________.
14.二次函数y=2x2-4x-1的最小值是________.
15.若二次函数 ( 、 为常数)的图象如图,则 的值为__
16.将抛物线 先向右平移1个单位长度,再向上平移2个单位长度,得到的抛物线的解析式是________.
17.已知点P(x,y)在二次函数y=2(x+1)2﹣3的图象上,当﹣2<x≤1时,y的取值范围是________.
18.已知二次函数的顶点坐标为(1,4),且其图象经过点(-2,-5),求此二次函数的解析式________.
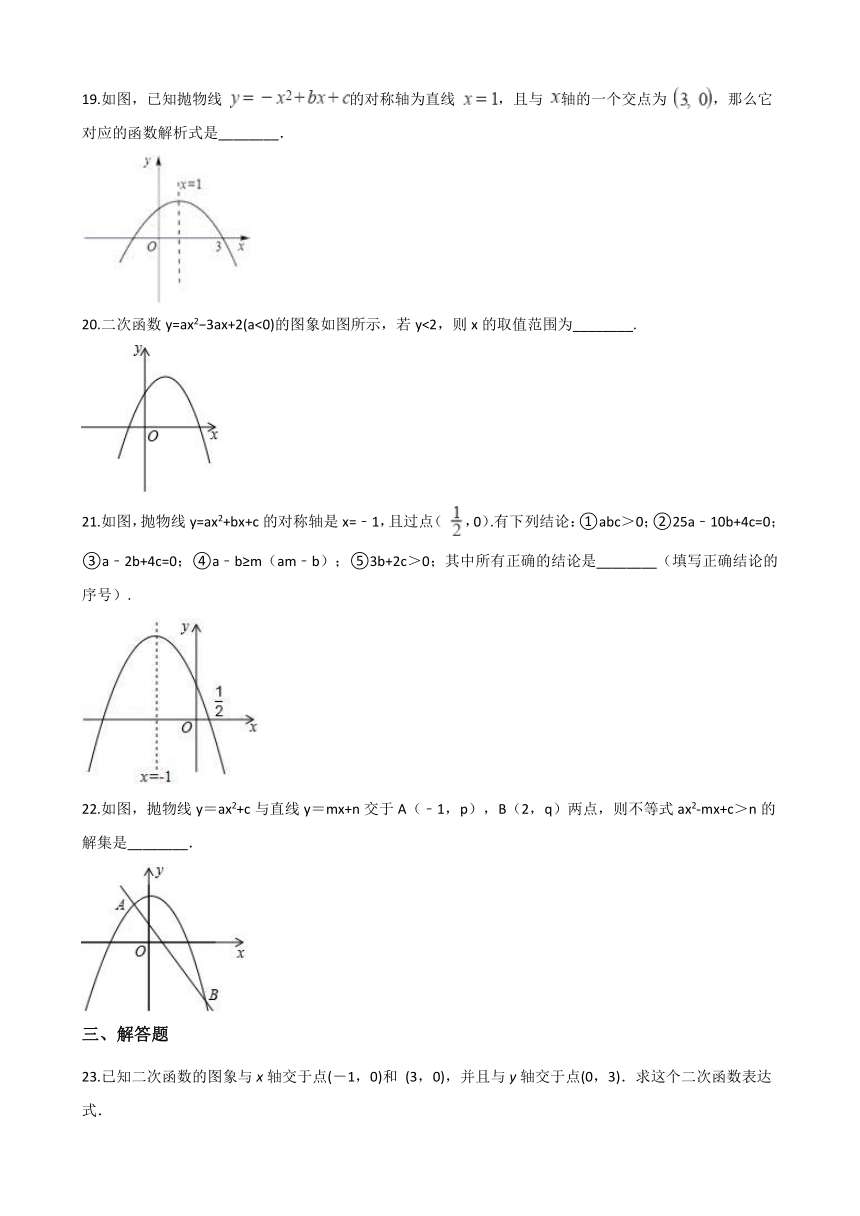
19.如图,已知抛物线 的对称轴为直线 ,且与 轴的一个交点为 ,那么它对应的函数解析式是________.
20.二次函数y=ax2?3ax+2(a<0)的图象如图所示,若y<2,则x的取值范围为________.
21.如图,抛物线y=ax2+bx+c的对称轴是x=﹣1,且过点( ,0).有下列结论:①abc>0;②25a﹣10b+4c=0;③a﹣2b+4c=0;④a﹣b≥m(am﹣b);⑤3b+2c>0;其中所有正确的结论是________(填写正确结论的序号).
22.如图,抛物线y=ax2+c与直线y=mx+n交于A(﹣1,p),B(2,q)两点,则不等式ax2-mx+c>n的解集是________.
三、解答题
23.已知二次函数的图象与x轴交于点(-1,0)和 (3,0),并且与y轴交于点(0,3).求这个二次函数表达式.
24.抛物线y=x2-(m+1)x+m与y轴交于(0,-3)点。
(1)求出m的值和抛物线与x轴的交点;
(2)x取什么值时,y>0?
25.小李家用 长的篱笆围成一个一边靠墙(墙足够长)的矩形菜园,如图.
(1)写出这块菜园的面积 与垂直于墙的边长 之间的函数解析式;
直接写出 的取值范围.
26.如图A(﹣4,0),C(0,3),将线段CA以点C为旋转中心旋转,所得的对应线段记为CA',当点A'落在y轴上时,写出A'的坐标,并求出以A'为顶点,经过A(﹣4,0)的抛物线的解析式.
27.已知抛物线 经过坐标原点O,与x轴交于另一点A,顶点为B.求:
(1)抛物线的解析式;
(2)△AOB的面积;
(3)要使二次函数的图象过点(10,0),应把图象沿x轴向右平移________个单位
28.在平面直角坐标系xOy中,抛物线y=ax2﹣2x(a≠0)与x轴交于点A , B(点A在点B的左侧)
(1)当a=﹣1时,求A , B两点的坐标;
(2)过点P(3,0)作垂直于x轴的直线l , 交抛物线于点C . 当a=2时,求PB+PC的值.
参考答案
一、选择题
1. D 2. A 3. B 4. B 5. B 6. C 7. B 8. A 9. C 10. B 11. B
二、填空题
12. 13. ②③ 14. -3 15. - 16. 17. ﹣3≤y≤5
18. y=-(x-1)2+4 19. 20. x<0或x>3 21. ①②④ 22. ﹣1<x<2
三、解答题
23. 解:设二次函数的表达式为 ,
把点(-1,0), (3,0)和(0,3)代入,则
,
解得: ,
∴二次函数的表达式为: .
24. (1)解:把(0,-3)代入y=x2-(m+1)x+m,得m=-3
令y=0,得0=x2+2x-3,解得x1=-3,x2=1
∴抛物线与x轴的交点为(-3,0)和(1,0)
(2)解:∵抛物线开口向上,∴当x<-3或x>1时,y>0
25. 解:∵垂直于墙的边长为 ,
∴平行于墙的边长为 ,
∴ ,
即 与 之间的函数关系式为
直接写出 的取值范围.
解:由题意,得 ,
解得
26.解:∵A(﹣4,0),C(0,3), ∴AC= =5.①当将线段CA以点C为旋转中心,顺时针旋转时,A′(0,8).
设该函数解析式为y=ax2+8.
把A(﹣4,0)代入得到:0=16a+8,
解得a=﹣ .
故该函数解析式为:y=﹣ x2+8.②当将线段CA以点C为旋转中心,逆时针旋转时,A′(0,2).
设该函数解析式为y=ax2﹣2.
把A(﹣4,0)代入得到:0=16a﹣2,
解得a= .
故该函数解析式为:y= x2+2.
综上所述,该二次函数解析式为:y=﹣ x2+8或y= x2+2
27. (1)解: ∵抛物线 经过坐标原点O
∴n+1=0,n=﹣1,
∴抛物线解析式为:
(2)解: ,∴顶点B的坐标(2,-4);
抛物线 与x轴交点为(4,0)(0,0)
∴点A的坐标(4,0)??
所以△AOB的面积是
(3)图象沿x轴向右平移6或10 个单位.
28. (1)解:当a=﹣1时,有y=﹣x2﹣2x.
令y=0,得:﹣x2﹣2x=0.
解得x1=0,x2=﹣2.
∵点A在点B的左侧,
∴A(﹣2,0),B(0,0);
(2)解:当a=2时,有y=2x2﹣2x.
令y=0,得2x2﹣2x=0.
解得x1=0,x2=1.
∵点A在点B的左侧,
∴A(0,0),B(1,0).
∴PB=2,
当x=3时, ,
∴PC=12.
∴PB+PC=14.
