人教版数学七年级下册第八章:8.2二元一次方程组的定义及解法学案(含答案)
文档属性
| 名称 | 人教版数学七年级下册第八章:8.2二元一次方程组的定义及解法学案(含答案) |
|
|
| 格式 | zip | ||
| 文件大小 | 3.3MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-02-14 00:00:00 | ||
图片预览





文档简介
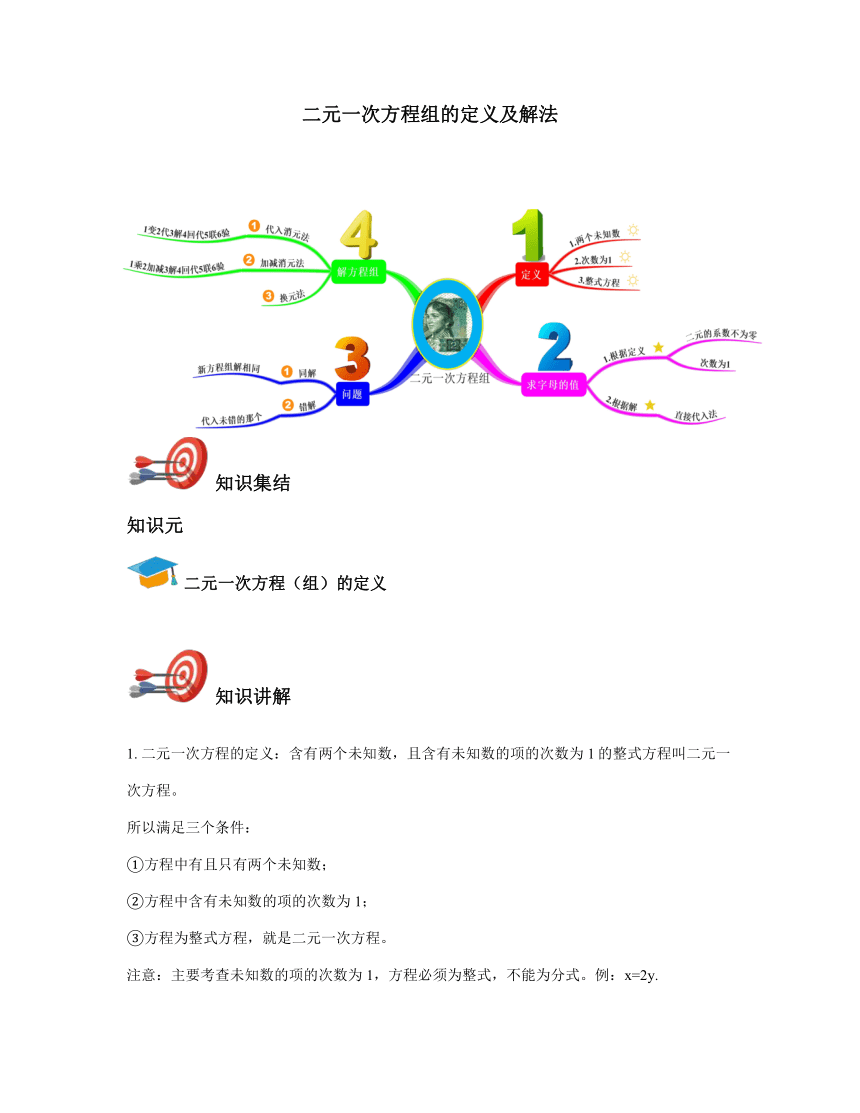
二元一次方程组的定义及解法
知识集结
知识元
二元一次方程(组)的定义
知识讲解
1. 二元一次方程的定义:含有两个未知数,且含有未知数的项的次数为1的整式方程叫二元一次方程。
所以满足三个条件:
①方程中有且只有两个未知数;
②方程中含有未知数的项的次数为1;
③方程为整式方程,就是二元一次方程。
注意:主要考查未知数的项的次数为1,方程必须为整式,不能为分式。例:x=2y.
2.二元一次方程组的定义:由几个一次方程组成并且含有两个未知数的方程组,叫二元一次方程组。
注意三条:
①方程组中有且只有两个未知数。
②方程组中含有未知数的项的次数为1。?
③方程组中每个方程均为整式方程。
注意:二元一次方程组不一定由两个二元一次方程合在一起:
①方程可以超过两个;
②有的方程可以只有一元。
例题精讲
二元一次方程(组)的定义
例1.
下列方程中,是二元一次方程的是( ).
A.8x2+1=y B.y=8x+1
C.y= D.xy=1
【答案】B
【解析】
题干解析:
二元一次方程必须符合以下三个条件:方程中只含有2个未知数;含未知数项的最高次数为一次;方程是整式方程.
根据二元一次方程的定义求解即可.
A、是一元二次方程,故A不符合题意;
B、是二元一次方程,故B符合题意;
C、是分式方程,故C不符合题意;
D、是二元二次方程,故D不符合题意;故选:B.
例2.
下列方程组中,是二元一次方程组的是( ).
A. B. C. D.
【答案】C
【解析】
题干解析:
考查二元一次方程组的定义:由几个一次方程组成并且含有两个未知数的方程组,叫二元一次方程组。
注意三条:
①方程组中有且只有两个未知数。
②方程组中含有未知数的项的次数为1。
③方程组中每个方程均为整式方程。
A、该方程中的第一个方程是分式方程,故本选项错误;
B、该方程组中含有3个未知数,属于三元一次方程组,故本选项错误;
C、该方程组符合二元一次方程组的定义,故本选项正确;
D、该方程组属于二元二次方程组,故本选项错误;故选:C.
例3.
有下列方程组:(1) (2) (3) (4),其中说法正确的是( ).
A.只有(1)、(3)是二元一次方程组
B.只有(3)、(4)是二元一次方程组
C.只有(4)是二元一次方程组
D.只有(2)不是二元一次方程组
【答案】D
【解析】
题干解析:
考查二元一次方程组的定义:由几个一次方程组成并且含有两个未知数的方程组,叫二元一次方程组。
只有(2)不是二元一次方程组,其中未知数的项的次数为2,不为1.其余的都符合二元一次方程组的定义。
根据定义求字母的值
知识讲解
含有参数的二元一次方程组,根据二元一次方程的定义:
1.二元的系数不为零。
2.未知数的次数为1。
注意:出现在选择填空题时,可以不用解出方程,可以直接将m,n的值代入验证即可。
?
例题精讲
根据定义求字母的值
例1.
已知3 =y是二元一次方程,那么k的值是( ).
A.2 B.3 C.1 D.0
【答案】C
【解析】
题干解析:
∵3x2﹣k=y是二元一次方程,
∴未知数项的最高次数为一次,
∴2﹣k=1,
解得k=1.故选C.
例2.
若﹣8 =10是关于x,y的二元一次方程,则m+n= .
【答案】
2
【解析】
题干解析:由题意得:m﹣2=1,n+2=1,解得:m=3,n=﹣1,m+n=2.
例3.
若(a-3)x+=9是关于x,y的二元一次方程,求a的值。
【答案】
-3
【解析】
题干解析:解:由题意得:解得:a=-3
根据二元一次方程(组)的解确定字母的值
知识讲解
当一组数对为二元一次方程(组)的解时,即,将这组数对代入方程(组)中能满足所有方程等式成立。
注意:遇到选择题时,直接用代入法求出其它字母的值即可。
?
例题精讲
根据二元一次方程(组)的解确定字母的值
例1.
方程组的解满足x+y=0,则m=______。
【答案】
-5
【解析】
题干解析:将x=-y带入方程组,得到解得
例2.
若关于x,y的方程组与有相同的解.
(1)求这个相同的解;
(2)求m,n的值。
【答案】
见解析
【解析】
题干解析:解:(1)联立得:,解得:;(2)把x=2,y=﹣1代入得:,解得:m=6,n=4。
例3.
已知二元一次方程组则m + n的值是( ).
A.1 B.0 C.-2 D.-1
【答案】D
【解析】
题干解析:
(1)-(2)得:-m-n=1
所以m + n=-1
例4.
已知方程组中的x ,y相等,则n的值为( ).
A.1 B.3 C.-3 D.-4
【答案】D
【解析】
题干解析:
因为 中的x ,y相等,
所以原方程组可化为
由①得:y=
把y= 代入②得 =n+1,
解得n=-4。
例5.
方程组的解为,则被遮盖的两个数分别为( ).
A.5,1 B.1,3 C.2,3 D.2,4
【答案】A
【解析】
题干解析:
解:根据题意,得2+y=3,
解,得y=1.
则2x+y=4+1=5.
则第一个被遮盖的数是5,第二个被遮盖的数是1.
用代入消元法和加减消元法解方程组
知识讲解
代入消元法步骤:1变,2代,3解,4回代,5联,6验
移项时要注意符号要改变。
加减消元法步骤:1乘,2加减,3解,4回代,5联,6验
注意:将未知数系数变为相同时,需要方程左右两边都乘除同一个不为零的数。
例题精讲
用代入消元法和加减消元法解方程组
例1.
二元一次方程组的解为( )
A. B. C. D.
【答案】B
【解析】
题干解析:
解:两方程相加可得:x=2
把x=2代入2x-y=0可得:y=4
故方程组的解为:
例2.
用代入消元法求解下列方程组.
(1)
(2)
(3)
【答案】
见解析
【解析】
题干解析:(1)先把方程组化简再求解.解法(1):由原方程组得把①代入②得2(6y﹣1)﹣y=9,即y=1;代入①得:x=5;∴原方程组的解为.解法(2):由得:x+1=6y,把①代入2(x+1)﹣y=11得:12y﹣y=11,即y=1;把y=1代入①得:x=5;∴原方程组的解为.(2),由②得:x=﹣3y+1③,把③代入①得:﹣9y+3﹣2y=﹣1,移项合并得:11y=4,解得:y=,把y=代入③得:x=﹣,则方程组的解为;(3)先把方程②去分母进行化简,再把方程①写成x=7+2y的形式,然后利用代入消元法求解.解:化简方程组,得,把x=2y+7代入6x+y=3得:y=﹣3,代入x=2y+7得:x=1.故原方程组的解是:
例3.
用加减消元法解下列二元一次方程组。
(1)
(2)
(3)
【答案】
见解析
【解析】
题干解析:(1)由于方程组中两方程y的系数是倍数关系,且数值较小,故可先用加减消元法再用代入消元法求解.解:,②×2+①得,7x﹣14=0,解得x=2;把x=2代入②得,2+y﹣5=0,解得y=3.故原方程组的解为:.(2) ,①+②得:5x=5,即x=1,把x=1代入①得:y=﹣3,则方程组的解为.(3),①×4+②×3得:37x=111,即x=3,把x=3代入①得:y=﹣9,则方程组的解为.
例4.
解方程组:
【答案】
见解析
【解析】
题干解析:解:方程组整理得:,①+②得:8x=24,解得:x=3,把x=3代入②得:y=﹣5,则方程组的解为。
用换元法解二元一次方程(组)
知识讲解
当原方程(组)特别复杂或者未知数指数为-1时,可以用换元法解题。
例题精讲
用换元法解二元一次方程(组)
例1.
若关于 x,y的方程组 (其中 a,b 是常数)的解为 则方程组 的解为 ( ).
A. B. C. D.
【答案】B
【解析】
题干解析:
因为方程组 的解为
所以方程组 的解为
解得
例2.
解方程组 .
【答案】
【解析】
题干解析:方法①:方程组整理得:,①×3+②得:﹣35x=37,即x=﹣,把x=﹣代入②得:y=,则方程组的解为.方法②:令m=x-2y,n=5x-3y.则①; ②整理得:3m-4n=10③,12m+4n=14④.将③+④得:15m=24,解得m=24/15.讲m=24/15代入③有,n=-26/20.则有x-2y=24/15,5x-3y=-26/20.解得x=﹣,y=.则方程组的解为.
二元一次方程(组)错解问题
知识讲解
方程(组)出现错解问题时,将解代入未错的那个,仍能满足方程。
例题精讲
二元一次方程(组)错解问题
例1.
甲、乙两人同求方程ax﹣by=7的整数解,甲正确地求出一个解为,乙把ax﹣by=7看成ax﹣by=1,求得一个解为,则a,b的值分别为( ).
A. B. C. D.
【答案】B
【解析】
题干解析:
首先根据题意把代入ax﹣by=7中得a+b=7,把代入ax﹣by=1中得:a﹣2b=1,组成方程组可解得a,b的值.
解:把代入ax﹣by=7中得:
a+b=7 ①,
把代入ax﹣by=1中得:
a﹣2b=1 ②,
把①②组成方程组得:,
解得:,
故选:B.
例2.
小明和小文同解一个二元一次方程组,小明把方程①抄错,求得的解为,小文把方程②抄错,求得的解为.你能根据提供的信息写出原方程组吗?
【答案】
见解析
【解析】
题干解析:解答此题的关键是把小明和小文得出的关于方程组的解代入相应正确的方程中,得到关于a、b的二元一次方程组,再求出a、b的值代入原方程组中即可.分别把代入方程②中,把代入方程①中,得到关于a、b的二元一次方程组,求出a、b的值即可.【解答】解:由题意,得,解得,故原方程组应为.
二元一次方程(组)同解问题
知识讲解
方程组同解时,可从两个方程组中随意抽取一个方程,组成一个新的方程组,新的方程组的解仍为原先的解。
?
例题精讲
二元一次方程(组)同解问题
例1.
已知方程组和有相同的解,则a,b的值为( ).
A. B. C. D.
【答案】D
【解析】
题干解析:
本题主要考查了二元一次方程的解及二元一次方程组的解法,正确理解题意,然后根据题意得到关于待定系数的方程组,解方程组是解答此题的关键.
因为方程组和有相同的解,所以把5x+y=3和x﹣2y=5联立解之求出x、y,再代入其他两个方程即可得到关于a、b的方程组,解方程组即可求解.
解:∵方程组和有相同的解,
∴方程组的解也它们的解,
解得:,
代入其他两个方程得,
解得:,故选D.
例2.
若方程组与的解相同,则a= ,b= .
【答案】
33,
【解析】
题干解析:解方程组得,代入方程组得,解得,故答案为:33,.
例3.
若关于x,y的方程组与有相同的解.
(1)求这个相同的解;
(2)求m,n的值.
【答案】
见解析
【解析】
题干解析:解:(1)联立得:,解得:;(2)把x=2,y=﹣1代入得:,解得:m=6,n=4.
当堂练习
单选题
练习1.
如果和都是某二元一次方程的解,则这个二元一次方程是( ).
A.x+2y=﹣3 B.2x﹣y=2
C.x﹣y=3 D.y=3x﹣5
练习2.
已知方程组:的解是:,则方程组:的解是( ).
A. B. C. D.
练习3.
若与|x﹣y﹣3|互为相反数,则x+y的值为( ).
A.3 B.9 C.12 D.27
练习4.
方程组的解为,则方程组的解为( ).
A. B. C. D.
练习5.
甲、乙两人同求方程ax﹣by=7的整数解,甲正确地求出一个解为,乙把ax﹣by=7看成ax﹣by=1,求得一个解为,则a,b的值分别为( ).
A. B. C. D.
练习6.
在,,,,,中,属于二元一次方程的有( ).
A.2个 B.3个 C.4个 D.5个
练习7.
已知3 =y是二元一次方程,那么k的值是( ).
A.2 B.3 C.1 D.0
练习8.
下列方程组中,是二元一次方程组的是( ).
A. B. C. D.
练习9.
二元一次方程组的解的情况是( ).
A.一个解 B.两个解 C.无数个解 D.无解
练习10.
已知关于x,y的二元一次方程组的解为,则a﹣2b的值是( ).
A.﹣2 B.2 C.3 D.﹣3
练习11.
方程ax-4y=x-1是二元一次方程,则a的取值为( ).
A.a≠0 B.a≠-1 C.a≠1 D.a≠2
练习12.
已知方程组中的x ,y相等,则n的值为( ).
A.1 B.3 C.-3 D.-4
填空题
练习1.
若方程组与的解相同,则a= ,b= .
练习2.
下列数对:①②③④⑤中,属于方程x+y=0的解有 ,属于x+y=2的解有 ,属于x﹣y=2的解有 .(只填序号)
练习3.
已知关于x、y的方程组的解为 ,那么关于x、y的二元一次方程组的解为___________。
练习4.
元旦期间,某服装商场按标价打折销售,小王去该商场买了两件衣服,第一件打6折,第二件打5折,共记230元,付款后,收银员发现两件衣服的标价牌换错了,又找给小王20元,请问两件衣服的原标价各是多少? 解:设第一件衣服的原标价为x元,第二件衣服的原标价为y元;由题意可得方程组__________。
练习5.
商店里把塑料凳整齐地叠放在一起,据图的信息,当有10张塑料凳整齐地叠放在一起时的高度是______cm.
解答题
练习1.
解方程组:
练习2.
解方程组:
单选题:CCDCB ACAAB CD
填空题:33, ③,①②,②③ 50
解答题
练习1:【答案】
见解析
【解析】
题干解析:解:②×4得:4x-4y=16③①+③得:7x = 35解得:x = 5把x = 5代入②得,y = 1∴原方程组的解为。
练习2:【答案】
见解析
【解析】
题干解析:解:方程组整理得:,①+②得:8x=24,解得:x=3,把x=3代入②得:y=﹣5,则方程组的解为。
