6.1菱形的性质与判定(第1课时)课件(27张PPT)
文档属性
| 名称 | 6.1菱形的性质与判定(第1课时)课件(27张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 1.1MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 鲁教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-02-15 16:23:40 | ||
图片预览





文档简介
(共28张PPT)
6.1 菱形的性质与判定
第六章 特殊平行四边形
第1课时 菱形的性质
1.了解菱形的概念.
2.探索并证明菱形的性质定理.
3.应用菱形的性质定理解决相关问题.
学习目标
问题:什么样的四边形是平行四边形?它有哪些性质呢?
平行四边形的性质:
边:对边平行且相等.
对角线:相交并相互平分.
角:对角相等,邻角互补.
复习回顾
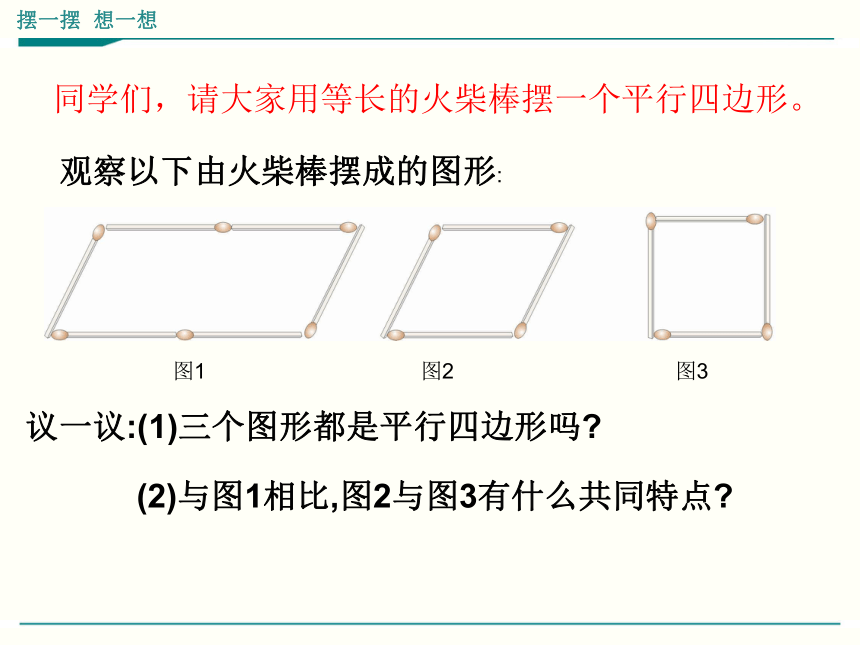
观察以下由火柴棒摆成的图形:
议一议:(1)三个图形都是平行四边形吗?
(2)与图1相比,图2与图3有什么共同特点?
摆一摆 想一想
同学们,请大家用等长的火柴棒摆一个平行四边形。
图1
图2
图3
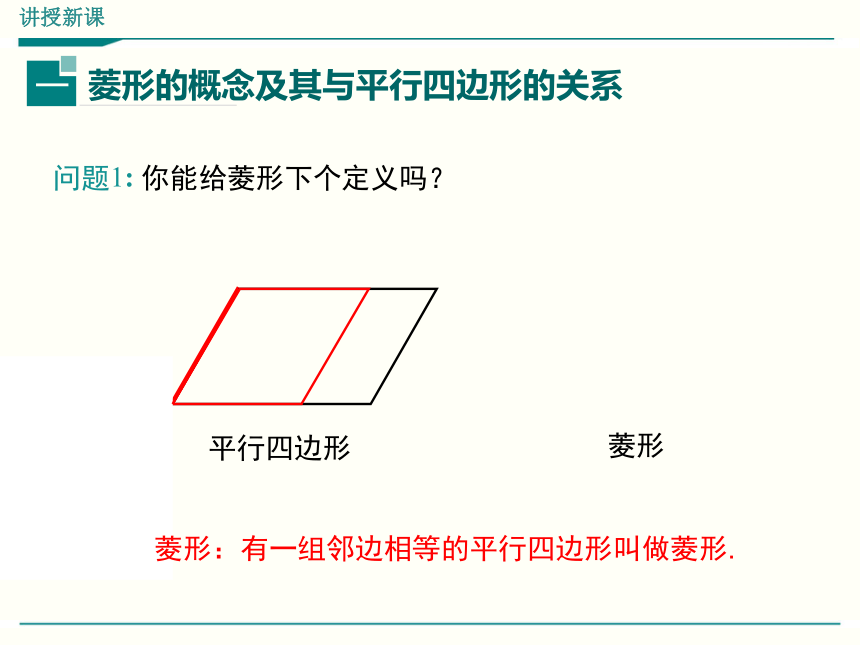
问题1: 你能给菱形下个定义吗?
平行四边形
菱形
菱形:有一组邻边相等的平行四边形叫做菱形.
讲授新课
菱形具有工整,匀称,美观等许多优点,常被人们用在图案设计上.
图片欣赏
2000多年前……
一把埋藏在地下2000多年前的古剑,出土时依然寒气逼人,毫无锈蚀,锋利无比,稍一用力,便可将多层白纸划破,剑身上整齐排列着黑色菱形暗花纹——越王勾践剑
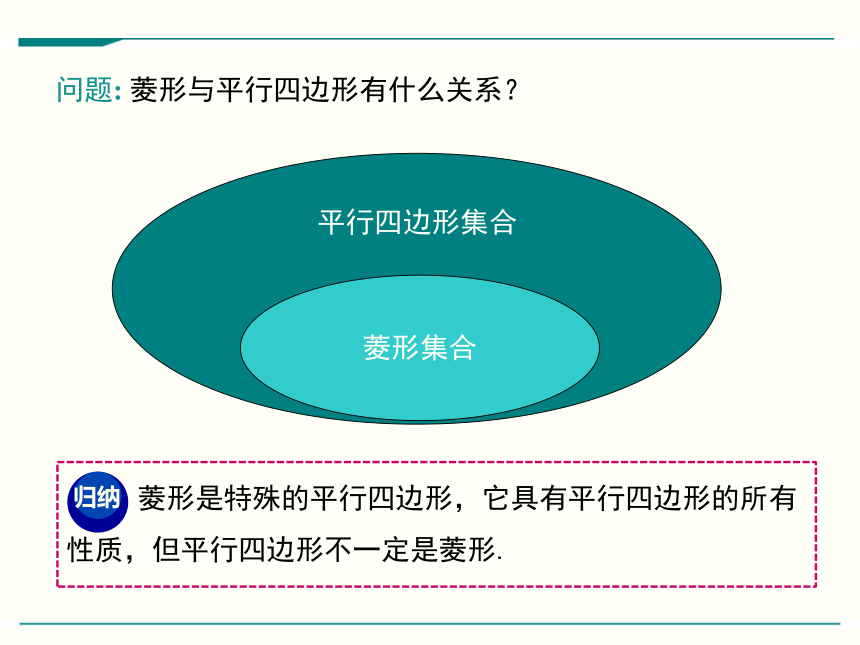
菱形是特殊的平行四边形,它具有平行四边形的所有性质,但平行四边形不一定是菱形.
问题: 菱形与平行四边形有什么关系?
平行四边形
菱形集合
平行四边形集合
做一做
请同学们用菱形纸片折一折,回答下列问题:
(1)菱形是轴对称图形吗?如果是,它有几条对称 轴?对称轴之间有什么位置关系?
(2)菱形中有哪些相等的线段?
1.菱形是轴对称图形,有两条对称轴(对称轴直线AC和直线BD).
2.菱形四条边都相等(AB=BC=CD=AD).
3.菱形的对角线互相垂直(AC⊥BD).
A
B
C
O
D
发现菱形的性质
已知:如图,在菱形ABCD中,AB=AD,对角线AC与BD相交 于点O.
求证:(1)AB = BC = CD =AD;
(2)AC⊥BD.
证明菱形的性质
证明:(1)∵四边形ABCD是菱形,
∴AB = CD,AD = BC(菱形的对边相等).
又∵AB=AD;
∴AB = BC = CD =AD.
求证:菱形的四条边相等,对角线互相垂直.
AC平分∠BAD和∠BCD, BD平分∠ABC和∠ADC.
(2)∵AB=AD,
∴△ABD是等腰三角形.
又∵四边形ABCD是菱形,
∴OB=OD.
在等腰三角形ABD中,
∵OB=OD,
∴AO⊥BD,
即AC⊥BD.
思考:菱形的一条对角线所分成的两个内角有什么关系?
∵四边形ABCD是菱形
∴AB=BC=CD=DA
∵四边形ABCD是菱形
∴AC⊥BC
菱形是特殊的平行四边形,它除具有平行四边形的所有性质外,还有平行四边形所没有的特殊性质.
对称性:是轴对称图形.
边:四条边都相等.
对角线:互相垂直.
角:对角相等,邻角互补.
边:对边平行且相等.
对角线:相交并相互平分.
菱形的特殊性质
平行四边形的性质
总结归纳
1.如图,在菱形ABCD中,两条对角线
AC与BD相交于点O,图中的等腰三角
形有______________________________,
直角三角形有_____________________________ ,而且它们是________(“全等”或“不全等”).
口答:
2.菱形具有而平行四边形不一定具有的性质是( )
A.内角和为360°
B.对角线互相垂直
C.对边平行
D.对角线互相平分
△ABD, △BCD,△ABC,△ADC
△ABO,△ADO,△BCO,△CDO
全等
B
例1:已知菱形ABCD中,对角线AC、BD相交于点O,AB=5cm,BD=8cm.
则:(1)BO=____________;
(2)AC=_____________.
典例精析
B
A
C
D
O
4cm
6cm
菱形中已知边长或对角线,求相关长度问题,一般利用菱形的对角线垂直平分,再结合勾股定理解题.
例2:如图,在菱形ABCD中,对角线AC与BD相交于点O,∠BAD=60°,BD =2,求菱形的边长AB和对角线AC的长.
解:∵四边形ABCD是菱形,
∴AC⊥BD(菱形的对角线互相垂直)
OB=OD= BD = ×2=1(菱形的对角线互相平分)
在等腰三角形ABD中,
∵∠BAD=60°,
∴△ABD是等边三角形.
∴AB = BD = 2.
典例精析
在RtΔAOB中,由勾股定理,得
OA2+OB2=AB2,
∴OA = =
∴AC=2OA= (菱形的对角线相互平分).
若菱形有一个内角为60°,那么60°角的两边与较
短的对角线可构成等边三角形,且两条对角线把菱形分成
四个全等的含30°角的直角三角形.
2
当堂练习
1.菱形具有而一般平行四边形不具有的性质是 ( ) A.对角相等 B.对边相等
C.是轴对称图形 D.对角线相等
2.如图,菱形的两条对角线长分别是6和8,则此菱形的周长是 ( )
A.40 B.32 C.24 D.20
C
D
3.在菱形ABCD中,AE⊥BC,AF⊥CD,E、F分别为BC,CD的中点,那么∠EAF的度数是 ( )
A.75° B.60° C.45° D.30°
B
6.已知菱形的一条对角线与边长相等,则菱形的四个内角度数分别为_____________________.
4.已知菱形的周长是12cm,那么它的边长是______.
5.菱形ABCD中∠ABC=120 °,则∠BAC=_______.
3cm
30°
60°、120°、60°、120°
7.已知:如图,四边形ABCD是菱形,F是AB上一点,DF交AC于E. 求证:∠AFD=∠CBE.
证明:∵四边形ABCD是菱形,
∴CB=CD, CA平分∠BCD.
∴∠BCE=∠DCE.
又 CE=CE,
∴△BCE≌△DCE(SAS).
∴∠CBE=∠CDE.
∵在菱形ABCD中,AB∥CD,
∴∠AFD=∠FDC.
∴∠AFD=∠CBE.
?
课堂小结
菱形的性质
菱形的性质
1.四边相等,对边平行
2.对角相等、邻角互补
3..对角线互相垂直平分,且每条对角线平分一组对角.
菱形的定义
有一组邻边相等的平行四边形是菱形.
1、已知菱形的周长为40cm,两对角线的长度之比为3:4,则两对角线的长分别为( )
A.6cm,8cm B.3cm,4cm
C.12cm,16cm D.24cm,32cm
2、已知菱形的一条对角线与边长相等,则菱形的邻角度数分别为 ( )
A. 45°,135° B. 60°,120°
C. 90°,90° D. 30°,150°
3、菱形的边长是13 cm,一条对角线的长是10 cm,则另一条对角线的长是( )
A.4cm B.24cm C.12cm D.22cm
B
B
C
4.菱形ABCD两组对边的距离AE,AF相等吗?为什么?
方法一:证明△ABE≌△ADF
方法二:等积法
∵ AE?BC=AF?CD
BC=CD
∴AE=AF
谢谢!
6.1 菱形的性质与判定
第六章 特殊平行四边形
第1课时 菱形的性质
1.了解菱形的概念.
2.探索并证明菱形的性质定理.
3.应用菱形的性质定理解决相关问题.
学习目标
问题:什么样的四边形是平行四边形?它有哪些性质呢?
平行四边形的性质:
边:对边平行且相等.
对角线:相交并相互平分.
角:对角相等,邻角互补.
复习回顾
观察以下由火柴棒摆成的图形:
议一议:(1)三个图形都是平行四边形吗?
(2)与图1相比,图2与图3有什么共同特点?
摆一摆 想一想
同学们,请大家用等长的火柴棒摆一个平行四边形。
图1
图2
图3
问题1: 你能给菱形下个定义吗?
平行四边形
菱形
菱形:有一组邻边相等的平行四边形叫做菱形.
讲授新课
菱形具有工整,匀称,美观等许多优点,常被人们用在图案设计上.
图片欣赏
2000多年前……
一把埋藏在地下2000多年前的古剑,出土时依然寒气逼人,毫无锈蚀,锋利无比,稍一用力,便可将多层白纸划破,剑身上整齐排列着黑色菱形暗花纹——越王勾践剑
菱形是特殊的平行四边形,它具有平行四边形的所有性质,但平行四边形不一定是菱形.
问题: 菱形与平行四边形有什么关系?
平行四边形
菱形集合
平行四边形集合
做一做
请同学们用菱形纸片折一折,回答下列问题:
(1)菱形是轴对称图形吗?如果是,它有几条对称 轴?对称轴之间有什么位置关系?
(2)菱形中有哪些相等的线段?
1.菱形是轴对称图形,有两条对称轴(对称轴直线AC和直线BD).
2.菱形四条边都相等(AB=BC=CD=AD).
3.菱形的对角线互相垂直(AC⊥BD).
A
B
C
O
D
发现菱形的性质
已知:如图,在菱形ABCD中,AB=AD,对角线AC与BD相交 于点O.
求证:(1)AB = BC = CD =AD;
(2)AC⊥BD.
证明菱形的性质
证明:(1)∵四边形ABCD是菱形,
∴AB = CD,AD = BC(菱形的对边相等).
又∵AB=AD;
∴AB = BC = CD =AD.
求证:菱形的四条边相等,对角线互相垂直.
AC平分∠BAD和∠BCD, BD平分∠ABC和∠ADC.
(2)∵AB=AD,
∴△ABD是等腰三角形.
又∵四边形ABCD是菱形,
∴OB=OD.
在等腰三角形ABD中,
∵OB=OD,
∴AO⊥BD,
即AC⊥BD.
思考:菱形的一条对角线所分成的两个内角有什么关系?
∵四边形ABCD是菱形
∴AB=BC=CD=DA
∵四边形ABCD是菱形
∴AC⊥BC
菱形是特殊的平行四边形,它除具有平行四边形的所有性质外,还有平行四边形所没有的特殊性质.
对称性:是轴对称图形.
边:四条边都相等.
对角线:互相垂直.
角:对角相等,邻角互补.
边:对边平行且相等.
对角线:相交并相互平分.
菱形的特殊性质
平行四边形的性质
总结归纳
1.如图,在菱形ABCD中,两条对角线
AC与BD相交于点O,图中的等腰三角
形有______________________________,
直角三角形有_____________________________ ,而且它们是________(“全等”或“不全等”).
口答:
2.菱形具有而平行四边形不一定具有的性质是( )
A.内角和为360°
B.对角线互相垂直
C.对边平行
D.对角线互相平分
△ABD, △BCD,△ABC,△ADC
△ABO,△ADO,△BCO,△CDO
全等
B
例1:已知菱形ABCD中,对角线AC、BD相交于点O,AB=5cm,BD=8cm.
则:(1)BO=____________;
(2)AC=_____________.
典例精析
B
A
C
D
O
4cm
6cm
菱形中已知边长或对角线,求相关长度问题,一般利用菱形的对角线垂直平分,再结合勾股定理解题.
例2:如图,在菱形ABCD中,对角线AC与BD相交于点O,∠BAD=60°,BD =2,求菱形的边长AB和对角线AC的长.
解:∵四边形ABCD是菱形,
∴AC⊥BD(菱形的对角线互相垂直)
OB=OD= BD = ×2=1(菱形的对角线互相平分)
在等腰三角形ABD中,
∵∠BAD=60°,
∴△ABD是等边三角形.
∴AB = BD = 2.
典例精析
在RtΔAOB中,由勾股定理,得
OA2+OB2=AB2,
∴OA = =
∴AC=2OA= (菱形的对角线相互平分).
若菱形有一个内角为60°,那么60°角的两边与较
短的对角线可构成等边三角形,且两条对角线把菱形分成
四个全等的含30°角的直角三角形.
2
当堂练习
1.菱形具有而一般平行四边形不具有的性质是 ( ) A.对角相等 B.对边相等
C.是轴对称图形 D.对角线相等
2.如图,菱形的两条对角线长分别是6和8,则此菱形的周长是 ( )
A.40 B.32 C.24 D.20
C
D
3.在菱形ABCD中,AE⊥BC,AF⊥CD,E、F分别为BC,CD的中点,那么∠EAF的度数是 ( )
A.75° B.60° C.45° D.30°
B
6.已知菱形的一条对角线与边长相等,则菱形的四个内角度数分别为_____________________.
4.已知菱形的周长是12cm,那么它的边长是______.
5.菱形ABCD中∠ABC=120 °,则∠BAC=_______.
3cm
30°
60°、120°、60°、120°
7.已知:如图,四边形ABCD是菱形,F是AB上一点,DF交AC于E. 求证:∠AFD=∠CBE.
证明:∵四边形ABCD是菱形,
∴CB=CD, CA平分∠BCD.
∴∠BCE=∠DCE.
又 CE=CE,
∴△BCE≌△DCE(SAS).
∴∠CBE=∠CDE.
∵在菱形ABCD中,AB∥CD,
∴∠AFD=∠FDC.
∴∠AFD=∠CBE.
?
课堂小结
菱形的性质
菱形的性质
1.四边相等,对边平行
2.对角相等、邻角互补
3..对角线互相垂直平分,且每条对角线平分一组对角.
菱形的定义
有一组邻边相等的平行四边形是菱形.
1、已知菱形的周长为40cm,两对角线的长度之比为3:4,则两对角线的长分别为( )
A.6cm,8cm B.3cm,4cm
C.12cm,16cm D.24cm,32cm
2、已知菱形的一条对角线与边长相等,则菱形的邻角度数分别为 ( )
A. 45°,135° B. 60°,120°
C. 90°,90° D. 30°,150°
3、菱形的边长是13 cm,一条对角线的长是10 cm,则另一条对角线的长是( )
A.4cm B.24cm C.12cm D.22cm
B
B
C
4.菱形ABCD两组对边的距离AE,AF相等吗?为什么?
方法一:证明△ABE≌△ADF
方法二:等积法
∵ AE?BC=AF?CD
BC=CD
∴AE=AF
谢谢!
