北师大版九年级数学上册第四章图形的相似回顾与思考的教案
文档属性
| 名称 | 北师大版九年级数学上册第四章图形的相似回顾与思考的教案 |

|
|
| 格式 | zip | ||
| 文件大小 | 116.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-02-15 00:00:00 | ||
图片预览


文档简介
《图形的相似》回顾与思考(1)
1、 教学目标
1、 知识技能
(1) 了解本章所学的主要内容,建立本章的知识体系;
(2) 正确合理地选择适当的判定方法找到相似三角形,运用相似三角形解决数学问题;
2、 数学思考
(1) 经历观察、实验、猜想、证明等找相似的过程,进一步发展几何直觉,发展合情推理能力和初步的演绎推理能力;
(2) 能有条理地、清晰地阐述自己的学习体验和结果,发展表达能力;
3、 问题解决
(1) 能与同学交流“找相似”的体验和结果,体验“交流”对自己的帮助;
(2) 在“找相似”的过程中形成反思意识,获得“找相似”的基本体验;
4、 情感态度
(1) 能积极参与到课堂学习活动中,对复习课有兴趣和热情;
(2) 体验数学活动充满着探索与创造,感受数学的严谨性;
(3) 形成实事求是的态度以及进行质疑和独立思考的习惯.
2、 教学重难点
1、 正确选择合适的模型和判定方法找到相似三角形,反思总结“找相似”的基本策略;
2、 从直观发现到自然说理的过渡.
3、 教学方法
在教师的组织和引导下,学生展示思维导图,采用独立思考和小组合作探究相结合,小组交流和全班交流相结合的方式.
4、 教学过程
(1) 建立体系,思维展示
学生课下独立总结,绘制思维导图,提前准备好同大家讲解.
(设计意图:帮助孩子们主动思考,培养他们反思总结及语言表达能力,以学生讲解展示的形式开启课堂,烘托课堂气氛)
(2) 牛刀小试,模型重现
1.如图,已知CA=6,CB=4 , AB=5,CD=2.若CE=3,则DE= .
2.如图,∠ABC=90?,BD⊥AC于D,DC=4 ,AD=9,则BD的长为 .
3.如图,F、C、D共线,BD⊥FD, EF⊥FD ,BC⊥EC ,若DC=2 ,BD=3,FC=6,EF的长为 .
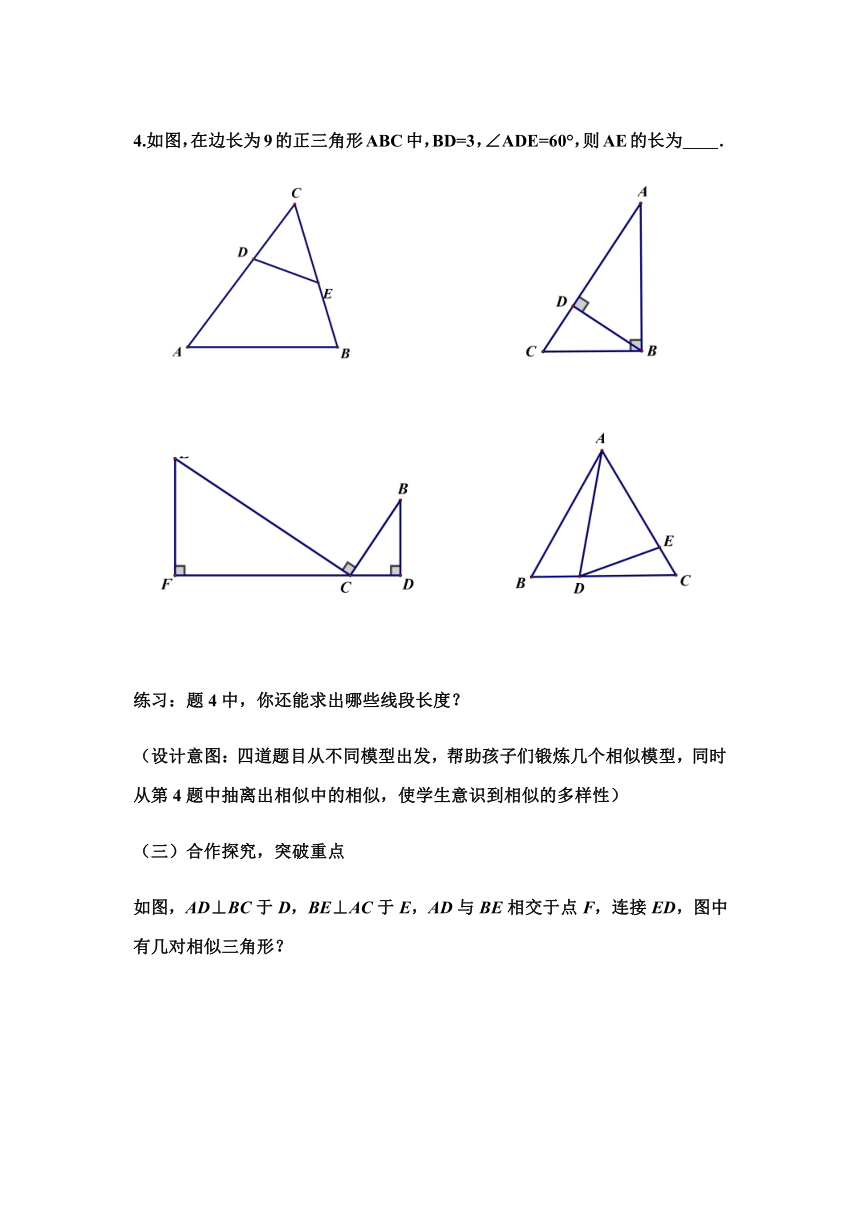
4.如图,在边长为9的正三角形ABC中,BD=3,∠ADE=60°,则AE的长为 .
练习:题4中,你还能求出哪些线段长度?
(设计意图:四道题目从不同模型出发,帮助孩子们锻炼几个相似模型,同时从第4题中抽离出相似中的相似,使学生意识到相似的多样性)
(三)合作探究,突破重点
如图,AD⊥BC于D,BE⊥AC于E,AD与BE相交于点F,连接ED,图中有几对相似三角形?
(设计意图:本题抽自学生已经做过的一道作业题,仅仅从找相似的角度让学生寻找并加以讨论,调动学生多个感官,其中多个相似的模型又一次提醒他们找相似的过程中寻找常见模型尤为重要;其中难度稍加提升的就是利用相似找相似类的二次相似,通过交流、讨论以及证明过程的板书体现证明中可能出现的问题,从问题中进行反思总结找到比较简单的证明相似的方法;利用动画分离相似的过程使学生再次获得直观的感受相似模型的多样性.)
(四)我有好题,与你分享
1.(1)如图1,已知DB⊥BC,AC⊥BC,垂足分别为点B,C,AE⊥CD于点F,求证:=.
(2)如图2,在△ABC中,点D在AB上,点E在BC上,且AE⊥CD于F点.若∠ACB=90°,=,且AE=2CD,求的值.
2.如图,△ABC是等腰三角形,AB=AC,AD⊥BC,取AC、AD的中点F、E,连接BE,作DG⊥BE,连接FG。
求证:FD=FG
3. 如图,已知四边形ABCD为矩形,AB等于16,BC等于12.点E在射线BC上,点F在线段BD上,且∠DEF=∠ADB,设BE=x,当△DEF为等腰三角形时求x的值。
4. (2019安徽T23)已知△ABC为等腰直角三角形,∠APB=∠BPC=135°,证明PA=2PC; 。
(设计意图:课堂的主体是学生,由学生展开,也回归于学生.因此,本环节交予四位小组长全权发挥,寻找经典好题与大家共享,由于课堂时间有限,民主选举一位小组长与大家分享总结,课下提前指导各位组长如何讲解,通过组长组织讲解的形式将课堂最主要核心的部分交予他们,让他们在交流中成长,在思考中收获,也极大程度的提高了学生学习的积极性.)
(五)小结反思,思想升华
我熟练掌握相关知识点了吗?
我领会了什么数学思想或方法?
我积累了哪些基本相似图形?
我还有什么疑惑?怎么办?
学生思考并进行交流补充,老师总结寄语.
(设计意图:以学生为主体,从知识与思想方面逐步深入进行总结,升华了本节课主要思想,体现新课标下学生的主体地位,使学生在交流中锻炼语言表达的能力,主动思考本节课的主要模型,教师从历史中的相似三角形入手带大家感受数学大家的智慧,为本节课画上一个圆满的句号.)
5、 教学反思
本节课的教学设计力求以学生为主体,从课前准备到课堂讲解以及习题的分享都交予学生,在课堂结构上,层次分明,环环相扣;四道练习题的设计,目标明确,层层递进;在引导方式上,指向清晰,适时讨论.课堂充分利用多媒体资源,设计动画,帮助学生直观感知,突破重点,利用几何画板动态演示,解决动点问题,也是学生在清晰的思路中分析试题,帮助他们解决复杂问题.
图2
图1
同课章节目录
- 第一章 特殊平行四边形
- 1 菱形的性质与判定
- 2 矩形的性质与判定
- 3 正方形的性质与判定
- 第二章 一元二次方程
- 1 认识一元二次方程
- 2 用配方法求解一元二次方程
- 3 用公式法求解一元二次方程
- 4 用因式分解法求解一元二次方程
- 5 一元二次方程的根与系数的关系
- 6 应用一元二次方程
- 第三章 概率的进一步认识
- 1 用树状图或表格求概率
- 2 用频率估计概率
- 第四章 图形的相似
- 1 成比例线段
- 2 平行线分线段成比例
- 3 相似多边形
- 4 探索三角形相似的条件
- 5 相似三角形判定定理的证明
- 6 利用相似三角形测高
- 7 相似三角形的性质
- 8 图形的位似
- 第五章 投影与视图
- 1 投影
- 2 视图
- 第六章 反比例函数
- 1 反比例函数
- 2 反比例函数的图象与性质
- 3 反比例函数的应用
