湘教版七年级数学下册第2章 整式的乘法单元总结提升课件(20张)
文档属性
| 名称 | 湘教版七年级数学下册第2章 整式的乘法单元总结提升课件(20张) |

|
|
| 格式 | zip | ||
| 文件大小 | 526.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 湘教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-02-16 00:00:00 | ||
图片预览







文档简介
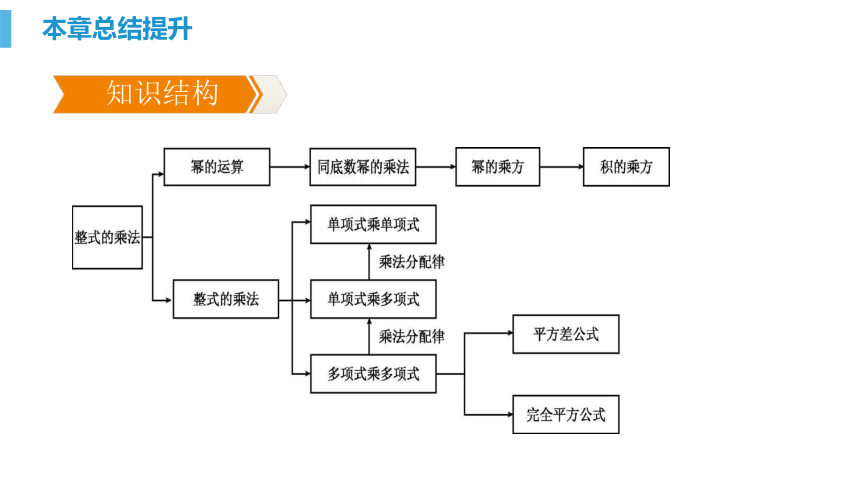
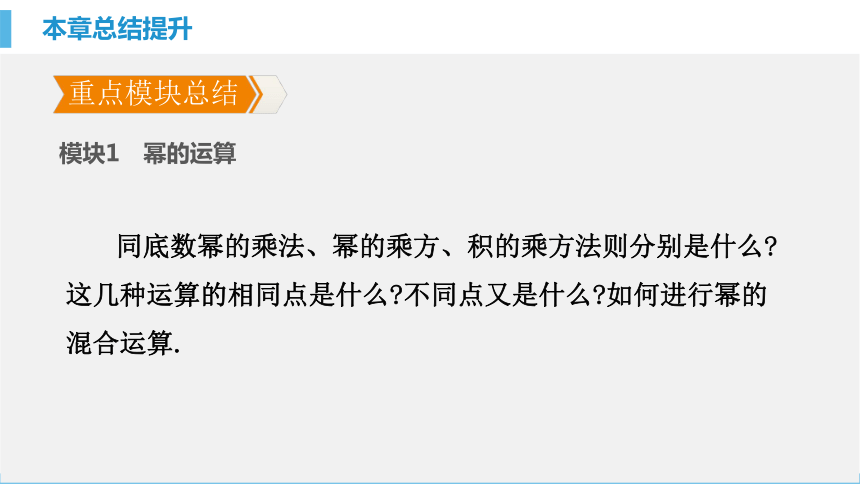
课件20张PPT。总结提升 知识结构关系重点模块总结重点模块总结综合能力提升 知识结构关系本章总结提升重点模块总结模块1 直角三角形的性质直角三角形是特殊的三角形,它的特殊性体现在哪里?其中揭示线段倍分关系的是哪个性质?模块1 幂的运算 同底数幂的乘法、幂的乘方、积的乘方法则分别是什么?这几种运算的相同点是什么?不同点又是什么?如何进行幂的混合运算.本章总结提升本章总结提升本章总结提升【归纳总结】幂的运算技巧
(1)进行幂的混合运算时,应先算幂的乘方,积的乘方,再算同底数幂相乘,然后合并同类项.
(2)幂的运算法则可以正用,也可以逆用.当出现指数相加时,需要逆用同底数幂相乘法则;当出现指数相乘时,需要逆用幂的乘方法则.
模块2 整式乘法与乘法公式 整式的乘法有哪几种形式?多项式乘多项式与单项式乘多项式有什么关系?它们的运算法则有什么不同?完全平方公式有哪两种形式?平方差公式与完全平方公式有什么不同?本章总结提升本章总结提升本章总结提升【归纳总结】整式的乘法
整式乘法与乘法公式是解方程、化简求值的基础,一般思路是将多项式乘多项式转化为多项式乘单项式,再进一步转化为单项式乘单项式.能使用乘法公式时优先使用乘法公式计算.若是混合运算,运算顺序仍然是先乘方,再乘法,如有同类项要合并,结果要化为最简形式.本章总结提升模块3 代数式的化简求值 什么叫做代数式的值?求代数式的值的常用方法有哪些?解决整式的化简与求值问题的一般步骤有哪些?本章总结提升本章总结提升【归纳总结】利用整式运算化简求值
求代数式的值时,一般情况是先化简,再把字母的值代入化简后的式子中求值.化简的过程就是整式运算的过程,解答过程中,要灵活运用幂的运算性质、整式的运算法则及乘法公式.本章总结提升模块4 整体思想的运用 整体思想在数学解题中的作用是什么?如何发现问题的整体结构特征?整体思想的运用方法有哪些?本章总结提升本章总结提升【归纳总结】整体思想在整式乘法中的应用
整体思想是一种重要的数学思想,在解题中有着广泛的应用.使用整体思想的关键是善于用“集成”的眼光,把某些式子或图形看成一个整体,把握它们之间的关联,进行有目的、有意识的整体处理.在解题过程中,将已知条件或求值的式子视为一个整体,使其保持相对的稳定,通过整体代入或整体变形,简化解答过程,减小计算量.本章总结提升综合能力提升本章总结提升本章总结提升本章总结提升
谢 谢 观 看!
(1)进行幂的混合运算时,应先算幂的乘方,积的乘方,再算同底数幂相乘,然后合并同类项.
(2)幂的运算法则可以正用,也可以逆用.当出现指数相加时,需要逆用同底数幂相乘法则;当出现指数相乘时,需要逆用幂的乘方法则.
模块2 整式乘法与乘法公式 整式的乘法有哪几种形式?多项式乘多项式与单项式乘多项式有什么关系?它们的运算法则有什么不同?完全平方公式有哪两种形式?平方差公式与完全平方公式有什么不同?本章总结提升本章总结提升本章总结提升【归纳总结】整式的乘法
整式乘法与乘法公式是解方程、化简求值的基础,一般思路是将多项式乘多项式转化为多项式乘单项式,再进一步转化为单项式乘单项式.能使用乘法公式时优先使用乘法公式计算.若是混合运算,运算顺序仍然是先乘方,再乘法,如有同类项要合并,结果要化为最简形式.本章总结提升模块3 代数式的化简求值 什么叫做代数式的值?求代数式的值的常用方法有哪些?解决整式的化简与求值问题的一般步骤有哪些?本章总结提升本章总结提升【归纳总结】利用整式运算化简求值
求代数式的值时,一般情况是先化简,再把字母的值代入化简后的式子中求值.化简的过程就是整式运算的过程,解答过程中,要灵活运用幂的运算性质、整式的运算法则及乘法公式.本章总结提升模块4 整体思想的运用 整体思想在数学解题中的作用是什么?如何发现问题的整体结构特征?整体思想的运用方法有哪些?本章总结提升本章总结提升【归纳总结】整体思想在整式乘法中的应用
整体思想是一种重要的数学思想,在解题中有着广泛的应用.使用整体思想的关键是善于用“集成”的眼光,把某些式子或图形看成一个整体,把握它们之间的关联,进行有目的、有意识的整体处理.在解题过程中,将已知条件或求值的式子视为一个整体,使其保持相对的稳定,通过整体代入或整体变形,简化解答过程,减小计算量.本章总结提升综合能力提升本章总结提升本章总结提升本章总结提升
谢 谢 观 看!
