苏科版七年级数学下册 第7章 平面图形的认识(二) 单元测试卷(含答案)
文档属性
| 名称 | 苏科版七年级数学下册 第7章 平面图形的认识(二) 单元测试卷(含答案) |  | |
| 格式 | zip | ||
| 文件大小 | 778.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-02-15 17:10:21 | ||
图片预览


文档简介
第7章 平面图形的认识(二) 单元测试卷
一、单选题
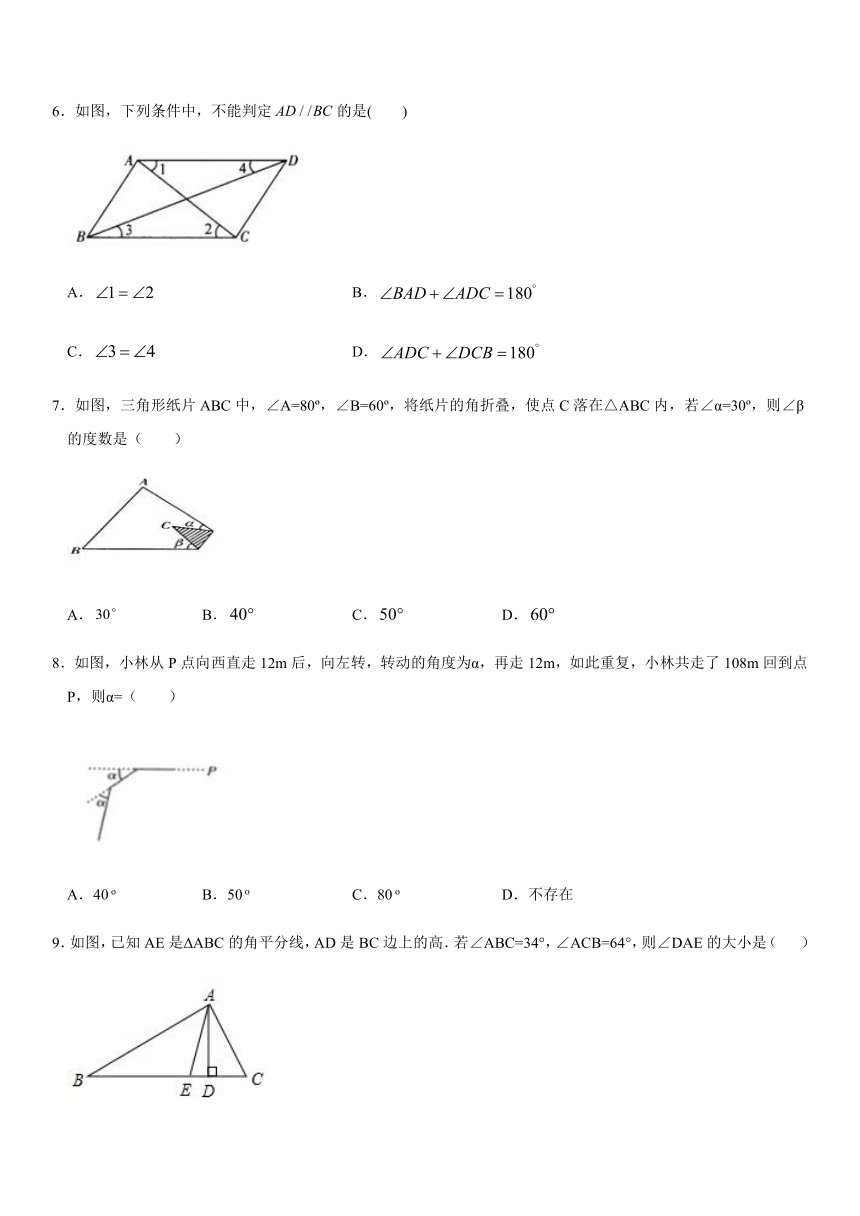
1.以下列各组线段长为边,不能组成三角形的是( )
A.8cm,7cm,13cm B.6cm,6cm,12cm C.5cm,5cm,2cm D.10cm,15cm,17cm
2.若一个多边形每一个内角都是135?,则这个多边形的边数是 ( )
A.6 B.8 C.10 D.12
3.如图,已知直线AB∥CD,∠GEB的平分线EF交CD于点F,∠1=42°,则∠2等于( )
A.138° B.142° C.148° D.159°
4.如图,∠A+∠B+∠C+∠D+∠E+∠F的度数为( )
A.180° B.360° C.270° D.540°
5.如图,△ABC中,∠ACB=90°,沿CD折叠△CBD,使点B恰好落在AC边上的点E处,若∠A=25°,则∠BDC等于( )
A.44° B.60° C.67° D.70°
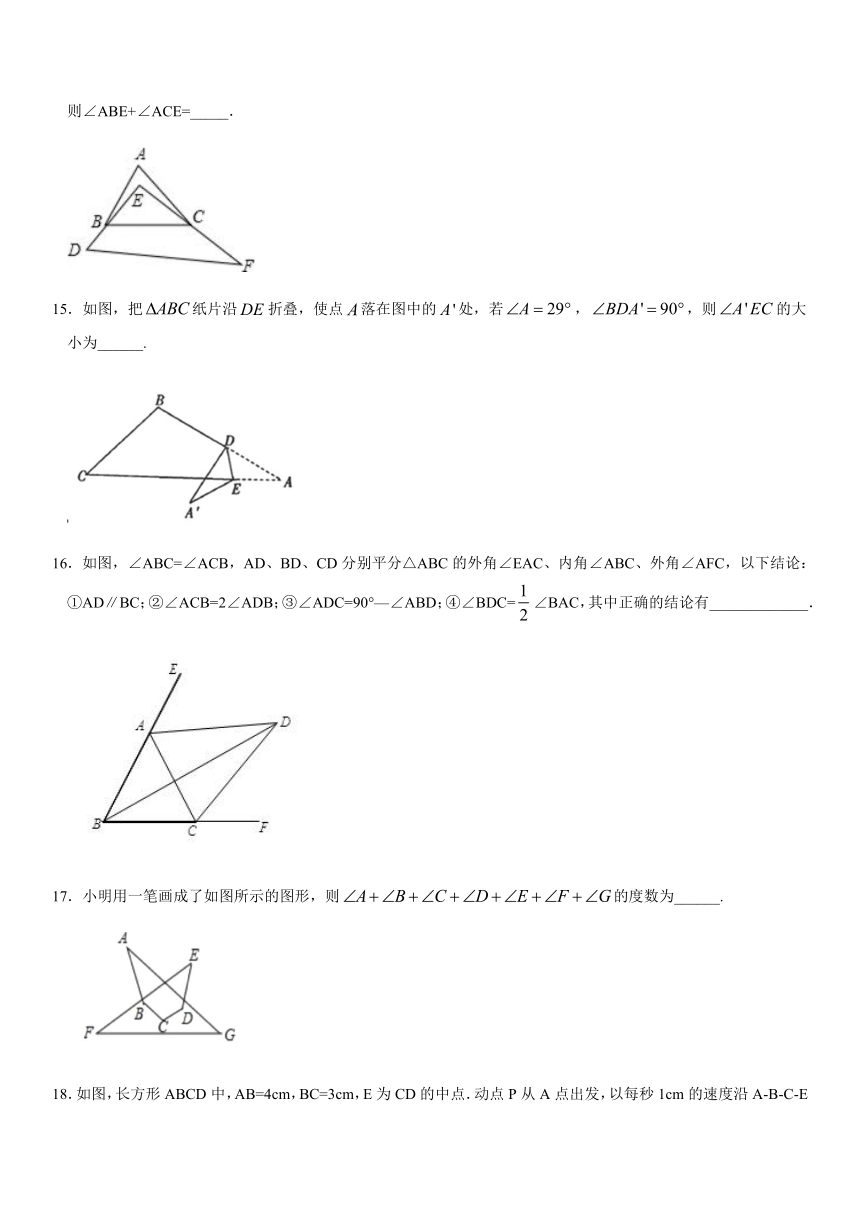
6.如图,下列条件中,不能判定的是( )
A. B.
C. D.
7.如图,三角形纸片ABC中,∠A=80?,∠B=60?,将纸片的角折叠,使点C落在△ABC内,若∠α=30?,则∠β的度数是( )
A. B. C. D.
8.如图,小林从P点向西直走12m后,向左转,转动的角度为α,再走12m,如此重复,小林共走了108m回到点P,则α=( )
A.40 o B.50 o C.80 o D.不存在
9.如图,已知AE是ΔABC的角平分线,AD是BC边上的高.若∠ABC=34°,∠ACB=64°,则∠DAE的大小是( )
A.5° B.13° C.15° D.20°
10.如图,在△ABC中,点D是BC边上的一点,E,F分别是AD,BE的中点,连结CE,CF,若S△CEF=5,则△ABC的面积为( )
A.15 B.20 C.25 D.30
二、填空题
11.一个三角形三个内角的度数之比为,则三角形按角分它的形状是_____三角形.
12.一个八边形从一个顶点出发有______条对角线.
13.已知:如图,直线AB、CD被直线GH所截,,求证: AB // CD. 完成下面的证明:
证明:∵AB被直线GH所截,
∴
∵
∴
∴ // ( )(填推理的依据).
14.将如图所示的一块直角三角板放置在△ABC上,使三角板的两条直角边DE、EF分别经过点B、C,若∠A=70°,则∠ABE+∠ACE=_____.
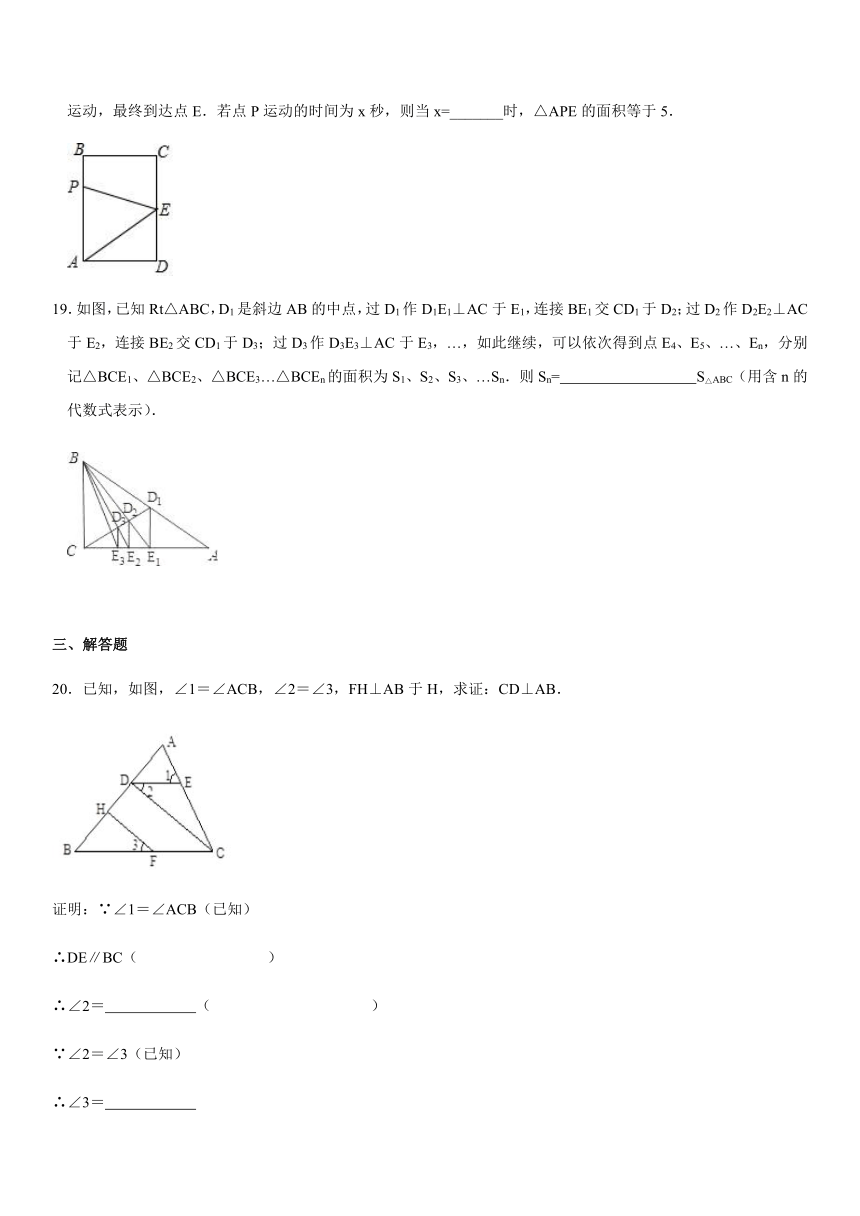
15.如图,把纸片沿折叠,使点落在图中的处,若,,则的大小为______.
16.如图,∠ABC=∠ACB,AD、BD、CD分别平分△ABC的外角∠EAC、内角∠ABC、外角∠AFC,以下结论:①AD∥BC;②∠ACB=2∠ADB;③∠ADC=90°—∠ABD;④∠BDC=∠BAC,其中正确的结论有_____________.
17.小明用一笔画成了如图所示的图形,则的度数为______.
18.如图,长方形ABCD中,AB=4cm,BC=3cm,E为CD的中点.动点P从A点出发,以每秒1cm的速度沿A-B-C-E运动,最终到达点E.若点P运动的时间为x秒,则当x=_______时,△APE的面积等于5.
19.如图,已知Rt△ABC,D1是斜边AB的中点,过D1作D1E1⊥AC于E1,连接BE1交CD1于D2;过D2作D2E2⊥AC于E2,连接BE2交CD1于D3;过D3作D3E3⊥AC于E3,…,如此继续,可以依次得到点E4、E5、…、En,分别记△BCE1、△BCE2、△BCE3…△BCEn的面积为S1、S2、S3、…Sn.则Sn= S△ABC(用含n的代数式表示).
三、解答题
20.已知,如图,∠1=∠ACB,∠2=∠3,FH⊥AB于H,求证:CD⊥AB.
证明:∵∠1=∠ACB(已知)
∴DE∥BC( )
∴∠2= ( )
∵∠2=∠3(已知)
∴∠3=
∴CD∥FH( )
∴∠BDC=∠BHF( )
又∵FH⊥AB(已知)
∴ ( )
∵CD∥FH
∴∠BHF=∠BDC=90°( )
即CD⊥AB( )
21.如图,为的高,为的角平分线,若,.
(1) ?;
(2)求的度数;
(3)若点为线段上任意一点,当为直角三角形时,则求的度数.
22.如图:已知AB∥CD,∠1=∠2,∠DFE=105°.求∠DBC的度数.
23.如图,已知,按要求作图.
(1)过点作的垂线段;
(2)过作、的垂线分别交于点、;
(3),,,,求点到线段的距离.
24.已知如图1,在中,是的角平分线,是边上的高,.
(1)求的度数.
(2)如图2,若点为延长线上一点,过点作于点,求的度数.
25.一个多边形的内角和是它的外角和的4倍,求:
(1)这个多边形是几边形?
(2)这个多边形共有多少条对角线?
26.将一副三角板中的两个直角顶点叠放在一起(如图①),其中,,.
(1)猜想与的数量关系,并说明理由;
(2)若,求的度数;
(3)若按住三角板不动,绕顶点转动三角,试探究等于多少度时,并简要说明理由.
27.提出问题:
(1)如图,我们将图(1)所示的凹四边形称为“镖形”.在“镖形”图中,∠AOC与∠A、∠C、∠P的数量关系为_______.
(2)如图(2),已知AP平分∠BAD,CP平分∠BCD,∠B =28°,∠D=48°.求∠P的度数.
由(1)结论得:∠AOC =∠PAO +∠PCO+∠P
所以2∠AOC=2∠PAO +2∠PCO+2∠P即2∠AOC =∠BAO +∠DCO+2∠P
因为∠AOC =∠BAO +∠B,∠AOC =∠DCO +∠D
所以2∠AOC=∠BAO +∠DCO+∠B +∠D
所以∠P=_______.
解决问题:
(3)如图(3),直线AP平分∠BAD,CP平分∠BCD的外角∠BCE,猜想∠P与∠B、∠D的数量关系是_______;
(4)如图(4),直线AP平分∠BAD的外角∠FAD,CP平分∠BCD的外角∠BCE,猜想∠P与∠B、∠D的数量关系是_______.
28.如图,AD∥BC,若∠ADP=∠α,∠BCP=∠P,射线OM上有一动点P.
(1)当点P在A,B两点之间运动时,∠CPD与∠α、∠β之间有何数量关系?请说明理由
(2)如果点P在A、B两点外侧运动时(点P与点A、B、O三点不重合),请你直接写出∠CPD与∠α、∠β之间的何数量关系.
参考答案
一、选择题
1.B 2.B 3.D 4.B 5.D
6.B 7.C 8.A 9.C 10.B
二、填空题
11.直角 12.5 13.∠3,180°,AB,CD,同旁内角互补,两直线平行.
14.20°. 15.32° 16.①②③④ 17.540°.
18.或5 19.
三、解答题
20.同位角相等,两直线平行;∠BCD,两直线平行,内错角相等;∠BCD;同位角相等,两直线平行;两直线平行,同位角相等;∠BHF=90°,垂直的定义;两直线平行,同位角相等;垂直的定义.
【分析】
先根据,∠1=∠ACB得出DE∥BC,故可得出∠2=∠BCD,根据∠2=∠3得出∠3=∠BCD,所以CD∥FH,再由垂直的定义得出∠BHF=90°由平行线的性质即可得出结论.
【详解】
∵∠1=∠ACB(已知),
∴DE∥BC(同位角相等,两直线平行),
∴∠2=∠BCD.(两直线平行,内错角相等).
∵∠2=∠3(已知),
∴∠3=∠BCD
∴CD∥FH(同位角相等,两直线平行),
∴∠BDC=∠BHF(两直线平行,同位角相等)
又∵FH⊥AB(已知),
∴∠BHF=90°(垂直的定义).
∵CD∥FH
∴∠BDC=∠BHF=90°,(两直线平行,同位角相等)
∴CD⊥AB(垂直的定义).
故答案为:同位角相等,两直线平行;∠BCD,两直线平行,内错角相等;∠BCD;同位角相等,两直线平行;两直线平行,同位角相等;∠BHF=90°;垂直的定义;两直线平行,同位角相等;垂直的定义.
21.(1)26;(2)12°;(3)∠BFG的度数为58°或18°.
【分析】
(1)根据BF是∠ABC的角平分线且,可求出∠ABD,又为的高即可得出答案;
(2)根据∠AFB和∠ABF即可求出∠BAC,又AE是∠BAC的角平分线可求出∠BAE的度数,通过∠DAE=∠BAE-∠BAD即可得出答案;
(3)为直角三角形需要分情况讨论:①∠FGC=90°;②∠GFC=90°,针对以上两种情况分别求解.
【详解】
(1)∵BF是∠ABC的角平分线且
∴∠ABF=32°∠ABD=64°
又为的高
∴∠BAD=90°-∠ABD=26°
(2)∵,∠ABF=32°
∴∠BAC=180°-∠ABF-∠AFB=76°
又∵AE是∠BAC的角平分线
∴∠BAE=∠CAE=38°
∴∠DAE=∠BAE-∠BAD=12°
(3)在△ABC中,∠C=40°
∠BFC=180°-∠BFA=108°
当∠FGC=90°时,为直角三角形,此时∠CFG=50°
∴∠BFG=∠BFC-∠CFG=58°
当∠GFC=90°时,为直角三角形
∴∠BFG=∠BFC-∠CFG=18°
综上,∠BFG的度数为58°或18°.
22.105°.
【分析】
由AB∥CD,根据两直线平行,内错角相等可得∠2=∠3,从而可得∠1=∠3,再根据同位角相等,两直线平行可得FE∥BC,再根据两直线平行,同位角相等即可求得答案.
【详解】
∵AB∥CD,
∴∠2=∠3,
又∵∠1=∠2,
∴∠1=∠3,
∴FE∥BC,
∴∠DBC=∠DFE=105°.
23.(1)详见解析;(2)详见解析;(3)点到线段的距离为.
【分析】
(1)、(2)根据几何语言作图;
(3)利用三角形面积公式得到,然后把,,代入计算可求出.
【详解】
解:(1)如图,为所作;
(2)如图,、为所作;
(3),
,
即点到线段的距离为.
24.(1)°;(2) .
【分析】
(1)根据求出,又因为是的角平分线可求出,再根据已知求出,根据三角形内角和公式即可求解;(2)根据,可证得,所以,则有.
【详解】
解:(1)在中,
,
平分
,
在中,
为三角形的高,
.
在中,
.
(2)
由(1)可知
.
25.(1)n=10;(2)35条.
【分析】
(1)根据多边形的内角和公式和外角和是360°列方程求解即可;
(2)根据多边形的对角线条数公式计算即可.
【详解】
解:(1)设这个多边形是n边形,则
(n﹣2)?180°=4×360°,
解得n=10,所以这个多边形是十边形.
(2)10×(10﹣3)÷2=35(条).
26.(1),理由详见解析;(2)135°;(3)等于或时,.
【分析】
(1)依据∠BCD=∠ACB+∠ACD=90°+∠ACD,即可得到∠BCD+∠ACE的度数;
(2)设∠ACE=,则∠BCD=3,依据∠BCD+∠ACE=180°,即可得到∠BCD的度数;
(3)分两种情况讨论,依据平行线的性质,即可得到当∠BCD等于150°或30°时,CE//4B.
【详解】
解:(1),理由如下:
,
;
(2)如图①,设,则,
由(1)可得,
,
,
;
(3)分两种情况:
①如图1所示,当时,,
又,
;
②如图2所示,当时,,
又,
.
综上所述,等于或时,.
27.(1)∠AOC=∠A+∠P+∠C;(2)38°;(3)∠P=90°+(∠B+∠D);(4)∠P=180°-(∠B+∠D).
【分析】
(1)延长CO,交AP与B,根据三角形外角性质即可得答案;(2)根据2∠AOC=∠BAO +∠DCO+2∠P,2∠AOC=∠BAO +∠DCO+∠B+∠D,可得2∠P=∠B+∠D,进而可得答案;(3)由角平分线的定义可得∠PAB=∠PAD,∠PCB=∠PCE,根可三角形内角和定理可得2∠PAB+∠B=180°-2∠PCB+∠D,由(1)可知∠P=∠PAB+∠B+∠PCB,利用等量代换即可得答案;(4)由角平分线的定义可得∠FAP=∠PAD,∠PCE=∠PCB,根据四边形的内角和等于360°可得(180°-∠FAP)+∠P+∠PCB+∠B=360°,∠PAD+∠P+(180°-∠PCE)+∠D=360°,然后整理即可得解;
【详解】
(1)如图,延长CO,交AP与B,
∵∠AOC=∠A+∠ABO,∠ABO=∠C+∠P,
∴∠AOC=∠A+∠P+∠C,
故答案为∠AOC=∠A+∠P+∠C,
(2)∵2∠AOC =∠BAO +∠DCO+2∠P,2∠AOC=∠BAO +∠DCO+∠B+∠D,
∴2∠P=∠B+∠D,
∴∠P=(28°+48°)=38°,
故答案为38°
(3)∵直线AP平分∠BAD,CP平分∠BCD的外角∠BCE,
∴∠PAB=∠PAD,∠PCB=∠PCE,
∴2∠PAB+∠B=180°-2∠PCB+∠D,
∴180°-2(∠PAB+∠PCB)+∠D=∠B
∵∠P=∠PAB+∠B+∠PCB,
∴∠PAB+∠PCB=∠P-∠B,
∴180°-2(∠P-∠B)+∠D=∠B,即∠P=90°+(∠B+∠D).
(4)∵直线AP平分∠BAD的外角∠FAD,CP平分∠BCD的外角∠BCE,
∴∠FAP=∠PAO,∠PCE=∠PCB,
在四边形APCB中,(180°-∠FAP)+∠P+∠PCB+∠B=360°①,
在四边形APCD中,∠PAD+∠P+(180°-∠PCE)+∠D=360°②,
①+②得:2∠P+∠B+∠D=360°,
∴∠P=180°-(∠B+∠D).
28.(1)∠CPD=∠α+∠β,理由见解析;(2)①当P在BA延长线时,∠CPD=∠β﹣∠α;理由见解析;②当P在BO之间时,∠CPD=∠α﹣∠β.理由见解析.
【分析】
(1)过P作PE∥AD交CD于E,根据平行线判定和性质,得∠CPD=∠α+∠β.(2)过P作PE∥AD交CD于E,根据平行线判定和性质,得①当P在BA延长线时,∠CPD=∠β﹣∠α;②当P在BO之间时,∠CPD=∠α﹣∠β.
【详解】
(1)∠CPD=∠α+∠β,理由如下:
如图1,过P作PE∥AD交CD于E,
∵AD∥BC,
∴AD∥PE∥BC,
∴∠α=∠DPE,∠β=∠CPE,
∴∠CPD=∠DPE+∠CPE=∠α+∠β;
(2)分两种情况:①当P在BA延长线时,∠CPD=∠β﹣∠α;
理由:如图2,过P作PE∥AD交CD于E,
∵AD∥BC,
∴AD∥PE∥BC,
∴∠α=∠DPE,∠β=∠CPE,
∴∠CPD=∠CPE﹣∠DPE=∠β﹣∠α;
②当P在BO之间时,∠CPD=∠α﹣∠β.
理由:如图3,过P作PE∥AD交CD于E,
∵AD∥BC,
∴AD∥PE∥BC,
∴∠α=∠DPE,∠β=∠CPE,
∴∠CPD=∠DPE﹣∠CPE=∠α﹣∠β.
同课章节目录
- 第7章 平面图形的认识(二)
- 7.1 探索直线平行的条件
- 7.2 探索平行线的性质
- 7.3 图形的平移
- 7.4 认识三角形
- 7.5 多边形的内角和与外角和
- 第8章 幂的运算
- 8.1 同底数幂的乘法
- 8.2 幂的乘方与积的乘方
- 8.3 同底数幂的除法
- 第9章 整式乘法与因式分解
- 9.1 单项式乘单项式
- 9.2 单项式乘多项式
- 9.3 多项式乘多项式
- 9.4 乘法公式
- 9.5 多项式的因式分解
- 第10章 二元一次方程组
- 10.1 二元一次方程
- 10.2 二元一次方程组
- 10.3 解二元一次方程组
- 10.4 三元一次方程组
- 10.5 用二元一次方程解决问题
- 第11章 一元一次不等式
- 11.1 生活中的不等式
- 11.2 不等式的解集
- 11.3 不等式的性质
- 11.4 解一元一次不等式
- 11.5 用一元一次不等式解决问题
- 11.6 一元一次不等式组
- 第12章 证明
- 12.1 定义与命题
- 12.2 证明
- 12.3 互逆命题
